一类半线性椭圆型方程组的边值问题

金启胜, 钟金标

(1.安庆师范大学,安庆职业技术学院,安徽 安庆 246003;2.安庆师范大学数学与计算科学学院,安徽 安庆 246133)

1 引言

考虑下面一类半线性椭圆型方程组:

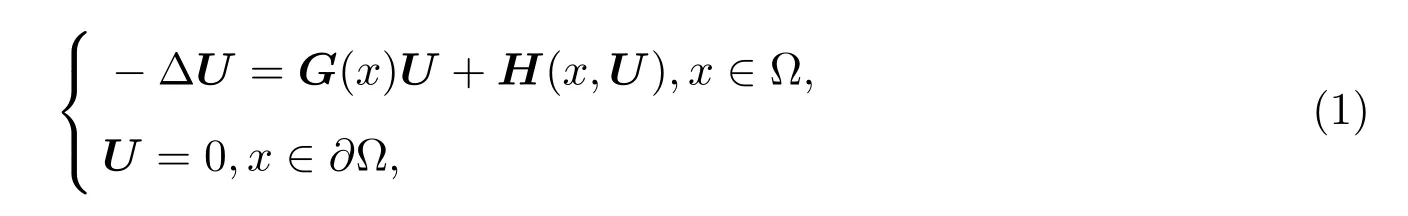
其中

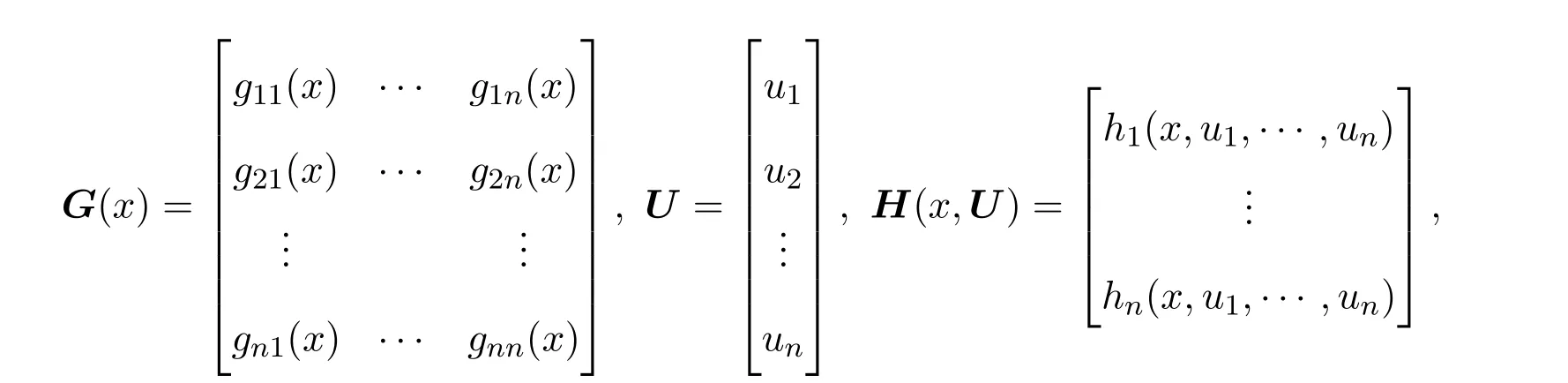
而且

(I)Ω⊂Rn是有界光滑域;

(II)G(x)中每一项在Ω上面连续,并且gij≥0,i,j=1,2,···,n;

(III)hk(x,u1,···,un),k=1,2,···,n对于每一个变元都连续;

(IV)存在正常数c,对于 (x,U)∈R2n,都有 0≤hk(x,U)≤c,x=1,2,···,n成立.

令

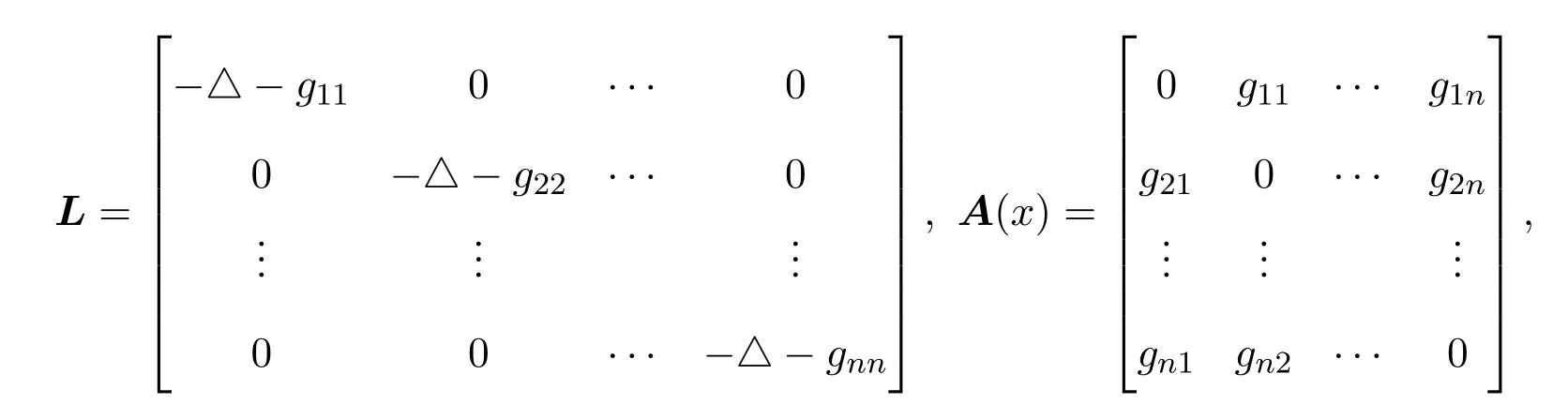
引进范数

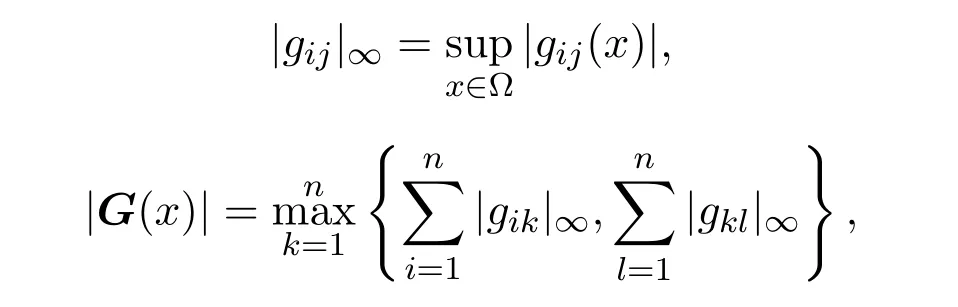
λ1为狄利克雷条件下−△在Ω的第一特征值.

所以方程组(1)和下面方程组(2)等价:

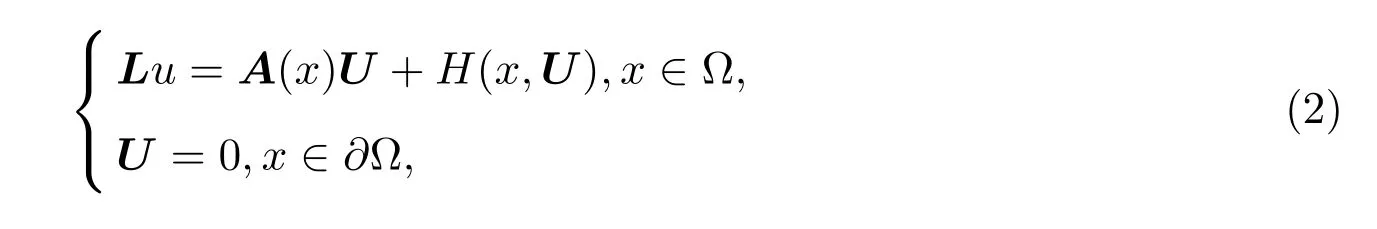
引理 1.1[1]设Z是一个Banach空间,C是Z的一个闭凸集.如果T是C到C的一个紧映射,R是一个正常数,使得对任意的U∈C,||U||=R.

但是UtT(U),0≤t≤1,那么T有一个不动点U∈C,而且||U||≤R.

2 主要结论和证明

定理 2.1[2]如果|G(x)|<λ1,那么方程组(3)只有零解.

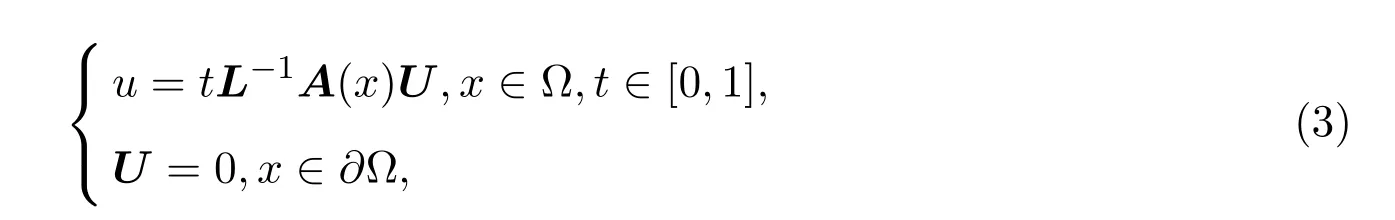
证明因为gkk<|G(x)|<λ1,所以gkk<λ1,k=1,2,···,n故算子L存在逆算子

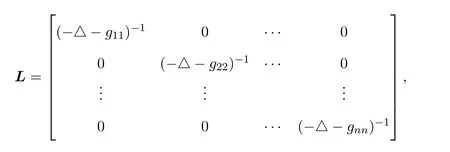
并且

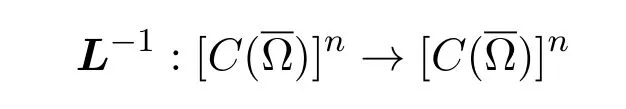
是线性紧正算子[3].故方程组(3)等价于:

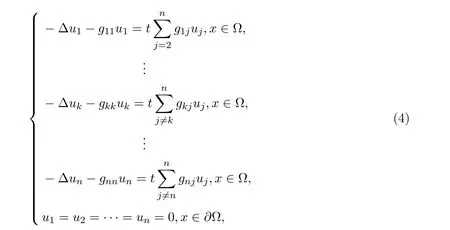
把第k个方程两边都乘以uk,k=1,2,···,n,同时在Ω上积分,再利用格林第一公式就可以得到

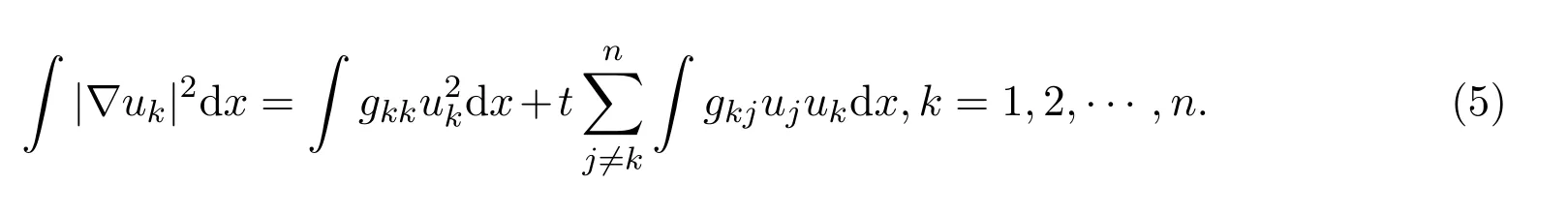
利用Holder不等式,Poincare不等式和Cauchy不等式,得到

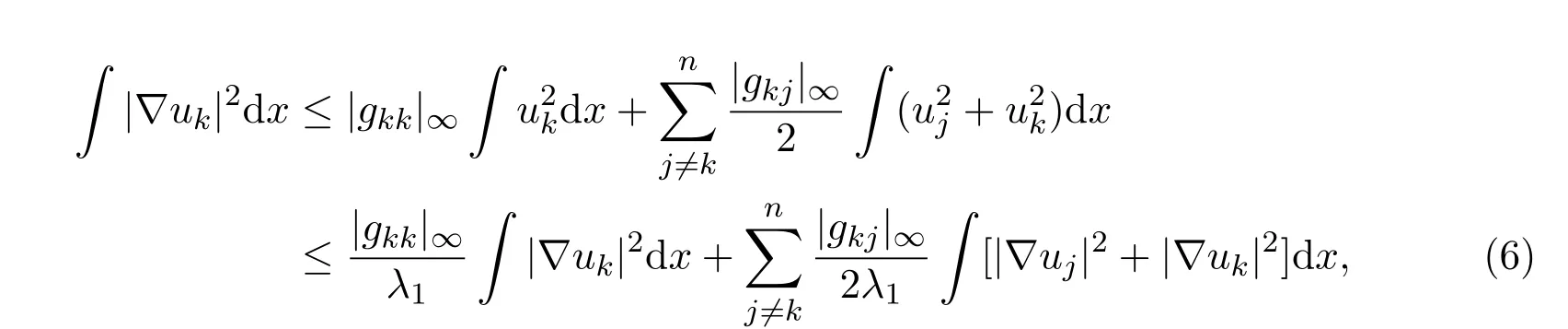
将上面每个式子相加便得到

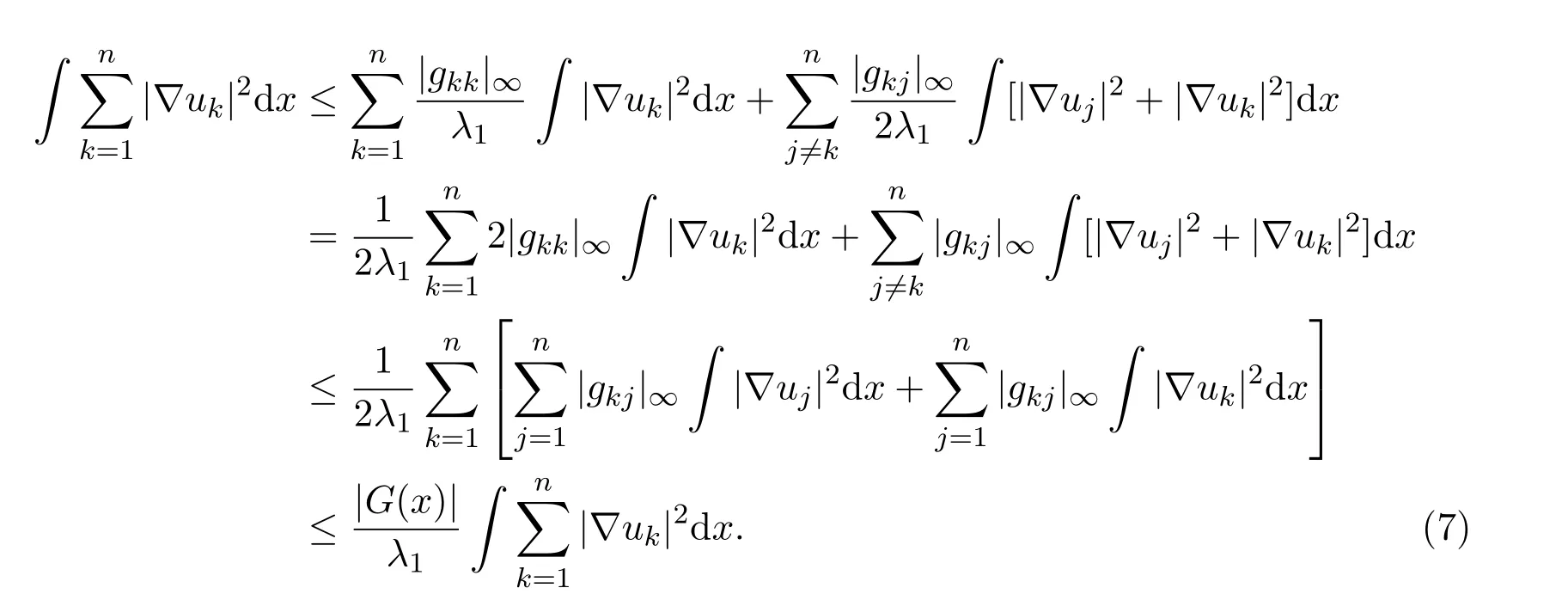
又因为|G(x)|<λ1,可得

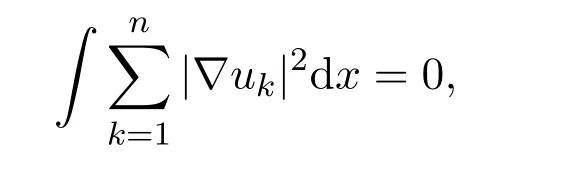
所以

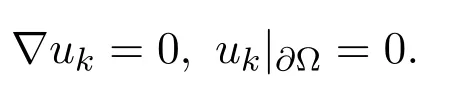
故得到

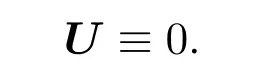
定理 2.2[4-5]如果|G(x)|<λ1,,那么方程组(2)存在正解而且有界.

证明令

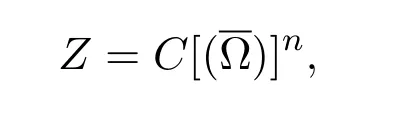
Z中各项都非负.∂Ω上面的零向量函数构成正锥K,所以K为Z的闭凸集.作一算子T:K→K,使得对U∈K,有

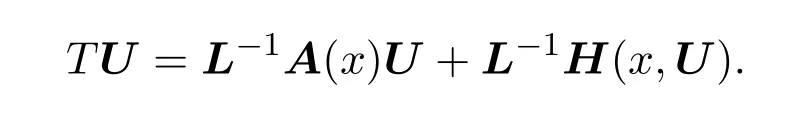
根据定理2.1可知,L−1为线性紧正算子;又A(x),H(x,U)中每一项连续非负,从而

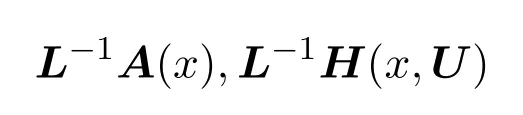
也是紧正算子.可知算子T:K→K是紧正算子.

下面利用反证法证明T满足引理的条件.

若T不满足引理的条件,则存在{tn}⊂[0,1],{Un}⊂K,当n→+∞时,

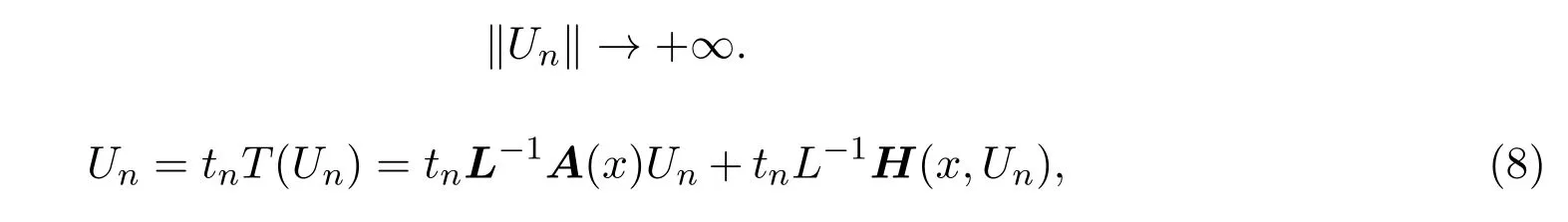
因为L−1,L−1A(x)为线性算子,令

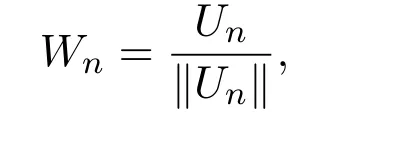
代入(8)式,得到

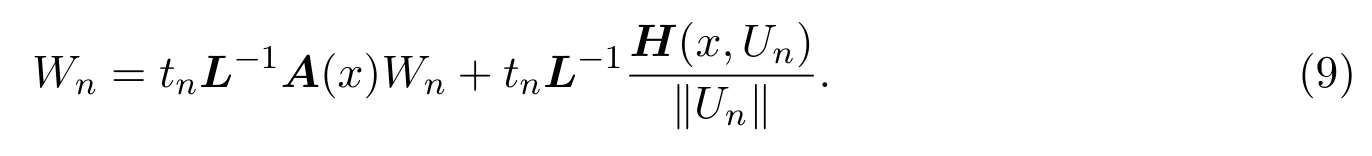
因为0≤H(x,Un)≤c,所以

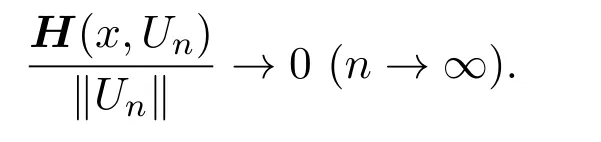
因为L−1A(x)为线性紧正算子,

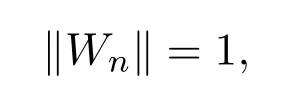
故是列紧集.所以通过取子列可得到tn→t0∈[0,1],L−1A(x)Wn收敛.所以

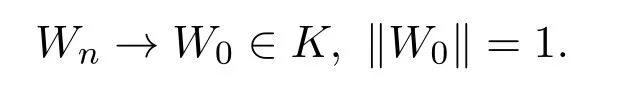
再对(9)式取极限便可得到

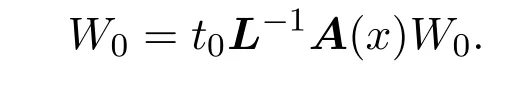
根据定理2.1的证明可知,W0≡0,显然与∥W0∥=1矛盾.从而T满足引理的条件,故T有一个不动点U∈K,∥U∥≤R,R是一个正常数.所以

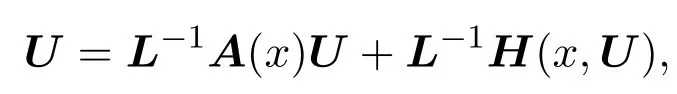
即

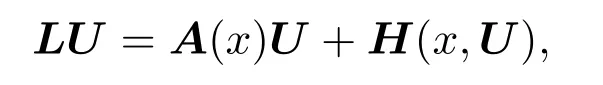
所以U为方程组(2)的解,而且有界.这也说明了方程组(1)存在有界正解.

如果对方程组(1)中的非线性项进行适当修改,还可以证明正解的唯一性.把方程组(1)中的H(x,U)改为

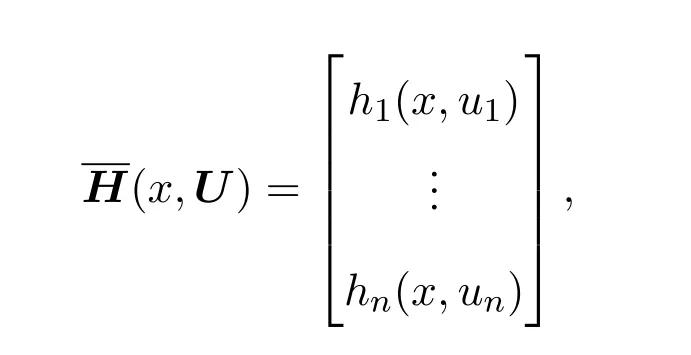
并且

(I)hk(x,uk),k=1,2,···,对于每一个变元连续;

(II)存在正常数c,对于 (x,uk)∈Rn+1,有 0≤hk(x,uk)≤c,k=1,2,···,n,成立;

(III)对于(x,uk)∈Rn+1,0≤hk(x,uk)≤c,k=1,2,···,n关于uk是单调递减的.考虑下面方程组:

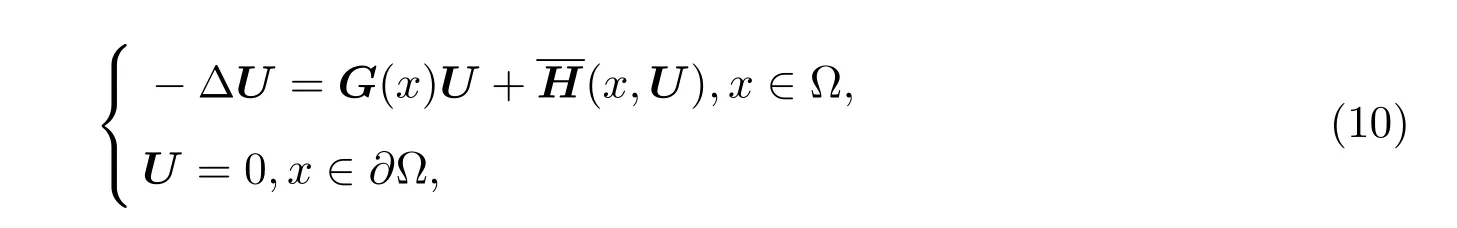
G(x),U和方程组(1)相同.

定理 2.3[6]如果|G(x)|<λ1,那么方程组(10)存在唯一解.

证明设

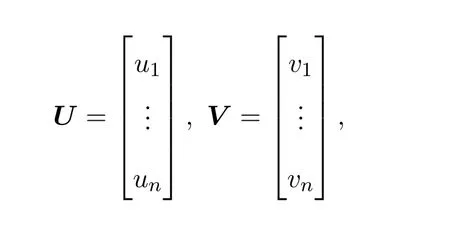
是方程组(10)的两个解,那么有

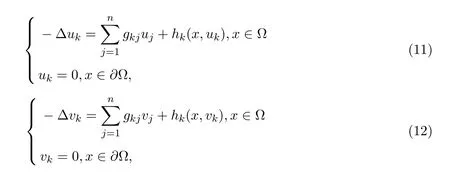
把上面两个方程两边乘以(uk−vk),得到

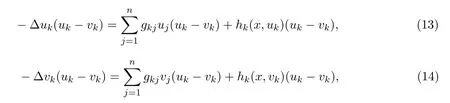
把(13)和(14)式在Ω上积分,再利用格林第一公式,得到

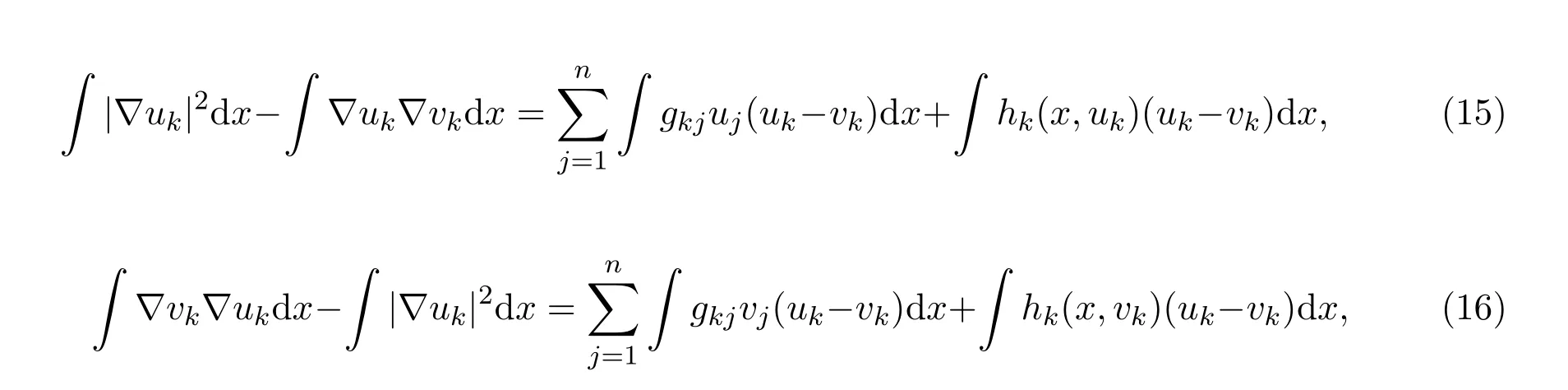
把 (15)式减去(16)式,得到

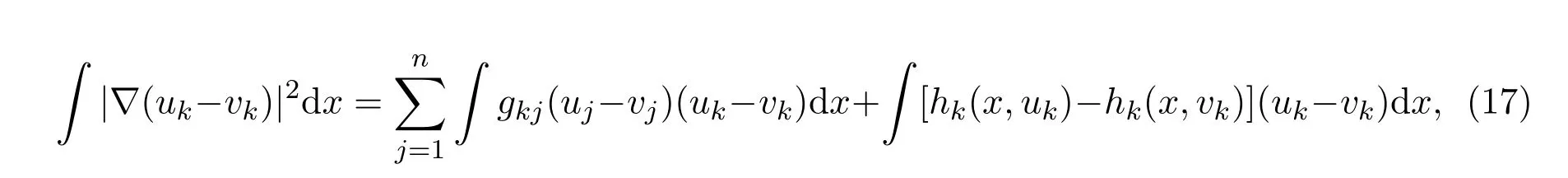
因为hk(x,uk),k=1,2,···,n关于uk是单调递减的,故

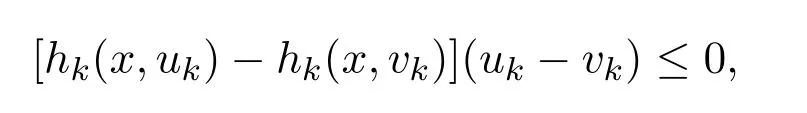
所以根据(17)式,得到

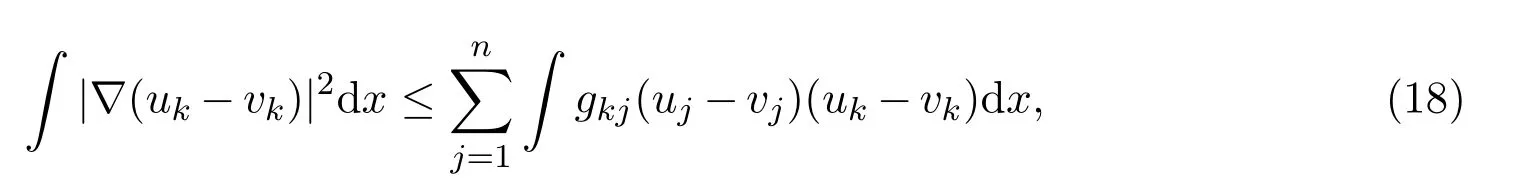
使用Holder不等式,Poincare不等式和Cauchy不等式,得到

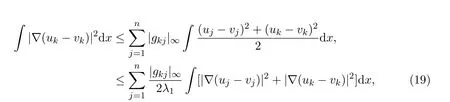
把上面n个不等式相加,得到

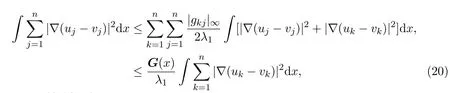
因为|G(x)|<λ1,所以得到

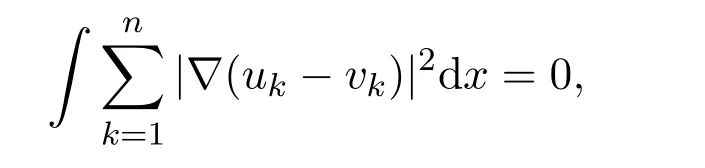
根据得到

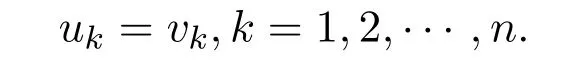
从而U≡V,所以方程组(10)存在唯一解.

[1]Deimling K.Nonlinear Functional Analysis[M].Berlin:Springer,1985.

[2]金启胜,周宗福.一类半线性椭圆型方程组边值问题的可解性[J].纯粹数学与应用数学,2017,33(3):248-253.

[3]Gilbarg D,Trudinger N S.Elliptic Partical Di ff erential Equations of Second Order[M].Berlin:Springer,1983.

[4]Dalmass R O.Existence and uniqueness of positive solutions of semilinear elliptic systems[J].Nonlinear Analysis,2000,39:559-568.

[5]Han Pigong.Multiple positive solutions of nonhomogeneous elliptic systems involving critical sovolev exponents[J].Nonlinear Anal.,2006,64:869-886.

[6]钟金标,陈祖墀.一类拟线性方程组的可解性[J].应用数学学报,2003,26(3):420-426.