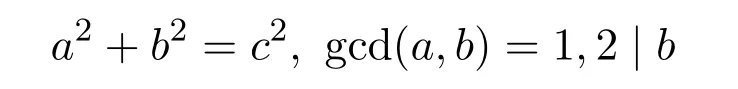与Euler函数φ(n)有关的非线性方程的正整数解
2018-06-23郑璐高丽郭梦媛
郑璐,高丽,郭梦媛
(延安大学数学与计算机科学学院,陕西 延安 716000)
1 引言
n是一正整数,令φ(n)为Euler函数.Euler函数φ(n)是数论中的一类极其重要函数之一,有关φ(n)方程解的研究可以说是数论研究中的一个极富意义的研究课题之一,引起了不少学者的关注及重视,也得到了一些结论,如文献[1-6].
对于形如

的Euler函数φ(n)的线性方程已有很多研究.文献[7]讨论了方程(1)当k为素数的情形,给出了k=3时方程(1)的部分解,而文献[8]给出了k=3时方程(1)的全部解;文献[9]给出了k=4时方程(1)的全部解;文献[10]讨论了当k=4,6时方程(1)的各自解;文献[11]给出了k=5时方程(1)的全部解.
对于形如
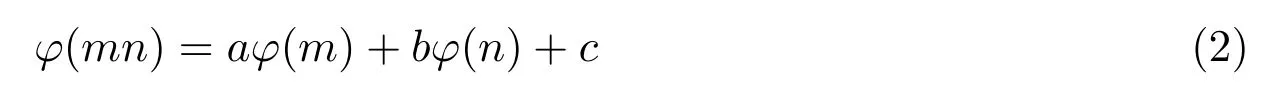
的Euler函数φ(n)的非线性方程,文献[12]讨论了当a=7,b=8,c=16的情形时方程(2)的全部解.
本文将讨论形如
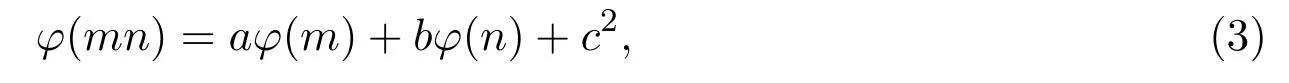
当a,b,c为勾股数且gcd(a,b,c)=1的Euler函数φ(n)非线性方程的整数解.
2 相关引理[13]
引理2.1对任意正整数m与n,若
引理 2.2对任意正整数m与n,则
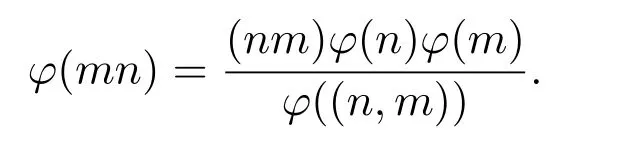
引理 2.3当n≥2时,φ(n) 定理3.1方程 无正整数解. 证明设gcd(mn)=d,则φ(m)=m1φ(d),φ(n)=n1φ(d),其中m1,n1∈Z+.由方程 (4)得 从而有φ(d)=1,5,25. 由引理2.3可得φ(d)=1,d=1,2. 当d=1时,有m1n1−3m1−4n1=25,从而有(m1−4)(n1−3)=37,根据因式与因式的所有可能关系,可以得到(m1,n1)=(5,40),(41,4).此时φ(m)与φ(n)两者中至少有一个为大于1的奇数,即方程(4)无解. 当d=2时,有 2m1n1−3m1−4n1=25,从而有 (m1−2)(2n1−3)=31,根据因式与因式的所有可能关系,可以得到(m1,n1)=(3,17),(33,2).此时φ(m)与φ(n)两者中至少有一个为大于1的奇数,即方程(4)无解. 综上所述方程(4)无正整数解. 定理3.2方程 无正整数解. 证明设gcd(mn)=d,则φ(m)=m1φ(d),φ(n)=n1φ(d),其中m1,n1∈Z+.由方程 (5)得 从而有φ(d)=1,13,169. 由引理2.3可得φ(d)=1,d=1,2. 当d=1时,有m1n1−5m1−12n1=25,从而有(m1−12)(n1−5)=229,根据因式与因式的所有可能关系,可以得到 (m1,n1)=(13,234),(241,6),此时φ(m)与φ(n)两者中至少有一个为大于1的奇数,即方程(5)无解. 当d=2时,有2m1n1−5m1−12n1=169,从而有(m1−6)(2n1−5)=199,根据因式与因式的所有可能关系,可以得到(m1,n1)=(7,102),(205,3),此时φ(m)与φ(n)两者中至少有一个为大于1的奇数,即方程(5)无解. 综上所述方程(5)无正整数解. 定理3.3方程 无正整数解. 证明设gcd(mn)=d,则φ(m)=m1φ(d),φ(n)=n1φ(d),其中m1,n1∈Z+.由方程 (6)得 从而有φ(d)=1,5,25,125,625. 由引理2.3可得φ(d)=1,d=1,2. 当d=1时,有m1n1−7m1−24n1=625,从而有 (m1−24)(n1−7)=793,根据因式与因式的所有可能关系,可以得到(m1,n1)=(25,801),(817,18),(37,78),(85,30),此时φ(m)与φ(n)两者中至少有一个为大于1的奇数,即方程(6)无解. 当d=2时,有2m1n1−7m1−24n1=625,从而有 (m1−12)(2n1−7)=709,根据因式与因式的所有可能关系,可以得到(m1,n1)=(13,358),(721,4),此时φ(m)与φ(n)两者中至少有一个为大于1的奇数,即方程(6)无解. 综上所述方程(6)无正整数解. 定理 3.4当a,b为任意的一奇一偶,c为任意的奇数,且满足 时,方程 无正整数解. 证明设gcd(mn)=d,则φ(m)=m1φ(d),φ(n)=n1φ(d),其中m1,n1∈Z+.由方程 (7)得 从而有φ(d)=1,c,c2. 因为c为任意的奇数,所以c2也为奇数,由引理2.3可得φ(d)=1,d=1,2. 当d=1时,有m1n1−am1−bn1=c2,从而有 假设方程(7)有整数解,则由引理2.3可知φ(m),φ(n)必为偶数,即m1,n1为偶数.因为a,b为任意的一奇一偶,由整除的性质可知,2|m1−b,2-n1−a.即 又c为任意的奇数,所以因此对于(m1−b)(n1−a)=c2+ab,左右矛盾,因此方程(7)无解. 当d=2时,有 2m1n1−am1−bn1=c2,从而有 假设方程(7)有整数解,则由引理2.3可知φ(m),φ(n)必为偶数,即m1,n1为偶数.因为a,b为任意的一奇一偶,由整除的性质可知,即 又c为任意的奇数,所以因此对于 左右矛盾,因此方程(7)无解. 综上所述方程(7)无正整数解. Euler函数φ(n)是数论中的一个重要函数,关于Euler函数的一些重要性质与之有关的不定方程的正整数解,目前仍是数论中一个重要问题.本文讨论形如 的Euler函数φ(n)非线性方程的整数解.给出了当(a,b,c)=(3,4,5),(5,12,13),(7,24,25)时无正整数解,并证明了当a,b为任意的一奇一偶,c为任意的奇数,且满足 时,方程无正整数解. [1]张四保.三类包含Euler函数的方程[J].数学的实践与认识,2016,44(8):287-291. [2]张四保,刘启宽.关于Euler函数一个方程的正整数解[J].东北师大学报(自然科学版),2015,47(3):49-54. [3]张四保,杜先存.一个包含Euler函数方程的正整数解[J].华中师范大学学报(自然科学版),2015,49(4):497-501. [4]张文鹏.关于F.Smarandache函数的两个问题[J].西北大学学报(自然科学版),2008,38(2):173-176. [5]范盼红.关于F.Smarandache函数和欧拉函数的三个方程[J].黑龙江大学自然科学学报,2012,29(5):626-628. [6]Yi Yuan.An equation involving the Euler function and Smarandache function[J].Scientia Magan,2005,1(2):172-175. [7]Sun Cuifang,Cheng Zhi.Some kind of equations involving Euler functionφ(n)[J].数学研究,2010,43(4):364-369. [8]张四保.有关Euler函数φ(n)方程的正整数解[J].数学的实践与认识,2014,44(20):302-305. [9]许霞,徐小凡.关于欧拉方程φ(ab)=2k(φ(a)+φ(b))的正整数解 [J].西南师范大学学报 (自然科学版),2015,41(4):6-9. [10]管春梅,张四保.与Euler函数φ(n)有关的两个方程[J].数学的实践与认识,2016,46(9):221-225. [11]鲁伟阳,高丽,王曦浛.有关Euler函数φ(n)的方程的可解性问题[J].江西科学,2016,34(1):15-16. [12]夏衣旦·莫合德,张四保,熊满玉.一个有关Euler函数的非线性方程的解[J].首都师范大学学报(自然科学版),2018,39(2):4-7. [13]Rosen K H.Elementary Number Theory and its Applications[M].5th ed.New Jersey:Pearson Educatin,Inc.,Addison Wesley,2005.3 定理及其证明
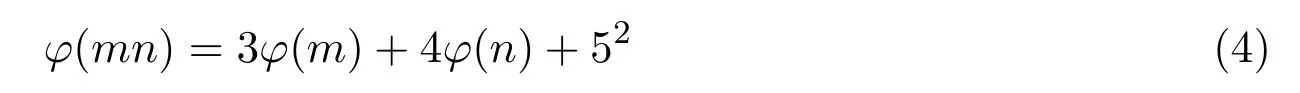
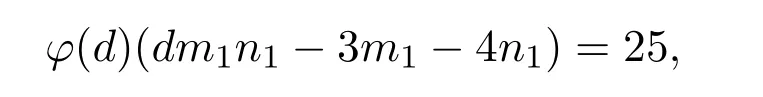
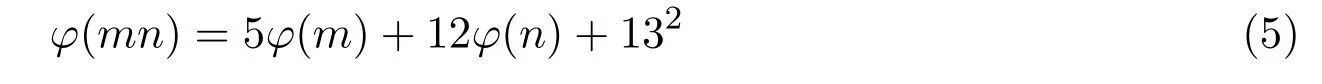
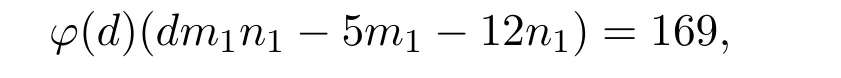
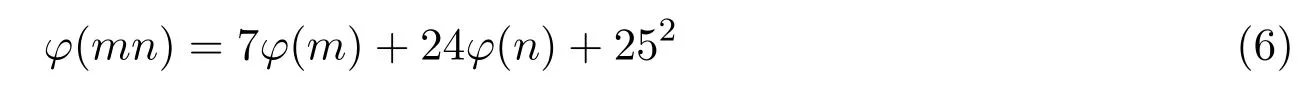
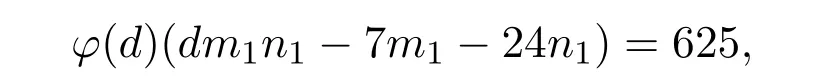
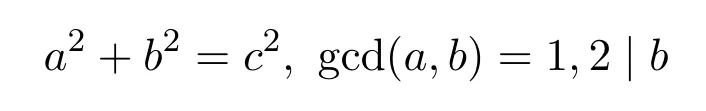
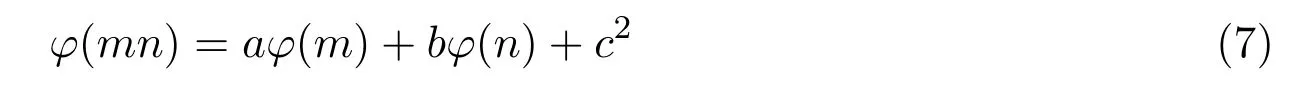
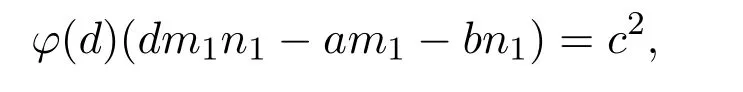
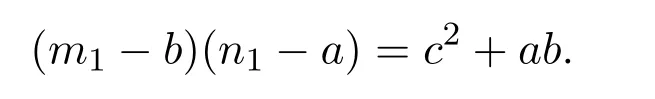
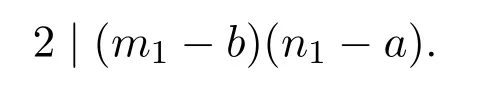
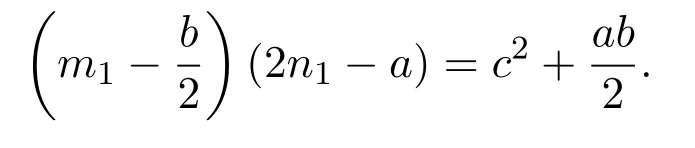
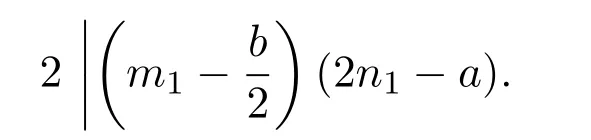
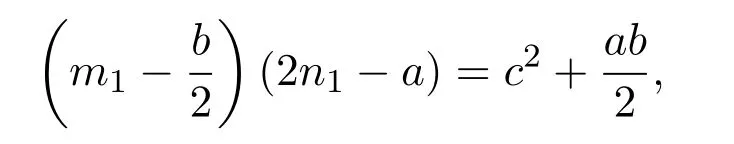
4 结论