具不变主对角线元矩阵新的特征值包含集

李静,李耀堂

(云南大学数学与统计学院，云南 昆明 650500)

1 引言

矩阵的特征值定位在许多科学和工程领域中有着广泛的应用[1-4],是矩阵理论及其应用的重要研究内容.在文献[5]中作者通过考虑矩阵的结构,给出了一些特殊矩阵类的特征值包含区域,特别是对具不变主对角线元矩阵,即

给出了如下的Gersgorin圆盘集ΓR(A)和Brauer卵型集K(A):

其中

此外,作者还给出了具不变主对角线元矩阵的如下新的特征值包含区域.

定理 1.1[5]设则

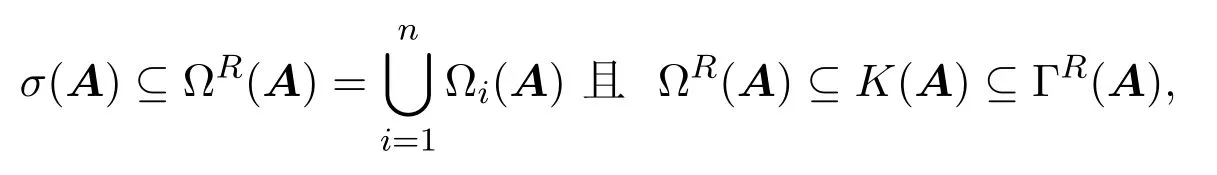
其中

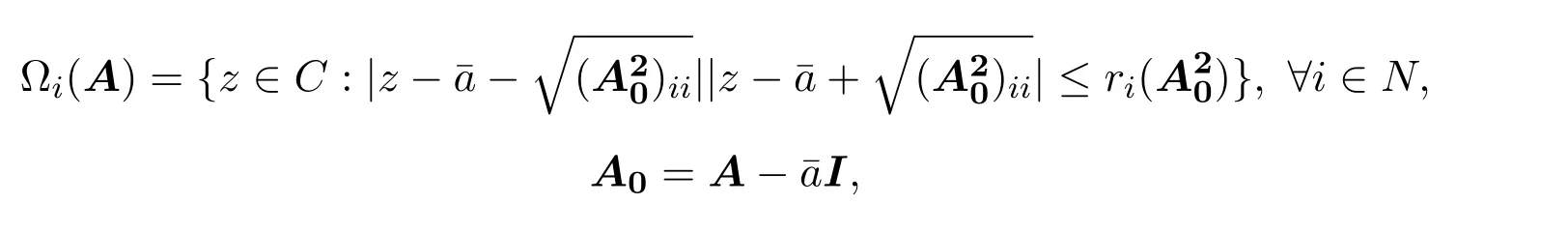
(A20)ij为矩阵A20的第(i,j)元素.

文献[6]中给出具不变主对角线元矩阵非奇异的一个充分条件,由此得到具不变主对角线元矩阵的另一个特征值包含集.

定理1.2[6]设则

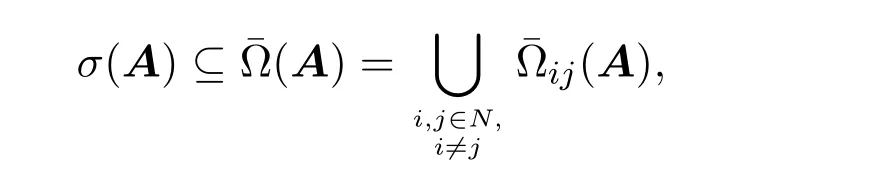
其中

文献[6]中证明了

对于矩阵特征值定位问题,人们总是希望能用尽可能少的计算量得到尽可能精确的特征值包含区域,但目前得到的结果仍远远没有达到人们的期望,因此有必要继续对其进行探讨和研究.本文将继续研究文献[6]中给出的具不变主对角线元矩阵非奇异的充分条件,期望能由此得到新的特征值定位集.

2 具不变主对角线元矩阵新的特征值包含集

为下文叙述和证明方便,首先给出一些定义和定理.

定义2.1[7]设A=[aij]∈Cn×n(n≥2),S是N的非空真子集,为S的补集.若

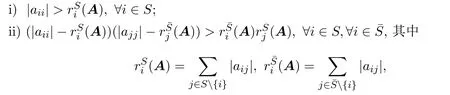
则称A为S-严格对角占优矩阵(简称为S-SDD矩阵).

定理 2.1[7]设A=[aij]∈Cn×n(n≥2)为S-SDD矩阵,则A是非奇异的.

定理2.2[7]设A=[aij]∈Cn×n(n≥2),S是N的非空真子集,则

其中

定理2.3[6]设是N的非空真子集若

其中则A是非奇异的.

定理2.4设是N的非空真子集,则

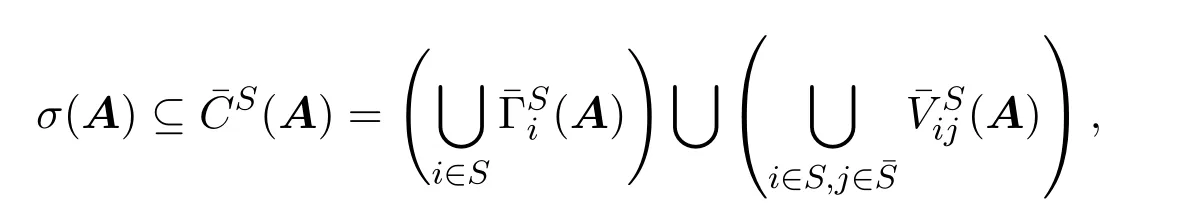
其中对任意的

下面我们比较定理2.3和定理1.1的结论.

定理2.5设是N的非空真子集,则

3 Toeplitz矩阵的特征值包含集

在第二节中得到具不变主对角线元矩阵新的特征值包含集,而Toeplitz矩阵是一类特殊的具不变主对角线元矩阵.下面对Toeplitz矩阵的特征值包含集进行讨论.为下文叙述方便,先给出一些定义和定理.

定义 3.1[5]设T=[tij]∈Cn×n(n≥2),如果T具有如下形式:

则称T为Toeplitz矩阵.

Toeplitz矩阵类是具不变主对角线元矩阵类的一个子类,在诸如信号处理,微分与积分方程,概率论与统计学,马尔可夫链等许多领域都有着重要的应用.文献[5]中给出了Toeplitz矩阵的一个特征值包含集.

定理 3.1[5]设T=[tij]∈Cn×n(n≥2)为Toeplitz矩阵且tii=t0,∀i∈N,则

其中

文献[8]进一步给出了Toeplitz矩阵的如下特征值包含集.

定理 3.2[8]设T=[tij]∈Cn×n(n≥2)为Toeplitz矩阵,tii=t0,∀i∈N,则

其中

定理 3.3[8]设T=[tij]∈Cn×n(n≥2)为Toeplitz矩阵,tii=t0,∀i∈N.则

其中同定理3.2,

将定理2.4应用到Toeplitz矩阵,可以得到如下结果.

定理 3.4设T=[tij]∈Cn×n(n≥2)为Toeplitz矩阵,tii=t0,∀i∈N,S是N的非空真子集,

则

其中对任意的

4 数值例子

本节用几个数值例子对本文所得结果进行说明.

例 4.1考虑下面矩阵(文献[5]中的A4):

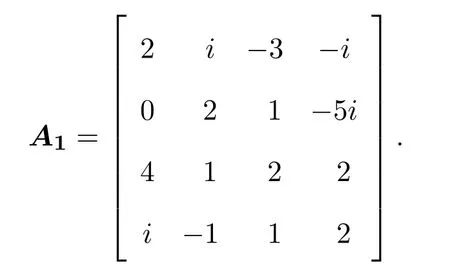
取S={2,4},分别将Gersgorin圆盘定理,Brauer卵型定理,定理1.1和定理2.4应用于矩阵A1,得到A1的特征值包含集ΓR(A1),K(A1),ΩR(A1)和其包含关系如图1所示.图中星号表示矩阵A1的特征值,图形中的区域从外到内依次表示为ΓR(A1),K(A1),ΩR(A1)和图1表明,因此更精确的定位了矩阵A1的特征值.

图1 S(A1)⊂ΩR(A1)⊂K(A1)⊂ΓR(A1)

例 4.2考虑下面矩阵(文献[5]中的A3)

取S={2,4},分别将定理2.2,定理1.1和定理2.4应用于矩阵A2,得到A2的特征值包含集CS(A2),ΩR(A2)和其关系如图2所示.

图中星号表示矩阵A2的特征值,图形中的区域从外到内依次表示为CS(A2),ΩR(A2)和由图2知

图2 S(A2)⊂CS(A2)

例 4.3考虑例4.1中的矩阵A1(文献 [5]中的A4).取S={2,4},分别将 Gersgorin圆盘定理,Brauer卵型定理,定理1.1,定理1.2和定理2.4运用到矩阵A1,得到A1的特征值包含集其关系如图3所示.

图中星号表示矩阵A1的特征值,图形中的区域从外到内依次表示为ΓR(A1),K(A1),图3表明,因此更精确的定位了矩阵A1的特征值.

图3 S(A1)⊂(A1)⊂ΩR(A1)⊂K(A1)⊂ΓR(A1)

例 4.4考虑如下的Toeplitz矩阵(文献[5]中的Q)

取S={1,4},分别将Gersgorin圆盘定理,Brauer卵型定理,定理3.1和定理3.4运用到特矩阵T上,得到T的征值包含集ΓR(T),K(T),Ω(T)和S(T),其关系如图4所示.

图中星号表示矩阵T的特征值,图形中的区域从外到内依次表示为ΓR(T),K(T),Ω(T)和图4表明,因此更精确的定位了矩阵T的特征值.

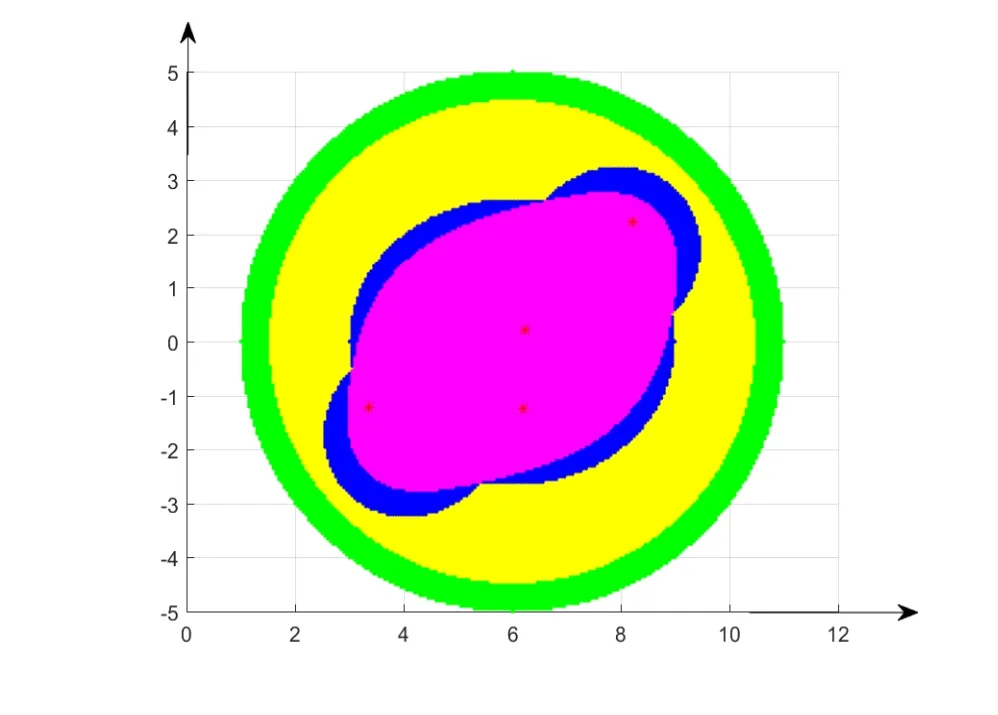
图4 S(T)⊂Ω(T)⊂K(T)⊂ΓR(T)

例 4.5考虑例 4.4中的矩阵T.取S={1,4},分别将定理3.1,定理3.2,定理 3.3和定理3.4运用到矩阵T上,得到T的特征值包含集其关系如图5所示.

图中星号表示矩阵T的特征值,图形中的区域从外到内依次表示为Ω(T),Ω1(T),从图中不难发现但

图5 Ω2(T)⊆Ω1(T)⊆Ω(T),S(T)⊆Ω(T)

[1]Cvetkovic L,Kostic V,Bru R,et al.A simple generalization of Gerschgorin′s theorem[J].Advances in Computational Mathematics,2011,35:271-280.

[2]Cvetkovic L.H-matrix theory vs.eigenvalue localization[J].Numer.Algor.,2006,42:229-245.

[3]Li C Q,Li Y T.Generalization of Brauer′s eigenvalue localization theorem[J].Electronic Journal of Linear Algebra,2011,22:1168-1178.

[4]Cvetkovic L J,Kostic V,Pena J M.Eigenvalue localization re finements for matrices related to positivity[J].SIAM Journal on Matrix Analysis and Applications,2011,32:771-773.

[5]Melman A.Ovals of Cassini for Toeplitz matrices[J].Linear and Multilinear Algebra,2012,60(2):189-199.

[6]张卫倩.具相同主对角线元矩阵新的特征值包含区域[D].昆明:云南大学图书馆,2014.

[7]Cvetkovic L,Kostic V,Varga R S.A new Gersgorin-type eigenvalue inclusion set[J].Electronic Transactions on Numerical Analysis,2004,18:73-80.

[8]Li C Q,Li Y T.New regions including eigenvalues of Toeplitz matrices[J].Linear and Multilinear Algebra,2014,62(2):229-241.