抛物型交换四元数矩阵的性质及其逆矩阵求法

孔祥强

(菏泽学院数学与统计学院,山东 菏泽 274015)

1 引言

四元数量子力学是现代量子力学的重要分支,它是建立在非交换的四元数代数上的量子力学,与一般的复量子力学不同,其相应粒子的波函数及其振幅是由四元数来表示.1849年,James Cockle提出了非交换的分裂四元数,其形式为:

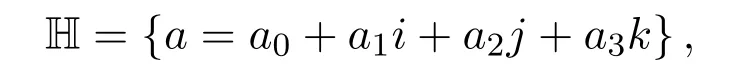
且满足

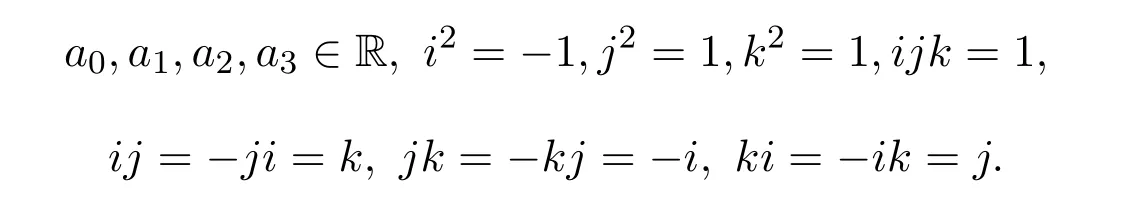
分裂四元数代数H不是除环,且含有零因子、幂零元和幂等元[1-4].对分裂四元数的研究得到了系列成果,见文献[5-6]等.文献[7]中首次研究了乘法满足交换性的新代数系统,即由交换四元数构成的系统,该系统和分裂四元数系统一样也是四维代数系统,但交换四元数代数含有零因子和同位元.近年来,对交换四元数代数理论的研究逐步引起学者们的重视,且研究成果在数学和物理学等学科中均有很好的应用[8-10],因此对交换四元数理论的研究显得十分必要.文献[11]介绍了交换四元数的分类情况,具体包括椭圆型交换四元数、抛物型交换四元数和双曲型交换四元数等,但对每一类交换四元数并没有做深入研究.文献[12]研究了椭圆型交换四元数及其矩阵,得到此类交换四元数的性质,给出了此类交换四元数矩阵的复表示形式.相比较而言,学者对抛物型交换四元数和双曲型交换四元数的研究很少.与文献[12]不同,本文研究的是抛物型交换四元数及其矩阵,利用矩阵的实表示,得到此类交换四元数及其矩阵的重要性质,并给出了求抛物型交换四元数矩阵逆矩阵的新方法,且该方法可通过计算机得以轻松实现.在本文结果的基础上,可进一步深入探讨抛物型交换四元数矩阵的特征值问题、可对角化问题、行列式问题、盖尔圆盘定理的推广问题等;在本文思路的基础上,还可展开对双曲型交换四元数及其矩阵的深入研究.

2 抛物型交换四元数

设R为实数域,

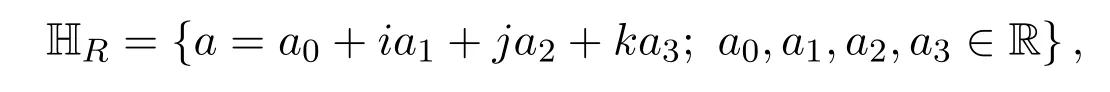
且满足

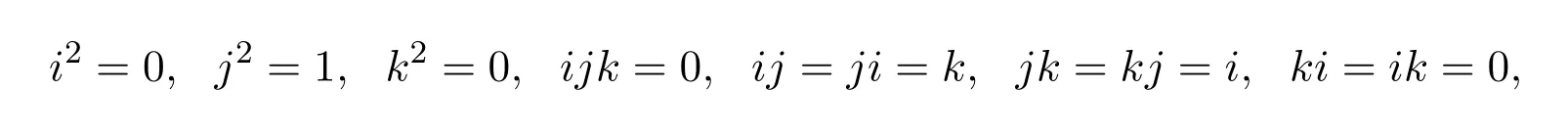
称满足条件的四元数a为抛物型交换四元数[11].

设

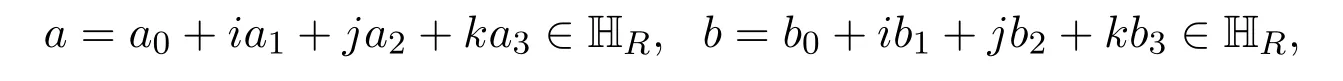
若ai=bi(i=0,1,2,3),称a与b相等.定义加法和乘法如下:

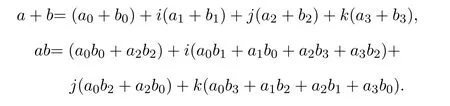
抛物型交换四元数的共轭分三种形式,分别记为:

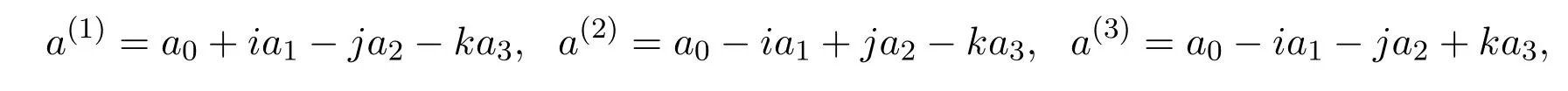
则

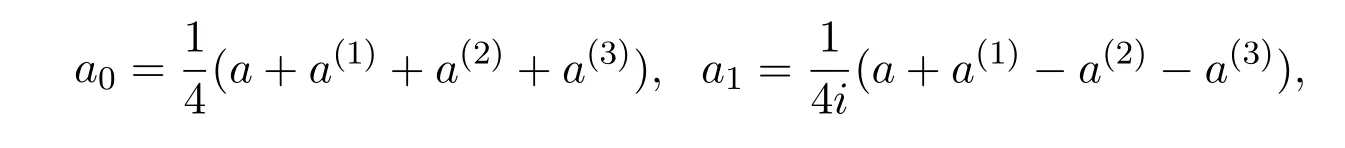
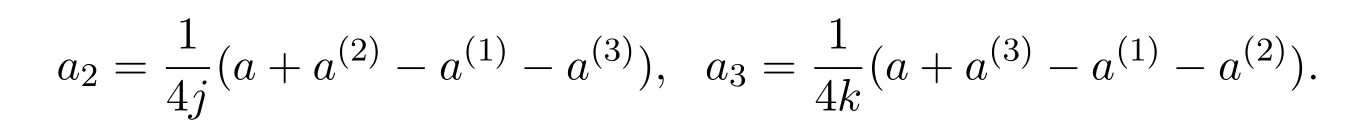
性质 2.1设a,b∈HR,s∈R,则

(1)si=is;sj=js;sk=ks;(2)a=a(1)⇔a∈C;C为复数域;(3)ab=ba.

证明由乘法定义知(1)成立.

(2)由

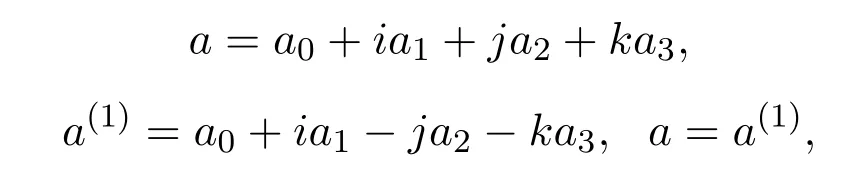
则

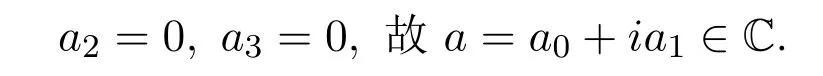
(3)因

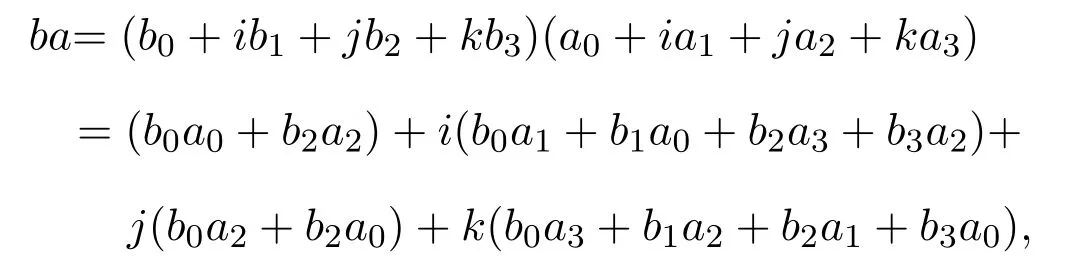
故

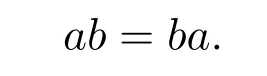
3 抛物型交换四元数的实表示

定理 3.1任何一个抛物型交换四元数都可以表示成实数域上的4阶矩阵.

证明设

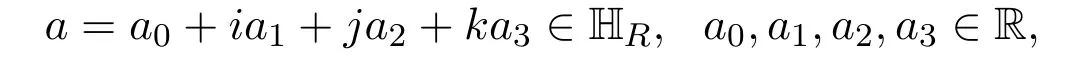
定义映射

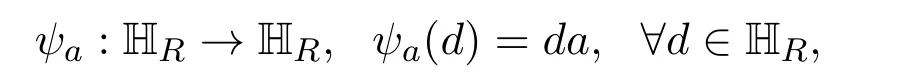
则映射为双射且

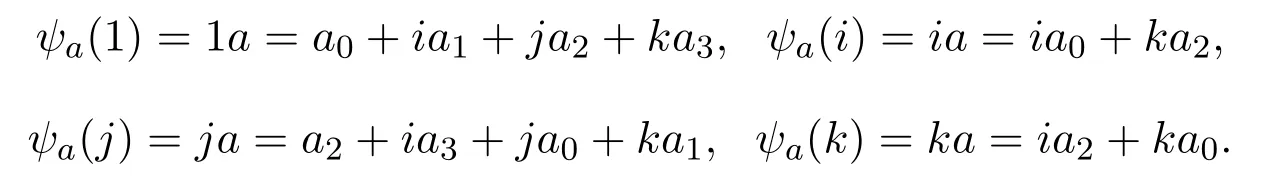
由此映射,可定义抛物型交换四元数集合为4×4实矩阵集合:

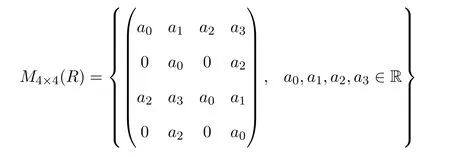
的子集合,HR和M4×4(R)本质是相同的.故对抛物型交换四元数的研究可转化为R上4×4矩阵的研究.R上4×4矩阵的性质即为HR上抛物型交换四元数的性质.称

为a的实表示,记为aR.

性质 3.1设a,b∈HR,ξ1,ξ2∈R,tr(aR)为aR的迹,则

(1)(ab)R=aRbR;(2)(ξ1a+ξ2b)R=ξ1aR+ξ2bR;(3)tr(aR)=a+a(1)+a(2)+a(3).

证明(1)

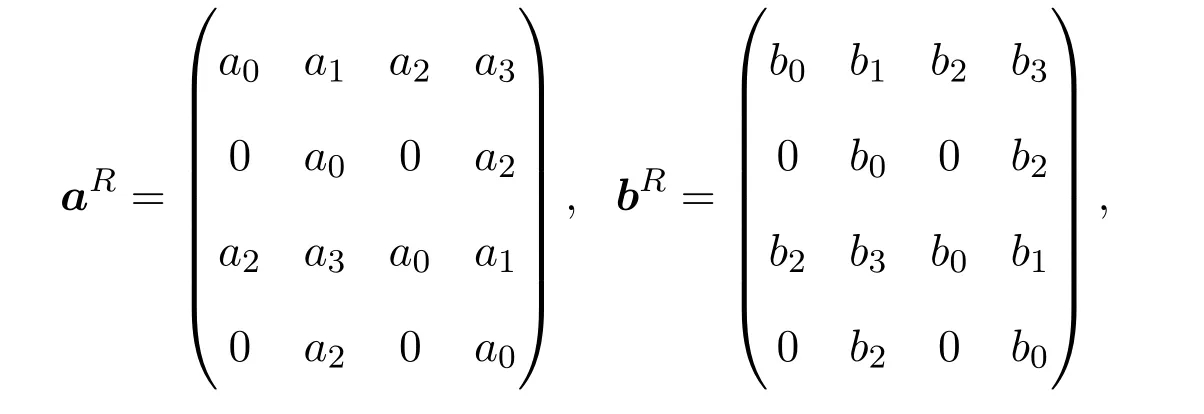
则

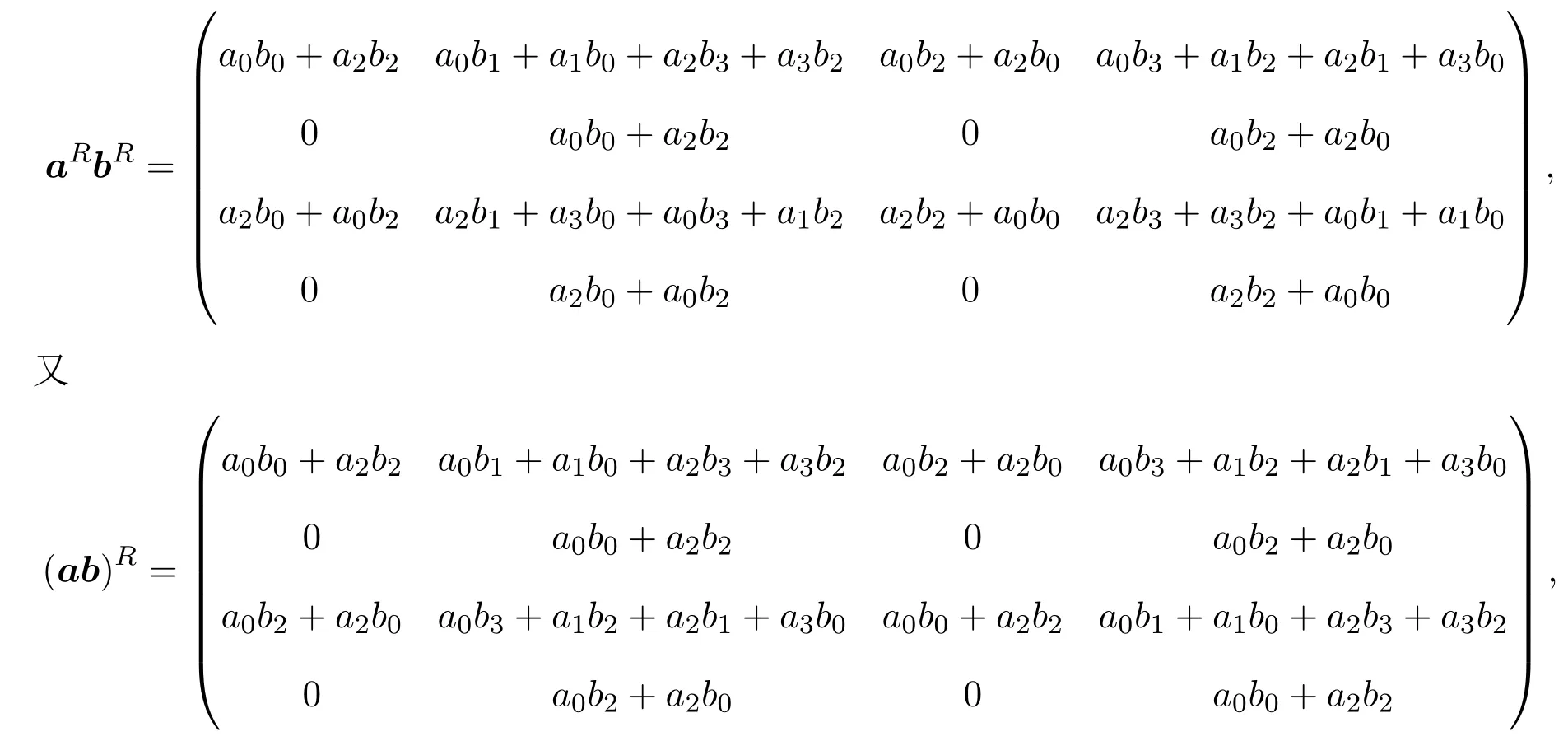
故

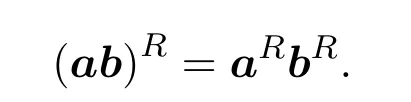
(2)与(1)中类似的方法可得

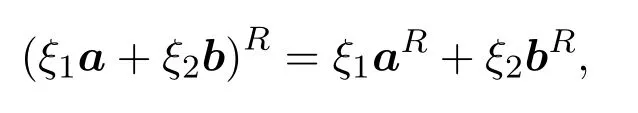
特别地,当ξ1=ξ2=1时,

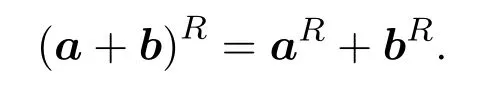
(3)由共轭及实表示定义

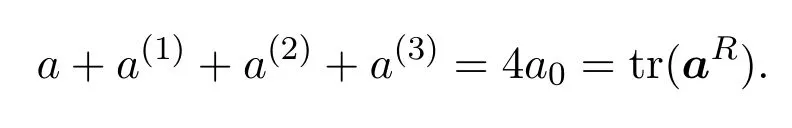
4 抛物型交换四元数矩阵及其性质

设

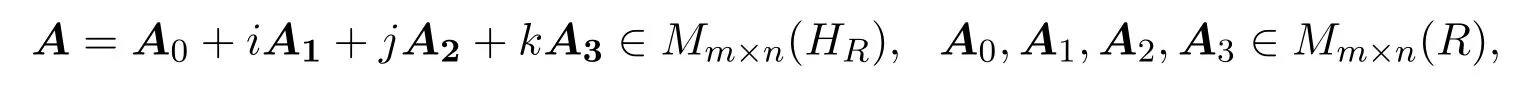
称A为一般的抛物型交换四元数矩阵.Ā表示A的共轭,AT表示A的转置,AH表示A的共轭转置.Mn×n(C)表示n阶复矩阵集合.对于B∈Mn×s(HR),a,b∈HR,有

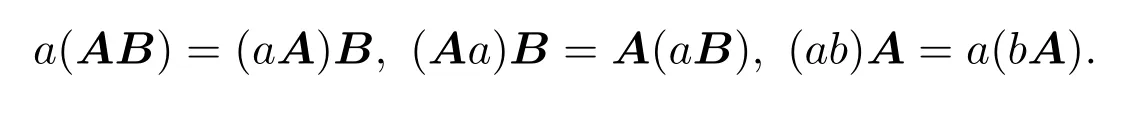
若

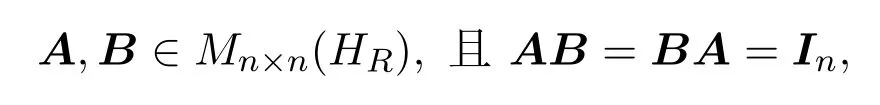
则称A为可逆矩阵,且

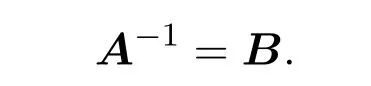
性质 4.1 设A,B∈Mn×n(HR),则

(1)(AB)T=BTAT;(2)若A,B均可逆,则(AB)−1=B−1A−1;(3)(AB)H=BHAH.

证明设

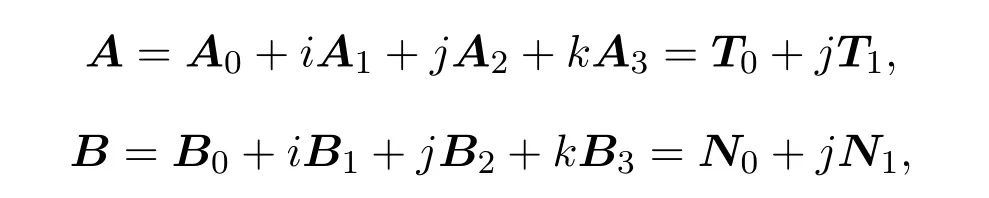
其中

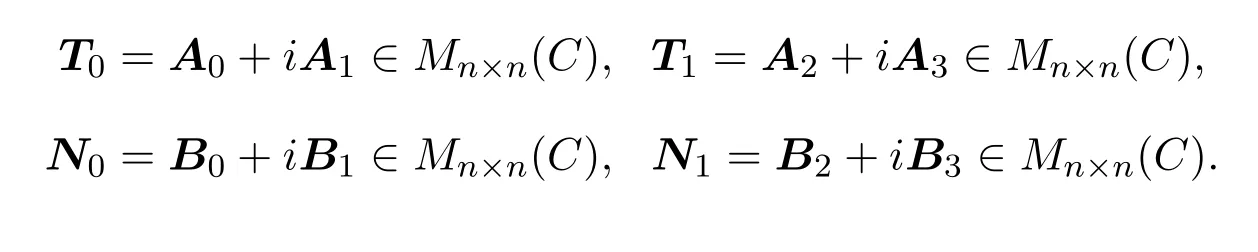
(1)

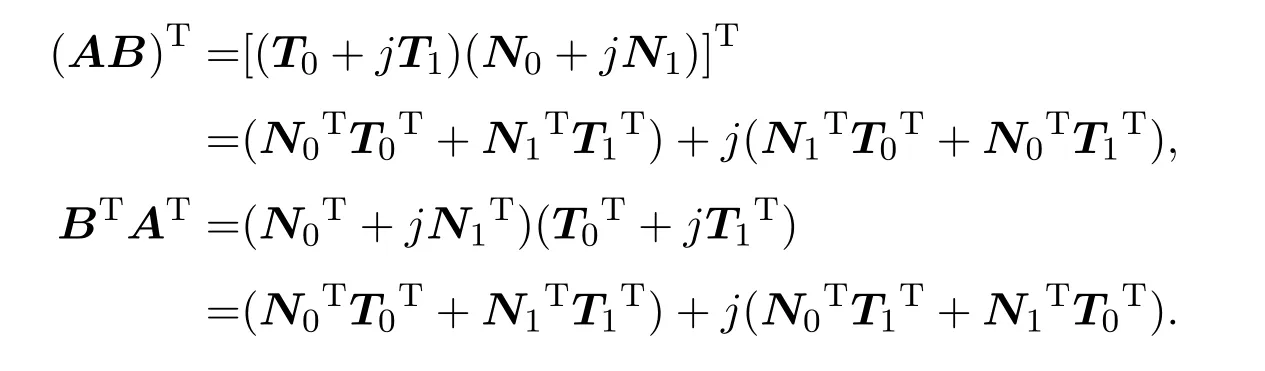
(2)由

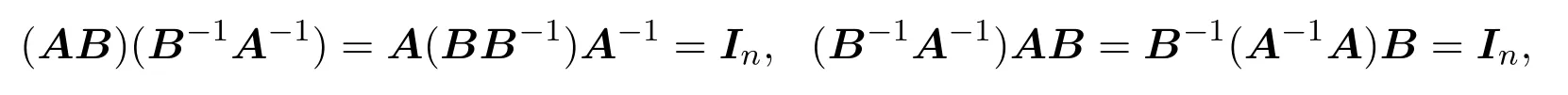
故AB可逆,且 (AB)−1=B−1A−1.

(3)对A∈Mm×n(HR)而言,其共轭矩阵有三种形式:

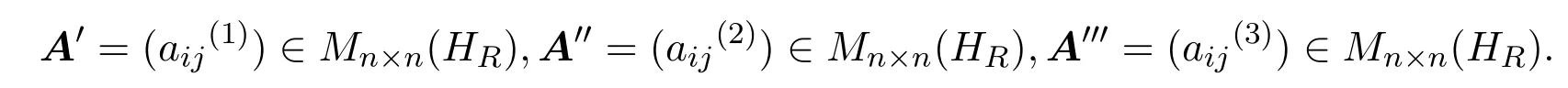
要证的结论即为:

① (AB)H=(B′)T(A′)T; ② (AB)H=(B′′)T(A′′)T; ③ (AB)H=(B′′′)T(A′′′)T.

证明如下：

①

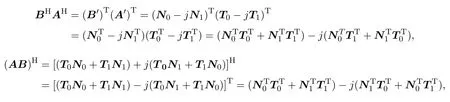
故

故

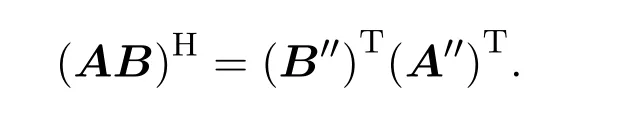
③

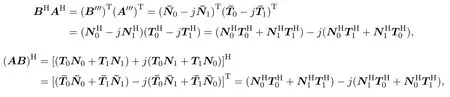
故

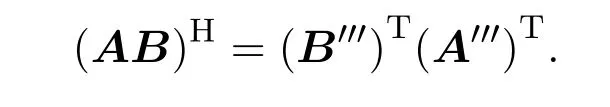
5 抛物型交换四元数矩阵的逆矩阵

定理 5.1设A,B∈Mn×n(HR),且满足BA=In,则AB=In.

证明因为

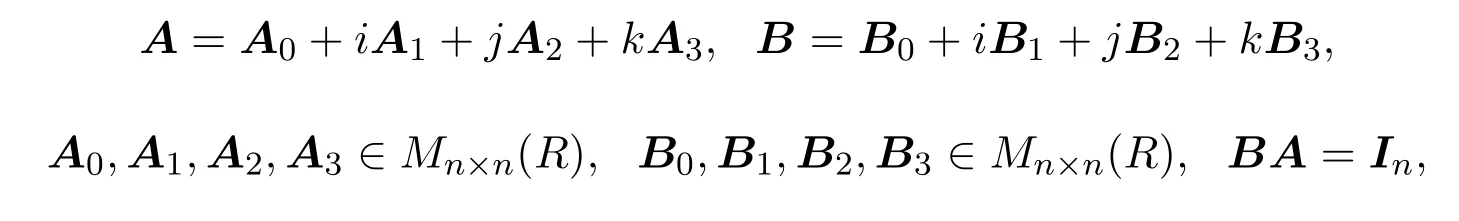
则

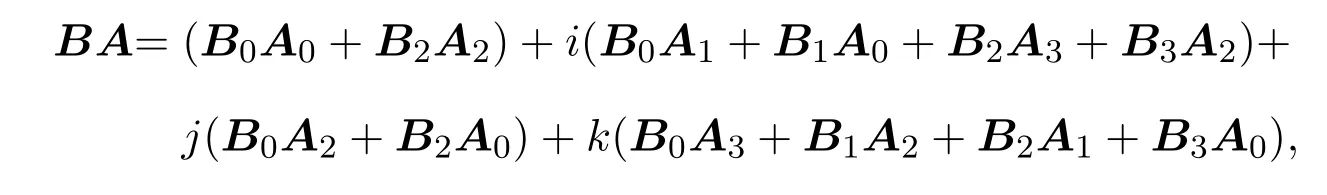
故

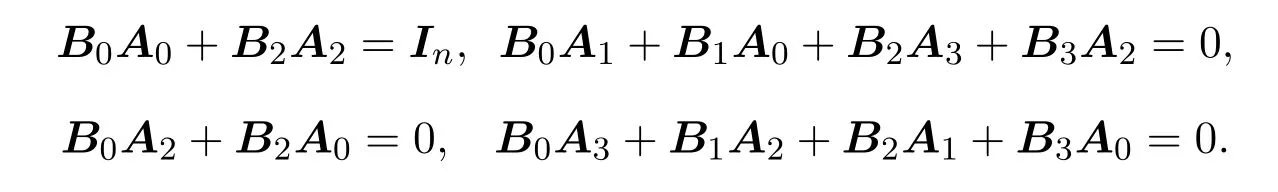
即

则

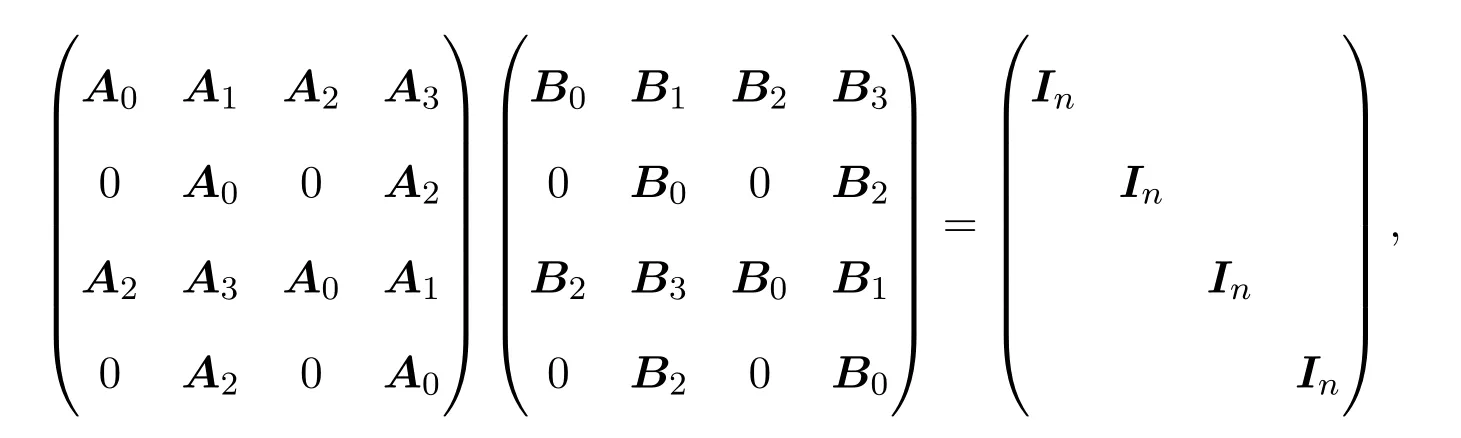
所以

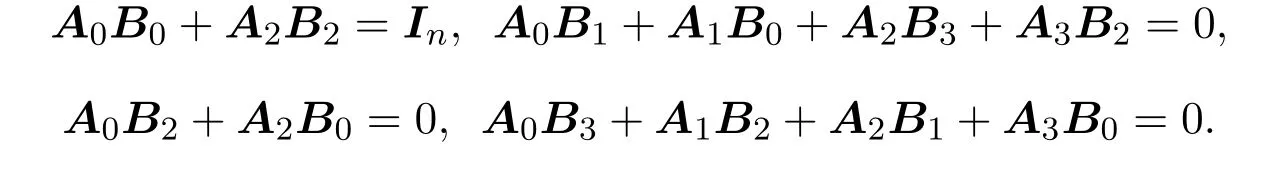
又

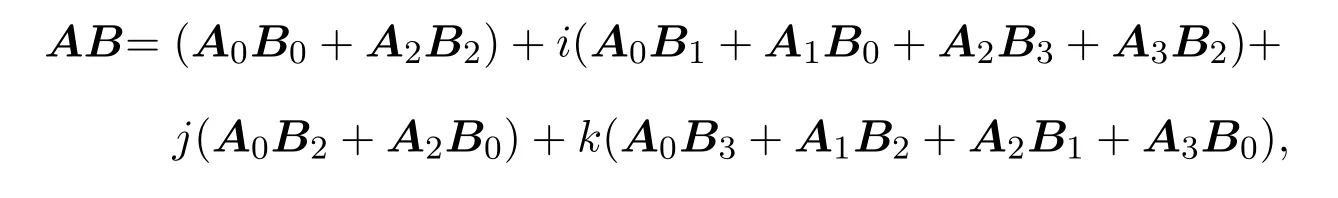
则

设

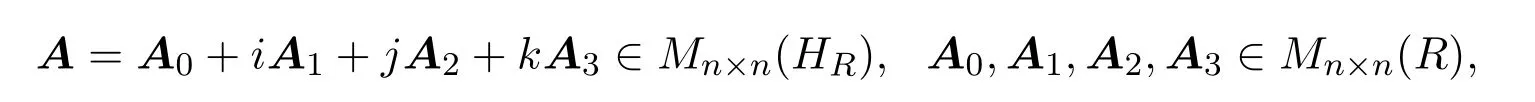
定义A的实表示矩阵为:

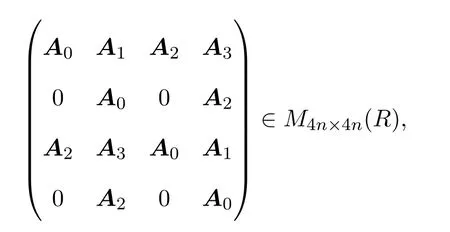
记为AR.

则Mn×n(HR)和M4n×4n(R)本质上是相同的,故对抛物型交换四元数矩阵的研究可转化为R上4n×4n矩阵的研究.R上4n×4n矩阵的性质即为HR上抛物型交换四元数矩阵的性质.

性质 5.1设A,B∈Mn×n(HR),则

(1)InR=I4n;(2)(A+B)R=AR+BR;

(3)(AB)R=ARBR;(4)若A可逆,则 (A−1)R=(AR)−1.

证明(1)由

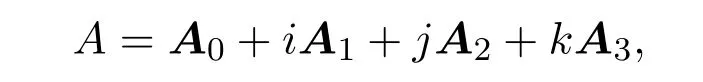
取

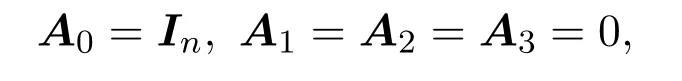
由实表示的定义,InR=I4n.

(2)由

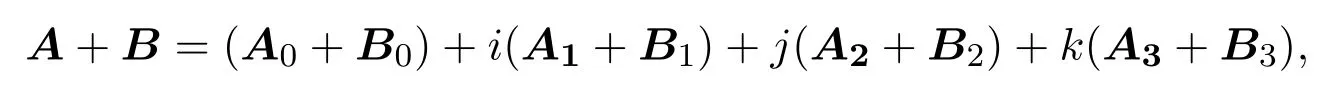
则

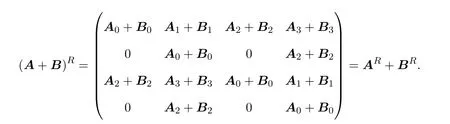
(3)利用与(2)类似的方法证得,

(4)由A−1存在,则

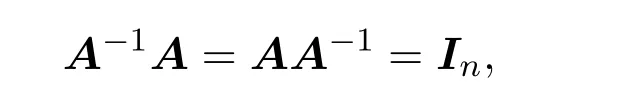
故

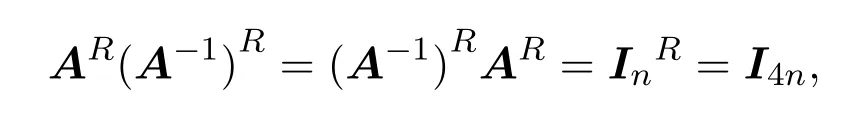
所以

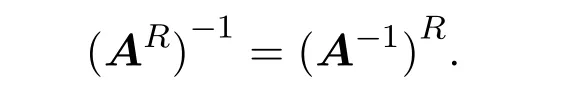
定理 5.2设A∈Mn×n(HR),AR可逆,且 (AR)−1∈M4n×4n(R),则A可逆.

证明由

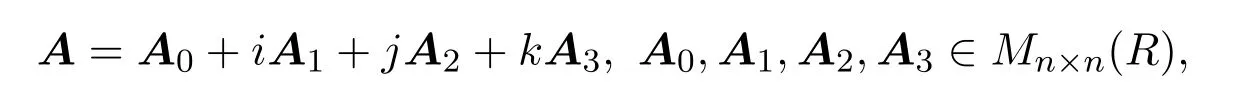
则

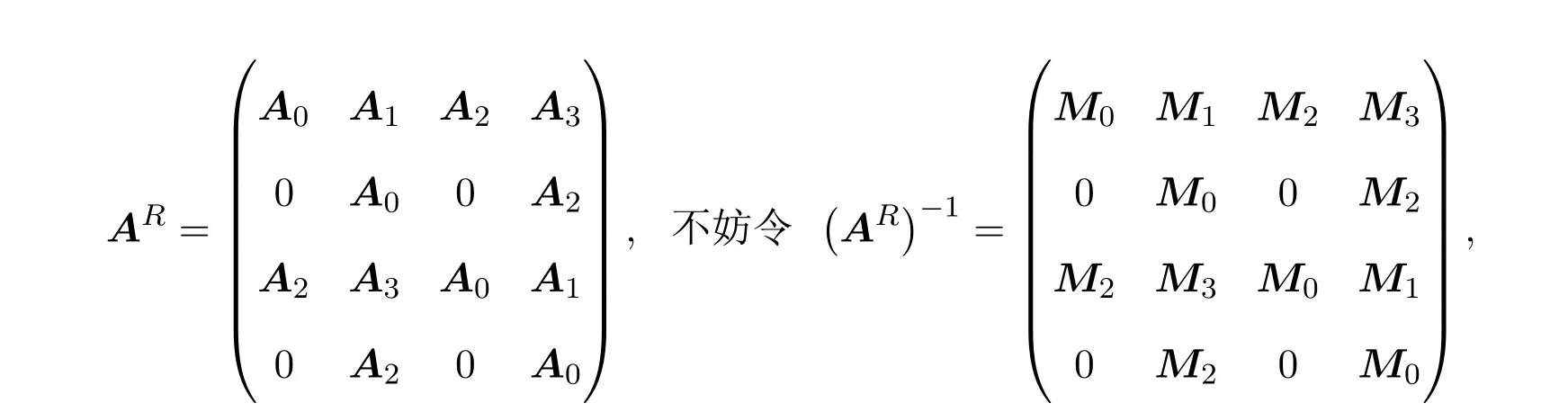
由于

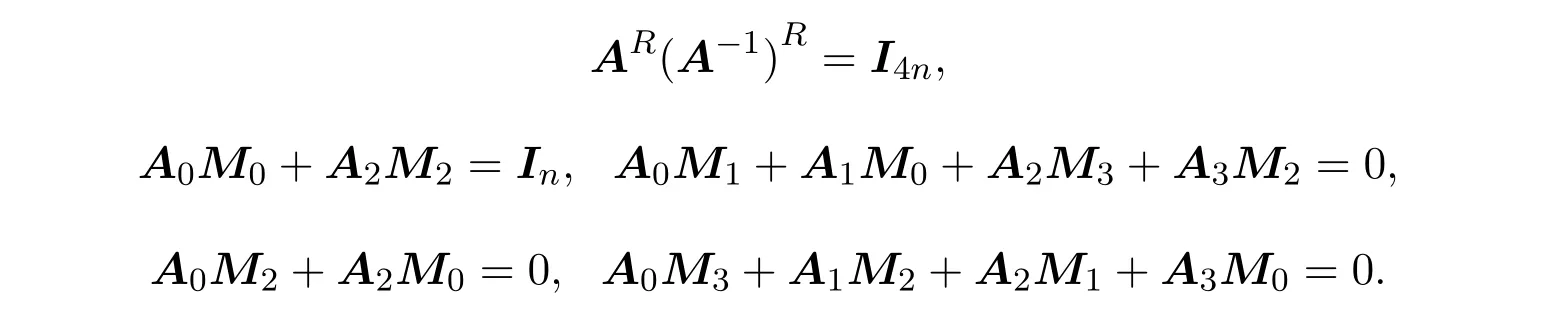
取

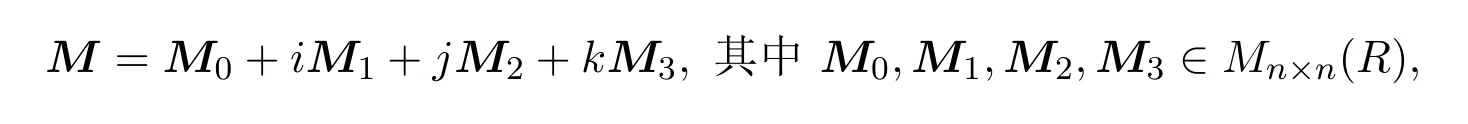
则

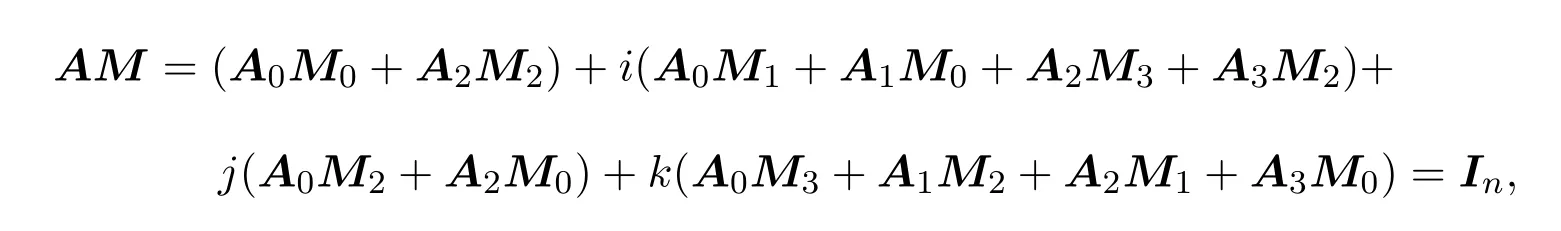
由定理5.1知,

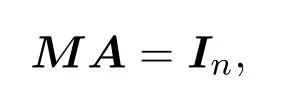
故

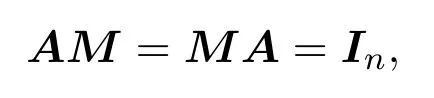
则

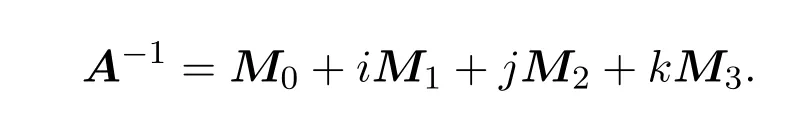
注 5.1定理5.2给出了求抛物型交换四元数矩阵A的逆矩阵的方法.具体可总结为以下几步:

①写出A的实表示AR;②求出AR的逆矩阵(AR)−1;③令

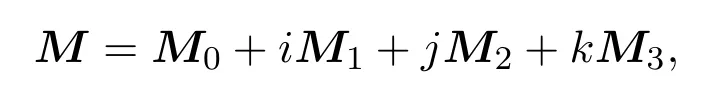
则

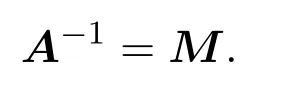
该方法使得利用计算机求抛物型交换四元数矩阵的逆矩阵成为可能.

6 算例

设

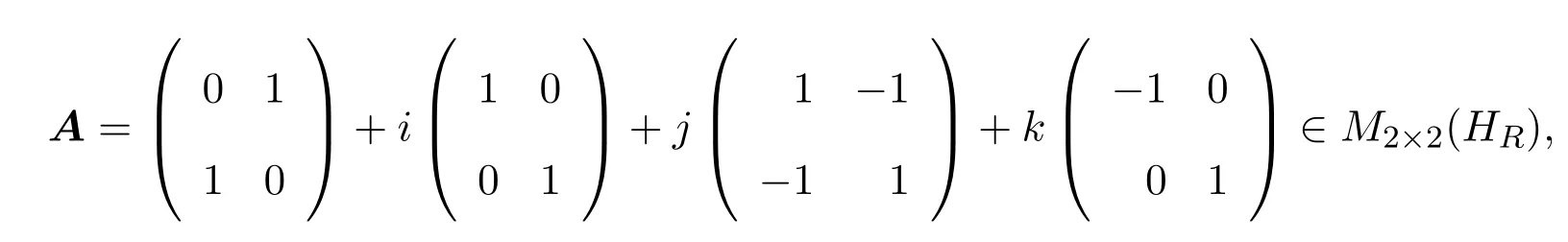
则

求得

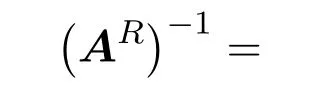
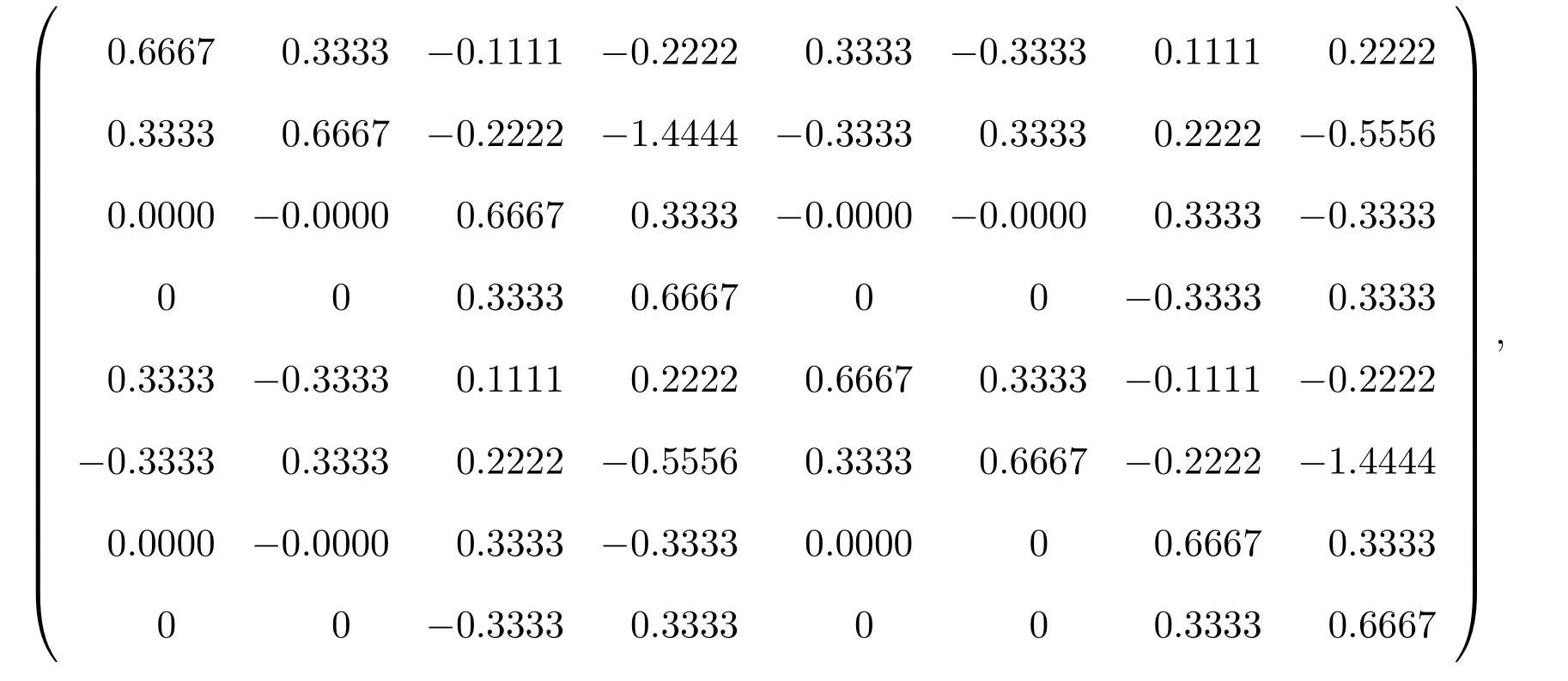
所以

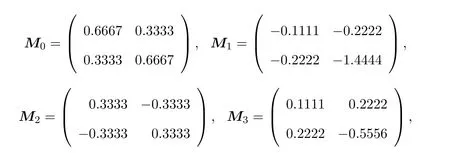
故

经检验所得结论正确.

7 结语

本文推导了抛物型交换四元数及其矩阵的重要性质;通过抛物型交换四元数矩阵的实表示,得到求该类矩阵逆矩阵的新方法,为进一步研究抛物型交换四元数矩阵的行列式问题、可对角化问题,及特征值等问题提供了重要理论支撑.对交换四元数及交换四元数矩阵的研究已逐渐成为四元数研究领域的热点问题.另外,在本文的基础上,还可展开对其他类型交换四元数及其矩阵性质的研究.

[1]Alagoz Y,Oral K H,Yuce S.Split quaternion matrices[J].Miskolc Math.Notes,2012,13(2):223-232.

[2]Pogoruy A,Rodriguez Dagnino R M.Some algebraic and analytical properties of coquaternion algebra[J].Adv.Appl.Cli ff ord Algebra,2010,20(1):79-84.

[3]Ozdemir M.The roots of split quaternion[J].Appl.Math.Lette.,2009,22(2):258-263.

[4]Kula L,Yayli Y.Split quaternions and rotations in semi Euclidean space[J].J.Korean Math.Soc.,2007,44(6):1313-1327.

[5]Ozdemir M.On complex split quqternion matrices[J].Adv.Appl.Cli ff ord Algebra,2013,23(3):625-638.

[6]Ozdemir M.On eigenvalues of split quaternion matrix[J].Adv.Appl.Cli ff ord Algebra,2013,23(3):615-623.

[7]Segre C.The real representations of complex elements and extension to bicomplex systems[J].Math.Ann.,1892,40:413-467.

[8]Pinotsis D A.Segre Quaternions,Spectral Analysis and a Four-Dimensional Laplace Equation,in Progress in Analysis and Its Applications[M].Singapore:World Scienti fic,2010.

[9]Catoni F,Cannata R,Nichelatti E,et al.Commutative hypercomplex numbers and functions of hypercomplex variable:a matrix study[J].Adv.Appl.Cli ff ord Algebra,2005,15(2):183-213.

[10]Pei Soochang,Chang Jahan,Ding Jianjiun.Commutative reduced biquaternions and their fourier transform for signal and image processing applications[J].IEEE Transactions on Sinal Processing,2004,52(7):2012-2031.

[11]Catoni F,Cannata R,Zampetti P.An introduction to commutative quaternions[J].Adv.Appl.Cli ff ord Algebra,2006,16(1):1-28.

[12]Kosal H H,Tosun M.Commutative quaternion matrices[J].Adv.Appl.Cli ff ord Algebra,2014,16(3):769-799.