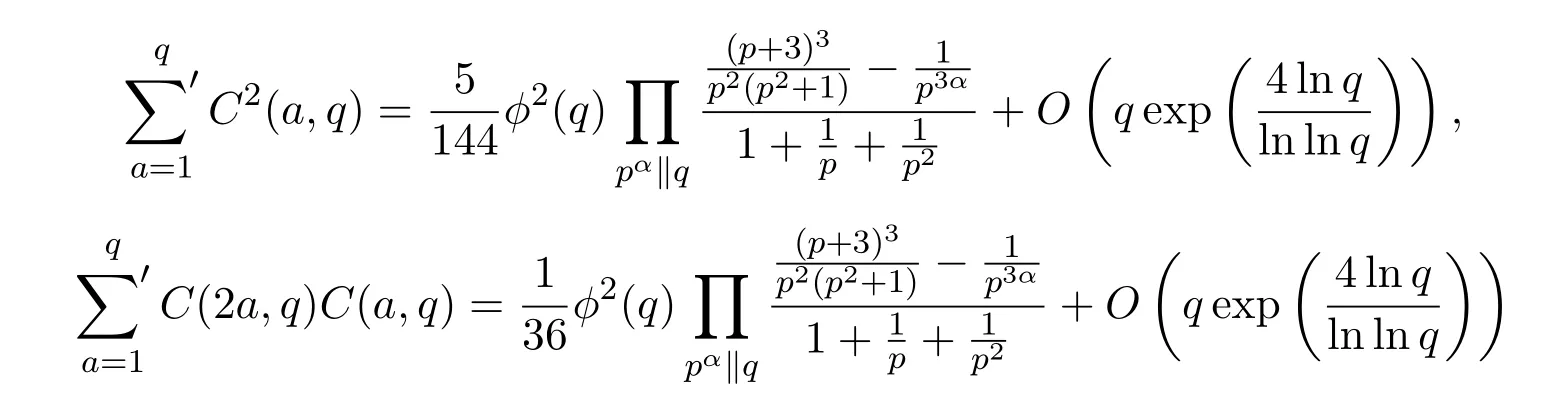一个类Lehmer问题误差项的均值估计
2018-06-23田清丁丽萍
田清,丁丽萍
(西安建筑科技大学理学院,陕西 西安 710055)
1 引言
设奇数q>2,整数a与q互素,对任何满足条件1≤b 这里表示所有与q互素的b求和.不难看出M(a,q)即表示同余方程 满足条件1≤b,c 这里ϕ(q)为欧拉函数,d(q)为除数函数.不仅如此,文献[3]还定义了误差项 并利用Dedekind和与Cochrane和的性质给出了 这里表示q的所有素因子p的乘积,满足pα|q且pα+1†q. 引入类Lehmer问题如下:设奇数q>2,整数a与q互素,N(a,q)表示同余式 并且c和奇偶性不同的解b,c的个数.对于这个问题的研究是非常有意义的,因为对Lehmer问题一系列的研究方法和成果在伪随机数列的构造中发挥重要作用[4].而类Lehmer问题似乎比Lehmer问题更加复杂,以至于我们至今都没有找到获得类Lehmer问题误差项 一次均值的有效方法.为此,本文将利用Cochrane[5-8] 的性质给出E(a,q)的平均阶估计及一次混合均值,即得到如下两个定理. 定理 1.1设任意奇数q>2,整数a与q互素,有 这里ε是小于1的正数,≍表示两侧函数平均阶相同. 定理 1.2设任意奇数q>2,有渐近公式 为证明定理,首先引入下面几个引理. 引理 2.1[9]设奇数q>2,χ是模为q的特征,则有恒等式 引理 2.2设奇数q>2,整数a与q互素,有恒等式 证明由N(a,q)的定义及特征的正交性质可得 如果χ(−1)=1,有 而如果χ(−1)=−1,则有 结合引理2.1及(1),(2)和 (3)式,可得 于是完成了引理2.2的证明. 引理 2.3设奇数q>2,整数a与q互素,χ是模为q的特征,则有 和 证明证明方法类似文献[3]中引理1. 结合上述引理,给出定理的证明: 定理 1.1的证明由引理2.2和引理2.3可得 又由参考文献[3]可知 由此可得 定理1.1证明完毕. 下面给出定理1.2的证明. 定理 1.2的证明同样由引理2.2和引理2.3得 另一方面,利用参考文献[3]中的方法可以得到 和 将此代入(4)式即可得 定理1.2证明完毕. 本文利用解析方法研究了一个类Lehmer问题的误差项均值估计问题,给出了它的平均阶估计和一个一次混合均值的渐近公式.能否得到其它与Lehmer问题类似的结果,还有待于进一步研究. [1]Richard K G.Unsolved Problems in Number Theory[M].New York:Springer Verlag,1994. [2]Zhang Wenpeng.On the di ff erence between a D.H.Lehmer number and its inverse moduloq[J].Acta Arithmetica,1994,29:255-263. [3]Zhang Wenpeng,Xu Zongben,Yi Yuan.A problem of D.H.Lehmer and its mean square value formula[J].Journal of Number Theory,2003,103:197-213. [4]Liu Huaning.New pseudorandom sequences constructed by quadratic residues and Lehmer numbers[J].Proceedings of the American Mathematical Society,2007,135:1309-1318. [5]Zhang Wenpeng.On a Cochrane sum and its hybrid mean value formula[J].Journal of Mathematical Analysis and Application,2002,267:89-96. [6]Zhang Wenpeng.On a Cochrane sum and its hybrid mean value formula(II)[J].Journal of Mathematical Analysis and Application,2002,276:446-457 [7]Xu Zongben.A mean value of Cochrane sum[J].Acta Mathematica Sinica,2009,25(2):223-234. [8]白文,任刚练.关于广义齐性Cochrane和的加权均值[J].纯粹数学与应用数学,2013,29(2):910-196. [9]徐哲峰,张文鹏.Dirichlet函数及其应用[M].北京:科学出版社,2008.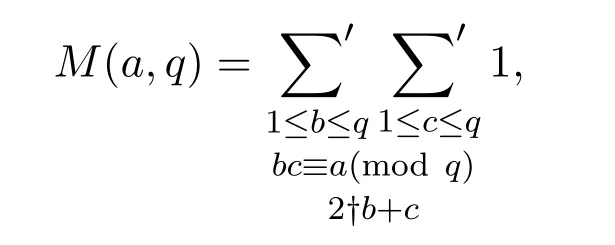


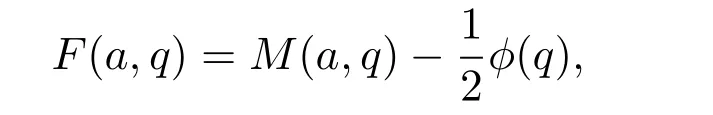
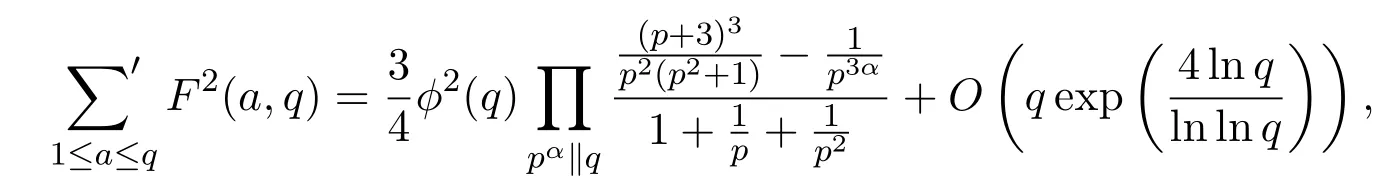

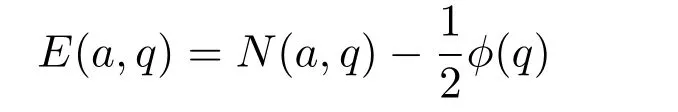
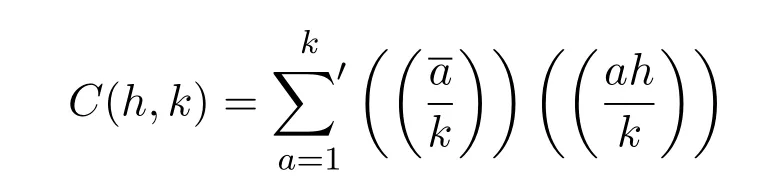


2 几个引理

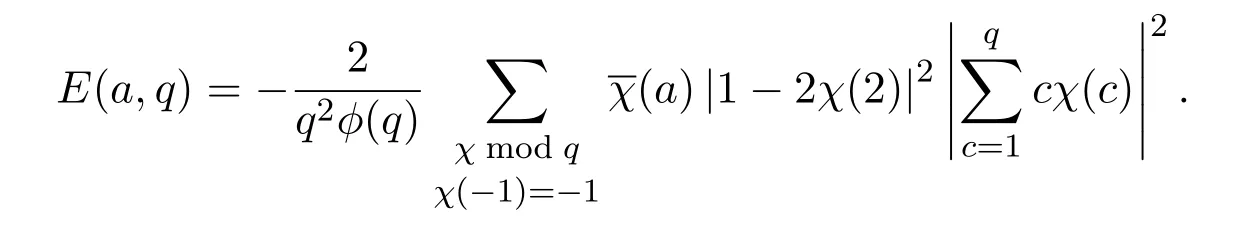





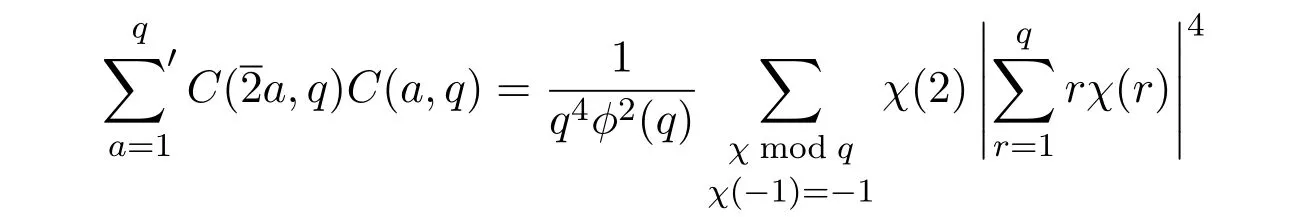

3 定理证明