考虑剪切效应的复合材料层合板阻尼特性研究

王文博，漆文凯，沈 承

（南京航空航天大学江苏省航空动力系统重点实验室，南京210016）

0 引言

先进的复合材料作为当前最具研究前景的新型战略材料被广泛应用于航空航天结构件上。复合材料与传统广义上的混合材料的本质区别在于采用复杂的复合工艺从微观层次上将不同材料进行搭配组合，使得各基础材料性能的不足得以互相弥补。这种制造工艺决定了复合材料具有灵活的可设计性优点，可以通过材料设计使各材料在性能上产生预期的相互协同效应，从而获得理想的抗疲劳、耐腐蚀、高强度质量比的新型复合材料，满足航空发动机复杂外部环境的需求。因此复合材料成为现阶段航空发动机结构设计中最重要的先进材料之一[1-4]，应用于风扇叶片、导流板、降噪蜂窝内衬以及外涵机匣等航空发动机冷端部件。与传统钛合金相比，航空发动机结构中应用先进复合材料的减质效果明显。据美国NASA统计，减质比可达13.1%。然而在使用先进复合材料进行部件结构设计时，材料的阻尼特性预测比传统钛合金复杂得多。有关复合材料层合板的研究显示，复合层数、各层铺设角度、各层厚度与其阻尼特性有着直接联系，因此预测和分析在复杂的外部载荷下复合材料的阻尼特性是结构设计师最关心的问题之一。国内外学者[5-11]对此做了大量研究工作，总结了先进复合材料结构的阻尼表现机理，有纤维和基体固有的黏弹性阻尼、复合材料界面相阻尼、复合材料损伤的耗散阻尼等。

在工程应用中，对于板壳结构的处理方法有Kirchhoff假设和Hencky假设，后者相对于前者考虑了剪切变形的影响。上述研究工作中的复合材料模型大多基于Kirchhoff板壳假设，未考虑剪切应力对有限元模型的影响。研究表明，剪切变形对复合材料层合板结构的阻尼特性影响显著，而且影响效果随着板的厚度增加而增强。本文引入Hencky[12-13]假设在剪切应力的影响下，建立了复合材料层合板的有限元分析模型，该模型可广泛适用于薄板和中厚板。本文利用Matlab软件对上述模型理论进行了计算，通过算例验证了等效损耗因子预测模型，最后具体分析了矩形层合板结构的长宽比对固有频率和振型的影响规律。

1 有限元模型

有限元分析关键在于计算工程结构的刚度矩阵[K]

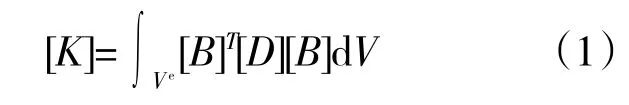
式中：上标e代表单元，V代表单元的体积；[B]为几何矩阵，[D]为刚度系数矩阵，分别反映了单元内部的应变-位移关系和应变-应力关系。

1.1几何矩阵

如图1所示，基于Hencky假设下，板上任意1点的位移函数为

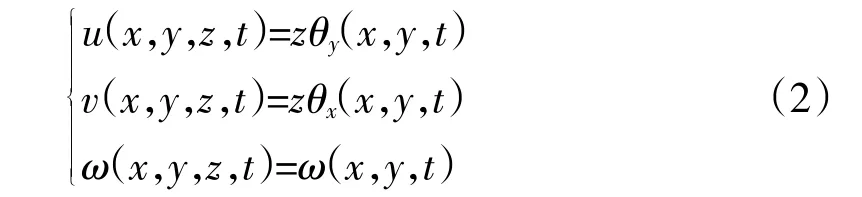
式中：θy（x,y）和θx（x,y,t）为中间层平面的转动角度。

图1 考虑剪切影响时转角与位移关系

此时，应变矩阵ε表示为

式中：{δ}e为单元的结点位移值；[B]为几何矩阵，二者详细表示如下

中面为平面曲边四边形的8结点板单元如图2所示。其中面形状和厚度描述为

图2 8结点Hencky板单元

8结点Hencky板壳壳单元的形函数为

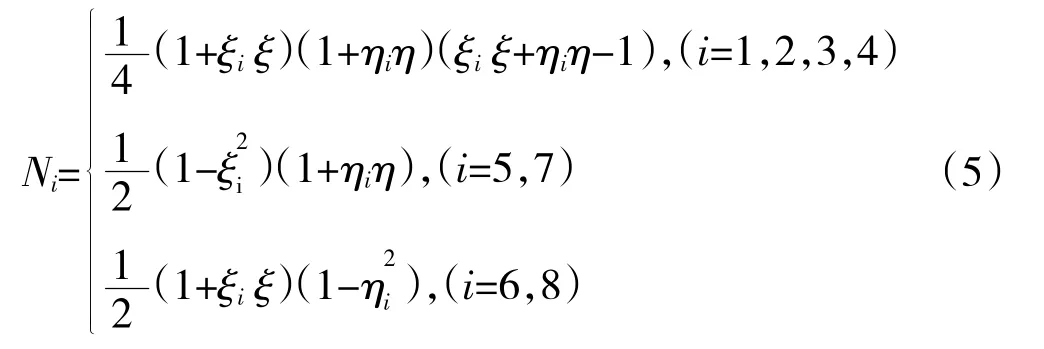
式中：Ni（ξ，η）为局部坐标的插值函数。

而[B]矩阵要求对整体坐标进行求导，坐标转换有

式中：[J]为雅可比矩阵，阶次为2×2。

结合式（2）～（5），可写出任意位置点i（ξ，η）的形函数Ni，根据式（6）计算形函数Ni对坐标x，y的1阶偏导数。

1.2 等效刚度矩阵

假设材料表现为正交各向异性，各层的应力与应变关系为

式中：[Q]为刚度相关矩阵，各非零元素为

式中：E1、E2分别为材料在 0°、90°方向的杨氏模量；ν为材料的泊松比。

为了体现各层的铺层方向，在微观层次下统一复合材料纤维的坐标系统，如图3所示。此时单层结构主轴方向1-2与x-y坐标之间的夹角为θk（k=1，2，…，n）。引入坐标转换公式

图3 局部坐标与整体坐标的几何关系

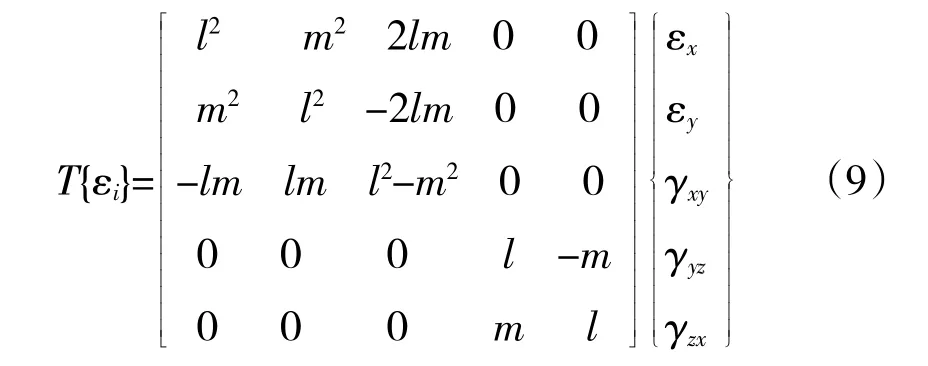
其中l=cosθ，m=sinθ。

于是，任意θ角方向刚度矩阵可以表示为

N层结构的层合板总应变能可写成

式中：Ω为待积分平面；hk和hk-1为第k层板的上、下面的坐标值。

将式（3）代入式（11）中，计算层合板刚度系数矩阵

1.3 特征方程

层合板系统内部的总应变能为

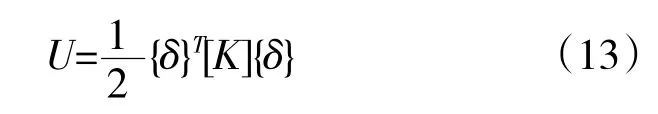
式中：{δ}为节点位移。

类似地，层合板总动能可表示为

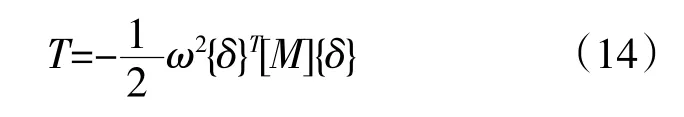
式中：[M]为总质量矩阵；ω为角频率。

根据最小势能原理

得到标准特征方程

通过式（16）可以求得各特征值ωr以及相对应的各模态振型δr。

2 比阻尼容量

计算系统的耗散能量ΔU与系统的最大应变能U的比值，将上述比值定义为1个周期内的比阻尼容量φSDC，即

经过调研，由于教师薪酬、院校办学经费等原因，吉林省高职院校旅游管理专业的核心课程教学任务基本上都是由本校教师承担，即使外聘教师，通常也对其学历及职称有要求，这就极大限制了旅游企业在一线实践技能高超的人员走进大学课堂。在师资引进时，各院校对应聘者学历要求是首要考虑的因素，以旅游管理专业博士研究生为主、硕士研究生为辅。从教育规律来看，硕士、博士阶段是以培养科研型人才为主，因此，进入高职院校从事教学活动的教师通常具有极高的科研能力，但是大多没有旅游企业实践经历，其实践技能相对匮乏，这就与高职院校培养高技能应用型人才产生了矛盾。

在此基础上，假设系统结构中的耗散能量ΔU等于各方向应力产生耗散能量之和

或者简化成

式中：ψij为上述各向的损耗因子。

本文通过对三相桥联模型[14]等效方法进行改进求得，式（18）可以整理为

求解等效阻尼刚度系数矩阵Dd与D类似，将式（12）中替换成如式（21）所示。

层合板系统的耗散能ΔU表示为

任意阶模态振型δr可通过式（16）得到，最大应变能U和耗散能量ΔU可以根据式（13）、（22）得到。将U和ΔU代入式（17）得到各阶比阻尼容量φr。

3 模型验证

本文基于Hencky理论假设，建立了8结点四边形板壳单元模型，对其各阶固有频率进行预测，并利用能量法求解各阶模态比阻尼容量。约束条件为一端固支的情况。为了验证有限元模型的有效性，首先将计算结果与文献[15]中瑞利-里兹法的理论值和试验结果进行比较。

目标复合材料913C-TS与913C-HTA的材料参数见表1。

表1 目标复合材料属性参数

目标复合材料层合板材料参数详见文献[15]，对结果进行比较见表2、3。

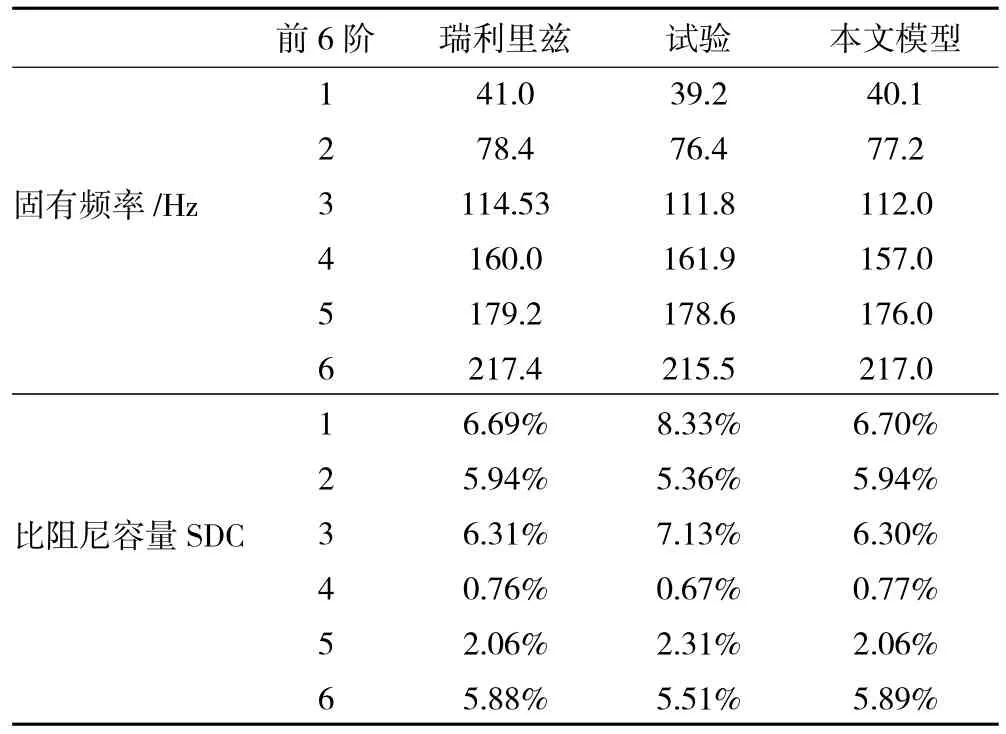
表2 层合板材料913C-TS参数

从表中可见，在2种材料和铺层设置情况下，无论是固有频率或者比阻尼容量，本文提出的改进模型的预测结果与瑞利-里兹法解析以及文献[15]中试验结果吻合性良好，初步说明了改进模型的有效性，在原有研究基础上考虑了剪切效应的影响，可进一步用于试验测试验证及参数讨论，对碳纤维复合材料层合板等效损耗因子的研究提供了新方法，在其阻尼特性研究上具有较高的参考价值。总的来说，固有频率各结果之间的误差基本小于比阻尼容量之间的误差，侧面反映了阻尼机理的复杂性以及难以预测性。

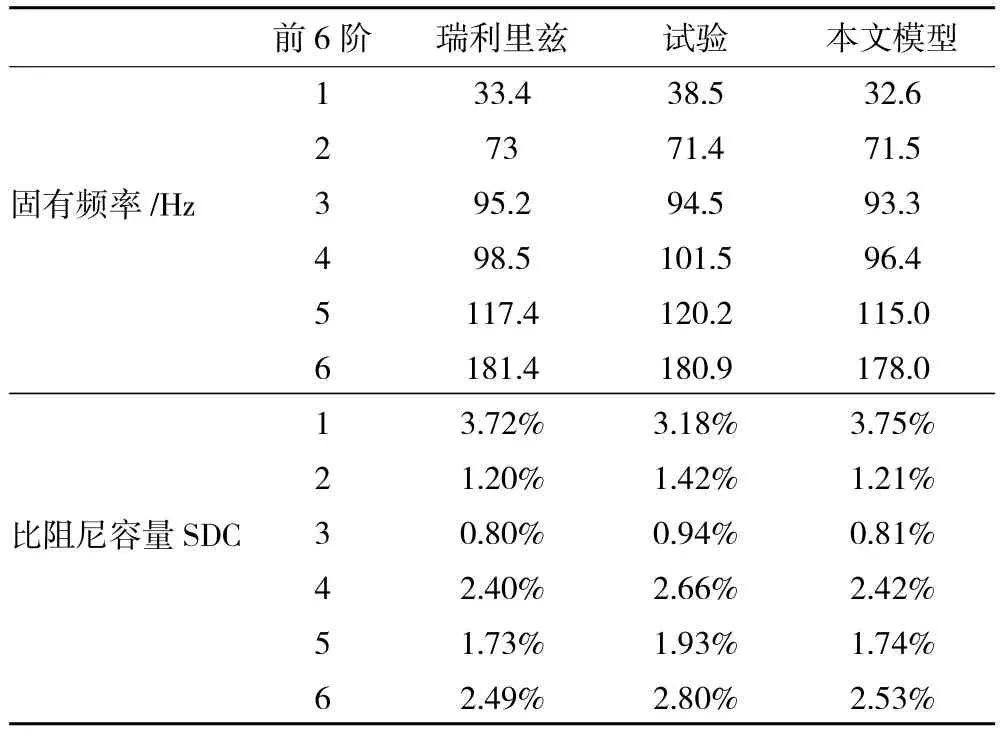
表3 层合板材料913C-HTA 参数

4 参数讨论

根据本文建立的Hencky理论有限元模型详细讨论复合材料层合板的结构几何参数（主要是边长）对前6阶固有频率的影响，如图4、5所示。

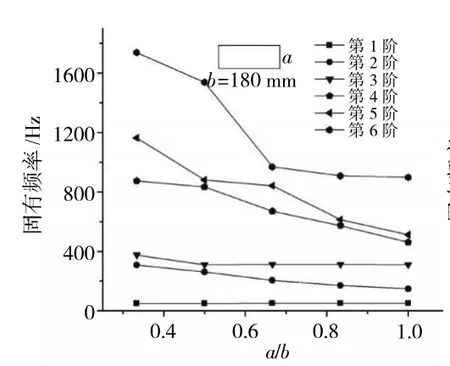
图4 边长a对固有频率的影响（T300/BMP316）

图5 边长b对固有频率的影响（T300/BMP316）

从图4中可见，第1、3阶固有频率变化幅度微小，其振型分别表现为1阶弯曲和2阶弯曲，说明层合板弯曲变形受宽度a变化影响很小；第6阶固有频率在各阶段的幅度变化程度不同，当边长比值在0.6附近时，第6阶固有频率幅度变化最为显著，而比值达到0.7时，第6阶固有频率变化幅度趋于平缓；（3）第4、5阶固有频率均随宽度a的增加呈近似线性降低，且各阶频率接近。

从图5中可见，第1、2阶固有频率表现平缓，第3～5阶固有频率均随长度减小呈一定比例线性提高，且第4、5阶固有频率变化十分接近，而第6阶固有频率受长度变化的影响同样是最为显著。

综上所述，第1阶固有频率受层合板结构的长宽比影响微小，第2～5阶频率轨迹大多呈近似线性变化，而第6阶固有频率受长宽比变化影响最大。从层合板结构几何参数上详细分析了长宽比对结构各阶模态特性的影响，对结构部件抗振优化设计有一定参考价值。

5 总结

本文应用Hencky假设，考虑剪切效应，建立了复合材料层合板结构的有限元模型，通过推导层合板总刚度、质量、阻尼矩阵，引入了耗散能原理，求解了目标算例复合材料层合板的前6阶模态及相应的比阻尼容量。将结果与现有文献的理论解进行对比，初步验证了本文改进模型的有效性，并结合试验结果进一步说明模型的准确性。

研究表明：复合材料层合板在一端固支下，无论是长度还是宽度的变化，对第1阶固有频率的影响都很微弱，而第4、5阶固有频率表现出趋于同频现象，振型也会产生类似变化趋势。而在长度和宽度变化下，第6阶模态结果则表现出相反的对数变化轨迹。

[1]SHEN Cheng，XIN Fengxian，CHENG Li，et al.Sound radiation of orthogonally stiffened laminated composite plates under airborne and structure borne excitations[J].Composites Science and Technology，2013，84：51-57.

[2]陈祥宝.聚合物基复合材料手册[M].北京：化学工业出版社，2004：1-3.CHEN Xiangbao.Handbook of polymer matrix composites[M].Beijing：Chemical Industry Press，2004：1-3.（in Chinese）

[3]陈绍杰.复合材料技术与大型飞机 [J].航空学报，2008，29（3）：605-610.CHEN Shaojie.Composite technology and large aircraft[J].Acta Aeronautica et Astro-nautica Sinica，2008，29（3）：605-610.（in Chinese）

[4]杜善义.先进复合材料与航空航天 [J].复合材料学报，2007，24（1）：1-12.DU Shanyi.Advanced composite materials and aerospace[J].Acta Materiae Compositae Sinica，2007，24（1）：1-12.（in Chinese）

[5]Adams R D，Bacon D G C.Measurement of the flexural damping capacity and dynamic Young's modulus of metals and reinforced plastics[J].Journal of Physics D：Applied Physics，1973，6（1）：27.

[6]Mahi A E，Assarar M，Sefrani Y，et al.Damping analysis of orthotropic composite materials and laminates[J].Composites Part B：Engineering，2008，39（7）：1069-1076.

[7]Berthelot J M，Assarar M，Sefrani Y，et al.Damping analysis of composite materials and structures[J].Composite Structures，2008，85（3）：189-204.

[8]Kameyama M，Arai M.Optimal design of symmetrically laminated plates for damping characteristics using lamination parameters[J].Composite Structures，2015，132：885-897.

[9]尤凤翔，吕福和.复合材料层合板力学性质分析及角铺设层优化设计[J].噪声与振动控制，2009，29（4）：138-143.YOU Fengxiang，LYU Fuhe.Analysis of mechanics properties of composite laminated plates and optimization of angle arrangement of plies[J].Noise Vibration and Control，2009，29（4）：138-143.（in Chinese）

[10]漆文凯，程博.复合材料层合板阻尼预测分析与验证[J].振动.测试与诊断，2013，33（6）：1049-1053.QI Wenkai，CHENG Bo.Analysis and verification of damping prediction of composite laminated plates[J].Vibration Measurement and Diagnosis，2013，33（6）：1049-1053.（in Chinese）

[11]杨雪，王源升，朱金华，等.多层阻尼复合结构阻尼性能[J].复合材料学报，2005，22（3）：175-181.YANG Xue，WANG Yuansheng，ZHU Jinhua，et al.Damping properties of the composite structures with multilayered damping materials[J].Acta Materiae Compositae Sinica，2005，22（3）：175-181.（in Chinese）

[12]曾维栋.Reissner-Mindlin板壳无网格法研究及形状优化[D].湖南湘潭：湘潭大学，2009.ZENG weidong.Research on Reissner-Mindlin plate shell meshless method and shape optimization[D].Hunan Xiangtan：Xiangtan University，2009.（in Chinese）

[13]王焕定，陈少峰，边文凤.有限单元法基础及Matlab编程[M].北京：高等教育出版社，2012：362-364.WANG Huanding，CHEN Shaofeng，BIAN Wenfeng.Fundamentals of finite element method and matlab programming[M].Beijing：Higher Education Press，2012：362-364.（in Chinese）

[14]Qi Wenkai，Xu Xiaoqiang.Analytical method of dynamical properties of FRP based on micromechanical level[J].Chinese Journal of Aeronautics，2015，28（3）：939-945.

[15]Maheri M R，Adams R D.Modal vibration damping of anisotropic FRP laminates using the Rayleigh-Ritz energy minimization scheme[J].Journal of Sound and Vibration，2003，259（1）：17-29.