航迹可编程飞行器航程计算方法*
2018-06-22杨华东庹红平
杨华东,庹红平
(1.海军工程大学,湖北 武汉 430033;2. 海军研究院,北京 100161;3.北京机电工程总体设计部,北京 100143)
0 引言
航程是各类飞行器重要的飞行控制诸元参数。特别是制导武器,精确的航程计算,贯穿武器导航和制导的各个环节:发射前,需要精确估算全航线航程,以便计算武器的飞行时间、机动突防距离等战术参量;飞行中,导航系统必须实时精确的计算当前飞行航程,才能保证武器导航参数和制导控制参数的正确性和时效性。
国内外学者对航行器/飞行器航程计算方法的研究多集中于舰船和飞机等对象[1-7],关注的重点在于地球椭球面上大地线长度的优化计算。文献[8-9]和文献[10]分别研究了反潜自导鱼雷和UAV在不同航速下的航程计算方法,其应用范围仅限于不具备航路规划能力的直航式武器。文献[11-12]在高超声速飞行器纵向航迹规划中提出了航程与速度的关系式,并提出了可用剩余航程的校正方法。文献[13-14]分析了电池容量和燃料消耗对无人飞行器航程的影响,给出了推进系统额定功率下的航程估计方法。从公开的文献资料来看,国内外对具有可编程能力的制导飞行器航迹计算方法的研究还很少见。本文研究了航迹可编程飞行器的航程计算方法,涵盖从飞行器发射起飞、扇面转弯、巡航飞行等全航段的航程精确计算。
1 起飞初段航程计算
1.1 水平面内航程计算
制导武器发射后的弹道轨迹如图1所示:武器发射起飞后,通常沿发射方向在垂直平面内开始按程序爬升,待爬升一段距离、飞行速度和姿态满足控制要求后,即可在水平面内进行扇面转弯,同时保持垂直面内继续爬升,抵达设定弹道高度后,即开始按程序下滑。当下滑至设定高度,即在既定高度保持机动飞行,直至抵达目标。
为了计算飞行器起飞后水平面内扇面转弯段的航迹,本文首先给出了飞行器扇面转弯弧线圆心的计算方法, 然后给出了弧线段航迹计算方法。
解决水平面内飞行器起飞初段航迹计算问题所采用的技术方案如图2所示。
O点为起飞点位置,A点为飞行器扇面转弯开始点,|OA|为飞行器起飞后沿初始起飞方向的飞行距离,值为常数。T点为扇面转弯结束点;N1为第一个航路转弯点;Q0点为扇面转弯圆心,转弯半径|AQ0|,|TQ0|为常数R0,满足:Q0A⊥OA,Q0T⊥TN1。
求解飞行器初段扇面转弯航迹,关键是要求解出扇面转弯圆心角∠AQ0T,记θ=∠AQ0T。
由于飞行器起飞点位置和起飞初始航向是已知的,于是A点的位置很容易求得。
在△OAQ0中:
(1)
(2)
由于起飞点位置坐标和初始航向已知,联立式(1)和式(2),采用大地主题正解公式[15]容易求得Q0点位置坐标。
在△AQ0N1中,由于A点、Q0点和N1点的位置已知,采用大地主题反解公式[15],容易计算得到|AN1|,由余弦定理,求得∠AN1Q0为
(3)
在△TN1Q0中:
(4)
在△ATQ0中:
(5)
(6)
在△ATN1中:
∠ATN1=∠ATQ0+90°,
(7)
∠TN1A=∠TN1Q0-∠AN1Q0.
(8)
A点和N1点位置已知,由大地主题反解公式,易求得|AN1|,由正弦定理有
(9)
将式(3)~(8)代入式(9),可得
(10)
解此方程,可求得飞行器初段扇面转弯圆心角θ,于是,在△ATQ0中,由大地主题正解公式,易求得T点位置坐标。
于是,飞行器自起飞、开始扇面转弯到扇面转弯结束点T的水平面内航程即为
S0=|OA|+R0θ.
(11)
1.2 垂直面内航程计算
如图1所示,制导武器起飞后,在垂直面内爬升并同时在水平面内扇面转弯,爬升到设定高度,然后通常按程序下滑至巡飞高度,对航迹可编程飞行器,为了满足飞行航路避障需要或特定攻击方向进入的需要,可在水平面内机动飞行,如图3所示。
飞行器在高度为h的D点开始下降高度,按设定程序下滑至下滑轨迹结束点N1。
记Rzw为飞行器从无动力下滑段,与飞行器下滑高度的函数关系为
Rzw=f(h)=a0+a1h-a2h2+
a3h3-a4h4+a5h5,
(12)
式中:a1,a2,a3,a4,a5为拟合常数,根据试验或仿真数据确定。Rzw,h的单位为km。
2 巡航段航程计算
飞行器完成下滑后,即转入巡航段飞行。具有航迹可编程能力的巡航飞行器,航路上可设置多个航路点。为了计算飞行器转平飞后巡航段航程,本文给出了根据飞行器航路特征点(航路点)和飞行器转弯半径R计算平飞段和曲线转弯段航程的方法。
考虑到飞行器航路一般具有2~N个航路点,本文分2个航路点、3个航路点、4个航路点和5个航路点共4种情况讨论计算巡航段航程,并进一步推广到任意N(N>2)个航路点的情况。
2.1 2个航路点情况
2个航路点情况如图4所示。
图4中,N1点为飞行器由下滑段转巡航平飞段起点,M为目的地点。
此时航路无转弯点,飞行器无动力下滑段结束后直接对准目标M,巡航段航程L1满足:
L1=|N1M|.
(13)
则总航程S由式(14)计算:
S=S0+Rzw+L1.
(14)
2.2 3个航路点情况
考虑3个航路点情况,如图5所示。
N1,N2为规划的航路点;O点为航路转弯圆心;M点为目的地点;R为航路转弯半径,取常值。
由O点分别向N1N2和N1M引垂线,垂足D1,D2分别为航路转弯起点和终点;θ1为航路转弯圆心角。
此时航路有1个航路转弯点N2,飞行器无动力下滑段结束后对准航路转弯点N2。飞行器完成航路转弯后对准目标点M。
巡航段航程L2满足:
(15)
如图5所示,由于N1,N2和M3个点位置已知,求解△N1N2M,容易求得飞行器航路转弯角∠N1N2M,则飞行器转弯轨迹圆心角为
θ1=180°-∠N1N2M.
(16)
飞行器转弯半径为R,则3航路点巡航段航程为
(17)
则总航程为
S=S0+Rzw+L2.
(18)
2.3 4个航路点情况
考虑4个航路点情况,如图6所示。
图6中,N1,N2,N3为规划的航路点;M为目标点;O1,O2为航路转弯圆心;R为航路转弯半径。
由O1点分别向N1N2和N2N3引垂线,垂足D1,D2分别为航路转弯起点和终点;由O2点分别向N2N3和N2M引垂线,垂足D3,D4分别为航路转弯起点和终点;
θ1,θ2为航路转弯圆心角。
则,巡航段航程L3满足:
(19)
由图6,易求得飞行器航路转弯角∠N1N2N3,∠N2N3M,则飞行器转弯轨迹圆心角为
θ1=180°-∠N1N2N3,
(20)
θ2=180°-∠N2N3M.
(21)
飞行器转弯半径为R,则4航路点巡航段航程为
L3= |N1N2|+|N2N3|+|N3M|+(Rθ1-
(22)
总航程S由式(23)计算:
S=S0+Rzw+L3.
(23)
2.4 5个航路点情况
考虑5个航路点情况,如图7所示。
图7中,N1,N2,N3,N4为规划的航路点;M为目的地点;O1,O2,O3,为航路转弯圆心;R为航路转弯半径。
由O1点分别向N1N2和N2N3引垂线,垂足D0,D1分别为航路转弯起点和终点,由O2点分别向N2N3和N3N4引垂线,垂足D2,D3分别为航路转弯起点和终点;由O3点分别向N3N4和N4M引垂线,垂足D4,D5分别为航路转弯起点和终点;
θ1,θ2,θ3为航路转弯圆心角。
则,巡航段航程L4满足:
(24)
由图7,易求得飞行器转弯角∠N1N2N3,∠N2N3N4,∠N3N4M,则飞行器转弯轨迹圆心角为
θ1=180°-∠N1N2N3,
θ2=180°-∠N2N3N4,
θ3=180°-∠N3N4M.
飞行器转弯半径为R,则5个航路点巡航段航程为
L4= |N1N2|+|N2N3|+|N3N4|+|N4M|+(Rθ1-
(25)
总航程为
S=S0+Rzw+L4.
(26)
2.5 推广N个航路点情况
推广到N个航路点的情况。
由2个航路点、3个航路点、4个航路点、5个航路点的情况下巡航段航程Li(i=1,2,3,4)计算公式,可推广到N个航路点巡航段航程Ln为
Ln= |N1N2|+|N2N3|+|Nn-2Nn-1|+…+
(27)
N个航路点时,总航程为
S=S0+Rzw+Ln
(28)
3 仿真验证
为了检验本文所提出的各种情况下飞行器航程计算方法的正确性和计算精确性,分别取扇面角Ψ=0°,Ψ=90°条件下,航路点个数分别为N=2,N=3,N=4,N=5时,采用本文方法计算的飞行器航程理论值与飞行试验中飞行器携带的导航系统实际测量值进行了比对,如表1所示。
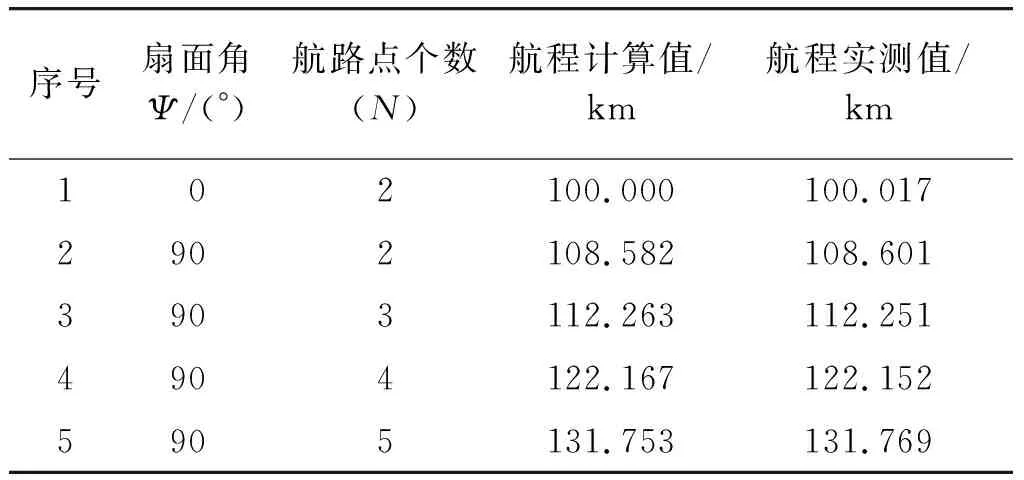
表1 计算结果与试验结果比较
由表1可见,采用本文方法计算的航程与飞行器导航系统实际测量值之间的误差最大不超过20 m,具有计算精度较高的特点,能够满足航迹可编程飞行器导航与制导的控制要求。
此外,由于本文所提出的航程计算公式,均是基于解析几何的数学方法,有唯一解,且无迭代计算,具有支持快速计算的特点,非常适于弹载或机载综合控制计算机飞行中在线航程计算。
4 结束语
本文研究了具有低空巡航特点的飞行器从起飞至到达目的地全程的航程精确计算方法,具有计算速度快、精度高的特点,可广泛用于快速计算具有航迹编程能力的制导飞行器从地面起飞或从空中投放后,沿规划的航路抵达目标的精确航程。
参考文献:
[1] 李厚朴,王瑞.大椭圆航法及其导航参数计算[J].海军工程大学学报,2009,21(4):7-12.
LI Hou-pu,WANG Rui.Great Ellipse Nautical Method and Its Navigation Parameters Calculation [J].Journal of Naval University of Engineering,2009,21(4):7-12.
[2] 刘文超,卞鸿巍,王荣颖,等.大椭圆航线设计的空间矢量方法[J].测绘学报,2015,44(7):741-746.
LIU Wen-chao,BIAN Hong-wei,WANG Rong-ying,et al.Great Ellipse Route Planning Based Space Vector [J].Acta Geodaetica et Cartographica Sinica,2015,44(7):741-746.
[3] 胡江强,杨盐生,李铁山.恒向线航向和航程的精确计算[J].大连海事大学学报,2005,5(2):11-14.
HU Jiang-qiang,YANG Yan-sheng,LI Tie-shan.Accurate Caculation of the Course and Distance in Rhumb Line[J].Journal of Dalian Maritime University,2005,5(2):11-14.
[4] 蔡开龙,谢寿生.基于最小二乘拟合法的某型飞机航程计算的实现[J].航空计算技术,2003,33(1):4-7.
CAI Kai-long,XIE Shou-sheng.Flying Distance’s Computation of X Aeroplane Based on Least Square Method[J].Aeronautical Computer Technique,2003,33(1):4-7.
[5] 孙春亚,宋保维,王鹏.翼身融合水下滑翔机外形优化设计[J].水下无人系统学报,2017,25(1):68-76.
SUN Chun-ya,SONG Bao-wei,WANG Peng.Shape Optimization of Blended-Wing-Body Underwater Glider [J].Journal of Unmanned Undersea System,2017,25(1):68-76.
[6] 赵战兴.最小二乘法分段在船舶航迹拟合研究中的应用[J].舰船科学技术,2016,38(3A):27-30.
ZHAO Zhan-xing.Application of the Least Square Method in the Research of Ship Track Fitting[J].Ship Science and Technology,2016,38(3A):27-30.
[7] 王在高.大圆航程与恒向线航程的比较分析[J].合肥学院学报,2016,33(4):13-17.
WANG Zai-gao.Comparative Analysis of Distance Between Great Circle and Rhumb Line[J].Journal of Hefei University,2016,33(4):13-17.
[8] 孙继红,赵杨,杜晓海.反潜自导鱼雷不同航速下的航程计算[J].舰船电子工程,2012,32(8):39-41.
SUN Ji-hong,ZHAO Yang,DU Xiao-hai.Range Calculating in Different Speed Conditions for Anti-Sumarine Homing[J].Ship Electronic Engineering,2012,32(8):39-41.
[9] 孙权.能量约束下鱼雷最优攻击速度和提前角[J].鱼雷技术,2017,25(1):77-81.
SUN Quan.Optimal Attack Speed and Leading Angle of Torpedo Under Energy Constraint [J].Torpedo Technology,2017,25(1):77-81.
[10] 张耀中,李寄伟,胡波.基于改进ACO算法的多UAV协同航路规划[J].火力与指挥控制,2017,42(5):139-146.
ZHANG Yao-Zhong,LI Ji-wei,HU Bo.Cooperative Path Planning for Multi-UAVs Based on Improved ACO Algorithm[J].Fire Control & Command Control,2017,42(5):139-146.
[11] 刘长龙,王勇,任杨,等.基于航程补偿的高超声速飞行器轨迹快速规划[J].计算机仿真,2015,32(10):78-82.
LIU Chang-long,WANG Yong,REN Yang,et al.Rapid Trajectory for Hypersonic Vehicle Based on Flight Range Compensation[J].Journal of Computer Simulation,2015,32(10):78-82.
[12] 许泽宇,王洪波,康永来.返回式滑翔飞行器最小航程轨迹优化方法[J].导弹与航天运载,2017,352(2):25-30.
XU Ze-yu,WANG Hong-bo,KANG Yong-lai.Trajectory Optimization Research for Reentry Glide Vehicle With Minimum-Range Constraint[J].Missiles and Space Vehicles,2017,352(2):25-30.
[13] 沈立项,王和平,练彬.轻型电动载人飞行器航程与航时计算方法研究[J].西北工业大学学报,2015,33(4):553-558.
SHEN Li-xiang,WANG He-bing,LIAN Bin.Range and Endurance Estimates for Light Electric Manned Aircraft[J].Journal of Northwestern Polytechnic University,2015,33(4):553-558.
[14] 从书全,王成军,姜杨.无人机航程与续航时间的实时估算方法研究[J].宇航计测技术,2012,32(2):62-65.
CONG Shu-quan,WANG Cheng-jun,JIANG Yang.Research on Real-Time Estimation Method for Range and Cruise Duration of UAV[J].Journal of Astronautic Metrology and Measurement,2012,32(2):62-65.
[15] YANG Hua-dong,REN Xiao-jun.An Improved Algorithm for the Solution of Geodetic Problems[C]∥2009 International Joint Conference.Proceedings of the Second International Joint Conference on Computational Sciences and Optimization.US:IEEE,2009:218-220.
