Adjexpectile风险测度的性质、优化及资产配置的应用

周 静, 罗 乐

(华中科技大学管理学院，湖北 武汉 430074)

1 引言

在金融风险管理中找到一个合适的风险度量是非常具有挑战性的，不同的风险度量对资产定价、组合对冲、资产配置、投资绩效评价产生不同的影响。当我们主要关注下侧风险时，对收益的上升和下跌变化的管理是不同的[1-2]。VaR是主要的下侧风险度量工具。VaR定义为在给定置信水平下，一个组合在一段时间内最大的损失。概念上VaR把组合的市场风险归结为一定量的货币(或百分比)，由于概念的简单，受到金融实务者、监管者和政策制定者的广泛接受。VaR可以表示为标的资产收益分布第α分位数的绝对值，给定尾部概率α，α分位数仅仅依赖于极端事件的分布，而不是极端事件的损失,对极端事件损失是不敏感的。Kuan等[3]构建了两个具有相同的分位数而不同尾部行为的例子说明这种情况。另外，VaR不是次可加性风险度量，Artzner等[4]、Acerbi等[5]认为一个组合的总风险不应该大于各成分资产风险之和。由于VaR作为风险度量工具的不足，Artzner等[4]、Yamai和Yoshiba[6]提出期望损失(ES)作为风险度量工具克服VaR的不足，并得到广泛的应用。ES定义为收益超过VaR条件下收益的期望值。

VaR其实就是Koenker等[7]提出的分位数回归(QR)的特例，相对于传统的均值回归QR可以研究不同位置的条件分布，全局性的考察了因变量和自变量的相互关系，它的吸引力不仅体现在数据的异方差性，而且还可处理不同误差分布特征的数据，在经济、金融领域得到广泛的应用。但由于非对称加权绝对误差函数不连续可微，及估计量的协方差矩阵依赖于误差密度函数在对应分位数的值，给估计和检验带来困难。为了弥补这个缺陷，Aigner等[8]提出了类似分位数回归的最小平方法，Newey和Powell[9]把该方法定义为“非对称最小二乘”估计(ALS)，并进行拓展，提出expectile的概念，并证明了expectileμ(τ)关于τ(τ∈(0,1))是严格单调增加的，正齐次性和平移不变性，类似于分位数的性质。如果把|μ(τ)|作为保证金需求[3,10]，τ可以表示为期望边际损失的相对成本，当保证金需求越多，边际损失就越小，τ就越小，违约风险越小，所以把τ视为防止违约风险的谨慎性水平。根据Yao等[11]和Efron[12]的思想，可以建立expectile和ES(α)的线性关系，expectile具备ES(α)所具有的超可加性，弥补了VaR的不足。另外，我们利用混合正态分布揭示了expectile对极端风险的敏感性，这种敏感性不同于ES，类似于Kuan等[3]利用模特卡罗实验的结果。

鉴于expectile 的严格单调增加性、正齐次性、平移不变性、超可加性、谨慎性和对极端事件的敏感性等优良性质，作为金融风险度量工具具有优越性。在资本加速全球化时代，大量的资本在全球范围内自由流通和运转，使的金融体系稳定性下降，金融市场波动显著增加，市场风险加剧。导致金融风险愈加复杂和多样化，极端灾难性金融事件频繁发生。一个合适的金融风险度量显得尤其重要，对资产配置和动态调整策略具重要的经济意义和实践价值。我们的目标就是提出一个替代性的资产配置的方法，通过定义、度量、分析和优化，表示和均值方差、均值shortfall不同的概念，并表明它的可计算性具有很好的实际应用。

经典的组合配置方法是马科维茨的均值方差模型，用标准差作为风险度量，优化收益和风险的权衡。组合的方差涉及到组合所有成分的协方差，增加了经济含义，得到广泛的实际应用，但模型的二次效用和椭圆对称收益分布受到批判[13-14]。由于标准差度量风险存在以上问题，产生一系列对标准差替代性风险度量。Fishburn[2]提出均值风险方法，记为(α,t)模型。Manganelli[15]通过惩罚最小二乘法(PLS)解决对应的(α,t)模型组合资产配置问题。Dowd[16]、Duffie等[17]使用分位数作为下侧风险度量工具，但极端事件发生的概率是无法预期的，VaR不能度量这些期望损失，Basak等[18]也表达同样的观点。为了解决这个问题，Artzner等[4]给出了风险度量的一致性公里，证明了VaR不满足次可加性，损坏了风险的分散，并给出尾部条件期望(TailVaR、TCE、ES、CVaR)，证明满足一致性公里。Uryasev 和 Rockafellar[19]提出一种新的方法求解最小CVaR资产配置和组合对冲策略，该方法的优越之处是把最小化ES转化为线性规划问题，不依赖于收益的概率分布，还可以顺便求解出VaR。Bertsimas等[20]从二阶随机占优的角度引进shortfall作为风险度量工具，分析了它的风险度量一致性、凸性等性质，讨论了与标准差、VaR、LPM之间的关系，并通过非参数的方法转化为线性规划求解均值shortfall的组合优化及有效前沿。

本文主要贡献体现在以下四个方面：第一、在混合正态分布下揭示expectile的风险敏感性, 类似于Kuan等[3]利用模特卡罗实验的结果；第二、定义了Adjexpectile风险度量，并讨论和分析了Adjexpectile的一致性风险度量、随机占优性、凸性,与标准差、VaR、shortfall的关系，风险贡献及风险分解；第三、讨论了Adjexpectile的估计方法；第四、利用六个指数的周收益数据对均值标准差、均值shortfall、均值Adjexpectile的有效前沿比较，并对组合权重的差异和风险进行分析。

2 Expectile的风险敏感性

VaR可以表示为标的资产收益分布第α分位数的绝对值，第α分位数可以通过最小化以下非对称加权绝对误差函数获得：

Ε[|α-1{Y≤q}|·|Y-q|]

(1)

通过(1)式的最小化一阶条件，得到：

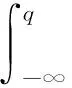
(2)

(1)式可以看作通过非对称权重描述悲观情绪[21]。

ES定义为收益超过VaR条件下收益的期望值。如(3)式所示：

ES(α)=Ε[Y|Y≤-VaRα]

(3)

Newey和Powell[9]用非对称最小二乘定义的expectile,如(4)式所示：

(4)

其中τ∈(0,1)。μ(τ)被认为Y的第τexpectile，τ=0.5，(4)式就是传统的最小二乘函数，μ(0.5)就是均值Ε[Y]。

从(4)式可以得到：

μ(τ)=γΕ[Y|Y>μ(τ)]+(1-γ)Ε[Y|Y≤μ(τ)]

(5)

其中，

γ=τ[1-FY(μ(τ))]/{τ[1-FY(μ(τ))]+(1-τ)FY(μ(τ))}。

Expectile 可以看做上侧条件均值和下侧条件均值的加权平均。另外，(4)式也可变化为相对数的形式τ=Ε[|Y-μ|1{Y≤μ}]/Ε[|Y-μ|]，Kuan等[3]及Lam等[10]把|μ(τ)|作为保证金需求，Ε[|Y-μ|1{Y≤μ}]代表期望边际损失，Ε[|Y-μ|1{Y>μ}]代表期望边际机会成本，Ε[|Y-μ|]就是二者的总成本。当|μ(τ)|越大时，期望边际损失越小，τ就越小，但机会成本提高，金融市场中交易清算机构就把τ作为谨慎性指数，防止违约风险。Yao等[11]建立了τ和α如(6)式所示关系式，Efron[12]提出α分位数可以通过expectile来估计的思想：样本内观测值低于expectile的比例是α，使得μ(τ)=q(α)。

(6)

其中α∈(0,1)。由(5)式可以得到用ES(α)表示的μ(τ)：

(7)

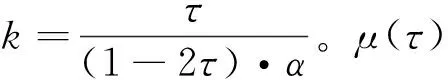
从图1中可以看到expectile 的斜率在τ=0.5附近小于对应的分位数的斜率，和ES的斜率几乎相同，在靠近τ=0时expectile 的斜率要大于对应的分位数和ES的斜率，说明expectile在左尾部是非常敏感的。τ=0.5时，对应分位数为中位数，expectile为均值，对于一般的非对称分布，二者可能不相等。

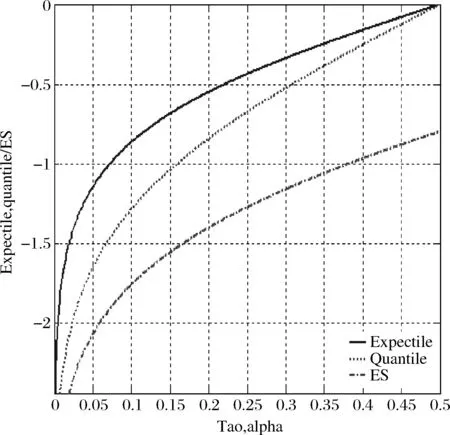
图1 μ(τ)τ∈(0,0.5)在标准正态分布下的图形

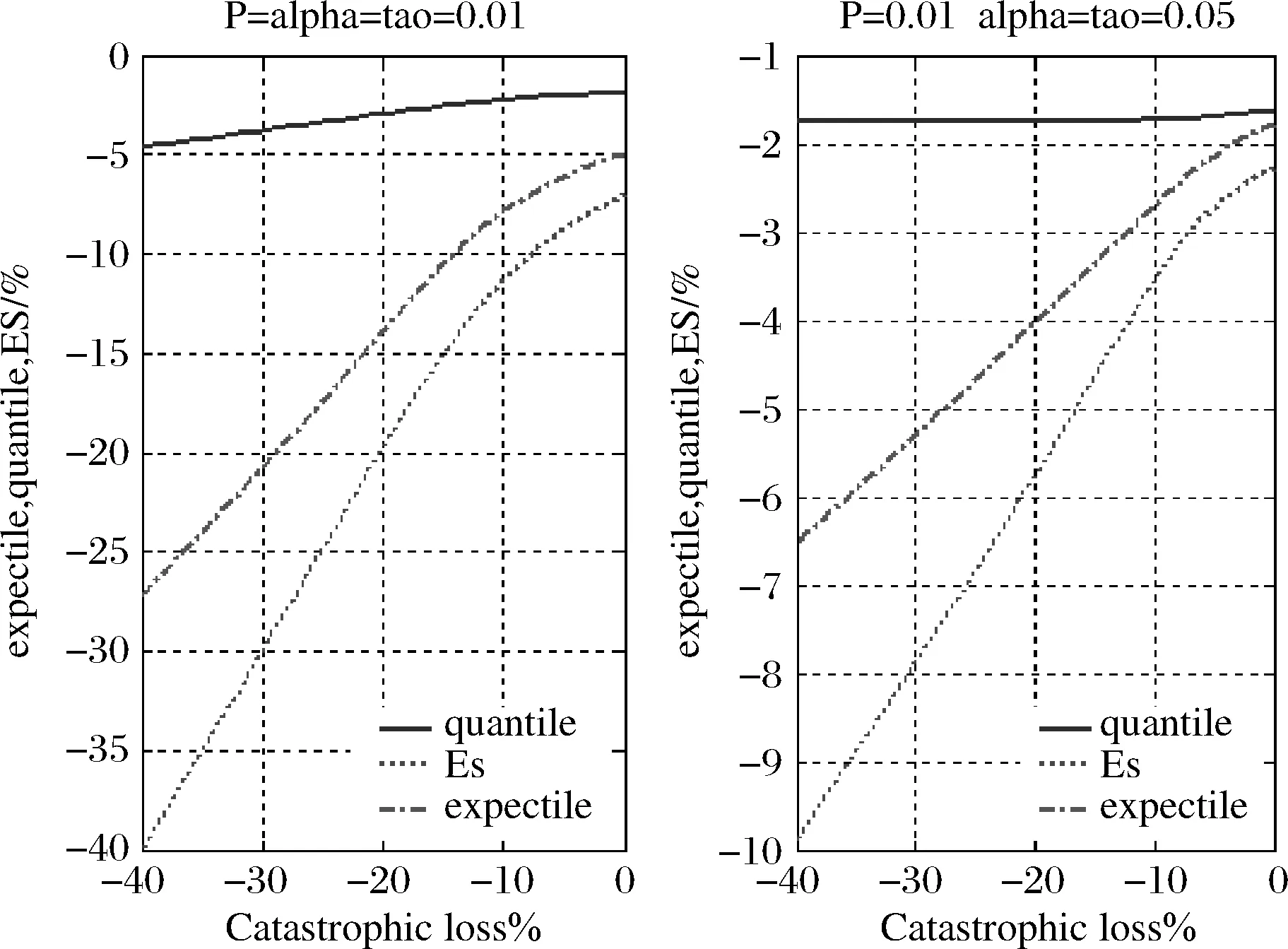
图2 Quantile、Expectile、ES对极端损失的敏感性

在图1中，当μ(τ)=q(α)=ES(α)时，τ<α，τ作为谨慎性指数反映了风险暴露水平要小。由(6)式可以计算出，在标准正态分布下，τ=1%、2%、5%、10%、25%、50%，α=4.29%、6.97%、12.71%、19.45%、33.13%、50%；在厚尾分布t(6)下，α=2.97%、5.21%、10.46%、13.93%、31.5%、50%。相同的τ值，α值的大小依赖于尾部分布，反映了不同概率水平下的风险暴露。

3 Adjexpectile的定义和性质

3.1 Adjexpectile的定义

这部分，利用期望效用范式和随机占优定理来定义Adjexpectile。在投资者设定的效用函数u(·)下，投资者按照期望效用最大化进行选择，也就是说Ε(u(X))≥E(u(Y))，投资者偏好投资收益X。一般情况下，效用函数集合U可分为两类：单调不减函数类U1，可理解为“收益越多越好”，称为一阶随机占优；单调不减凹函数类U2，是“风险厌恶”的，称为二阶随机占优。因为套利机会的存在，一阶随机占优很难发生，一阶随机占优是二阶随机占优的必要非充分条件。另外，理论上可能存在更高阶的占优，但实践中高于二阶的随机占优是不明显的。马科维茨均值方差准则如果通过效用函数或随机变量来定义，只能用二次效用或椭圆对称收益分布来定义，其优缺点在引言部分已叙述。

下面考虑n个资产的组合，假设随机收益向量R=(R1,…,Rn)′联合密度函数是连续的，均值μ=Ε[R]，权重为x=(x1,…,xn)′的组合收益X=R′x。对于给定的组合均值Ε[R′x]=μ′x，投资者最大他们的期望效用Ε[u(X)]。

在效用函数Ui,i=1,2下，用Levy定理[22]来刻画投资者偏好：

定理1(Levy 1992)：随机变量X、Y有连续密度函数：

(a)Ε[u(X)]≥Ε[u(Y)],∀u∈U1,当且仅当qα(X)≥qα(Y),∀α∈(0,1)。

(b)Ε[u(X)]≥Ε[u(Y)],∀u∈U2，当且仅当Ε[X|X≤qα(X)]≥Ε[Y|Y≤qα(Y)],∀α∈(0,1)。

根据定理1, 当投资者的效用函数u∈U1时，最大化投资者期望效用Ε[u(X)]，相当于对qα(R′x)求最大值，对VaRα(x)=μ′x-qα(R′x)求最小值，由于非凸性和非次可加性，给计算和风险分散带来难度。VaRα(x)给出了低于期望收益损失的大小，发生的概率不大于α。当投资者的效用函数u∈U2时，最大化投资者期望效用Ε[u(X)]，相当于对ESα(R′x)求最大值，对Sα(x)=μ′x-ESα(R′x)求最小值，Sα(x)表示当组合收益不大于它的α分位数时，平均收益低于期望收益损失的大小，Bertsimas等[20]把它命名为shortfall。

Expectileμ(τ)对∀τ∈(0,0.5)由(7)式所示，(7)式等价为：

(8)

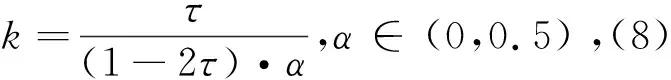
(9)

当投资者的效用函数u∈U2时，最大化投资者期望效用Ε[u(X)]，由(7)式相当于对μτ(R′x)求最大值，对Sτ(x)=μ′x-μτ(R′x)求最小值。本文把Sτ(x)叫做均值调整的expectile，简记为Adjexpectile。表示当组合收益低于它的τ分位数的条件下对下侧均值惩罚权衡后，低于期望收益损失的大小。Sτ(x)是组合权重的函数，也是组合收益X的函数，在本文中二者是相等的Sτ(x)=Sτ(X)。

3.2 Adjexpectile的性质

为了加深对Adjexpectile的理解，这部分我们讨论了它的一致性风险度量，凸性、风险度量相关性、边际贡献。

定义1：一致性风险度量

Artzner等[4]认为每个风险度量应该满足四个公理，Delbaen[23]把这四个公理由离散概率空间扩展到任意概率空间。随机收益X的一致性风险度量ρ(X)是一个实值函数，满足：

(1)平移不变性：对任意的实数a，ρ(X+a)=ρ(X)+a

(2)次可加性：对任意的随机变量X、Y，ρ(X+Y)≤ρ(X)+ρ(Y)

(3)正齐次性：当t≥0,ρ(tX)=tρ(X)

(4)单调性：如果X≥0，ρ(X)≤0

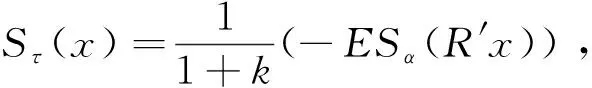
下面我们来证明Sτ(x)满足次可加性和正齐次性。

命题1：对任意的随机变量X、Y，Sτ(X+Y)≤Sτ(X)+Sτ(Y)

证明：让X、Y表示n个资产的组合收益，权重分别为x=(x1,…,xn)′，y=(y1,…,yn)′，X=R′x,Y=R′y。ESα(X)定义如(2)式所示。ESα(X)可以等价的表示为：

(10)

连续分布函数F(a)=α.

E(X)=αE[X|X≤qα(X)]+(1-α)E[X|X>qα(X)]=αESα(X)-(1-α)ES1-α(-X)

E(X)-ESα(X)=-(1-α)[ESα(X)+ES1-α(-X)]

(11)

(12)

用-(X+Y)替换(12)式X+Y，ES1-α(-X)同样满足(12)式的不等式。由(9)式、(11)式、(12)式得到：

(13)

命题2：当t≥0,Sτ(tX)=tSτ(X)

证明：对任意的t≥0，qα(tX)=tqα(X)是显然的，

命题3：Adjexpectile是凸函数，对任意的0<γ<1，Sτ(λX+(1-λ)Y)≤λSτ(X)+(1-λ)Sτ(Y)。

由命题1和命题2很容易得到命题3。

命题4：Adjexpectile与shortfall、VaR、标准差之间的关系

(1)由Adjexpectile定义

(2)当μ(τ)=q(α)时，Sτ(x)=VaRα(x)。

(3)如果n个资产收益向量R服从椭圆对称分布，均值μ，协方差为Σ，

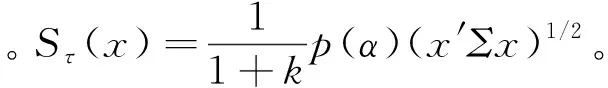
命题4(1)和(2)由Adjexpectile定义得到，(3)的证明参考Bertsimas等[20]命题1。

命题5：Adjexpectile的风险贡献及欧拉分解：

(14)

(15)

(14)式的证明参考Bertsimas等[20]命题3。由于Sτ(x)的正齐次性及欧拉定理(15)式得证。

4 Adjexpectile组合的优化

这部分我们考虑Adjexpectile的组合优化问题。

(16)

e是单位列向量，(16)式定义类似于均值shortfall[20]组合优化问题：

(17)

均值方差组合优化问题：

(18)

(18)式可以采用二次规划进行优化，对于(17)式优化问题，Bertsimas等[20]采用非参数方法样本化均值shortfall优化问题，最后归结为较少数目的约束(二倍样本规模加二加组合资产数)和变量(组合资产数加一加样本规模)的线性规划。该方法的优势不需要对收益R的分布做任何假设，直接利用历史数据。

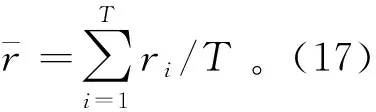
(19)

对(17)式采用类似Uryasev等[19]线性规划法，我们也可得到(19)式，但样本r1,…,rT不是历史数据，而是历史收益联合概率分布产生的随机样本，需要假设一个概率分布。这里需要说明的是历史收益率的时间序列含有市场可行的信息，决定市场的不变性，特别是时间齐次不变性收益率的时间序列，它的分布不依赖于时间点，很容易得到任何时间区间的分布。权益市场主要使用复合收益率表示时间齐次不变性。市场不变性收益分布的估计可采用非参数法和参数方法，对于大样本采用非参数法方法比较好，Bertsimas等[20]用的就是这个思想。不是大样本情况下一般采用参数估计，比如极大似然估计、收缩估计(Shrinkage)等，Uryasev等[19]用的是后者方法。除此之外还有稳健性估计，比如稳健性M估计。本文采用Bertsimas等[20]方法得到(16)式的线性规划问题。

定理2:问题(16)等价于线性优化问题：

(20)

证明参考Bertsimas等[20]定理3。

5 均值Adjexpectile组合配置实证分析

这部分为了解释风险度量Adjexpectile的组合优化和风险分析，使用了3个资产分类债券、权益和黄金现货，六个指数：上证国债指数、上证企业债指数、上证180指数、深圳100指数、深成长40p指数和黄金现货Au9999指数。为了结果的稳健性，我们也给出了风险度量shortfall和标准差的组合优化。

5.1 数据和描述统计量

六个指数的时间范围从2006年6月到2016年6月共489周，所有的收益率采用周复合收益率，指数数据来源于国泰安CSMAR数据库。

表1反映了每项资产买进并持有策略统计量，我们看到平均周收益率最高的是深圳成长40p指数达到0.24%，其次是深圳100指数达到0.20%，有趣的是深圳100指数周平均波动率要比深圳成长40p指数高0.04个百分点，最大下跌量小1.60个百分点。周平均收益率、波动率最小的是上证国债指数，分别为0.06%、0.07%，上证企业债几乎是它们的二倍，二者的偏度大于零，说明是右偏态的，二者峰度都较大，呈现尖峰状，但上证企业债的峰值更大。其余四个指数是左偏态的，峰值在2左右。两个债券指数拥有最有吸引力的夏普比率分别为0.4118和0.3236,让人感到意外的是上证180指数及黄金现货的夏普比率最低。

另外，也检验了六个指数的皮尔逊相关性，从未列表数据观察到，三个权益指数有高度的正相关性，最高达到0.95，但与两个债券指数存在显著负相关的，负相关程度国债稍微高于企业债，这也意味着国债指数在股票市场熊市期间可以作为一个很好的风险分散工具。两个债券指数存在显著的正相关，相关系数为0.58。而黄金现货指数收益率与其它五个指数收益率几乎是不相关的。

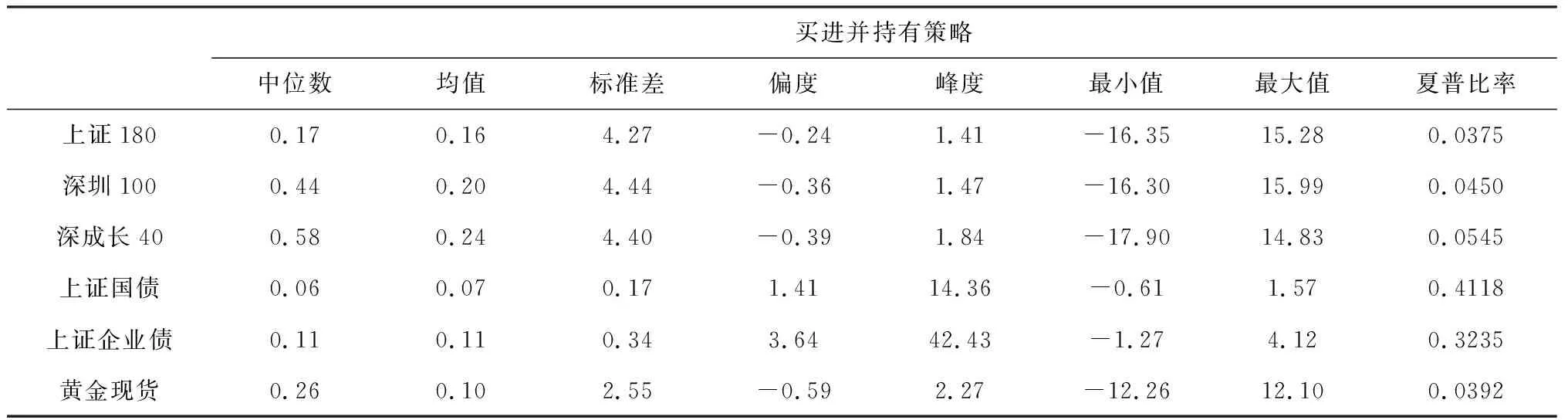
表1 资产收益的描述统计量

5.2 给定的τ 值，α 值的估计

根据(8)式，Adjexpectile的计算需要在给定τ值的情况下，获得对应的α值。根据Efron[12]用expectile估计分位数的思想，样本内观测值低于τexpectile的比例是α，也就是说对于每个τexpectile对应着一个α分位数，虽然τ不等于α，但存在expectile与分位数的一对一对应关系。Enger等[24]用半参数方法基于CAViaR模型进行分位数回归，避免了分布假设。Taylor[25]把CAViaR模型拓展到CARE模型用于非对称最小二乘(ALS)回归，回归的结果就是expectile，目的是用expectile估计ES。这部分我们采用类似Taylor[25]的CARE模型求出τexpectile，然后根据Efron[12]的思想，求出对应分位数的α。

具体估计过程为：首先，对模型(21)和(23)式，用(0,1)均匀分布产生104个3维随机向量，使(4)式最小的10个向量作为模型参数估计的初始值。而对模型(22)和(24)式，用(0,1)均匀分布产生105个4维随机向量，使(4)式最小的15个向量作为模型参数估计的初始值。其次，对于每个模型，在给定τ值和5.1节提到的489周给定指数的时间收益序列，用Matlab程序的无约束线性优化函数fminsearch 求出使(4)式最小的参数。最后，对每个模型和每个指数，求出τexpectile，并计算所有样本中小于τexpectile的样本占总样本的比例，就是我们要估计的α。Taylor[25]的CARE模型表示如下：

对称绝对值CARE模型(SAV):

μt(τ)=β0+β1μt-1(τ)+β2|rt-1|

(21)

非对称斜率CARE模型(AS):

μt(τ)=β0+β1μt-1(τ)+β2(rt-1)++β3(rt-1)-

(22)

间接GARCH(1,1)CARE模型:

μt(τ)=(1-2I(τ<0.5))(β0+β1μt-1(τ)2+

(23)

间接AR(1)- GARCH(1,1)CARE模型:

μt(τ)=α1rt-1+(1-2I(τ<0.5))(β0+

β1(μt-1(τ)-α1rt-2)2+β2(rt-1-α1rt-2)2)1/2；βi>0

(24)

SAV模型和GARCH模型表明过去的收益对现在expectile的影响是对称的，AS模型表明过去正、负收益的对现在expectile的影响是不同的，具有杠杆效应。Enger等[24]用前三个CAViaR模型来解释基于现在信息组合收益的未来VaR的值，并给出动态分位数检验(DQ)。间接AR(1)- GARCH(1,1)CARE模型是由Kuester等[26]提出的，目的通过α1来抓住收益序列的自相关关系。这四个模型通过expectile的滞后项实现均值回复。模型的参数采用非对称最小二乘函数(4)式来估计。苏幸等[27]用CARE模型对基金业绩进行评价，谢尚宇等[28]用ARCH-Expectile对VaR和ES进行风险度量。本文在上述四个模型基础上，按照Efron[12]对α的解释，及对应的估计程序，得到表2的结果。

在表2中，对于给定的τ及不同的指数，GARCH和ARGARCH模型估计的α值几乎惊人的相等，和AS模型估计的α值比较接近，但与SAV模型估计的α值在上证180指数和上证企业债指数上差别还是很大的。Enger等[24]对CAViaR模型的设定认为更一般化，可以用于各种形式具有非独立同分布误差项的收益时间序列。简志宏等[29]用CAViaR模型对沪深300股指期货隔夜风险进行研究，发现对于左尾部，AS模型要比SAV和间接GARCH模型优越。Taylor[25]用上面的四个CARE模型求expectile时，发现GARCH模型和SAV模型要优于AS模型。由于本文用的六个指数数据特征比较复杂，有左偏态的，也有右偏态和尖峰的，所以没有对不同的CARE模型对不同数据的优越性进行比较。为了消除不同的模型估计α值的偏差，我们取四个CARE模型对不同指数估计的α值的平均值。τ=1%、5%时，α=3.0998%、10.0971%，这个结果说明τ值比对应的α值更极端，这个与第2部分在标准正态分布下的图1结论一致，另外也与t(6)分布下α=2.97%、10.46%的估计结果很接近。

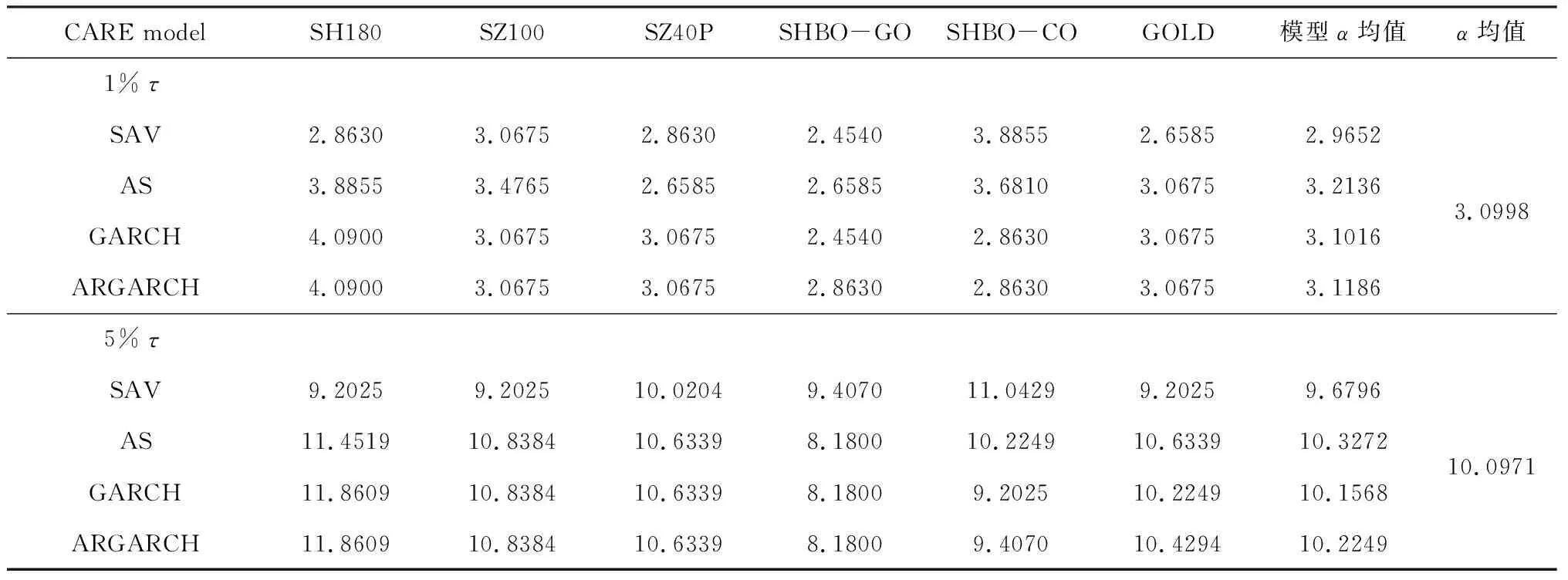
表2 给定的τ 值，在CARE模型下得到α 值

5.3 均值Adjexpectile组合的有效前沿

这部分我们利用489周的历史周收益数据对(20)式进行优化，此时取τ=1%，α=3.1%。对于均值shortfall(19)式的优化，取α=1%。对于均值标准差的优化，采用传统的二次规划。我们规定是全投资且不允许做空(天下没有免费的午餐)，优化约束要求权重之和等于1且各组合权重是非负的。图3左图反应了收益标准差的权衡，右图反应了收益99%shortfall的权衡。从左图中可以看到以标准差作为风险度量，99%Adjexpectile组合前沿要优于99%shortfall组合前沿，和均值标准差组合前沿重合。右图在99%shortfall作为风险度量下，99%Adjexpectile组合前沿要优于99%shortfall组合前沿，这个和我们第2部分敏感性分析是吻合的。在第1部分文献回顾部分，我们认为标准差对上侧和下侧收益风险是一样看待的，expectile、shortfall作为下侧风险度量工具，图3的结果正体现了expectile作为风险度量的魅力。

最优权重及风险贡献作为收益目标的函数报告在图4中，第一行、第二行、第三行分别为Mean-StdDev、Mean-Shortfall、Mean-Adjexpectile有效前沿组合权重和风险贡献。从第一列有效前沿组合权重上发现当目标收益小于0.1%时，权重主要配置国债和企业债，随着目标收益增加，国债的权重在减少和企业债的权重在增加。当目标收益大于0.1%时，随着目标收益增加，国债的权重减少为零，企业债的权重也在减少，深圳成长40p指数的权重在增加。造成这个现象并不感到惊讶，这个结果和表1中反应的数据统计特征相吻合的。表1中最大夏普比率依次为上证国债指数、上证企业债指数和深圳成长40p指数，且债券指数和股票指数是负相关的，黄金现货指数和它们几乎是不相关的，所以在有效组合权重配置中完全反映了这些数据特征。从第二列有效前沿组合风险贡献上发现较大的区别，均值Adjexpectile资产配置要比均值Shortfall、均值标准差资产配资更加分散，这进一步体现它的优势。当目标收益大于0.15%时，发现组合几乎所有的风险来自深圳成长40p指数，Litterman[30]把这样的头寸称为‘Hot Spots’，识别了最优组合的‘Hot Spots’，也就识别了潜在风险对冲对象，有助于组合的风险管理。

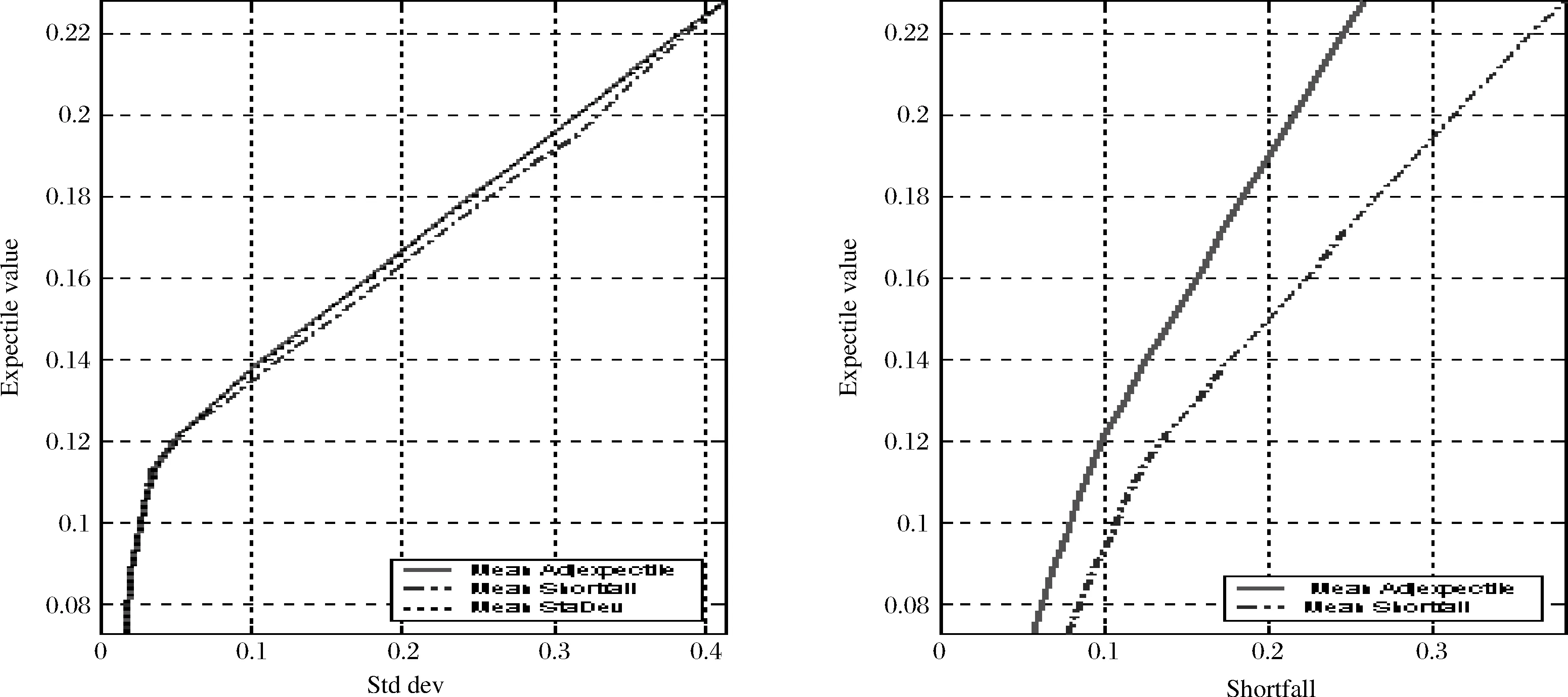
图3 Mean-StdDev、Mean-Shortfall、Mean-Adjexpectile有效组合前沿，τ=1%，α=1%

6 结语

作为下侧风险度量工具expectile与传统的VaR、ES比较，得出expectile 的严格单调增加性、正齐次性、平移不变性、超可加性、谨慎性和对极端事件的敏感性等优良性质，表现出作为金融风险度量工具的优越性。在此基础上本为提出Adjexpectile的概念，经济、金融含义可以理解为：在组合收益低于它的τ分位数条件下对下侧均值惩罚权衡后，低于期望收益损失的大小。并进一步讨论了Adjexpectile的二阶占优性、正齐次性、次可加性、凸性及与标准差、VaR、shortfall的关系，风险贡献及风险分解。借助shortfall组合优化方法，我们得到Adjexpectile的线性规划组合优化方法。在实证部分，我们使用中国资本市场上具有代表性的六个资产指数：上证国债指数、上证企业债指数、上证180指数、深圳100指数、深成长40p指数和黄金现货指数，作为我们组合研究对象。对置信水平τ的Adjexpectile，我们采用对称绝对值CARE模型、非对称斜率CARE模型、间接GARCH(1,1)CARE模型、间接AR(1)- GARCH(1,1)CARE模型分别计算出对应分位数的α水平，取平均的α值参与组合优化,与标准差、shortfall相比，发现Adjexpectile在非对称性收益数据、组合前沿、风险分散方面具有一定的优越性。

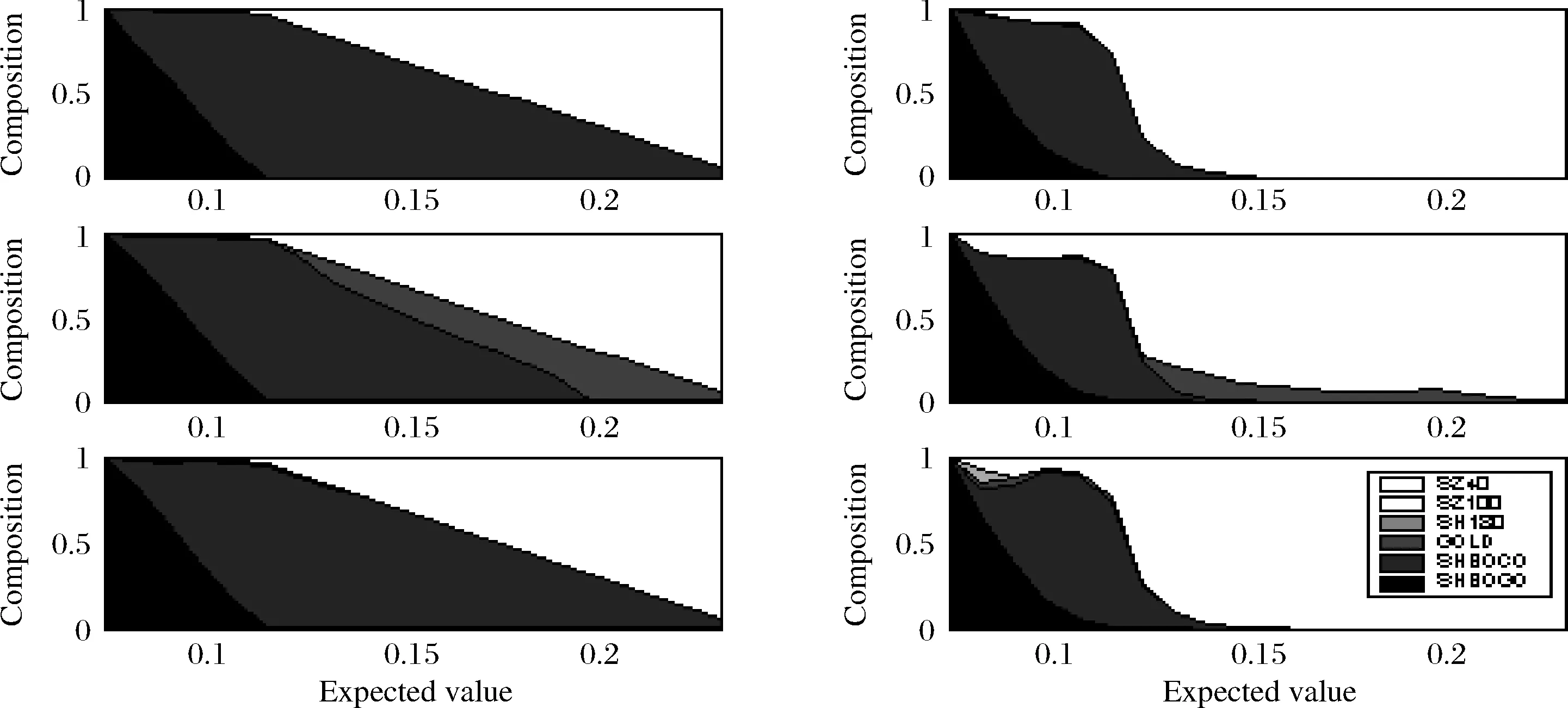
图4 Mean-StdDev、Mean-Shortfall、Mean-Adjexpectile有效组合权重和风险贡献τ=1%，α=1%

参考文献：

[1] Markowitz H. Portfolio election[J]. Journal of Finance, 1952,7(1):77-91.

[2] Fishburn P. Mean risk analysis with risk associated with below target returns[J]. American Economic Review,1977,67(2):116-126.

[3] Kuan C, Yeh J, Hsu Y. Assessing value at risk with CATE,the conditional autoregressive expectile models[J]. Journal of Econometrics, 2009,150(2):261-270.

[4] Artzner P, Delbain F, Eber J M, et al. Coherent measures of risk[J]. Mathematical Finance, 1999,9(3):203-228.

[5] Acerbi C, Tasche D. On the coherence of expected shortfall[J]. Journal of Banking and Finance, 2002,26(7):1487-1503.

[6] Yamai Y, Yoshiba T. On the validity of Value-at-Risk: Comparative analyses with expected shortfall[J].Monetary and Economic Studies, 2002,20(1):57-85.

[7] Koenker R, Bassett G S. Regression quantiles[J]. Econometrica,1978,46(1):33-50.

[8] Aigner D J, Amemiya T, Poirier D J. On the estimation of production frontiers:Maximum likelihood estimation of the parameters of a discontinuous density function[J]. International Economic Review, 1976,17(2):377-396.

[9] Newey W K, Powell J L. Asymmetric least squares estimation and testing[J].Econometrica, 1987,55(4):819-847.

[10] Lam K, Sin C Y, Leung R. A theoretical framework to evaluate different marginsetting methodologies[J]. Journal of Futures Markets,2004,24(2):117-145.

[11] Yao Q, Tong H. Asymmetric least squares regression estimation: A nonparametric approach[J]. Nonparametric Statistics, 1996,6(2):273-292.

[12] Efron B. Regression percentiles using asymmetric squared error loss[J]. Statistica Sinica, 1991,1(1):93-125.

[13] Huang C F, Litzenberger R H. Foundations for financial economics[M]. New Jersey: Prentice Hall, 1988.

[14] Hamao Y, Musulis R, Ng V. Correlations in price changes and volatility across international stockmarkets[J]. The Review of Financial Studies,1990,3(3):281-307.

[15] Manganelli S. Asset allocation by penalized least squares[R]. Working Paper, European Central Bank, 2007.

[16] Dowd K. Beyond value at risk:The new science of risk management[M]. New York: Wiley, 1999.

[17] Duffie D, Pan Jun. An overview of value at risk[J]. Journal of Derivatives, 1997,4(3):7-49.

[18] Basak S, Shapiro A. Value-at-Risk based risk management:Optimal policies and asset prices[J]. The Review of Financial Studies, 2001,14(2):371-405.

[19] Uryasev S, Rockafellar R T. Optimization of conditional Value-at-Risk[J].Journal of Risk,1999,29(1):1071-1074.

[20] Bertsimas D, Lauprete G, Samarov A. Shortfall as a risk measure:Propertyes,optimization and applications[J]. Journal of Economic Dynamics & Control, 2004,28(7):1353-1381.

[21] Bassett G W, Koenker R, Kordas G. Pessimistic portfolio allocation and Choquet expected utility[J]. Journal of Financial Econometrics, 2004,2(4):477-491.

[22] Levy H. Stochastic dominance and expected utility: Survey and analysis[J].Management Science,1992,38(4):555-593.

[23] Delbaen F. Coherent risk measures on general probability spaces[M].Berlin Heidelberg:Springer,2002.

[24] Engle R F, Manganelli S. CAViaR: Conditional autoregressive Value-at-Riskby regression quantiles[J].Journal of Business & Economic Statistics, 2004,22(4):367-381.

[25] Taylor J W. Estimating Value-at-Risk and expected shortfall using expectiles[J]. Journal of Financial Econometrics, 2008,6(2):231-252.

[26] Kuester K, Mittnik S, Paolella M S. Value-at-Risk prediction: A comparison of alternative strategies[J]. Journal of Financial Econometrics, 2006,4(1):53-89.

[27] 苏幸, 周勇. 条件自回归expectile模型及其在基金业绩评价中的应用[J].中国管理科学，2013,21(6):22-19.

[28] 谢尚宇, 姚宏伟, 周勇. 基于ARCH-Exp-ectile方法的VaR和ES尾部风险测量[J].中国管理科学, 2014,22(9):1-9.

[29] 简志宏, 曾裕峰, 刘曦腾. 基于CAViaR模型的沪深300指数期货隔夜风险研究[J]. 中国管理科学, 2016,24(9):1-10.

[30] Litterman R. Hot spotsTMand hedges[J].Journal of Portfolio Management,1996,Special Issue:52-75.