基于磁激元效应的石墨烯-金属纳米结构近红外吸收研究∗
2018-06-19陈浩张晓霞王鸿姬月华
陈浩 张晓霞 王鸿 姬月华
1 引 言
石墨烯作为一种蜂窝状有序排列的单碳原子层结构[1],具有独特的零带隙电子能带结构,在狄拉克点附近具有线性能量散射的特性,与传统半导体相比在力学、光学和电学特性方面具有不可比拟的优势[2,3].石墨烯具有很高的载流子迁移率[4],这使得石墨烯成为构建超快光学器件的潜在材料[5,6].然而石墨烯作为单碳原子层结构,厚度仅为0.34 nm,这导致石墨烯在近红外和可见光波段与电磁波的相互作用相对较弱,其吸收率只能达到2.3%[7].这一特性有利于石墨烯在显示[8]、发光二极管[9]等领域的应用,但是在诸如光电探测、光电调制、太阳能电池等对材料吸收率及吸收可调性有更高要求的领域,石墨烯对光吸收能力的不足限制了它的应用.如何提高石墨烯在近红外和可见光波段对光的吸收,并且实现吸收动态可调已经吸引了诸多研究者的关注.
石墨烯在电磁波的不同波段显示出了不同的吸收特性.在中红外到太赫兹波段,石墨烯类似于Drude类型[10]材料展示出了较强的等离激元响应[11],因此将石墨烯结构化为带状[12−14]、盘状[15]等可以激发石墨烯的表面等离激元(surface plasmon polaritons,SPPs)[16],进而获得较好的吸收增强.然而在可见光和近红外波段,石墨烯表面无法激发出SPPs响应.为了克服石墨烯在可见光和近红外波段应用的限制,Marco等[17]和Liang等[18]提出将石墨烯放置于微腔之中,利用微腔中入射光往复穿透石墨烯层,实现石墨烯在近红外波段的吸收增强.不过,微腔结构尺寸较大,不利于石墨烯在光电领域应用的集成化.将石墨烯与能产生表面等离激元的微纳结构[19−21]相结合,利用微纳结构奇特的局部光场增强特性,可以实现亚微米尺寸下的石墨烯吸收增强.Fang等[22]提出将高分子聚合物的纳米颗粒耦合到石墨烯的表面,在入射光下通过SPPs效应增强局域光场.Cai等[23,24]利用超材料完美吸收体中的超薄夹缝波导模型,提出了一种基于周期性排列的金属纳米条带增强石墨烯吸收的等离激元结构,实现了石墨烯在近红外波段的吸收增强.Zhao等[25−27]利用金属深光栅结构激发磁激元共振和表面等离激元共振,在可见光和近红外波段实现了石墨烯对电磁波的吸收增强.微纳结构的引入促进了石墨烯增强吸收结构的小型化,并且在吸收率和波长选择性上都具有很好的效果,但是上述结构也面临着诸如入射电磁波极化方向敏感、深光栅加工难度大等问题.目前关于引入石墨烯磁激元(magnetic polaritons,MPs)共振吸收增强结构后的调制效果鲜有研究.
本文设计了一种金属-绝缘层-金属-石墨烯排列的混合二维浅光栅结构,通过在周期性银纳米阵列结构中激发MPs,达到对入射电磁波能量的局域性增强,通过调整绝缘层及银纳米阵列的几何参数达到调节共振波长的目的.在结构上方铺设石墨烯层,利用下层结构中激发MPs可以实现石墨烯对电磁波的吸收增强.由于石墨烯化学势具有动态可调性,通过外加门控电压改变石墨烯表面的电学特性,可以实现整体结构对入射电磁波吸收的动态可调.金属浅光栅结构设计相对于深光栅结构更加易于工艺的实现,并且高度对称性的结构对入射电磁波的极化方向无限制.基于以上特性,该混合二维浅光栅结构在光电探测、高速光调制领域都具有重要的应用价值.
2 理论模型与计算方法
设计的石墨烯-金属混合二维浅光栅结构如图1(a)和图1(b)所示,该复合结构从下到上依次为银基底、二氧化硅绝缘层、银纳米阵列、石墨烯层;其中银基底足够厚以达到阻隔光子透射;二氧化硅绝缘层厚度为d;银纳米阵列在x,y方向上排列周期,即光栅周期均为p;银纳米单元长度、宽度均为w,单元高度为h.使用多维物理场仿真软件COMSOL对上述结构在近红外波段的吸收和调制特性进行了仿真计算.
在仿真中,二氧化硅绝缘层的折射率为1.45;银的光学参数由德鲁德模型(Drude model)推导的复介电常数εAg表征:
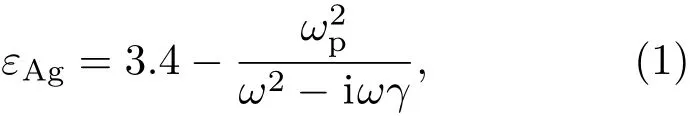
其中,等离子频率ωp=1.39×1016rad/s,衰减速率γ=2.7×1013s−1,ω表示入射光角频率[27].
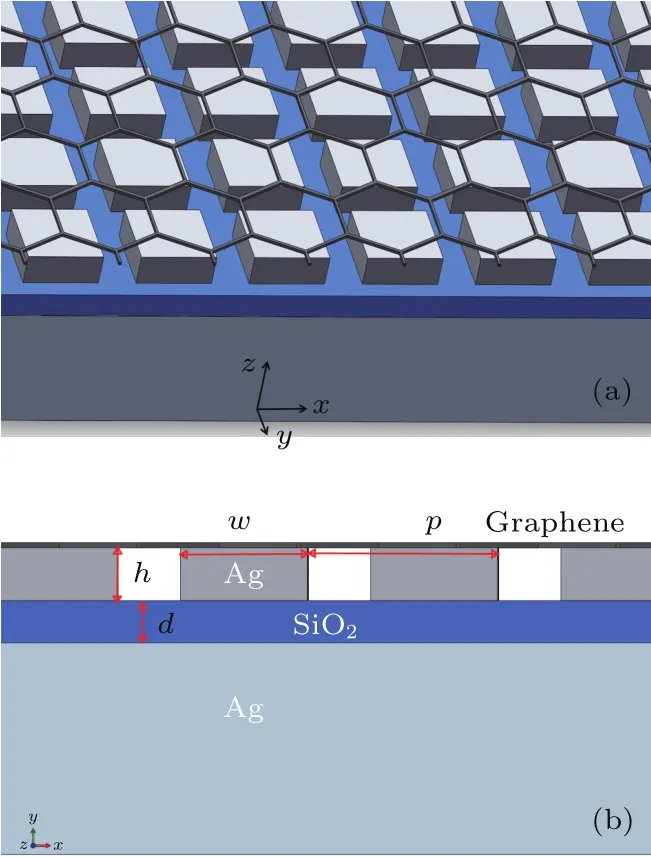
图1 石墨烯-金属二维混合浅光栅结构示意图 (a)结构三维示意图;(b)x方向上四个单元结构的正视图Fig.1.Schematic diagram of the hybrid twodimensional graphene-metal shallow grating structure:(a)Schematic of three-dimensional;(b)the front view of four units structure in x direction.
石墨烯的电导率可以通过随机相位近似 (random-phase approximation,RPA)方法获得[28,29],σg由带间跃迁σinter和带内跃迁σintra组成[30]:
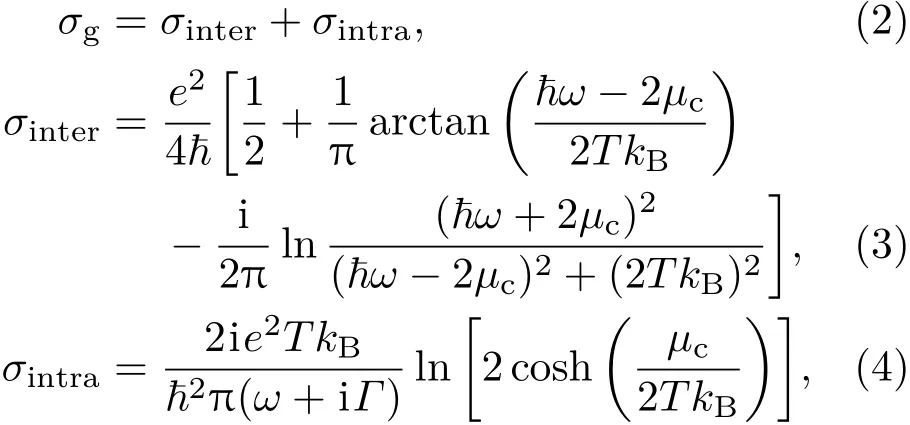
其中~ω表示光子能量,e表示电子电荷量,kB表示玻尔兹曼常数,µc表示石墨烯化学势,Γ表示带电粒子散射率(Γ=1/τ,τ为载流子弛豫时间),T表示开尔文温度.在本文的仿真中限定:T=300 K,τ=0.1 ps.进一步结合石墨烯电导率σg和石墨烯厚度∆,可以得到石墨烯的介电常数[31]:

石墨烯的厚度∆为0.34 nm,在仿真中可以将石墨烯作为表面电流层或薄层处理,两种处理方式的结果完全一致,但考虑到前者可以避免亚纳米级网格所导致的仿真计算量过大的问题,所以在仿真中将石墨烯设置为表面电流层.
通过有限元软件COMSOL可以得出石墨烯-金属混合二维浅光栅结构的电磁响应,并且通过电磁波传输的S参数计算出结构对入射电磁波的吸收率α(λ)=1 −|S11(λ)|2,S11表示S参数中电磁波输入端口的反射系数.
为了说明石墨烯在混合二维浅光栅结构中对增强光吸收所起到的作用,可以计算特定材料对入射电磁波的吸收率.特定位置处的能量散射密度可表示为[25]
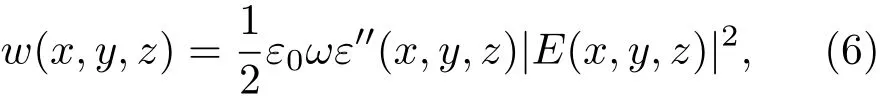
其 中 ε′′(x,y,z)表 示 材 料 介 电 常 数 的 虚 部,E(x,y,z)表示材料覆盖区域某一点的电场强度.对材料覆盖区域进行积分等运算,可以得到特定波长下的材料吸收率:
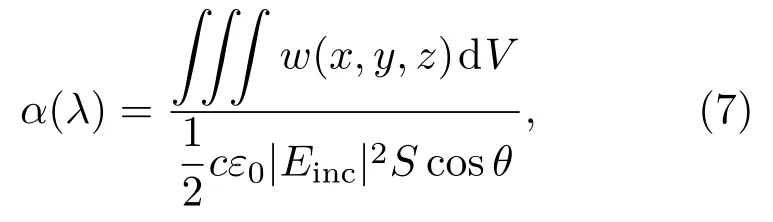
其中分母表示入射电磁波的总能量,c表示真空中的光速,Einc表示入射电磁波电场强度,S cosθ表示入射截面积.
3 计算结果与分析
首先研究了有石墨烯层和无石墨烯层情况下,混合二维浅光栅结构整体对入射电磁波的吸收情况.由于结构在x,y方向上均具有周期性,所以选取一个周期性重复单元进行仿真计算.参照相关文献[23—27]中近红外波段吸收器的尺寸特点,选取结构参数如下:p=180 nm,h=30 nm,w=160 nm,d=10 nm,石墨烯化学势设定为µc=0.3 eV,入射电磁波为TM波,即磁场分量平行于y轴且正入射,入射电磁波能量为1 W,吸收率曲线如图2所示.值得注意的是,由于结构在x,y方向上的对称性,入射TE波也会得到完全相同的结果.
可以发现结构在1480 nm波长处有一个吸收峰,这个吸收峰就是MPs所激发的第一级次共振峰[25],在没有石墨烯层的情况下,吸收率仅为30%.增加石墨烯层后,共振峰位置没有发生改变,同时混合二维浅光栅结构的吸收率提高到了85%,说明石墨烯层具有明显提高结构电磁波吸收率的作用.

图2 有石墨烯和无石墨烯情况下,混合二维浅光栅结构的电磁波吸收率Fig.2.Absorption spectra of the hybrid twodimensional shallow grating structure with graphene and without graphene.
为了说明混合二维浅光栅结构中石墨烯对电磁波吸收率的影响,给出了与图2对应的相同结构尺寸下,1480 nm波长TM波正入射时的磁场分布图和能量损耗图.图3(a)和图3(b)分别为无石墨烯和有石墨烯时结构的磁场分布图,图中箭头表示电场的方向.可以看到磁场主要分布在银纳米阵列单元正下方的二氧化硅绝缘层中,这是由MPs产生的,入射电磁波波长刚好满足混合二维浅光栅结构的共振吸收条件.图中绝缘层两边电场方向相反,即周期性变化的磁场在周围引起了感应电流,说明结构具有很强的抗磁性,这在共振中心波长1480 nm处表现的尤为强烈.值得说明的是,图中箭头方向表示某一瞬态时的电场方向,实际电场方向会随着磁场方向的周期性变化而变化.图3(c)和图3(d)分别为无石墨烯和有石墨烯时结构中能量的分布情况,能量从光栅沟槽进入结构内,可以看到增加石墨烯后银对于电磁波能量的吸收反而减少了,电磁波主要被石墨烯吸收(图中显示石墨烯层处为白色,表明已经超出颜色图例表征的上限),并且吸收位置主要集中在银纳米阵列单元的左右上角处.仿真计算结果显示,在入射电磁波功率为1 W的情况下,入射电磁波在石墨烯处的功率损耗密度最高达到了2.96×1023W/m3,比银覆盖区域的功率损耗密度峰值高出了两个数量级.结合图2中的仿真结果,无石墨烯时整体结构吸收率为30%,有石墨烯时结构吸收率为85%,也就是说,在MPs激发的情况下,局部电磁波能量的聚集使得石墨烯至少吸收了入射电磁波能量的55%,这个吸收率是石墨烯悬空状态下在近红外波段吸收率的近24倍.
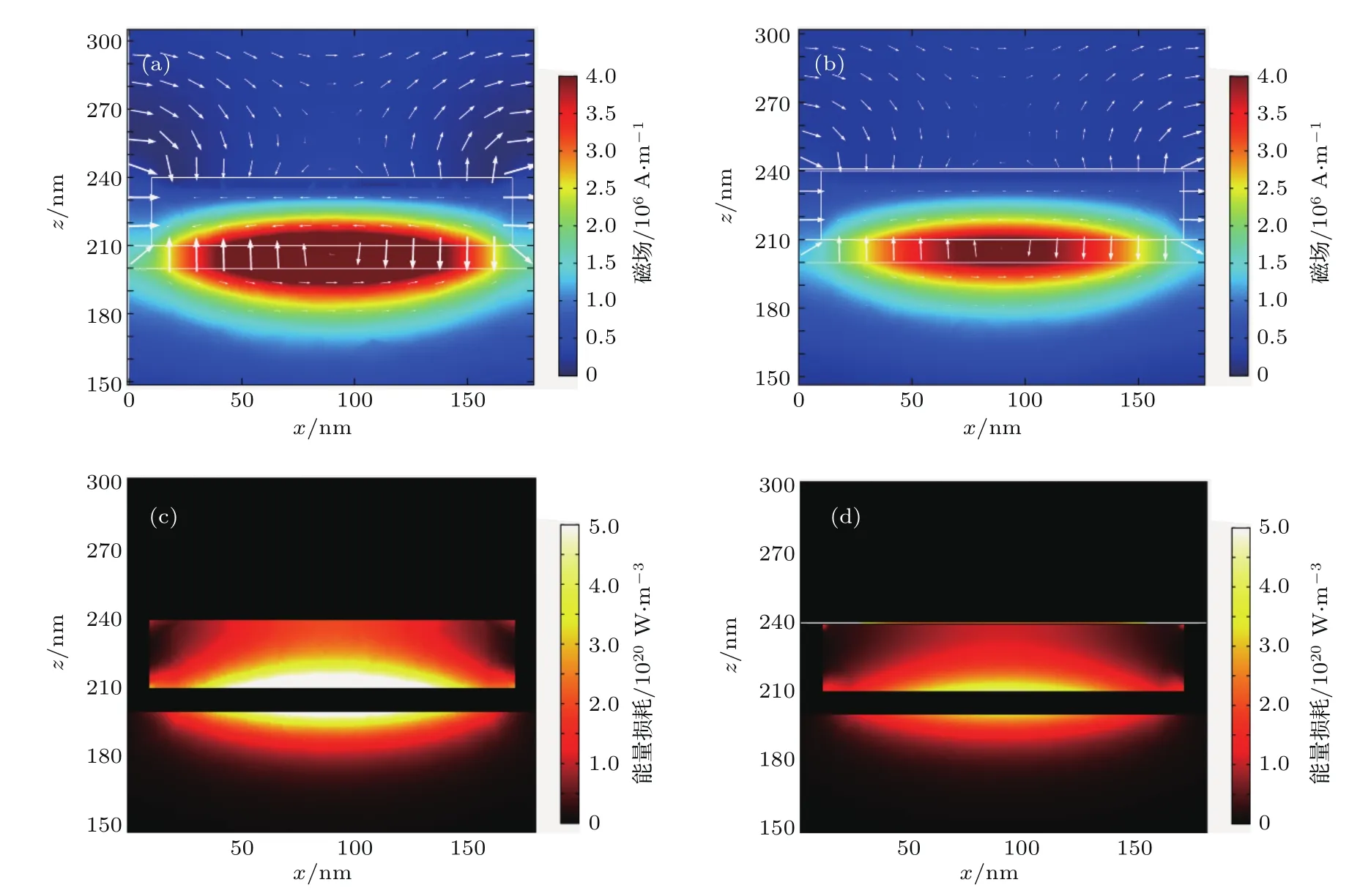
图3 磁场分布与能量损耗分布 (a)无石墨烯时的磁场分布图;(b)有石墨烯时的磁场分布图;(c)无石墨烯时的能量损耗分布图;(d)有石墨烯时的能量损耗分布图Fig.3.Magnetic fi eld distribution and power dissipation profi les:(a)Magnetic fi eld of the structure without graphene;(b)magnetic fi eld of the structure with graphene;(c)power dissipation profi le of the structure without graphene;(d)power dissipation profi le of the structure with graphene.
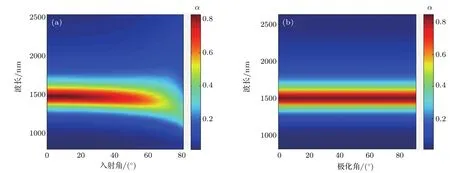
图4 TM波入射角度从0◦变化到80◦(a),极化角度从0◦(TM波)变化到90◦(TE波)的情况下(b),混合二维浅光栅结构的电磁波吸收率与波长的关系Fig.4.Relationship between electromagnetic wave absorptivity and wavelength of the hybrid two-dimensional shallow grating structure:(a)For diff erent incidence angles of TM from 0◦ to 80◦;(b)for diff erent polarization angles from 0◦(TM)to 90◦(TE).
为了说明混合二维浅光栅结构对非正入射电磁波的吸收效果,还计算了不同入射角和极化方向下结构对电磁波的吸收率.结构参数为p=180 nm,h=30 nm,w=160 nm,d=10 nm,石墨烯化学势设定为µc=0.3 eV.图4(a)为入射角度从0◦增加到80◦时结构的吸收情况,可以发现小角度入射情况下,混合二维浅光栅结构的电磁波吸收率对入射角度的依赖性不明显,并且共振波长不会发生明显的改变.如图所示,正入射时在1480 nm处达到85%的吸收峰值;当入射角度为10◦时,共振波长为1470 nm,对应的吸收峰值为84%.进一步增加入射角度到60◦,结构吸收率峰值仍保持在60%以上.这与混合二维浅光栅结构激发MPs增强吸收的原理相符合,前述提到MPs的激发主要是由电磁波的磁场分量决定的,所以通过改变TM波的入射角度并不会改变其磁场分量的方向和大小,也就不会对结构MPs的激发情况产生较大的影响.图4(b)为不同极化角正入射下,混合二维浅光栅结构的电磁波吸收率与波长的关系.由于结构在x,y方向上具有高度对称性,所以当极化角由0◦(TM波)变化到90◦(TE波)时,结构的电磁波吸收特性并没有发生明显改变.
混合二维浅光栅结构的几何参数对结构的吸收效果会产生影响.图5(a)显示了在结构参数为p=180 nm,h=30 nm,w=160 nm,石墨烯化学势µc=0.3 eV的情况下,不同的绝缘层厚度d对应的吸收率曲线.可以看到随着绝缘层厚度的增加,结构对电磁波的吸收率减小,吸收曲线半高全宽增加,当绝缘层厚度为5 nm时,吸收率为91%,半高全宽为230 nm,当绝缘层厚度增加到20 nm时,结构的吸收率下降到了79%,半高全宽增加到360 nm.这是因为当绝缘层厚度增加时,混合二维浅光栅结构中银纳米阵列单元与银基底之间对于入射电磁波能量的耦合作用减弱,导致结构对于光的局部增强效果减弱,影响了石墨烯及银对电磁波能量的吸收效果,也使结构对共振波长的选择性降低.同时,随着绝缘层厚度由5 nm增加到20 nm,吸收峰对应波长也由1760 nm移动到了1400 nm处,即吸收峰的位置发生了明显的蓝移,这个可以利用混合二维浅光栅的等效RLC电路模型中进行预测.
等效RLC电路模型是在预测分析超材料表面结构对电磁波响应特性中经常用到的一种方法,尤其可以直观地解释结构几何参数变化对于电磁吸收的影响,假定Z0=为真空中的本征阻抗,根据有效介质近似理论[32],原则上当结构等效电路的等效阻抗Z(ω)=Z0时,结构达到共振条件,对入射波长的吸收率最大.图5(b)为图1中混合二维浅光栅结构单元的等效电路模型.当入射波(考虑TM波)照射到结构的表面时,入射波的磁场分量与银纳米阵列单元在y方向平行,根据楞次定律,周期性变化的磁场分量将在光栅沟槽周围产生感应电流,继而会激发感应磁场.在这个过程中,绝缘层的存在使银纳米阵列单元和银基底之间产生电容效应,等效电容为C,电容的大小由几何参数、中间介质的介电常数和金属表面的电子分布情况决定.银纳米阵列及银基底作为导体,本身及相互之间均具有电感效应,假设银阵列单元的自感和互感分别为Lm1,Le1,银基底的自感和互感分别为Lm2,Le2,石墨烯并不改变混合二维浅光栅结构的共振波长,所以视作一个电阻Rg,这是一个典型的RLC回路模型.当入射波频率与该结构的电路模型的固有频率相等时,能量的共振使整个结构可以实现对入射波能量的强烈吸收.在RLC回路中,谐振波长λ ∝ 2πc且与电阻Rg无关.考虑到C,Lm1,Le1,Lm2,Le2的大小与结构的几何参数密切相关,可以通过设计结构的几何参数达到调整谐振波长的目的.图1结构中当绝缘层厚度增加而其他参数不变时C将减小,即吸收峰波长将发生蓝移,并且变化趋势会随着绝缘层厚度增加而放缓.
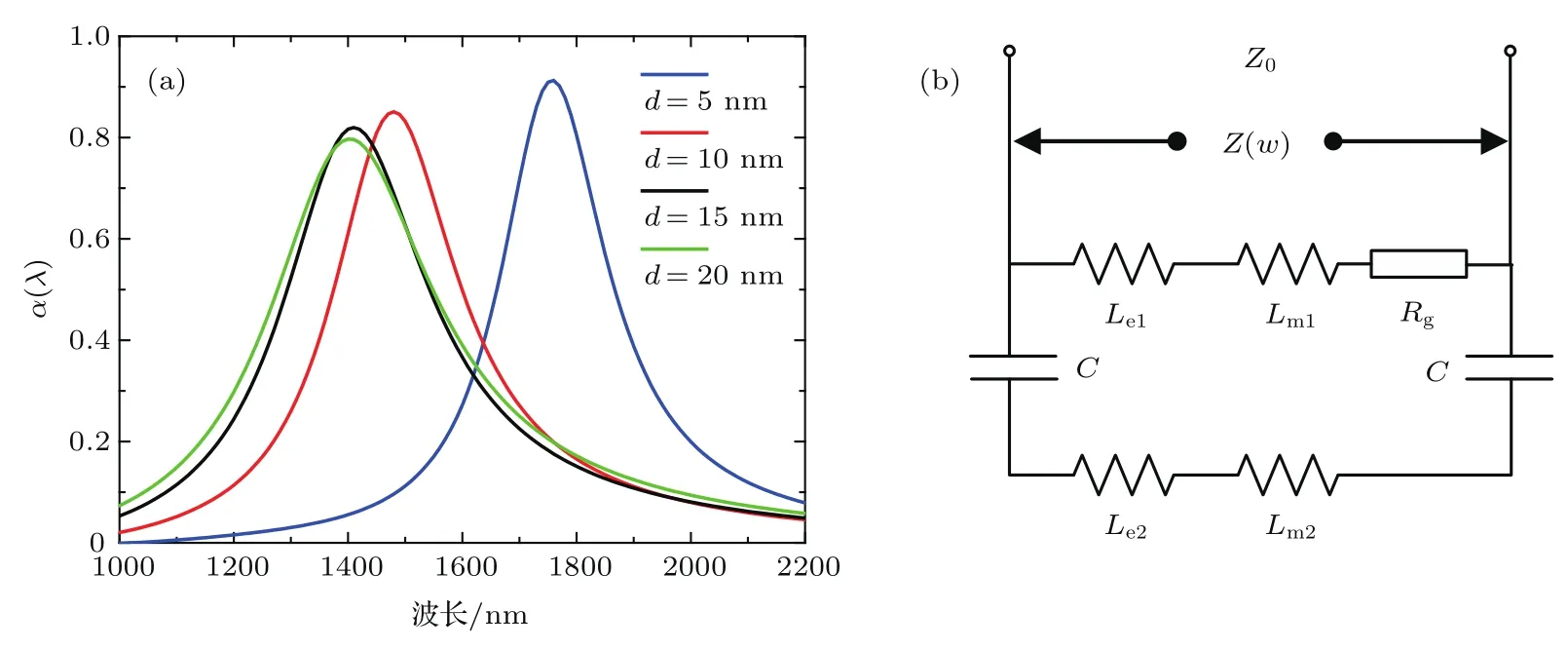
图5 不同绝缘层厚度下混合二维浅光栅结构的吸收率图(a)和混合二维浅光栅结构等效电路图(b)Fig.5.Absorption spectra of the hybrid two-dimensional shallow grating structure with diff erent thicknesses of the dielectric layer(a)and equivalent circuit for the hybrid two-dimensional shallow grating structure(b).
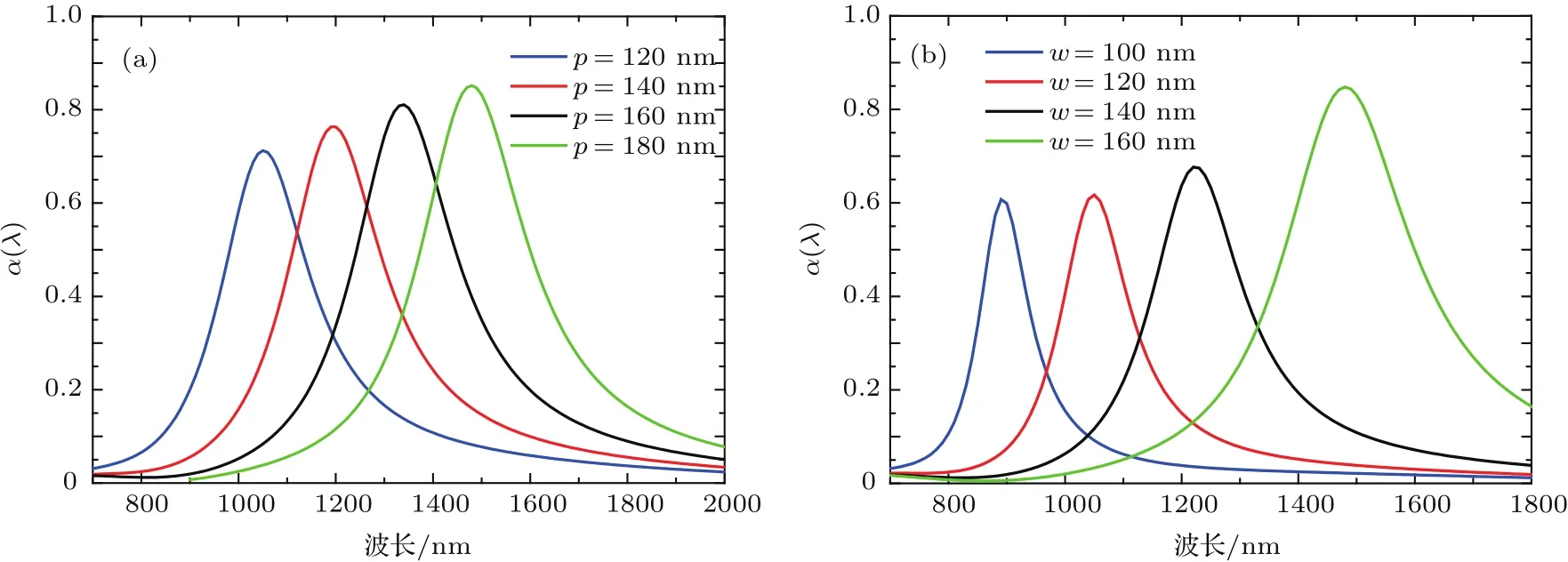
图6 混合二维浅光栅结构电磁波吸收率与光栅周期(a)及银纳米阵列单元宽度(b)的关系Fig.6.Absorption spectra of the hybrid two-dimensional shallow grating structure for(a)diff erent grating periods;(b)diff erent width of unit silver nanoparticles.
本文又分别研究了结构中光栅周期和银纳米阵列单元宽度对电磁波吸收率的影响,图6(a)为结构参数p−w=20 nm,h=30 nm,d=10 nm情况下,混合二维浅光栅周期p由180 nm依次递减到120 nm时分别对应的吸收率;图6(b)为结构参数p=180 nm,h=30 nm,d=10 nm情况下银纳米阵列宽度w由160 nm依次递减到100 nm时分别对应的吸收率.研究表明,随着光栅周期和银纳米阵列单元宽度的减小,混合二维浅光栅结构的吸收峰中心波长均会出现明显蓝移,这也与上述等效电路模型的分析结果相一致.若以F=w/p表示银纳米阵列的空占比,当保持p-w值不变时,随着光栅周期p和银纳米阵列单元宽度w的减小,F的值也将减小,这就导致了银纳米阵列与银基底之间能产生电容效应的有效面积减小,共振波长出现蓝移.同时在结构中,石墨烯对电磁波能量的吸收效果也与占空比有很大的关联,根据图3(d)可以看出,石墨烯对能量的吸收主要集中在银纳米阵列单元的上角,随着占空比的减小,单位面积内银纳米阵列分布密度减小,所以石墨烯对能量的吸收能力减弱,结构整体的吸收效果也会受到影响.
石墨烯的光学特性可以通过改变其化学势实现动态可调,通过外加门控电压或者化学掺杂,石墨烯在光传输上可以实现介质特性和金属特性的转换.基于石墨烯的这一特点,又进一步研究了改变石墨烯化学势µc对混合二维浅光栅结构吸收特性的影响.图7(a)为p=180 nm,w=120 nm,d=10 nm,h=30 nm时混合二维浅光栅结构在不同µc下的吸收曲线.可以发现µc对于结构吸收率具有很好的调控作用,当石墨烯化学势µc=0.1 eV时,结构在中心波长1040 nm处达到吸收峰值62%,当0.1 eV<µc<0.5 eV时,结构的吸收并没有明显变化,而当µc=0.6 eV时,结构吸收率出现了明显的变化,之后随着µc的进一步增加吸收率继续下降.值得注意的是,µc对混合二维浅光栅结构吸收特性的调制并不影响由MPs决定的共振吸收波长.根据(6),(7)式可知,石墨烯对入射电磁波的吸收调控作用与石墨烯表面介电常数的虚部ε′′有关.图7(b)给出了石墨烯介电常数虚部关于石墨烯化学势及入射波长的变化关系.由图7(b)可以看出,当入射波长一定时,随着化学势的增加,ε′′开始缓慢减小,直到µc≈~ω/2时变化趋势出现了明显的拐点,当µc>~ω/2时,ε′′的值急剧减小. 这是因为在近红外波段,入射电磁波能量相对较大,因此石墨烯的带内跃迁和带间跃迁都参与了石墨烯与电磁波相互作用.但是当µc>~ω/2时,石墨烯的带内跃迁在石墨烯与电磁波相互作用中占主导地位,带间跃迁可以忽略不计.这也就导致了石墨烯介电常数虚部ε′′的急剧减小.可以很容易计算出λ=1040 nm时对应的µc≈0.6 eV,这刚好与图7(a)中的结果相一致.
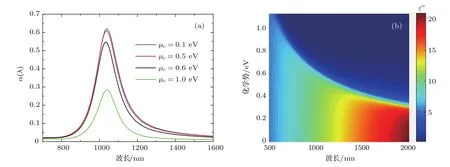
图7 不同石墨烯化学势下,混合二维浅光栅结构电磁波吸收率(a)和以化学势和入射波长为变量的石墨烯介电常数虚部ε′′(b)Fig.7.Absorption spectra of the hybrid two-dimensional shallow grating structure in diff erent chemical potentials of graphene(a)and imaginary parts of dielectric constant of graphene with variable chemical potential and incident wavelength(b).
由于研究的混合二维浅光栅结构具有零透射的特点,所以结构对入射电磁波的反射率可以表示为R(λ)=1−α(λ),其中α(λ)为S参数计算的电磁波吸收率.利用1−R1/R2来计算特定波长下的调制深度,其中R1,R2分别表示µc=0.1 eV和µc=1 eV时的反射率. 基于此得到了当p=180 nm,h=30 nm,d=10 nm时,不同金属纳米颗粒宽度的情况下石墨烯化学势µc对于混合二维浅光栅结构反射率的调制效果,如图8所示.通过计算得出,在w为120,100,80 nm时,通过调控石墨烯化学势µc由0.1 eV变化到1 eV,结构对光的反射调制深度分别为54.8%,50.3%,46.8%.
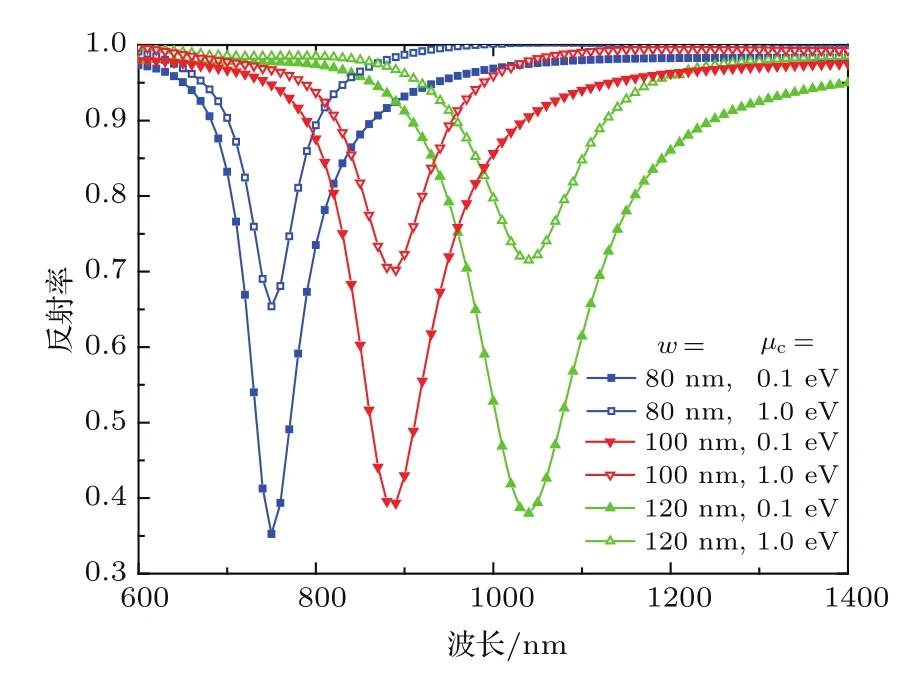
图8 不同银纳米单元宽度w的情况下,µc从0.1 eV变化到1 eV时对于混合二维浅光栅结构的反射调制效果.Fig.8.Modulation of optical refl ectance in the hybrid two-dimensional shallow grating structure as a function of w,whereµc is changed from 0.1 eV to 1 eV.
4 结 论
本文设计了一种金属-绝缘层-金属-石墨烯的混合二维浅光栅结构,并通过有限元仿真计算和等效电路模型分析预测相结合的方式,研究了该结构中石墨烯的吸收增强效应.在光栅周期p=180 nm,银纳米单元宽度w=160 nm,单元高度h=30 nm,绝缘层厚度d=10 nm的情况下,石墨烯层的增加使结构的吸收峰值在1480 nm处由30%提高到了85%,实现了石墨烯在近红外波段24倍左右的吸收增强;结构的吸收特性对入射角度依赖性不强,并且由于具有二维方向上的对称性,该结构对入射电磁波的极化方向没有特殊要求;分析了结构尺寸与磁激元共振效应的关系,当光栅周期p、银纳米单元宽度w、绝缘层厚度d减小时,均会导致共振波长的蓝移;最后研究了石墨烯化学势对于结构吸收率的动态可调特性,通过调控石墨烯化学势由0.1 eV变化到1 eV,可以实现54.8%的反射调制深度.基于石墨烯优异的光电特性,该结构的吸收增强和吸收率动态可调特性在光电探测、太阳能电池和光电调制领域具有较高的应用价值,并且简洁的浅光栅结构和低成本的材料更加易于工艺实现.
[1]Geim A K,Novoselov K S 2007 Nat.Mater.6 183
[2]Neto A H C,Guinea F,Peres N M R 2009 Rev.Mod.Phys.81 109
[3]Bonaccorso F,Sun Z,Hasan T,Ferrari A C 2010 Nat.Photon.4 611
[4]Bolotin K I,Sikes K J,Jiang Z,Klima M,Fudenberg G,Hone J 2008 Solid State Commun.146 351
[5]Xia F N,Mueller T,Lin Y M,Valdes-Garcia A,Avouris P 2009 Nature Nanotech.4 839
[6]Bao Q,Loh K P 2012 ACS Nano 6 3677
[7]Nair R R,Blake P,Grigorenko A N,Novoselov K S,Booth T J,Stauber T,Peres N M R 2008 Science 320 1308
[8]Hong B H 2009 Nature 457 706
[9]Liu W Z,Wang W,Xu H Y,Li X H,Yang L,Ma J G,Liu Y C 2015 Appl.Phys.Lett.8 095202
[10]Horng J,Chen C F,Geng B S,Girit C,et al.2012 Phys.Rev.B:Condens.Matter 83 165113
[11]Li E P,Chu H S,Wu L,Koh W S 2010 Opt.Express 18 14395
[12]Zhang H Y,Huang X Y,Chen Q,Ding C F,Li T T,Lü H H,Xu S L,Zhang X,Zhang Y P,Yao J Q 2016 Acta Phys.Sin.65 018101(in Chinese)[张会云,黄晓燕,陈琦,丁春峰,李彤彤,吕欢欢,徐世林,张晓,张玉萍,姚建铨2016物理学报65 018101]
[13]Alaee R,Farhat M,Rockstuhl C,Lederer F 2012 Opt.Express 20 28017
[14]Ju L,Geng B,Horng J,Girit,Martin M 2011 Nature Nanotech.6 630
[15]Thongrattanasiri S,Koppens F H,Garcia de Abajo F J 2012 Phys.Rev.Lett.108 047401
[16]Gao W,Shi G,Jin Z,Shu J,Zhang Q 2013 Nano Lett.13 3698
[17]Marco F,Alexander U,Andreas P,Govinda L,Karl U,Hermann D,Pavel K,Asron M A,Werner S,Gottfried S,Thomas M 2012 Nano Lett.12 2773
[18]Liang Z J,Liu H X,Niu Y X,Yin Y H 2016 Acta Phys.Sin.65 138501(in Chinese)[梁振江,刘海霞,牛燕雄,尹贻恒2016物理学报65 138501]
[19]Maillard M,Huang P,Brus L 2003 Nano Lett.3 1611
[20]Zhao B,Wang L,Shuai Y,Zhang Z M 2013 Int.J.Heat Mass Transfer 67 637
[21]Zhao J M,Zhang Z M 2015 J.Quant.Spectrosc.Radiat.Transfer 151 49
[22]Fang Z,Wang Y,Liu Z,Schlather A,Ajayan P M,Koppens F H,Nordlander P,Halas N J 2012 ACS Nano 6 10222
[23]Cai Y J,Zhu J F,Liu Q H 2015 Appl.Phys.Lett.106 043105
[24]Cai Y J,Zhu J F,Liu Q H,Lin T,Zhou J Y,Ye L F,Cai Z P 2015 Opt.Express 23 32318
[25]Zhao B,Zhao J M,Zhang Z M 2015 J.Opt.Soc.Am.B:Opt.Phys.32 1176
[26]Zhao B,Zhao J M,Zhang Z M 2014 Appl.Phys.Lett.105 031905
[27]Zhao B,Zhang Z M 2014 J.Quant.Spectrosc.Radiat.Transfer 135 81
[28]Wunsch B,Stauber T,Sols F,Guinea F 2006 New J.Phys.8 318
[29]Hwang E H,Sarma S D 2007 Phys.Rev.B 75 205418
[30]Falkovsky L A 2008 J.Phys.Conf.Ser.129 012004
[31]Vakil A,Engheta N 2011 Science 332 1291
[32]Landy N I,Bingham C M,Tyler T,Jokerst N,Smith D R,Padilla W J 2009 Phys.Rev.B:Condens.Matter 79 125104
