各向异性表面张力对定向凝固中共晶生长形态稳定性的影响∗
2018-06-19徐小花陈明文王自东
徐小花 陈明文† 王自东
1 引 言
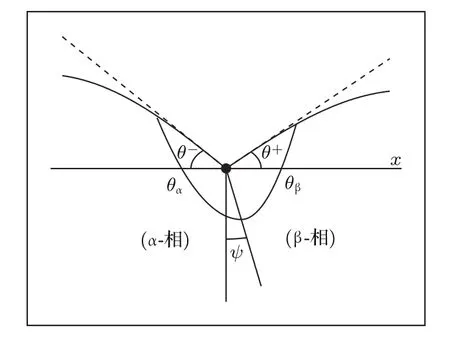
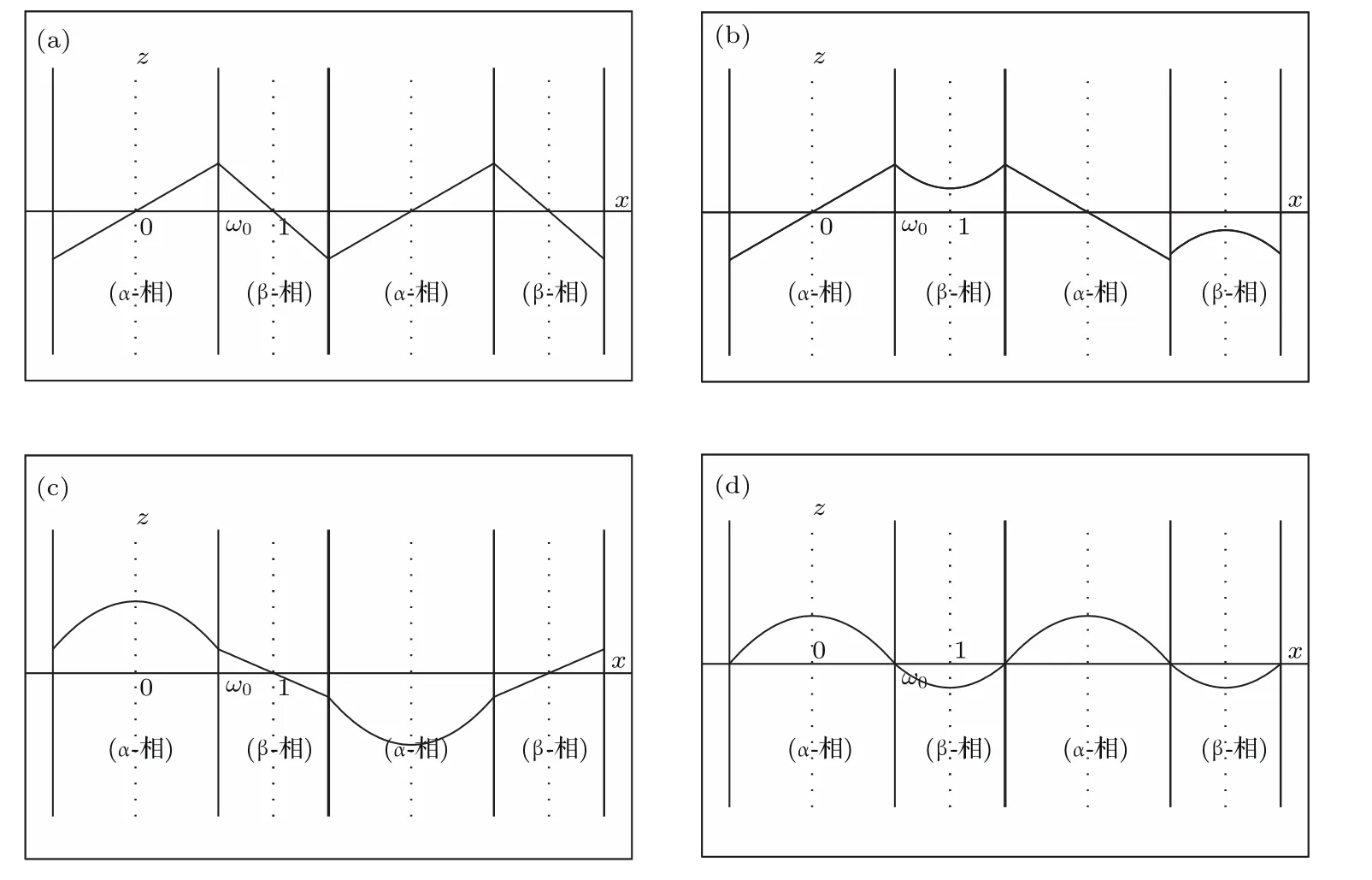
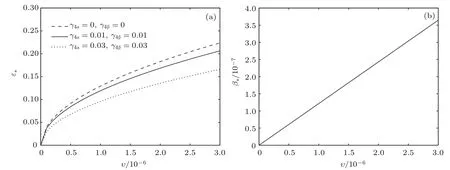
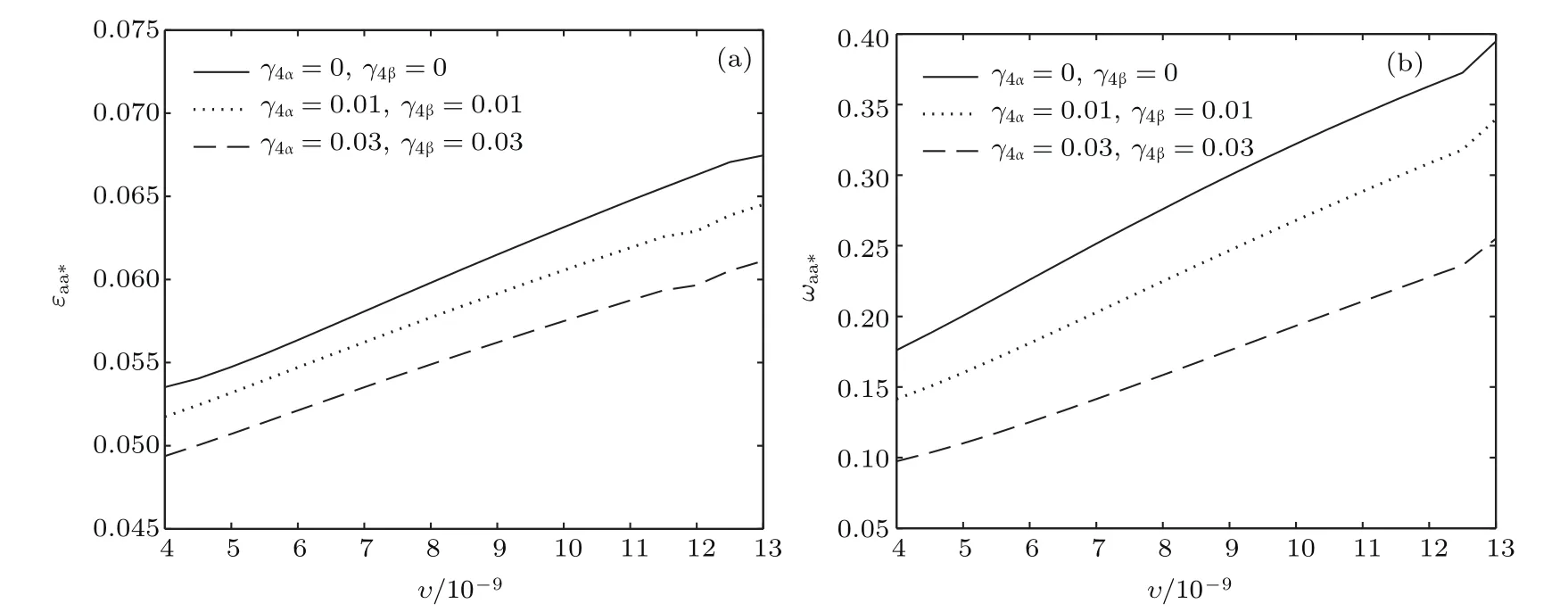
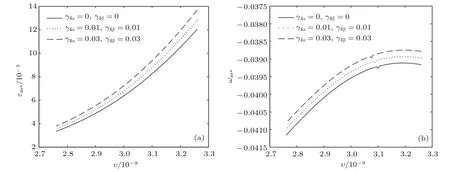
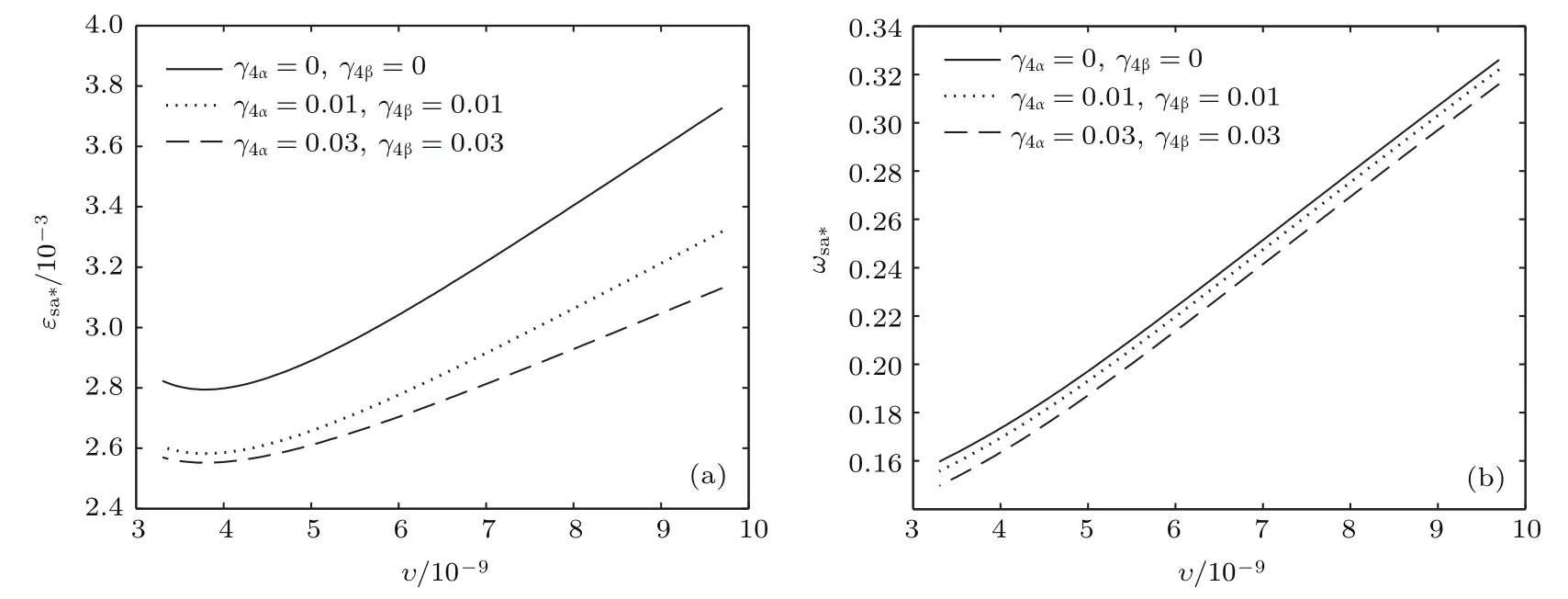
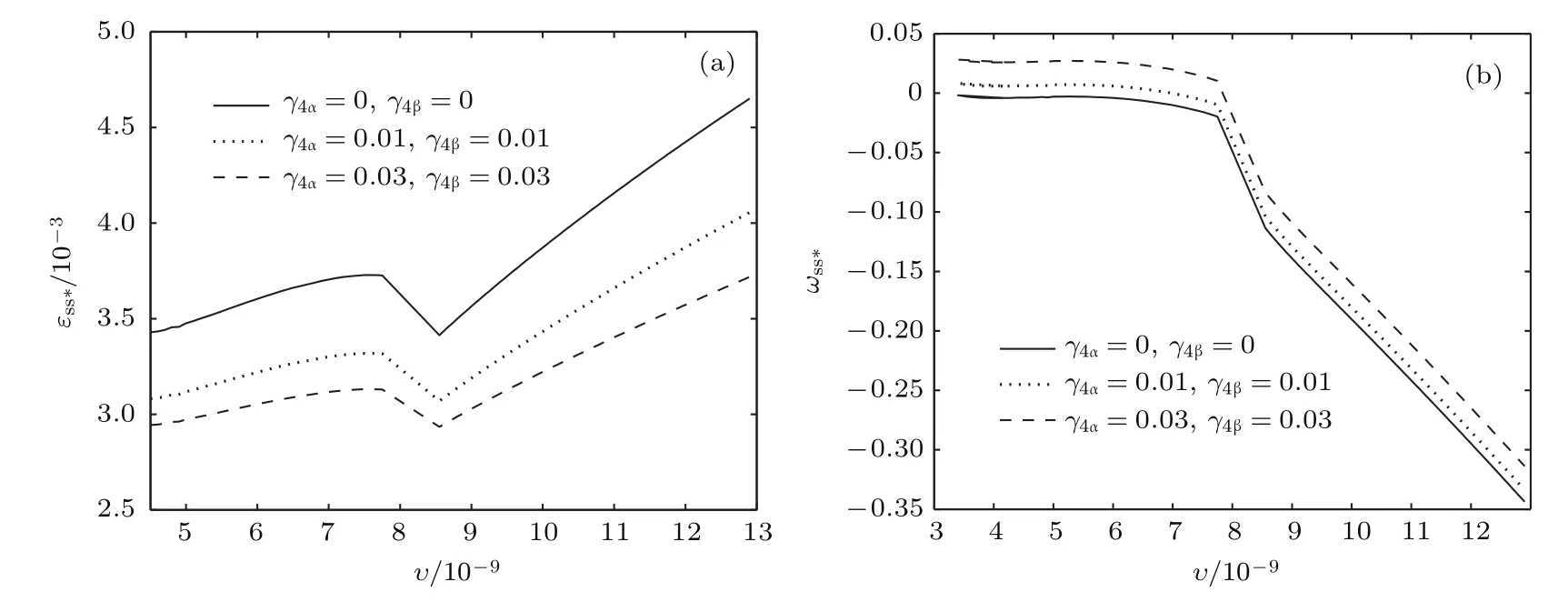
共晶界面形态稳定性是凝聚态物理学和材料科学的一个基础课题[1−6].定向凝固过程中晶体形态的不稳定性可能会导致不同的微观结构,最终极大地影响产品的物理和机械性能.Hele-Shaw生长室是观察共晶定向凝固过程的典型实验装置,它是一个封存有样品材料的十分扁平的容器.生长室设置了一个高温区与一个低温区,高温区的温度设为TH,低温区的温度为TC,材料的凝固温度TM介于两者之间:即TC 固体材料本身并非各向同性介质,其晶格结构使固体体内的物理量以及表面的物理参数依赖于取向,变为各向异性量.固体材料这些物理参量的各向异性特征对凝固过程动力学与界面稳定性机理以至对界面微结构图案的形成与选择造成重要的影响[14].王志军等[15,16]研究了各向异性表面张力对定向凝固过程中初始平界面稳定性的影响,发现各向异性表面张力的非线性效应导致界面倾斜生长.Chen等[17]研究了各向异性表面张力对定向凝固过程中球晶生长的影响,发现在各向异性表面张力作用下,球晶生长初始阶段部分界面首先向内移动,达到一定的熔化深度后向外移动.Xu[18]研究了各向异性表面张力对定向凝固过程中枝晶生长的影响,发现当存在各向异性表面张力时,枝晶系统具有两种不同的整体不稳定性机理:震荡不稳定性与低频不稳定性.陈明文等[19]研究了各向异性表面张力对定向凝固过程中深胞晶生长的影响,发现当各向异性表面张力增大时,深胞晶界面全长增大,根部低端的曲率半径增大.本文应用多重变量展开法研究各向异性表面张力条件下定向凝固共晶生长形态稳定性,揭示了各向异性表面张力对共晶生长不稳定性区域大小的影响. 图1 共晶结构的示意图Fig.1.Schematic diagram of the eutectic structure. 假设由α和β两相组成的片层共晶以拉度V向液相稳定推进,共晶片层与固-液界面垂直.选取固-液界面处α相片层的中心为坐标原点,x轴与片层垂直,z轴与晶体生长方向平行,如图1所示.共晶界面用函数z=h(x,t)表示,它也是共晶生长解的一部分. 本文引用Xu等[12]的无量纲化尺度,并且假设主间距的一半ℓw远小于溶质扩散长度ℓD=κD/V,即ℓw≪ ℓD,其中κD为溶质扩散系数. 选取ℓw为长度尺度,V为速度尺度,ℓw/V为时间尺度,∆H/(cPρL)为温度尺度,Ce为浓度尺度,其中∆H是单位体积内固相潜热,cP是比热容,ρL是溶质密度,Ce是共晶浓度.无量纲温度¯T=(T−Te)/[∆H/cPρL],无量纲浓度¯C=(C−Ce)/Ce,无量纲无穷远处浓度¯C∞=[(C∞)D−Ce]/Ce,其中Te是共晶温度,(C∞)D是有量纲无穷远处浓度.为了书写简洁起见,下文省略掉无量纲量头上的符号“-”.各向异性表面张力用四重对称函数γ(θ)= γ0[1+ γ4cos(4θ)][14]表示,其中γ0为各向同性表面张力系数,γ4为各向异性表面张力系数,θ为界面法向量与z轴之间的夹角.共晶生长系统还包含以下无量纲量:Peclet数Pe= ℓw/ℓD;形态参数M=(−mCe)/[∆H/(cPρL)],m 是液相线系数;界面稳定性参数Γ = ℓc/ℓw,ℓc是毛细长度,ℓc= γ0cPρLTe/(∆H)2; 无量纲温度梯度G=(G)Dℓw/[∆H/(cPρL)],(G)D是与实验装置相关的有量纲温度梯度;无量纲间距参数Wc=wc/ℓw,wc表示α相宽度的一半. 注意到γ0,γ4,m和分离系数κ都是分段常值函数,在α相和β相都有各自对应的常数值.用q来代表这类物理量,qα表示其在α相的函数值,qβ表示其在β相的函数值.由于溶质扩散长度ℓD远小于热扩散长度ℓT= κT/V,即ℓD≪ ℓT,其中κT是热扩散系数.界面温度可以近似表示为TL=TS∼ G(z−z∗),其中TL,TS分别是液相和固相温度,z∗是与α相尖端位置有关的常数.对于典型的实验材料,Peclet数Pe很小.以CBr4-C4Cl6[20,21]生长系统为例,Pe≈0.01,Γ≈2.5×10−5.为了做渐近分析,本文把Peclet数Pe作为基本的小参数,假设ε=Pe≪ 1且Γ=ε2¯Γ,¯Γ=O(1). 为考察共晶生长形态稳定性,利用共晶生长的定常解作为基态进行稳定性分析.在初始时刻t=0时对基态解做一小扰动,并将在t>0以后形成的非定常解分解成两个部分: 其中{CB,hB}是系统的基态,{e C,˜h}是系统的扰动态.假设初始扰动态的范数共晶生长系统的定常解为[11]: 其中 θ−是α相的接触角,θ+是β相的接触角,这两个接触角与夹度θα,θβ以及倾斜角ψ之间满足关系式θ−= θα−π/2−ψ,θ+= θβ−π/2+ψ,如图2所示. 图2 三相点附近的界面示意图Fig.2.A sketch of the interface shape near the triple point. 将系统方程以振幅远小于1进行线性化处理,结合(1)式—(4)式,可以得到共晶生长系统的扰动态满足以下控制方程和边界条件: 1)在远场区域,当z→∞时, 2)在侧壁x=0和x=1上, (b)反对称(antisymmetric)模式(A-模式) 3)在界面z=hB上, (a)Gibbs-Thomson条件 (a)对称(symmetric)模式(S-模式) 由三角诱导公式可知, 于是有 结合(9)式和(10)式,Gibbs-Thomson条件可以改写为 (b)杂质质量守恒条件 为了得到系统扰动态的渐近解,引入快变量[12] 按照多重变量(x,z,x+,z+,t+),解可以写成如下形式: 并对波数函数和特征值做如下展开: 将(13)式—(17)式代入到方程和边界条件(5)式—(12)式,可以得到系统在零级近似下的控制方程和边界条件为 1)在远场区域,当z→∞时, 2)在侧壁x=0和x=1上, (a)S-模式 (b)A-模式 3)在界面z=0或z+=0上, (a)Gibbs-Thomson条件 (b)杂质质量守恒条件 其中ˆΘ(x)为分段常值函数,ˆΘα=1,ˆΘβ=−ˆκ. 4)三相点处的连接条件,当x=w0时, 上述共晶生长系统有如下零级近似模式解[12]: 其中系数ˆD0是一个任意的复常数.记ˆA0(x)=˜A0(x,0),将模式解(25)式和(26)式代入到界面条件(22)式和(23)式中,得到 该系统存在非零解的条件是方程的系数行列式为零,此条件给出了一个局部的色散关系式: 其中 局部色散关系式(29)是定向凝固中,对于平直界面情形的Mullins-Sekerka公式[22]的推广.当γ4=0,ψ=0时,(29)式变为 (31)式与文献[12]中给出的(10)式相同.对于任意给定的参数σ0,从色散关系式(29)中可以解出3个波函数: 其中 当γ4=0,ψ =0时,(32)式变为 其中 (33)式与Xu等[12]给出的(12)式相同. 这3个波函数{(x),(x),(x)}分别给出了系统3个基本的波动形式解{H1,H2,H3}.在这3个解中,波数函数(x)对应的波动形式解H2必须排除掉,因为当z+→∞时,浓度场的扰动振幅将指数增长,这是不合理的.有物理意义的解只有H1和H3.对于任意固定的点,在ε→0的极限条件下扰动态的一般解必定是解H1与解H3的线性迭加.从而,界面函数外部区域的通解可用这两个基本界面行波的组合表示: 其中系数是待定常数. 浓度场满足的一级近似控制方程和边界条件为: 1)在远场区域,当z→∞时, 2)在侧壁x=0和x=1上, (a)S-模式 (b)A-模式 3)在界面z=0或z+=0上, (a)Gibbs-Thomson条件 (b)杂质质量守恒条件 上述浓度场的一级近似系统是非齐次的,它允许以下形式的模式解: 其中系数ˆD1是一个任意的复常数.记ˆA1(x)=˜A1(x,0),将模式解(41)式和(42)式代入到界面条件(39)式和(40)中,整理得 其中 由于(43)式和(44)式构成的非齐次线性系统的系数行列式为零,故{ˆA1,ˆD1}存在非零解的充分必要条件为 (47)式给出了共晶生长系统的可解性条件: 从方程(43)式—(48)式得到如下公式: 为了得到全局模式解,界面函数的通解必须在三相点x=w0处满足连接条件,在侧壁x=0和x=1处满足侧壁条件.由于局部解在α相和β相是反对称的(A-)或者是对称的(S-),存在着四种不同的组合方式,因此共晶生长系统允许四种类型的全局模式解,即AA-,AS-,SA-和SS-模式,如图3所示.在图3(a)中,全局解在α相和β相均是反对称的,称之为AA-模式,即:当x=0时,˜hα=0; 当x=1时,˜hβ=0. 在图3(b)中,全局解在α相是反对称的,而在β相是对称的,称之为AS-模式,即: 当x=0时,˜hα=0;当x=1时,∂˜hβ/∂x=0. 在图3(c)中, 全局解在α相是对称的,而在β相是反对称的,称之为SA-模式,即:当x=0时,∂˜hα/∂x=0;当x=1时,˜hβ=0.在图3(d)中,全局解在α相和β相均是对称的,称之为SS-模式,即: 当x=0时,∂˜hα/∂x=0;当x=1时,∂˜hβ/∂x=0. 1)全局AA-模式 全局解在三相点处满足连接条件,在侧壁上满足侧壁条件: 图3 扰动系统的四种振动模式 (a)AA-模式;(b)AS-模式;(c)SA-模式;(d)SS-模式Fig.3.Sketch of the perturbed system by four vibration systems connected with a mass:(a)AA-modes;(b)AS-modes;(c)SA-modes;(d)SS-modes. 将解(34)式代入到方程(50)式和(51)式中,常数满足以下方程组: 从方程组(52)—(55),得到 其中 对于全局AA-模式,特征值σ0满足以下量子化条件: 其中Ξ =(cosθ−/cosθ+)2. 2)全局AS-模式 全局解在三相点处满足连接条件,在侧壁上满足侧壁条件: 将解(34)式代入到方程(60)式和(61)式中,化简整理后得 对于全局AS-模式,特征值σ0满足以下量子化条件: 3)全局SA-模式 全局解在三相点处满足连接条件,在侧壁上满足侧壁条件: 将解(34)式代入到方程(65)式和(66)式中,化简整理后得 对于全局SA-模式,特征值σ0满足以下量子化条件: 4) 全局SS-模式 全局解在三相点处满足连接条件,在侧壁上满足侧壁条件: 将解(34)式代入到方程(70)式和(71)式中,化简整理后得 对于全局SS-模式,特征值σ0满足以下量子化条件: 由量子化条件可以看出特征值σ0是关于参数ε和γ4的隐函数.任意给定参数ε和γ4,可以得到一个复数值σ0. 为了更好地阐明生长条件对共晶生长系统的影响,引入无量纲参数[11,12]υ = ℓc,αV/κD, 它反映拉速V 的大小;ˆβ=−ℓc,α(G)D/mαCe,它反映温度梯度(G)D的大小.通过化简可以知道,υ=ε3¯Γα,ˆβ=υG/M.本文采用与Xu[23]研究枝晶的形态稳定性相似的方法,对于四种震荡模式得到各自对应的稳定临界值εaa∗, εas∗, εsa∗和εss∗. 共晶生长系统稳定的选择判据为: 当ε>ε∗,min,共晶生长系统是不稳定的; 当ε6ε∗,min,共晶生长系统是稳定的. 共晶生长系统稳定的选择性条件为: 1)全局稳定模式 给定生长条件,令量子化条件(59)式、(64)式、(69)式和(74)式中特征值σ0=0,发现只有AA-模式允许一系列中性稳定曲线,这种非震荡条件下的不稳定模式又被称为ST-模式.ST-模式导致所谓的交换稳定性机理.从图4可知,随着各向异性表面张力系数增大,稳定临界值ε∗随之减小.这就意味着,各向异性表面张力减小稳定性区域,使得交换稳定性机理更加稳定.当各向异性表面张力退化为各向同性表面张力时,即当γ4α=0,γ4β=0时,图4(a)中虚线与Xu等[12]给出的图5(a)中黑色实线一致,图4(b)中实线与Xu等[12]给出的图5(b)中红色实线一致.对比图4(a)中三条曲线,各向异性表面张力对片层共晶稳定性有显著的影响. 2)全局震荡模式 给定生长条件,令量子化条件(59)式、(64)式、(69)式和(74)式中Re(σ0)=0,Im(σ0)= ω∗=0,用数值的方法计算AA-,AS-,SA-和SS-模式对应的稳定临界值εaa∗, εas∗, εsa∗ 和εss∗. 这四种振荡不稳定模式导致了所谓的全局不稳定性机理,图5—图8给出了四种震荡不稳定模式的稳定临界值εaa∗, εas∗, εsa∗ 和εss∗ 随着υ 的变化图. 从图5、图7和图8可以看出,随着各向异性表面张力系数增大,稳定临界值εaa∗,εsa∗ 和εss∗ 随之减小. 这就意味着各向异性表面张力减小片层共晶生长的稳定性区域,增强了AA-,SA-和SS-这三种全局震荡模式的全局不稳定性;然而,对于AS-全局震荡模式而言,从图6可以看出,随着各向异性表面张力系数增大,稳定临界值εas∗随之增大.这就意味着,各向异性表面张力增大片层共晶生长的稳定性区域,减弱了AS-全局震荡模式的全局不稳定性. 图4 当σ0=0(n=0)时,对于AA-模式,临界值ε∗随υ的变化,其中ˆC∞=−0.12,w0=0.63,ϖ=0.15,ˆκ=1.33,(R c=¯Γβ/¯Γα),Mα=0.107,Mβ=−0.0711,θ+=65.3◦,θ−=59.5◦,ψ=0,ˆβ=4.88×10−10(a)临界值ε∗随υ的变化;(b)参数β∗随υ的变化Fig.4.The variation ofε∗withυfor the AA-mode when the eigenvalueσ0=0(n=0),whereˆC∞=−0.12,w0=0.63,ϖ=0.15,ˆκ=1.33,(R c=¯Γβ/¯Γα),Mα=0.107,Mβ=−0.0711,θ+=65.3◦,θ−=59.5◦,ˆβ=4.88×10−10:(a)The variation of the stability critical numberε∗ with υ;(b)the variation ofβ∗ with υ. 图5 当Re(σ0)=0,Im(σ0)= ωaa∗时,对于AA-模式,(a)临界值εaa∗随υ的变化,(b)特征频率值ωaa∗随υ的变化,其他参数取值同图4Fig.5.The variation of εaa∗ with υ for the AA-mode when the eigenvalue Re(σ0)=0,Im(σ0)= ωaa∗:(a)The variation of the stability critical number εaa∗ with υ;(b)the variation of the corresponding eigenfrequency ωaa∗withυ.The values of other parameters are the same as those given in Fig.4. 图6 当Re(σ0)=0,Im(σ0)=ωas∗时,对于AS-模式,(a)临界值εas∗随υ的变化,(b)特征频率值ωas∗随υ的变化,其他参数取值同图4Fig.6.The variation of εas∗ with υ for the AS-mode when the eigenvalue Re(σ0)=0,Im(σ0)= ωas∗:(a)The variation of the stability critical number εas∗ with υ;(b)the variation of the corresponding eigenfrequency ωas∗withυ.The values of other parameters are the same as those given in Fig.4. 图7 当Re(σ0)=0,Im(σ0)=ωsa∗时,对于SA-模式,(a)临界值εsa∗随υ的变化,(b)特征频率值ωsa∗随υ的变化,其他参数取值同图4Fig.7.The variation of εsa∗ with υ for the SA-mode when the eigenvalue Re(σ0)=0,Im(σ0)= ωsa∗:(a)The variation of the stability critical number εsa∗ with υ;(b)the variation of the corresponding eigenfrequency ωsa∗withυ.The values of other parameters are the same as those given in Fig.4. 图8 当Re(σ0)=0,Im(σ0)=ωss∗时,对于SS-模式,(a)临界值εss∗随υ的变化,(b)特征频率值ωss∗随υ的变化,其他参数取值同图4Fig.8.The variation of εss∗ with υ for the SS-mode when the eigenvalue Re(σ0)=0,Im(σ0)= ωss∗:(a)The variation of the stability critical number εss∗ with υ;(b)the variation of the corresponding eigenfrequency ωss∗withυ.The values of other parameters are the same as those given in Fig.4. 本文研究了定向凝固过程中各向异性表面张力对共晶生长形态稳定性的影响.应用多重变量渐近展开法解决了表面张力为各向异性时线性绕动态的特征值问题,导出了受各向异性表面张力影响的界面形态表达式和扰动振幅变化率与波数满足的色散关系,以此为基础给出了共晶生长的临界稳定性判据和界面形态满足的量子化条件.结果表明:各向异性表面张力对定向凝固系统的稳定性有显著的影响.与各向同性表面张力条件下的共晶凝固系统相比较,考虑各向异性表面张力的定向凝固系统中共晶生长界面形态也有两种整体不稳定机理:由非震荡导致的“交换稳定性”和由震荡导致的“整体波动不稳定性”机理.稳定性分析表明共晶界面稳定性取决于Peclet数的某一个临界值ε∗,当Peclet数大于临界值ε∗时,共晶界面形态不稳定;当Peclet数小于临界值ε∗时,共晶界面形态稳定.随着各向异性表面张力增大,对应于AA-,SA-和SS-模式的临界值εaa∗,εas∗,εsa∗ 和εss∗减小,各向异性表面张力减小稳定性区域,各向异性表面张力加强这三种模式的稳定性;然而,随着各向异性表面张力增大,对应于AS-模式的临界值εas∗也增大,各向异性表面张力增大稳定性区域,各向异性表面张力减弱AS-模式的稳定性. 本文得到了加拿大麦吉尔大学徐鉴君教授的指导与帮助,作者表示感谢.作者徐小花感谢天津城建大学陈永强教授的有益讨论与帮助. [1]Jackson K A,Hunt J D 1966 Trans.Metall.Soc.AIME 236 1129 [2]Trivedi R,Mangnin P,Kurz W 1987 Acta Metall.35 971 [3]Liu J M,Zhou Y H,Shang B L 1990 Acta Metall.Mater.38 1625 [4]Kassner K,Misbah C 1991 Phys.Rev.A 44 6533 [5]Li X,Ren Z M,Fautrelle Y,Zhang Y D,Esling C 2010 Acta Mater.58 1403 [6]Meng G H,Lin X,Huang W D 2007 J.Mater.Sci.Technol.23 851 [7]Karma A,Sarkissian A 1996 Metall.Mater.Trans.A 27 635 [8]Parisi A,Plapp M 2008 Acta Mater.56 1348 [9]Ginibre M,Akamatsu S,Faivre G 1997 Phys.Rev.E 56 780 [10]Datye V,Langer J S 1981 Phys.Rev.B 24 4155 [11]Xu J J,Li X M,Chen Y Q 2014 J.Cryst.Growth 401 93 [12]Xu J J,Chen Y Q,Li X M 2014 J.Cryst.Growth 401 99 [13]Xu J J 2017 Interfacial Wave Theory of Pattern Formation in Solidifi cation: Dendrites,Fingers,Cells and Free Boundaries(2nd Ed.)(New York:Springer)pp503–572 [14]Xu J J 2006 Introduction to kinetics of solidifi cation and stability theory of the interface(Beijing:Science Press)pp33–44(in Chinese)[徐鉴君 2006凝固过程动力学与交界面稳定性理论导引(北京:科学出版社)第33—44页] [15]Wang Z J,Wang J C,Yang G C 2008 Acta Phys.Sin.57 1246(in Chinese)[王志军,王锦程,杨根仓 2008物理学报57 1246] [16]Wang Z J,Wang J C,Yang G C 2010 Chin.Phys.B 19 017305 [17]Chen M W,Wang Z D,Xu J J 2014 J.Cryst.Growth 385 115 [18]Xu J J 1991 Physica D 51 579 [19]Chen M W,Chen Y C,Zhang W L,Liu X M,Wang Z D 2014 Acta Phys.Sin.63 038101(in Chinese)[陈明文,陈奕臣,张文龙,刘秀敏,王自东2014物理学报63 038101] [20]Seetharaman V,Trivedi R 1988 Metall.Trans.A 19 2955 [21]Mergy J,Faivre G,Guthmann C,Mellet R 1993 J.Cryst.Growth 134 353 [22]Mullins W W,Sekerka R F 1964 J.Appl.Phys.35 444 [23]Xu J J 2002 J.Cryst.Growth 245 134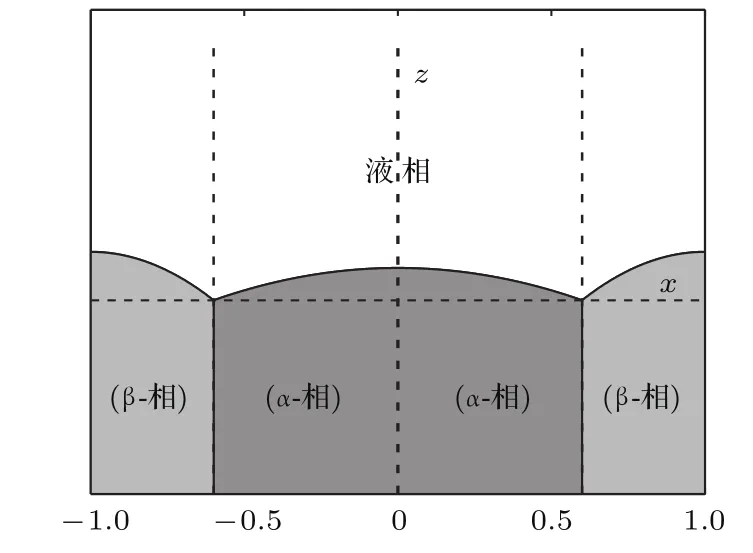
2 定向凝固系统的数学模型

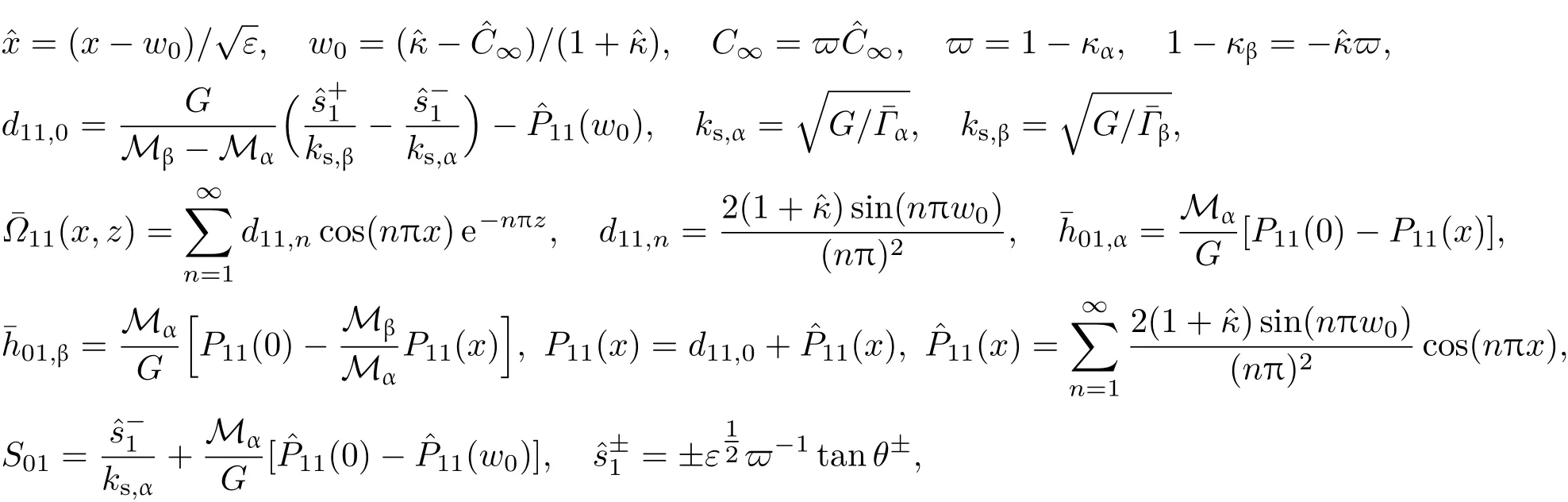
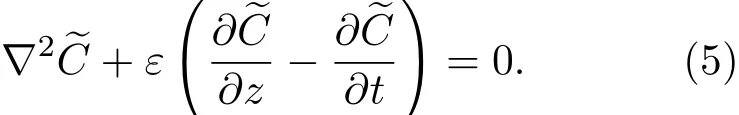

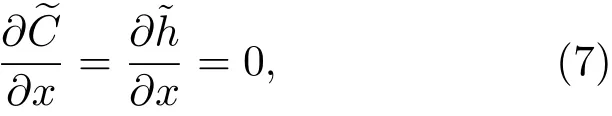

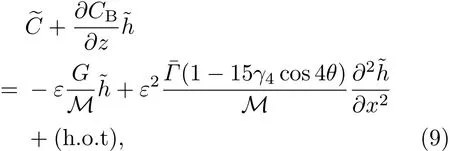

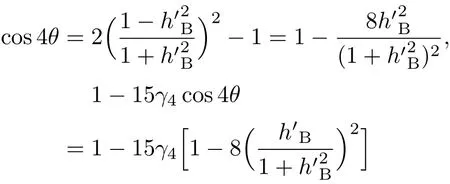
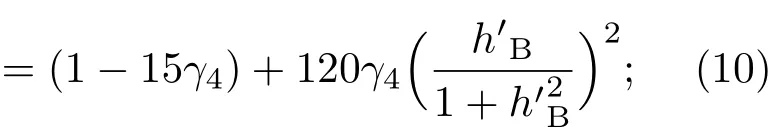
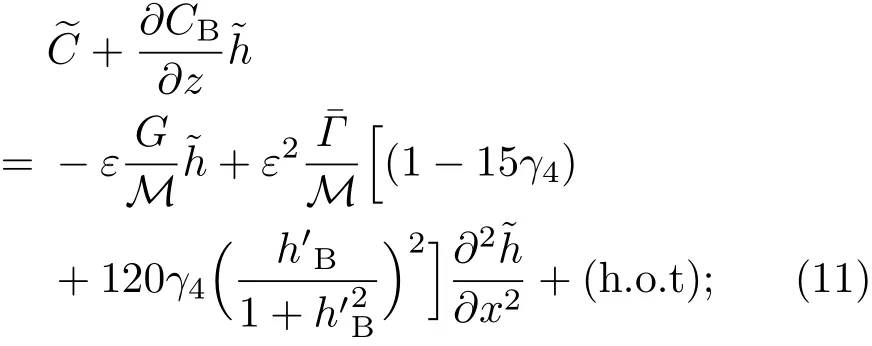
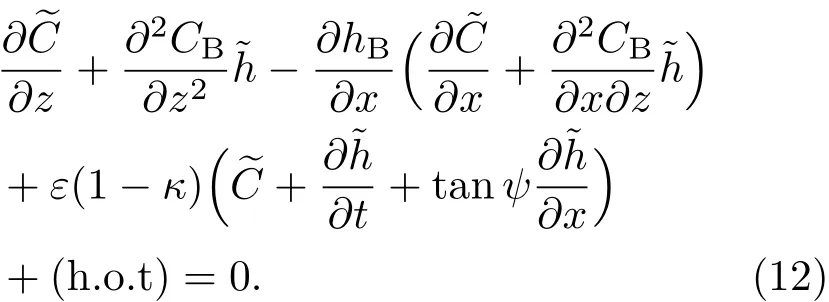
3 扰动态的多重变量渐近展开解
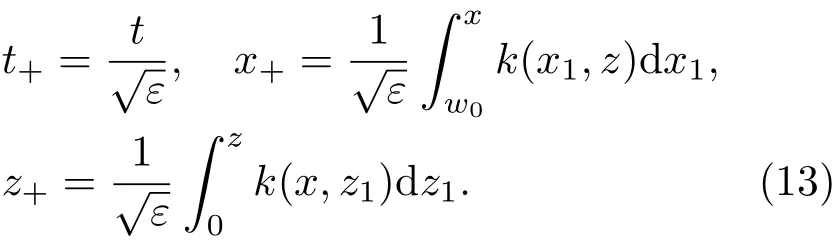
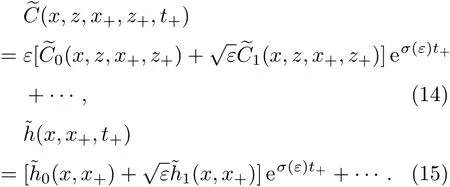
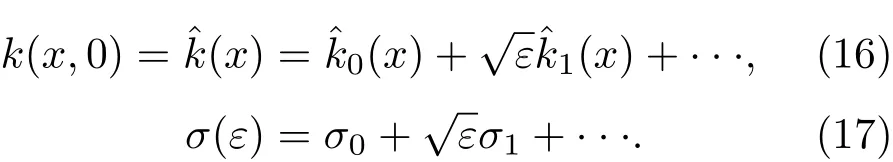
3.1 零级近似解
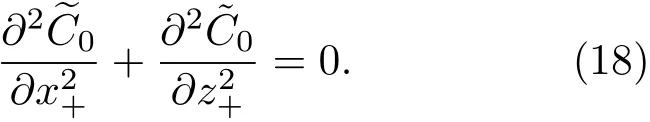

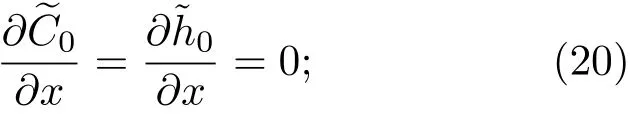

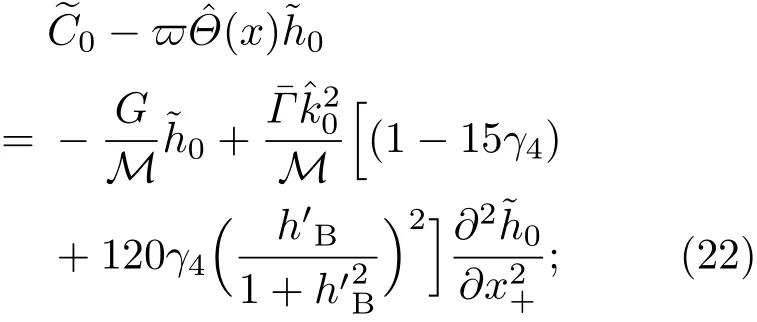
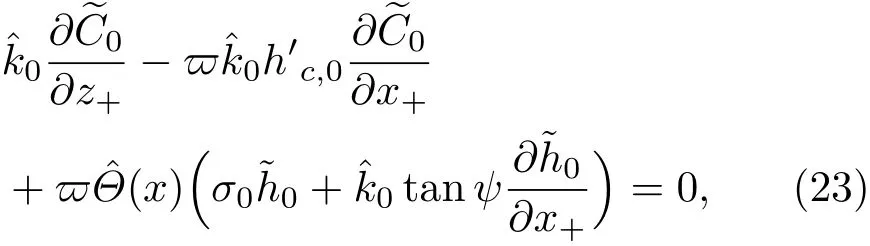
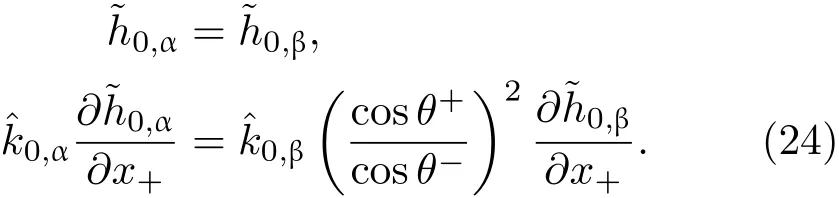
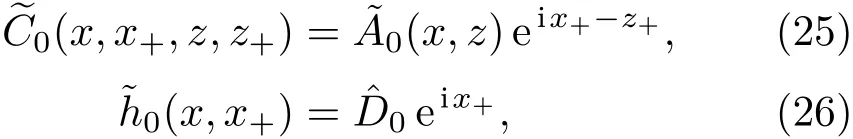
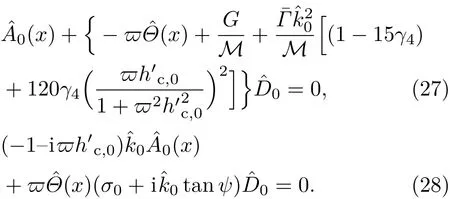

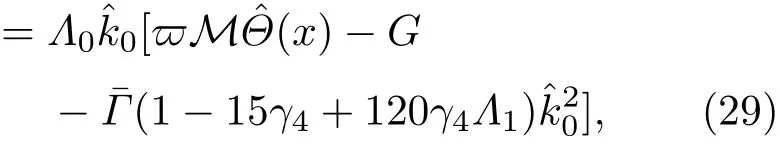
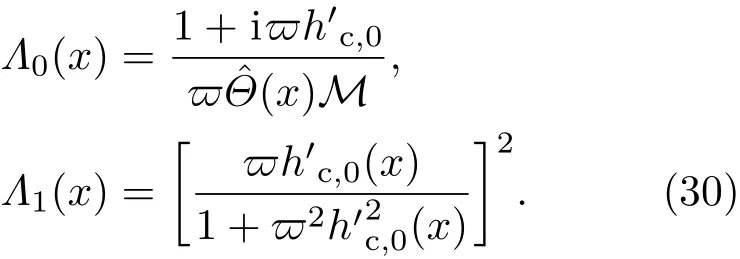
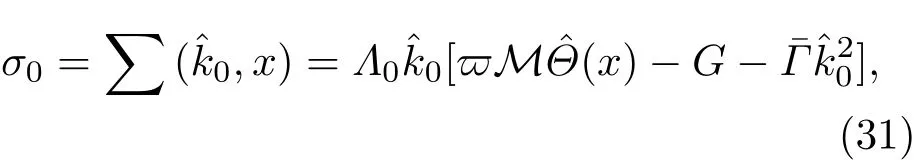
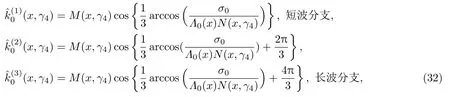
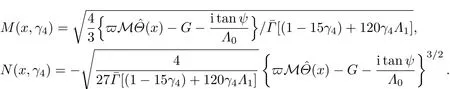
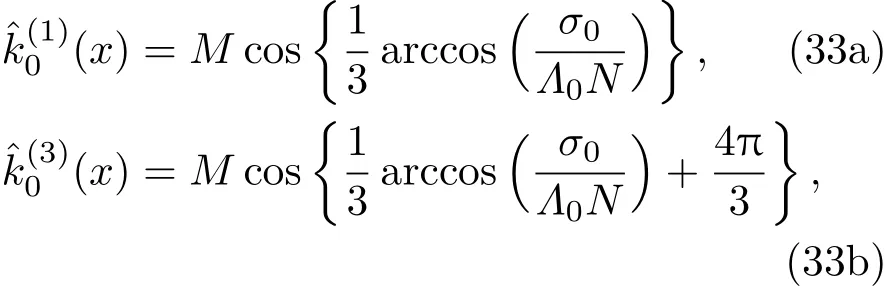
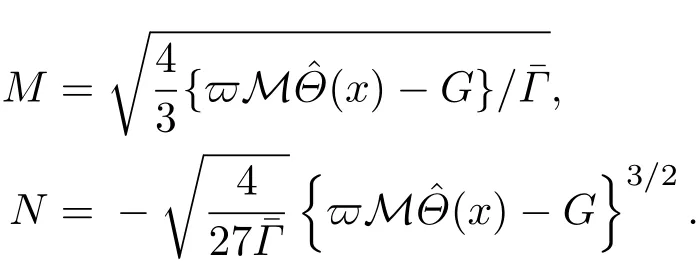
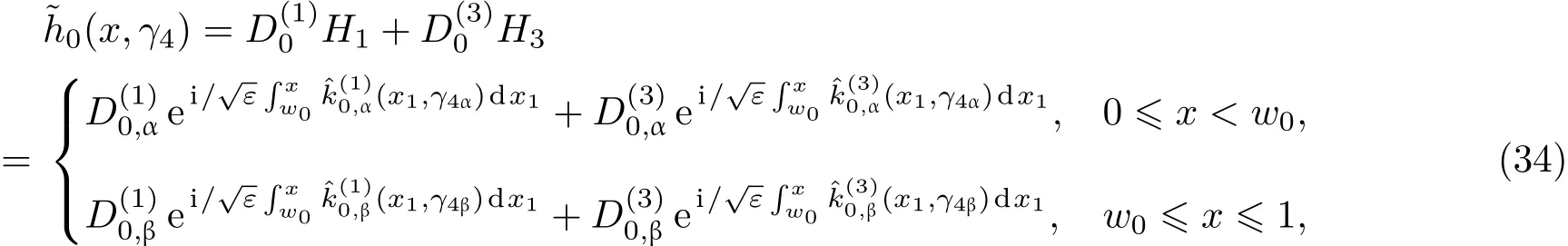
3.2 一级近似解
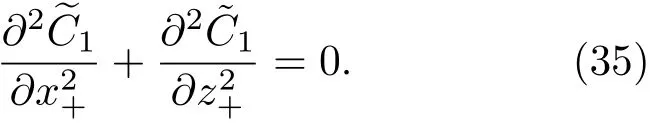



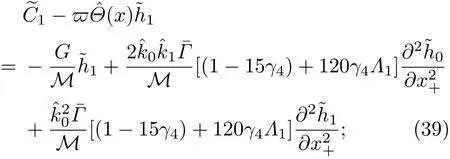
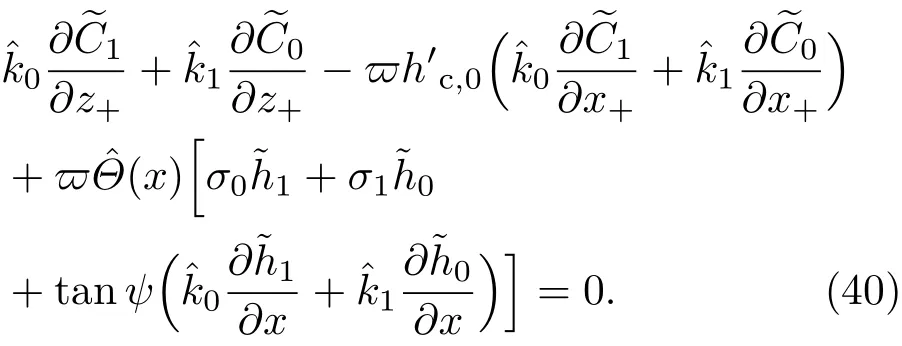
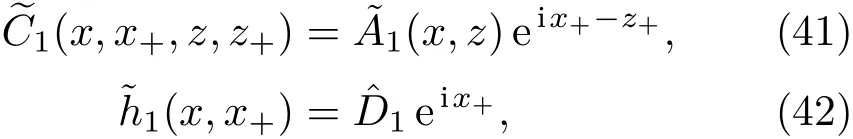

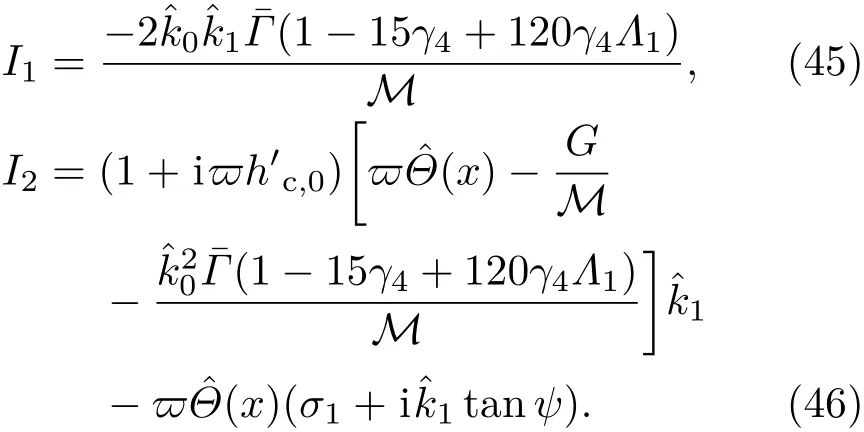
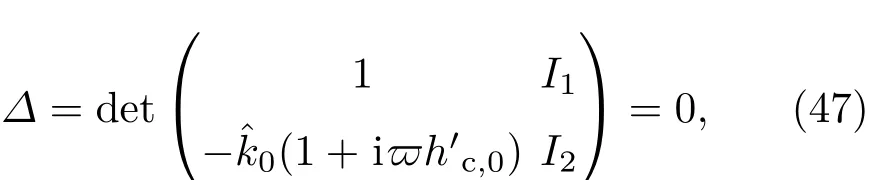
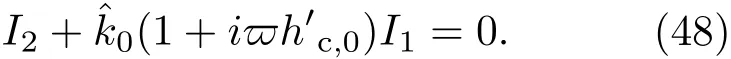
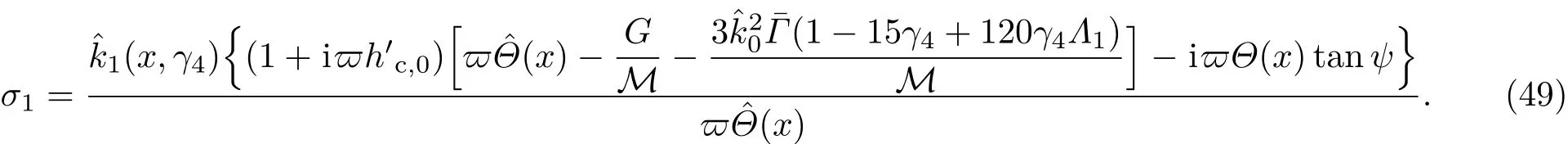
4 全局模式解和量子化条件
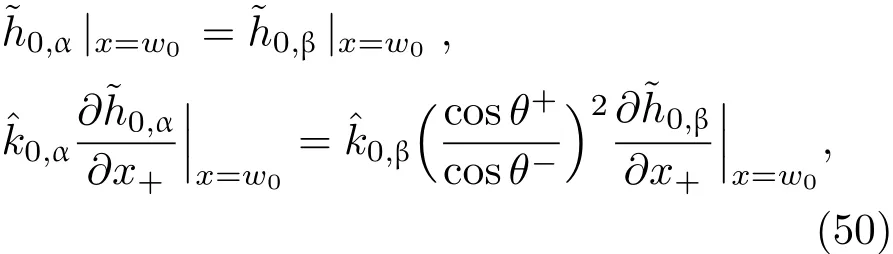
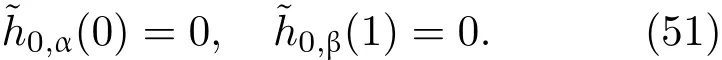
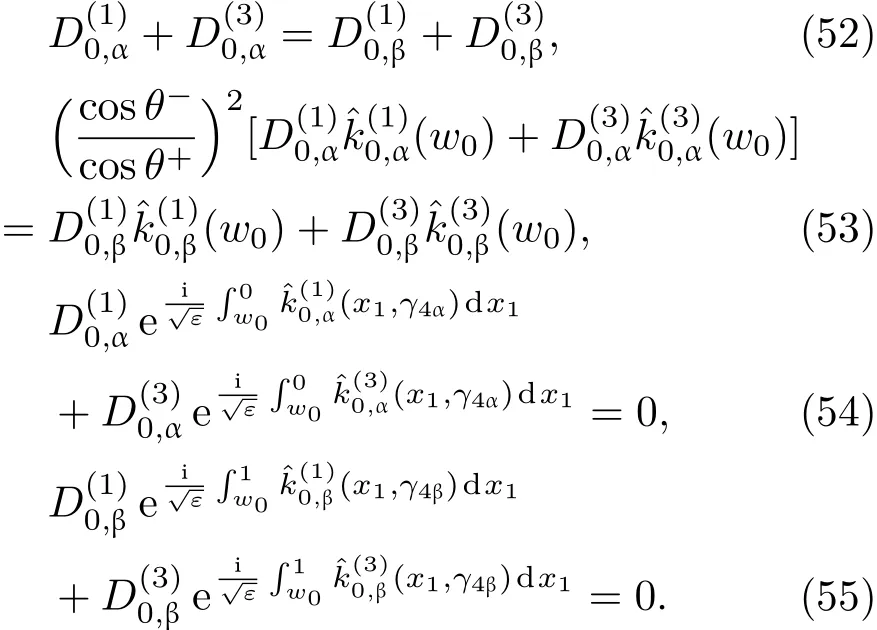
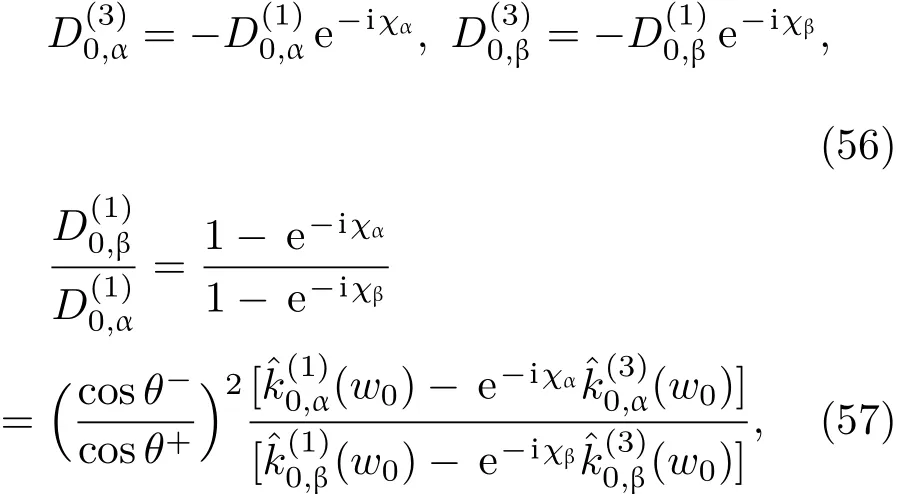
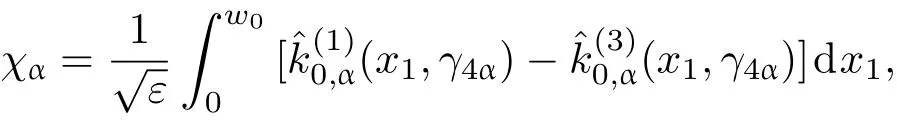
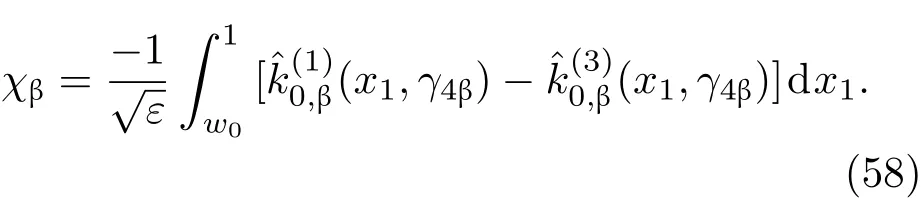
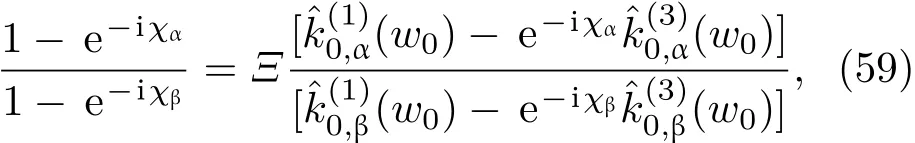
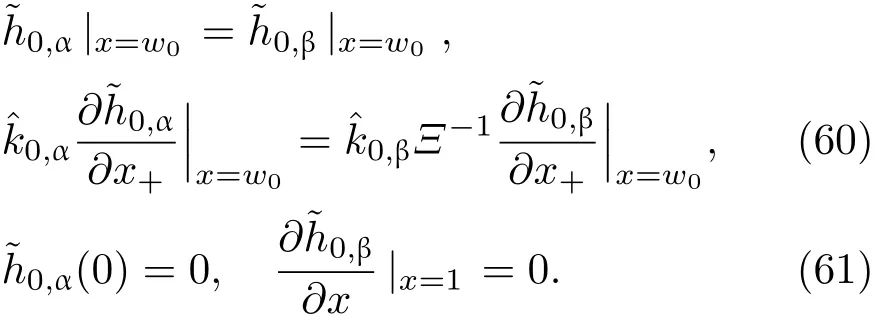
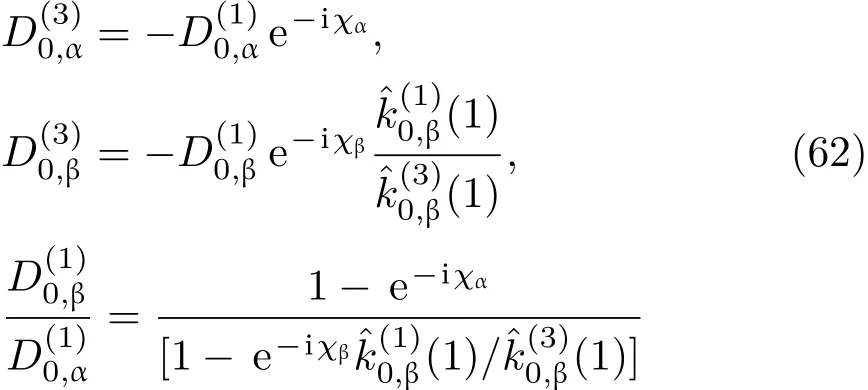

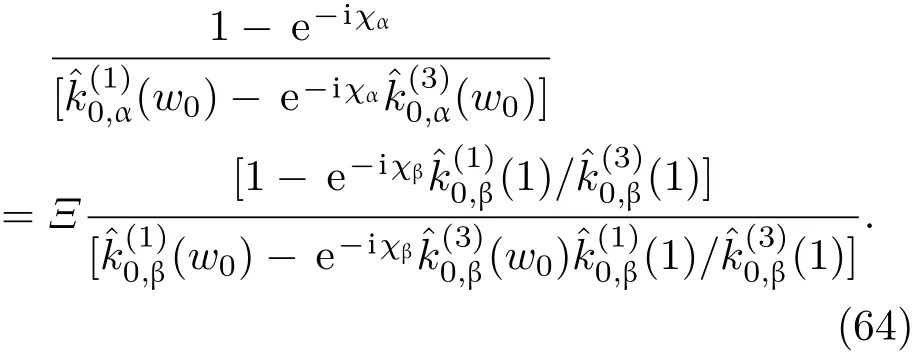
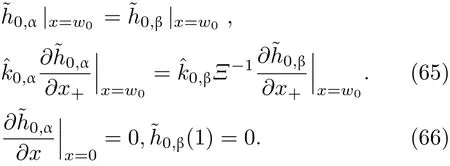
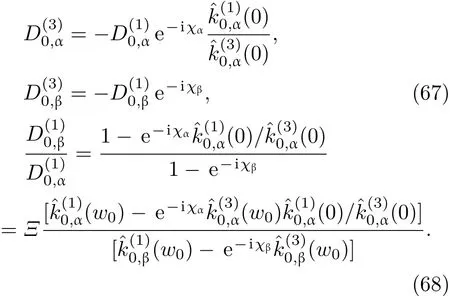
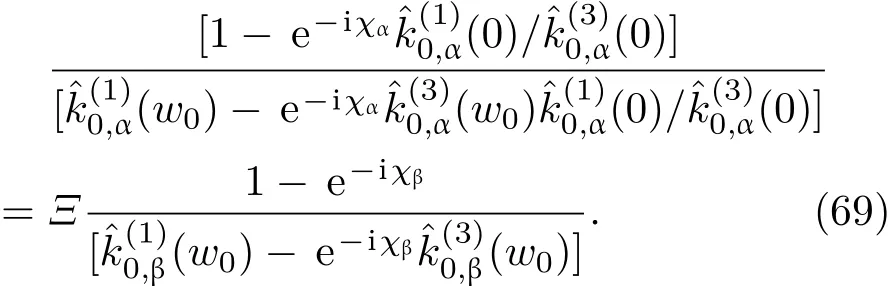
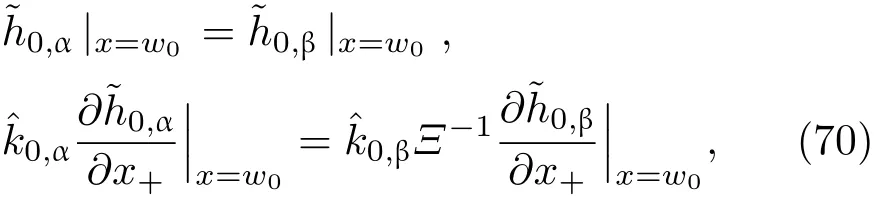
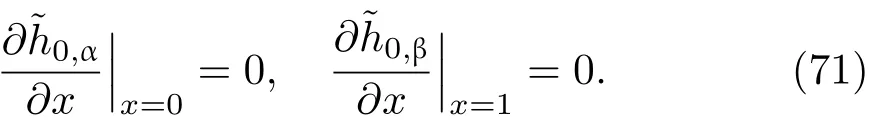
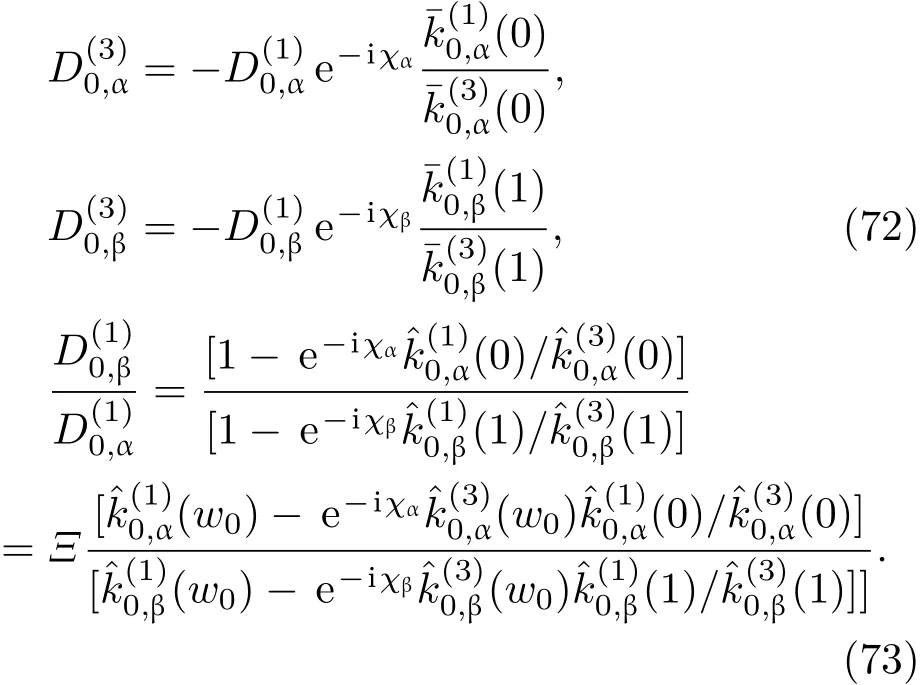
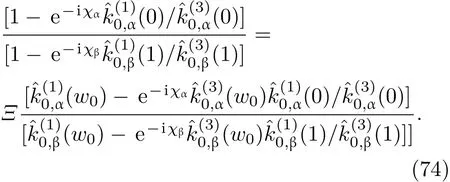
5 稳定性分析
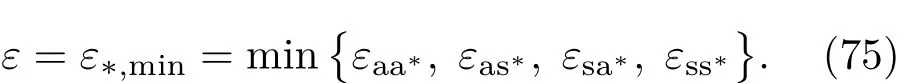
6 结 论
