基于石墨烯编码超构材料的太赫兹波束多功能动态调控∗

闫昕 梁兰菊† 张璋 杨茂生 韦德泉 王猛李院平 吕依颖 张兴坊 丁欣 姚建铨

1 引 言

太赫兹波(Terahertz,THz)是指频率为0.1—10 THz范围内的电磁辐射,处于电子学到光子学的过渡区域,也是宏观经典理论向微观量子理论的过渡区域[1].THz波特殊的频谱位置决定了其波段具有瞬态性、带宽宽、频率高、低能量、高透射等独特特性,将在宽带通信、军事雷达、生物医学、安检等领域显现出广阔的应用前景[2−6].但是随着THz应用的需求,THz波发展在某些技术方面还存在一些不足,除了THz辐射源功率能量、探测器的灵敏度以及频谱窄等问题之外,THz波的调控也是影响其应用的瓶颈之一[7−8].

电磁超构材料是一种由亚波长单元结构周期或非周期排布在二维平面上形成的平面型人工复合电磁材料,可以通过等效电阻抗、磁阻抗以及突变相位来实现对电磁波灵活多样的调控,得到国际学术界和工业界的高度关注[9−14].但是目前利用电磁超构材料调控THz波的研究仍面临许多挑战,如难以实现实时动态调控、结构复杂、可调范围小.近年来研究表明,利用石墨烯相结合的超构材料为动态调控THz波束提供了新的发展机遇,已成为THz领域新的研究热点[15−19].

石墨烯新型材料具有带隙可调、响应速度快、材料损耗小等特性,结合超构材料为动态调控波束的发展带来了新的机遇[20].2013年,瑞士洛桑联邦理工学院Carrasco等[21]设计了基于石墨烯薄膜的可调超构材料,通过改变石墨烯的费米能级可实现300◦移相,进而对THz波束进行调控.2016年,南京大学冯一军教授课题组设计了能灵活操控THz波的可切换1/4波片,实现了透射电磁波极化特性的动态切换[22].同年,Orazbayev等[23]利用多层石墨烯介电超构材料实现了一定角度范围内透射波束方向的可调.同年,西北工业大学赵晓鹏教授课题组[24]在金属膜的两面设计不同形状石墨烯超构材料产生2π移相,实现了THz波段频率偏移和分束功能.这些研究结果使得基于石墨烯超构材料对THz波束动态调控的研究越来越引起人们的关注,但目前仍面临调制单一、频带窄、幅度小等问题.

2014年,Della和Engheta[25]提出了由不同电磁特性的材料粒子构成的“数字超构材料bit位”,进而通过空间混合“数字超构材料bit位”构建“超构材料字节”,然而,这些超构材料仍然是用等效媒质参数来描述.同年,东南大学崔铁军教授课题组[26]在相位突变调控的基础上提出相位编码超构材料,并且设计制作了一款1 bit数字超构材料,通过偏置二极管实现“0”或“1”编码单元,能够在FPGA的实时控制下实现不同的编码超构材料序列,进而可构造数字编程超构材料实现多种调控功能.2016年,刘硕等[27]利用不同频率之间的正交性,设计了一款双频双功能的1 bit编码超构材料,并实验验证了其对不同频率THz的独立调控.同年,Liu等[28]将数字信号处理中的卷积运算引入到编码超表面的设计中.2017年,Cui[29]介绍了微波波段从被动超构材料到数字超构材料,最后到可编程超构材料调控电磁波所取得的进展,结果表明编码超构材料能够实时调控电磁波,并且不同序列的编码能够实现不同的调控功能.同年,Zhang[30]在编码超构材料的基础上,重点介绍了信息超构材料和超表面以及未来发展趋势.Liu和Cui[31]综述了近年来在编码和可编程超材料方面的发展,重点介绍了编码和可编程超材料的基本概念、工作原理、设计方法、制作方法和实验验证.编码超构材料具有宽频段、设计简单、灵活调控波束等优势[32−34],外加二极管使得该结构在微波波段实现波束的多功能动态调控.这种编码超构材料不需要宏观的媒质参数描述其电磁特性,只需要调控编码单元的序列就可以调控电磁波.然而由于材料性质和加工能力的限制,在传统微波波段所使用的成熟理论及技术并不能被简单地移植到THz波段进行直接运用.

本文基于石墨烯的可调电导率特性,设计了一种THz波段动态可控的1 bit编码超构材料.仿真和计算结果表明,利用不同电压调控不同列的bit单元能够动态调控编码序列,实现1.7—2.2 THz宽频段范围内波束数目以及宽度等参数的调控.对于010101周期序列,“0”和“1”单元施加不同的电压,可实现双波束频率的偏移.分析结果还表明,对于00000周期序列,在不同列施加不同的电压,可以实现特定频率下波束幅度的变化.因此本文设计的石墨烯编码超构材料能够灵活多功能动态调控THz波,将在雷达隐身、成像、宽带通信等方面具有重要的意义.

2 基于石墨烯编码超构材料动态调控THz波束的机理

2.1 THz波段石墨烯材料的特性

单层石墨烯可以用一个无限薄且具有复数电导率σs(ω,µc,Γ,T)的电导层模型来进行表征,其中ω为角频率,µc为石墨烯化学势,Γ为散射率,由电子弛豫时间τ决定 (2Γ=～/τ),T是环境温度.根据Kubo公式,其表面电导率模型可表示为复数形式:

即石墨烯的电导率由带内σintra和带间σinter组成.在THz波段,石墨烯的电导率带间部分相对于带内部分可忽略不计,所以其电导率可用类似Drude模型即(2)式来描述[35]:

其中EF为费米能级,由电掺杂或化学掺杂决定;常温情况下µc与费米能级EF近似相等;e,～和kB分别为电子电荷、普朗克常数和玻尔兹曼常数;本文取τ=0.33 ps,T=300 K.石墨烯的相对介电常数可表示为其中ε0为真空中介电常数,∆为石墨烯的厚度.

由(1)和(2)式可知,其石墨烯的电导率可由化学势控制,而化学势又可通过加载偏置电压调节.由(3)式得到石墨烯的介电常数随着电导率的变化而变化,这就为实现电导率或者介电常数可调的石墨烯提供一个有效途径.

2.2 编码超构材料调控电磁波的机理

编码超构材料调控电磁波的机理是借助反射阵天线的基本原理[26].图1为编码超构材料结构的示意图,由N×N个大小相等边长均为D的栅格构成.每个栅格是由“0”或“1”编码单元构成.第(m,n)个单元的散射相位设为φ(m,n),其取值为0◦或180◦.

图1 编码超构材料结构示意图,包含N×N个边长为D的栅格,每个栅格为“0”或者“1”编码单元组成Fig.1.The diagram of the coding metamaterial,which contains N×N lattices with dimension D,in which each lattices is occupied by “0” or “1” elements.

在垂直平面波的照射下,编码超构材料表面散射的远场函数可表示为

其中θ和φ为入射角和方位角,fe(θ,φ)为单个栅格远场的辐射函数.方向图函数表示为

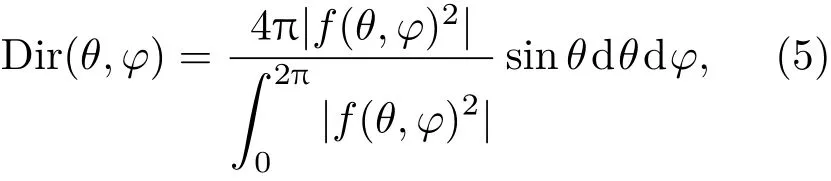
因为 “0”和“1”编码单元相位为0◦或者180◦,两单元的散射特性相消,fe(θ,φ)的辐射特性基本为0.从(4)和(5)式看出,控制电磁编码超构材料远场散射特性主要通过编码栅格单元的不同序列方式实现.

2.3 基于石墨烯带的THz编码超构材料

本文设计的编码超构材料结构如图2所示,该结构从下到上依次为金属薄膜、聚酰亚胺、硅、二氧化硅、石墨烯带组成.金的厚度为200 nm,介质层聚酰亚胺(ε1=3.1,tanδ=0.05)的厚度为h1=21 µm,硅 (ε2=11.9,σ =2.5×10−4S/m)的厚度为h2=0.7µm,二氧化硅(εr=3.75,tanδ=0.004)的厚度为h3=0.3µm.单元结构的周期Px=Py=60µm,石墨烯的宽度为w=40µm,长度为Py=60µm.若在由石墨烯带与硅构成的电极结构上施加直流偏置电压,石墨烯的化学势也将随之变化,相应地对石墨烯表面电导率进行动态控制.费米能级EF和偏压Vg之间存在如下关系式[36]:

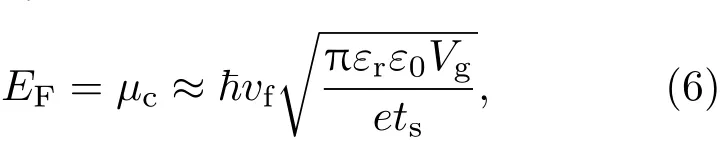
其中εr与ε0分别为二氧化硅的相对介电常数与真空介电常数,Vg表示偏置电压,ts为二氧化硅绝缘层厚度,vf表示费米速度(石墨烯为1.1×106m/s).石墨烯的费米能级一般可以在较大范围内进行调节 (0—1 eV).

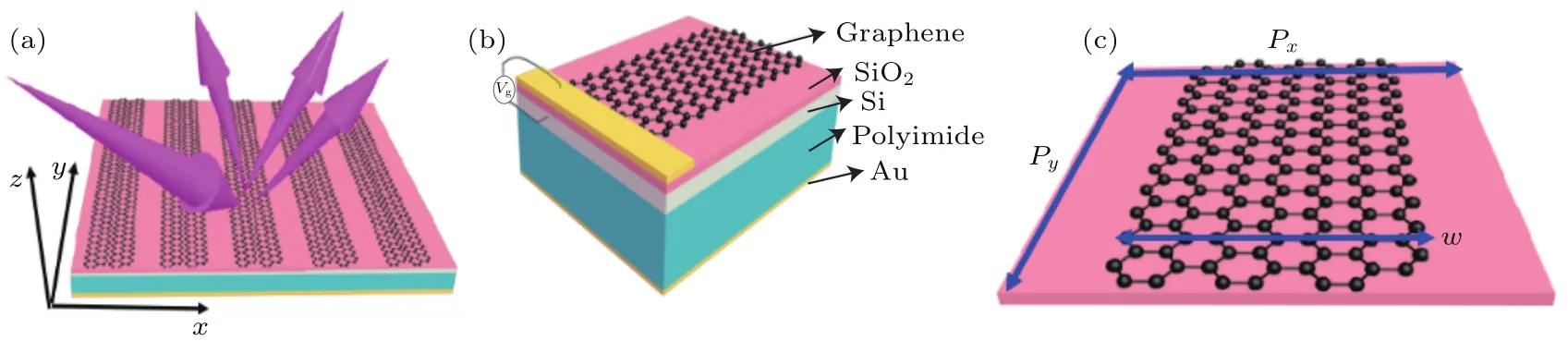
图2 设计的编码超构材料结构 (a)基于石墨烯带的编码超构材料示意图;(b)基于石墨烯带的超构材料单元结构意图;(c)超构材料的单元结构,参数设置为P x=P y=60µm,w=40µm.Fig.2.The designed metamaterial:(a)Schematic of graphene coding metamaterial;(b)unit structure of graphene metamaterial;(c)designed metamaterial with geometrical parameters P x=P y=60µm,w=40 µm.

为了进一步分析石墨烯编码超构材料动态调控THz波束的机理,利用CST microwave studio进行超构材料的全波数值仿真.在CST仿真中,假设石墨烯的厚度为1 nm,其相对介电参数可由(3)式计算并导入.在数值计算中,激励源采用平面波的形式,对图2(b)的结构进行周期单元仿真,边界条件设置为unitecell,端口设置为Floquet端口,入射波沿着z轴的负方向传播,电场沿着x轴方向,所有的网格都设置成自适应加密.

图3分析了不同频率、不同的石墨烯费米能级EF条件下石墨烯超构材料的反射相位、反射率的特性.从图3(a)看出,在1 THz与2 THz附近,通过改变EF,其超构材料的反射相位相应改变,能够从−150◦变化到150◦, 变化最大值为300◦. 因此当选择不同的石墨烯费米能级EF时,不同列的石墨烯超构结构能够产生某个频段的相位差达到180◦,这为设计编码超构材料提供了可行性.另外从图3(b)看出,在频率1 THz和2 THz附近,通过改变EF其反射率相应会发生改变,特别是在频率1 THz附近,反射率变化较大,能够从1变化到0.本文主要设计反射式的编码超构材料,反射系数不能太低.为此,本文主要研究2 THz附近的编码超构材料特性.为了进一步表征石墨烯材料特性,给出了频率2 THz处石墨烯的介电常数随费米能级变化的曲线,如图4所示.从图4看出,随着石墨烯的费米能级从0 eV增加到1.0 eV,介电常数的实部从−2688降低到−79115,介电常数的虚部从709增加到19156,石墨烯的金属性不断增强,这为设计编码超构材料以及可调特性提供了有利因素.

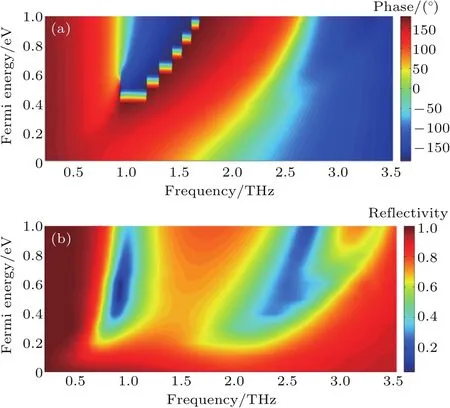
图3 不同频率、不同E F条件下其石墨烯超构材料的反射相位和反射率 (a)反射相位变化;(b)反射率变化Fig.3.Refl ected phase and refl ectivity of coding metamaterial as a function of graphene E F and THz frequency:(a)Refl ected phase;(b)refl ectivity.

图5 计算了EF=1.0 eV与EF=0.0 eV条件下,不同列的石墨烯超构材料的反射相位及相位差.从图4(b)看出,在1.75—2.6 THz带宽范围内,其EF=1.0 eV与EF=0 eV的两种情况对应的反射相位差为180◦±30◦,并且由图3(b)和图5(d)还可以得到1.75—2.2 THz频率范围内反射率相差不大,频率2.0 THz处反射相位差正好为180◦.因此可把EF=0 eV和EF=1.0 eV对应的超构材料作为编码超构材料的数字单元.另外,为了尽力消除单元与单元之间的电磁耦合,把其相邻的4个石墨烯带即子阵列共用一个偏置电压,EF=0 eV对应的超构材料定义为“0”数字编码单元,EF=1.0 eV对应的超构结构作为“1”数字编码单元,如图5(a)所示.如果选择不同列的石墨烯费米能级处于不同的EF,则其超构材料的反射相位差为180◦±30◦的带宽范围不一样,如图5(c)所示.如果费米能级为EF=1.0 eV和EF=0.2 eV两种情况,则其带宽范围为2.0—2.4 THz.如果费米能级为EF=1.0 eV和EF=0.4 eV两种情况,则其带宽范围为零.因此,这种超构材料利用对不同列的石墨烯带加载不同的电压来实现序列动态变化和频率的偏移,进一步对THz波束动态调控.

图4 频率2 THz处,石墨烯的介电常数随费米能级变化的曲线 (a)介电常数实部;(b)介电常数虚部Fig.4.The permittivity of graphene as the function of E F with 2 THz frequency:(a)Real of permittivity;(b)imaginary of permittivity.

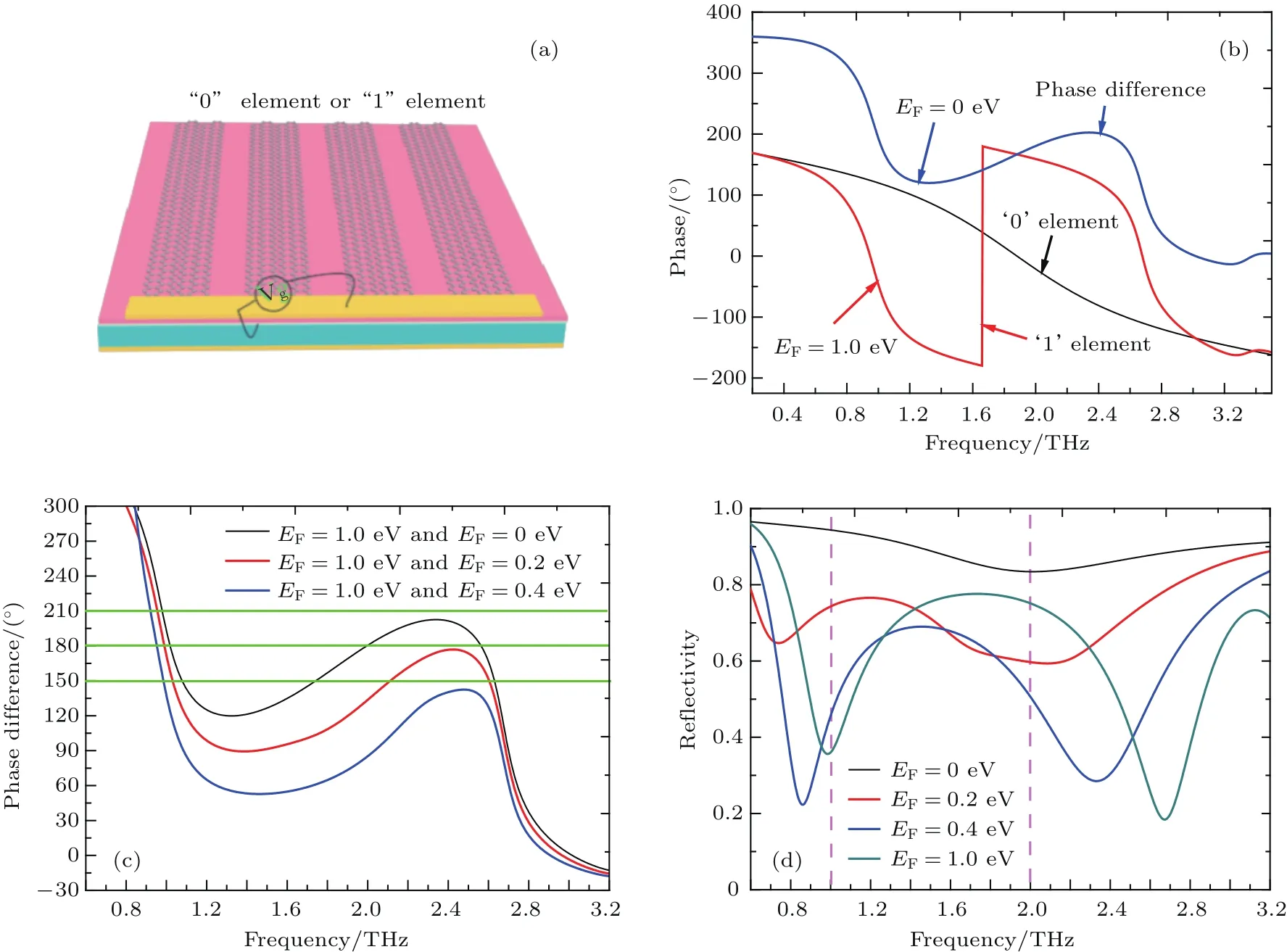
图5 石墨烯超构材料的反射相位及相位差 (a)“0”或者“1”单元编码示意图;(b)石墨烯的费米能级为E F=0 eV和E F=1.0 eV情况下,“0”或者“1”单元的反射相位;(c)三种不同石墨烯费米能级情况下,“0”或者“1”单元的反射相位差;(d)不同石墨烯费米能级情况下,超构材料的反射率Fig.5.The refl ected phase and phase diff erence of graphene metamaterial:(a)Schematic of “0” or “1” element;(b)refl ected phase of the “0” and “1” element in THz frequencies under the graphene for the E F=0 eV and E F=1.0 eV;(c)refl ected phase diff erence of the “0” and “1”element in THz frequencies under three diff erent conditions for graphene Fermi energy;(d)refl ectivity of metamaterial under the diff erence conditions graphene E F.

2.4 不同的石墨烯弛豫时间对THz编码超构材料特性的影响

前面的研究中假定了石墨烯的弛豫时间τ=0.33 ps,而不同工艺过程制备的石墨烯样品弛豫时间可能会有所不同.本文编码超构材料的特性主要与反射相位以及石墨烯处于不同的费米能级其反射相位差有很大关系.为此研究了图2(b)中结构在石墨烯费米能级为EF=0 eV和EF=1.0 eV情况下,弛豫时间τ对超构材料反射相位的影响,如图6(a)和图6(b)所示.从图中得到石墨烯的弛豫时间τ对超构材料反射相位影响不大,特别是在EF=0 eV情况下,在频率0.3—3.3 THz之间,其超构材料的反射相位基本不随弛豫时间τ的变化而变化.在EF=1 eV情况下,τ=0.1 ps与其他弛豫时间反射相位有些变化.为了进一步研究石墨烯的弛豫时间τ对编码超构材料的特性影响,计算了不同的弛豫时间τ对EF=0 eV和EF=1.0 eV之间其超构材料反射相位差的影响,如图6(c)所示.从图中看出,在τ=0.1 ps,其超构材料反射相位差为180◦±30◦的带宽范围为1.56—2.2 THz,随着弛豫时间 τ的增加,其超构材料反射相位差为180◦±30◦的带宽范围基本不变化,都基本在1.75—2.6 THz之间.在石墨烯的弛豫时间τ=0.1 ps时,仍然在较宽的范围内保持超构材料的相位差满足180◦±30◦的关系.因此,石墨烯的弛豫时间对本文设计的编码超构材料性能影响不大.

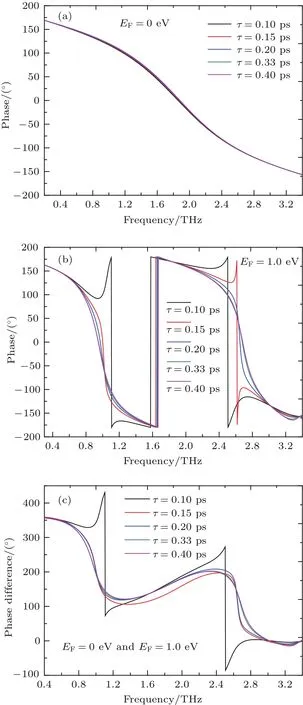
图6 (a)和(b)分别为不同的石墨烯费米能级情况,其弛豫时间τ对超构材料影响 (a)E F=0 eV;(b)E F=1.0 eV;(c)费米能级位为E F=0 eV和E F=1.0 eV之间时,τ反射相位差的变化Fig.6.The infl uence of graphene scattering timeτon the refl ected phase and phase diff erence for the THz metamaterial:(a)Refl ected phase at E F=0 eV;(b)refl ected phase at E F=1.0 eV;(c)infl uence of graphene scattering timeτon the refl ected phase diff erence for the THz metamaterial between E F=0 eV and E F=1.0 eV.

3 仿真实验分析与结果讨论

3.1 不同的编码序列对THz波束数目、形状的调控

为了研究不同的编码序列THz波束的调控特性,数值模拟研究了其不同编码序列的三维雷达散射截面(radar cross section,RCS)方向图,如图7所示.根据前面的分析,在频率2.0 THz处其对应两列石墨烯带的超构材料相位差为180◦,并且其反射率相差不大,因此主要研究此频率的散射特性.编码超构材料主要是沿x方向进行编码,y方向的编码相同,选用000000,010101,001011,001111,101111,001001 6种周期性编码序列.对于000000编码序列,每个编码所对应的散射波相位均相同,形成与入射波方向相反的反射波束,为一单波束.对于010101编码序列,将垂直入射的电磁波主要反射到两个对称的方向,形成双波束.对于001011编码序列,将垂直入射的电磁波主要分为4个方向的波束,为多波束的散射波,并且每个方向的反射能量相对应单波束而言比较低,可以用于RCS缩减.对于100111编码序列,则产生一个比较宽的扇形波束,即形成宽波束的散射波.对于001111编码序列,与010101编码序列相同,都产生一个双波束反射,但是双波束的夹角不一样.对于001001编码序列,将垂直入射的电磁波主要分为3个方向的波束.

从上述的结果看出,当超构材料的阵列单元以一定的编码序列排布时,整个超构材料将表现相应的散射波特性,改变超构材料单元的编码序列,相应的超构材料的散射特性也随之发生改变,可动态调控为不同类型的波束,包括从单波束、双波束、三波束、多波束到宽波束的散射波.

3.2 不同石墨烯费米能级对THz波束的频率动态调控特性

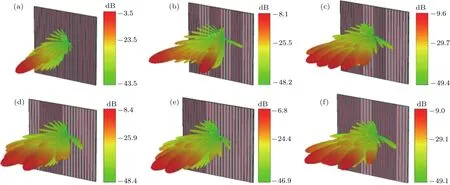
图7 在2 THz处,超构材料处于不同编码时三维RCS方向图 (a)000000;(b)010101;(c)001011;(d)100111;(e)001111;(f)001001Fig.7.3D RCS patterns for diff erent coding sequence of metamaterial under normal incidence of at 2 THz:(a)000000;(b)010101;(c)001011;(d)100111;(e)001111;(f)001001.

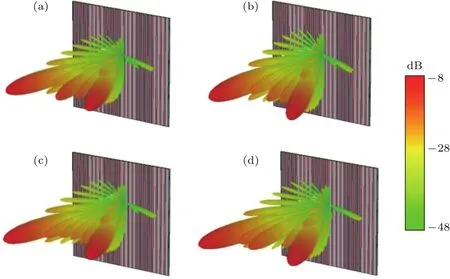
图8 对于序列010101,编码超构材料处于不同频率时三维RCS方向图 (a)1.75 THz;(b)1.9 THz;(c)2.0 THz;(d)2.2 THzFig.8.3D RCS patterns for diff erent THz frequencies of coding metamaterial under normal incidence of at 010101 sequence:(a)1.75 THz;(b)1.9 THz;(c)2.0 THz;(d)2.2 THz.

为了进一步研究太赫兹波束动态调控特性,研究了不同频率处同一编码序列处于不同频率时三维RCS方向图,如图8所示.编码超构材料“0”数字单元对应EF=0 eV情况,“1”数字单元对应EF=1.0 eV情况,其周期性编码序列010101.从图8看出,在频率为1.75,1.9,2.0和2.2 THz处,编码超表面都可将垂直入射的电磁波主要反射到两个对称的方向,形成两个主要反射瓣即双波束,不同频率处的反射波束的其他旁瓣有所不同.这是因为从图3(b)和(c)得到,在频率为1.7—2.6 THz范围内,其“0’单元与“1”单元的反射相位差为180◦± 30◦,并且在1.75—2.2 THz范围内反射率相差不大.因此,由上述分析结果得到,只要两个编码单元的反射相位差为180◦±30◦,就能实现对THz波束调控基本一致.由图4(c)分析结果还得到,若利用EF=1.0 eV与EF=0.2 eV两种条件构成的编码单元,则其结构的反射相位差为180◦±30◦,带宽范围为2.0—2.4 THz,此频率范围内同样能实现对THz波束调控基本一致.因此,对于编码序列相同的超构材料,利用加载在数字编码单元不同电压,还可以实现宽频段波束的频率的调控.

3.3 不同石墨烯费米能级对THz波束的幅度动态调控特性

为了研究石墨烯费米能级对THz波束的幅度动态调控特性,首先对超构材料的反射谱与石墨烯费米能级之间的关系进行模拟,接着对000000周期性编码超构材料处于不同石墨烯费米能级时,研究其结构的三维RCS方向图.

图9(a)为不同石墨烯的费米能级情况下图2(b)超构材料结构的反射谱.从图中可以看出,随着石墨烯费米能级的增加,出现两个谐振频率f1和f2,谐振频率处的反射率逐渐变小,谐振逐渐增强并且谐振频率逐渐蓝移,特别在2 THz附近,共振频率的改变非常显著.石墨烯的费米能级与谐振频率之间的关系如图9(d)所示,星号和圆点分别表示数值模拟的f1和f2谐振频率变化的曲线,红色线和蓝色线为相应频率变化拟合的曲线.两个谐振频率随着石墨烯的费米能级变化基本呈线性关系,分别为f1=0.6857+0.329EF和f2=1.882+0.868EF.当EF=0.1 eV时,f1=0.69 THz和f2=1.88 THz;当EF=1.0 eV时,f1=0.99 THz和f2=2.70 THz,频率偏移量分别为0.30 THz和0.82 THz.为了分析其机理,数值模拟了EF=1.0 eV情况下,谐振频率f1=0.99 THz和f2=2.70 THz的表面电流[见图9(b),(c)]和磁场分布|Hy|[见图9(e),(f)].

从图9(b),(c),(e),(f)得到,f1的表面电流主要分布在石墨烯结构表面,f2的表面电流主要分布相邻石墨烯结构之间.f1的磁场位于石墨烯结构表面上,f2的磁场主要分布在石墨烯表面和相邻石墨烯结构之间.因此,频率f1主要是基模共振,频率f2主要来自单元石墨烯结构之间的耦合为高阶谐振,频率f2对石墨烯的电导率变化更明显.因此,随着石墨烯费米能级EF的增加,共振频率f2相比f1其改变更加明显.另外,随着石墨烯费米能级EF的增加,由类似电介质特性变成金属特性,导致谐振逐渐增强并且谐振频率发生变化.

图9 (a)石墨烯处于不同费米能级情况下,超构材料的反射谱;(b)E F=1.0 eV时,谐振频率f 1=0.99 THz的表面电流;(c)E F=1.0 eV时,谐振频率f 2=2.70 THz的表面电流;(d)石墨烯的费米能级与谐振频率之间的关系;(e)E F=1.0 eV时,谐振频率f 1=0.99 THz的磁场分布|H y|;(f)E F=1.0 eV时,谐振频率f 2=2.70 THz的磁场分布|H y|Fig.9.THz amplitude dynamic adjustment performance of graphene Fermi energy:(a)Refl ection diagram of metamaterial under thediff erence graphene E F;(b)surface current distribution at f 1=0.99 THz under E F=1.0 eV;(c)surface current distribution at f 2=2.70 THz under E F=1.0 eV;(d)resonance frequency with the diff erent graphene E F;(e)magnetic fi eld distribution|H y|at f 1=0.99 THz under E F=1.0 eV;(f)magnetic fi eld distribution at f 2=2.70 THz under E F=1.0 eV.

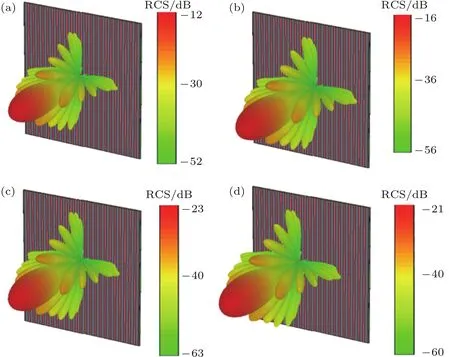
图10 对于周期性序列000000编码超构材料,在频率f 1=1 THz处,不同E F时其结构的三维RCS方向图 (a)E F=0 eV;(b)E F=0.3 eV;(c)E F=0.6 eV;(d)E F=1.0 eVFig.10.3D RCS patterns for diff erent E F of 000000 sequence coding metamaterial at f 1=1 THz:(a)E F=0 eV;(b)E F=0.3 eV;(c)E F=0.6 eV;(d)E F=1.0 eV.

图10 为周期性序列000000编码超构材料,在频率f1=1 THz处,不同石墨烯费米能级时其结构的RCS方向图.从模拟结果得到,随着石墨烯费米能级EF的变化,其RCS的最大值发生变化,当EF=0.6 eV时为最小值,这与反射率的变化曲线一致,并且其变化值从−12 dB到−23 d B,改变了11 d B.因此,通过改变石墨烯的费米能级,对于相同序列的编码超构材料,能够对反射波束的幅度进行调控.

4 结 论

本文设计的基于石墨烯带的编码超构材料,能够对THz波束进行多功能参数的动态调控.仿真结果表明,通过在不同列的石墨烯带上加不同电压,能够调控超构材料的编码序列,不同序列的编码超构材料能够实现宽频段波束数目从单波束、双波束、三波束、多波束到宽波束的调控.对于同样序列的编码超构材料,施加石墨烯带的电压不同能够实现宽频段波束频率的偏移,宽频段的范围从1.75—2.2 THz变化到2.2—2.4 THz.对于000000或者111111周期编码超构材料,施加石墨烯带的电压不同还能够实现波束幅度的调控.这种编码超构材料将在雷达隐身、成像、宽带通信等方面具有重要的意义.

[1]Tonouchi M 2007 Nat.Photon.1 97

[2]Pawar A Y,Sonawane D D,Erande K B,Derle D V 2013 Drug Invent.Today 5 157

[3]Nagatsuma T,Ducournau G,Renaud C C 2016 Nat.Photon.10 371

[4]Alves F,Grbovic D,Kearney B,Karunasiri G 2012 Opt.Lett.37 1886

[5]Benz A,Rall M,Schwarz S,Dietze D,Detz H,Andrews A M,Schrenk W 2014 Sci.Rep.4 4269

[6]Chen S,Hu W D 2017 Radio Commun.Technol.43 01(in Chinese)[陈实,胡伟东2017无线电通信技术43 01]

[7]Shen H P,Koschny T T,Soukoulis C M 2014 Phys.Rev.B 90 115437

[8]Dabidian N,Gupta S D,Kholmanov I,Lai K,Lu F,Lee J W,Jin M Z,Trendafi lov S,Khanikaev A,Fallahazad B,Tutuc E,Belkin M A,Gennady S 2016 Nano Lett.16 3607

[9]Zheludev N I 2010 Science 328 582

[10]Sun S,He Q,Xiao S,Xu Q,Li X,Zhou L 2012 Nat.Mater.11 426

[11]Han J F,Cao X Y,Gao J,Li S J,Zhang C 2016 Acta Phys.Sin.65 044201(in Chinese)[韩江枫,曹祥玉,高军,李思佳,张晨2016物理学报65 044201]

[12]Wang G D,Liu M H,Hu X W,Kong L H,Cheng L L,Chen Z Q 2014 Chin.Phys.B 23 017802

[13]Jia S L,Wan X,Su P,Zhao Y J,Cui T J 2016 AIP Advan.6 045024

[14]Zhang Y,Feng Y J,Jiang T,Cao J,Zhao J M,Zhu B 2017 Acta Phys.Sin.66 204101(in Chinese)[张银, 冯一军,姜田,曹杰,赵俊明,朱博2017物理学报66 204101]

[15]Lee S H,Choi M,Kim T T,Lee S,Liu M,Yin X B,Choi H K,Lee S S,Choi C G,Choi S Y,Zhang X,Min B 2012 Nat.Mater.11 936

[16]Shen N H,Koschny T,Soukoulis C M,Tassin P 2014 Phys.Rev.B 90 115437

[17]Dabidian N,Dutta-Gupta S,Kholmanov I,Lai K,Lu F,Jongwon L,Jin M Z,Trendafi lov S,Khanikaev A,Fallahazad B,Tutuc E,Shvets G 2016 Nano Lett.16 3607

[18]Sensale-Rodriguez B,Yan R,Kelly M M,Fang T,Tahy K,Hwang W S,Debdeep J,Liu L,Xing H G 2012 Nat.Commun.3 780

[19]Gao H,Yan F P,Tian SY,Bai Y 2017 Chinese J.Lasers 44 0703024(in Chinese)[高红,延凤平,谭思宇,白燕2017中国激光44 0703024]

[20]Sherrott M C,Hon P W C,Fountaine K T,Garcia J C,Ponti S M,Brar V W,Sweatlock L A,Atwater H A 2017 Nano Lett.17 3027

[21]Carrasco E,Tamagnone M,Perruisseau-Carrier J 2013 Appl.Phys.Lett.102 104103

[22]Zhang Y,Feng Y J,Zhu B,Zhao J M,Jiang T 2016 Opt.Express 23 27230

[23]Orazbayev B,Beruete M,Khromova I 2016 Opt.Express 24 8848

[24]Su Z X,Chen X,Yin J B,Zhao X P 2016 Opt.Lett.16 3799

[25]Della G C,Engheta N 2014 Nat.Mater.13 1115

[26]Cui T J,Qi M Q,Wan X,Zhao J,Cheng Q 2014 Light:Sci.Appl.3 e218

[27]Liu S,Zhang L,Yang Q L,Xu Q,Yang Y,Noor A,Zhang Q,Shahid I,Wan X,Tian Z,Tang W X,Cheng Q,Han J G,Zhang W L 2016 Adv.Opt.Mater.4 1965

[28]Liu S,Cui T J,Zhang L,Xu Q,Wang Q,Wan X,Gu J Q,Tang W X,Qi M Q,Han J G,Zhang W L,Zhou X Y,Cheng Q 2016 Adv.Sci.3 1600156

[29]Cui T J 2017 J.Opt.19 084004

[30]Zhang L 2017 J.Mater.Chem.C 5 3644

[31]Liu S,Cui T J 2017 Adv.Opt.Mater.5 1700624

[32]Liang L J,Qi M Q,Yang J,Shen X P,Zhai J Q,Xu W Z,Jin B B,Liu W W,Feng Y J,Zhang C H,Lu H,Chen H T,Kang L,Xu W W,Chen J,Cui T J,Wu P H,Liu S G 2015 Adv.Opt.Mater.3 1374

[33]Yan X,Liang L J,Liu W W,Ding X,Yang J,Xu D G,Zhang Y T,Cui T J,Yao J Q 2015 Opt.Express 23 29128

[34]Yan X,Liang L J,Zhang Y T,Ding X,Yao J Q 2015 Acta Phys.Sin.64 158101(in Chinese)[闫昕,梁兰菊,张雅婷,丁欣,姚建铨2015物理学报64 158101]

[35]Hanson G W 2008 J.Appl.Phys.103 064302

[36]Gómez-Díaz J S,Perruisseau-Carrier J 2013 Opt.Express 21 15490