基于自适应无参经验小波变换和选择集成分类模型的运动想象∗
2018-06-19何群王煜文杜硕陈晓玲谢平
何群 王煜文 杜硕 陈晓玲 谢平
1 引 言
随着人类对大脑了解的日益深入和科学技术的迅速发展,脑机接口(brain computer interface,BCI)技术使人们逐渐将思维活动控制现实世界的设想走向现实,该技术不依赖传统的脑神经和肌肉控制通路,而是通过直接采集大脑的神经生物电信号,构建与外部世界的直接信息传输通路[1,2].本文研究的运动想象BCI是基于自发脑活动BCI的典型代表[3].运动想象是指人们只是想象肢体做出某种动作而未实际做出动作.研究发现,运动想象时产生的脑电(electroencephalography,EEG)信号[4]具有和实际动作时EEG信号类似的事件相关同步(event-related synchronization,ERS)和事件相关去同步(event-related desynchronization,ERD)现象,当人们想象某一侧运动时,其对侧相应大脑皮层区域脑电的mu节律(8—13 Hz)和beta节律(14—30 Hz)频段幅值降低出现ERD现象,而同侧大脑EEG的mu节律和beta节律频段幅值升高出现ERS现象[5].这种感觉运动区EEG节律的差异是运动想象类BCI的重要特征和依据.
针对EEG信号非线性和非平稳性的特点[6−8],近些年涌现出了很多关于EEG信号的处理方法,如小波变换(wavelet transform,WT)[9]、希尔伯特 -黄 变 换 (Hilbert Huang transform,HHT)[10]、经验模态分解(empirical mode decomposition,EMD)[11]、总体经验模态分解(ensemble empirical mode decomposition,EEMD)[12]以及共空间模式(common spatial pattern,CSP)[13]等方法.WT方法不能同时在时域和频域有较高的分辨率;EMD方法在一定程度上克服了WT方法的不足,相比于WT,其最大的优点是无需事先设定分解层次,但EMD分解后的信号存在边界效应和模态混叠现象[14];EEMD方法有效解决了模态混叠现象,然而,该方法计算量较大;CSP以及其改进算法被广泛应用,并取得良好的效果[15],但该方法多用于多电极分布的BCI实验中.
针对EMD的不足,Gilles[16]结合EMD的自适应性和小波分析的理论框架,提出了一种新的信号处理方法,即经验小波变换(empirical wavelet transform,EWT).针对传统的EWT并不能实现频谱的完全自适应分割的问题,本文采用的自适应无参经验小波变换(adaptive parameterless empirical wavelet transform,APEWT)[17,18],可以实现频谱的完全自适应分割.APEWT方法不仅解决了EMD的模态混叠问题,且分解信号所需时间较EEMD短,故本文将APEWT方法应用于EEG信号分析中.当每个受试者在进行运动想象实验时,发生ERD/ERS现象的时段和频段不同,经验主义的判断无法有效评估每个受试者的最佳时段和频段[19].针对此问题,文献[15]根据巴式距离有效选择出了最佳频率段,本文方法根据不同时段和不同频段特征的分类效果为其分配不同的权重,相对单独考虑最佳频段更加全面.集成分类器可以得到比单个分类器更优的分类效果,能够提高学习能力和泛化特性,且较好地解决了特征选择算法所依据的准则或目标经常与分类器的目标不一致和容易产生选择的特征并不能满足分类模型最优化条件的问题[20].因此,本文提出利用APEWT和选择集成分类模型对运动想象EEG信号进行分类识别,综合考虑了运动想象EEG信号在不同时段和频段上的特征,构建了一种选择集成分类模型,实验结果证明了该方法的有效性.
2 数据采集与处理
2.1 数据采集
为了验证本文方法的有效性和普适性,实验中采用来自两组竞赛数据集的6名不同受试者(S1—S6)的左右手运动想象数据.第一组数据集包含被试S1来自2003年国际BCI大赛Dataset III,包含280个试次;第二组数据集包含被试S2—S6来自2008年国际BCI大赛Dataset 2b,每名受试者包含720个试次,两组数据的实验范式略有不同,详情请见文献[21,22].
下面主要对第一组数据集进行详细介绍,受试者是一名健康的25岁女性,所有的实验(Trails)都在都在同一天进行,实验包含7组,每组有40个Trails,总共280个Trails.每个Trail持续的时间为9 s,受试者在前2 s处于放松的状态;在t=2 s时,显示器出现“+”形图案,同时有提示音提示受试者实验开始,“+”保持1 s时间;在t=3 s时,显示器上出现向左或向右的箭头,提示受试者按箭头方向想象用手去移动屏幕上的条形棒,每个Trail数据采集到第9 s结束,运动想象脑电采集范式如图1所示.实验使用AgCl电极,数据采集来自C3,Cz和C4三个通道,EEG信号由双导联方式记录,采样频率为128 Hz,最终的实验数据由140个训练样本和140个测试样本组成.
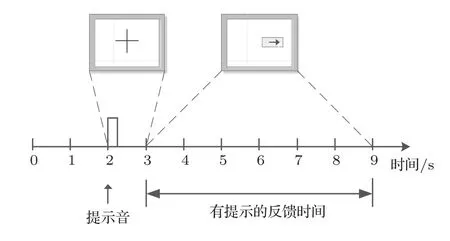
图1 运动想象脑电采集范式Fig.1.Paradigm of EEG acquisition for motor imagery.
2.2 数据预处理
为了更有效地提取EEG信号的特征,需要对数据进行简单的预处理.首先去除数据中为“NaN”的空白数据点并置为0,为了降低处理信号的复杂度,对数据集进行了重采样(250—128 Hz).由于运动想象所诱发的ERD/ERS现象主要是在mu和beta节律段,故采用8—30 Hz的六阶巴特沃斯带通滤波器对原始EEG进行滤波,其阻带截止频率为5—33 Hz,阻带衰减为50 d B,通带衰减为0.5 d B,对数据集进行统一的滤波处理,以提高信号的信噪比.
3 研究方法
首先,对原始EEG信号进行预处理.然后,使用经APEWT分解后的最优模态重构后的信号和最优模态,分别获得C3和C4通道的能量谱(energy spectrum,ES)和边际谱(marginal spectrum,MS)特征,并分别计算C3和C4通道特征的差值,通过加窗的方法得到不同时间段的ES特征和不同频段的MS特征.具体做法是:将ES特征按时间分为3段,对得到的ES特征以2 s特征为长度滑动分割3—7 s ES特征,步长为1 s特征,将每段重采样(128—4 Hz)后的ES特征作为基分类器的输入特征向量;将MS特征按频率分为10个子频带,对得到的MS特征以4 Hz特征为长度滑动分割8—30 Hz频带特征,步长为2 Hz特征,将每个子频带内的数据作为基分类器的输入特征向量,分别为每个基分类器的结果分配权重.最后,通过决策分类获得其最终的分类结果,运动想象模式识别整体流程图如图2所示.

图2 运动想象模式识别整体流程图Fig.2.Integrated fl ow chart of motor imagery pattern recognition.
3.1 自适应无参经验小波变换
EWT将信号f(t)分解成N+1个本征模态函数(intrinsic mode function,IMF)fk(t)之和,表达式为

一个IMF函数即为一个调幅-调频(amplitude modulated-frequency modulated,AM-FM)函数,IMF函数fk(t)定义为

式中Fk(t)>0, ϕ′k(t)>0, ϕ′k(t)是 ϕk(t)的导数,Fk(t)和ϕ′k(t)的变化速度比ϕk慢得多. 在EWT中,需要对Fourier谱进行自适应地分割,从而选择出合适的小波滤波器组.
在确定分割区间后,Gilles[16]根据Littlewood-Paley和Meyer小波的构造方法构造EWT.在EWT中,如何进行频谱分割是至关重要的,因为它直接关系到分解的结果.APEWT中的Fourier谱分割方法以一种自适应无参的方法自动在直方图或频谱中找到有意义的模态为目标,基于所考虑直方图的尺度空间[23]表示,以更简单的方式表达“有意义的模态”的概念,该方法的优点是简单,运行速度非常快.
原始信号f(t)的重构公式为
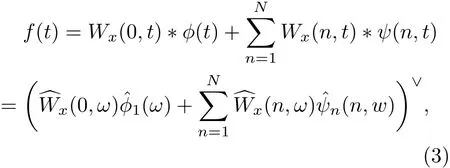
式中∗为卷积计算;Wx(n,t)为细节系数,Wx(0,t)为近似系数,ˆWx(n,t)和ˆWx(0,t)分别为Wx(n,t)和Wx(0,t)的Fourier变换;ϕ(w)为经验尺度函数,ψn(w)为经验小波函数,ˆϕ(w)和ˆψn(w)分别为ϕ(w)和ψn(w)的Fourier变换.
本征模态分量fk(t)定义如下:

3.2 最优模态选择
EEG信号经APEWT分解后,模态分量较多,但某一动作模式下的对应区域EEG信号主要集中在特定频段,因此选取能量最为集中的分量是非常必要的.本文借鉴文献[24]中方法,将APEWT分解后的各模态与原始EEG信号的相关系数作为评定各模态分量的指标,定义如下:
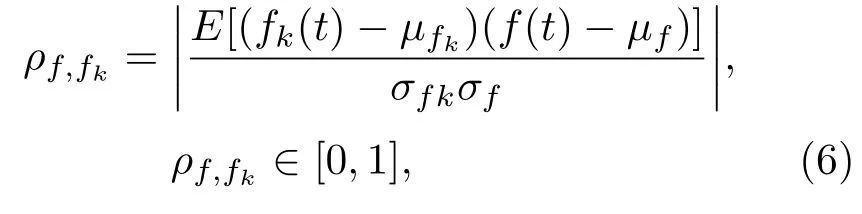
式中fk(t)和f(t)分别为APEWT分解后的各模态分量和原始信号;µfk,σfk,µf,σf分别为fk(t)和f(t)对应的时域均值和标准差;E为数学期望.ρf,fk反映了模态分量fk(t)与原始信号f(t)在时域中的相关性,其数值越大,表明模态分量与原始信号越相关,因此可根据ρf,fk的数值大小选择有效模态分量.
3.3 ES特征
对选出的模态按(3)式进行重构,信号重构后,由(7)式求取ES特征:

式中f2n指Trail中某通道信号重构后第n个采样点瞬时幅值的平方;EN表示求出的平均瞬时能量特征;fs为采样频率.当N
3.4 M S特征
Fourier频谱的某一点频率上的幅值表示在整个信号里有一个含有此频率的三角函数组分,而MS从统计意义上表征了整组数据每个频率点的累积幅值分布,MS能够处理非平稳信号,如果信号中某一频率的能量出现,就表示一定有该频率的振动波出现,所以MS能比较准确地反映信号的实际频率成分,而Fourier变换只能处理平稳信号,故文中使用MS特征.
对选出的IMF分量信号fk(t),(k=1,2,···,n)进行变换得

式中PV为柯西主值,则进一步得到zk(t)的解析式为
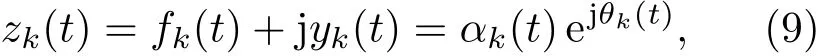
式中αk(t)代表瞬时幅值;θk(t)代表瞬时相位.希尔伯特变换的瞬时频率定义为

其希尔伯特谱定义为
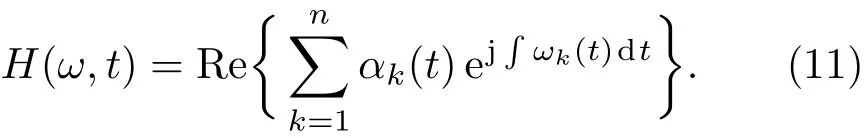
MS的定义为

式中T为信号长度.
3.5 选择集成分类模型
本文根据运动想象的ES特征和MS特征,采用选择集成分类模型对左右手运动想象EEG信号进行分类识别.
Huang等[25]提出了极限学习机(extreme learning machine,ELM)算法.该算法与BP(back propagation)等神经网络算法相比,大大提高了网络的泛化能力和学习速度,同时避免了陷入局部最优的风险.相比于ELM,支持向量机和最小二乘支持向量机更趋向于得到次优解,而且也都没有考虑多层前馈神经网络中隐层的特征表征[26].故本文将ELM作为选择集成分类模型的基分类器,单隐层前馈网络隐层节点个数为25,隐层激活函数为Sigmoid.
对于集成分类模型中权重的设置,假设每个基分类器对于训练集的分类正确率为A=[A1,A2,···,AM],权重计算式为
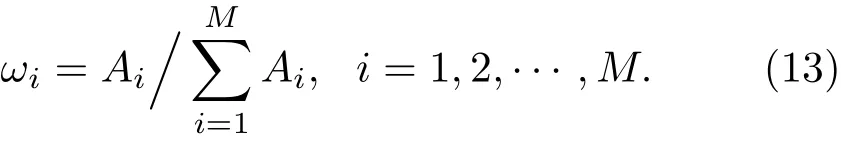
在集成分类模型中,若存在分类效果较差的基分类器将会影响最终的分类结果,所以本文对基分类器进行了选择.将基分类器训练集的准确率按照从大到小的顺序进行排列,以预测结果最优为原则,选择分类效果较好的α个基分类器,具体选择方法如下:
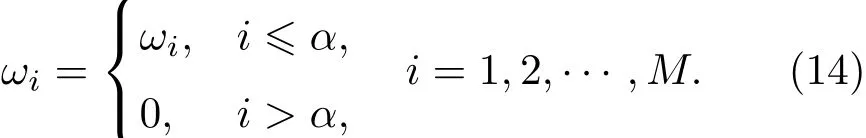
通过对基分类器的筛选,获得了较好的集成分类模型.假定有M个待集成的基分类器Ci(i=1,2,···,M),每个基分类器的预测标签结果为Ci(n),n为数据集中的样本数.选择集成分类模型为ˆC(n),则有
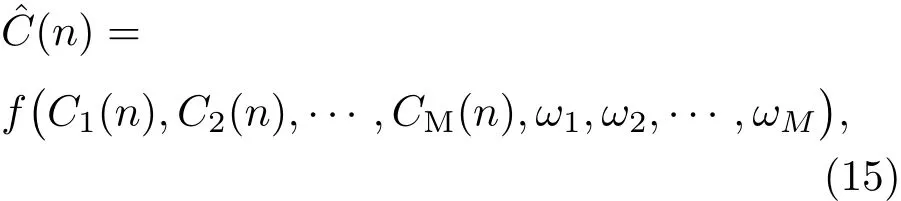
式中ωi满足f为集成规则.
具体的集成规则为:假设有k个基分类器的分类结果为左手,l个基分类器的分类结果为右手,其中k+l=M,若则集成分类器的结果为左手,否则为右手.
4 实验结果
本文方法的实验环境为Windows 64位系统,4 GB内存,CPU主频为1.80 GHz,仿真软件为MATLAB R2013 b.
4.1 信号分解与模态选择
受试者S1某一试次的运动想象EEG信号分别经EMD和APEWT分解后各阶模态分量和频谱图如图3所示.
由频域图3(b)和图3(d)可知,使用APEWT进行EEG信号分解的效果明显优于EMD.

图3 EEG信号分解结果 (a)EMD分解得到的IMF分量;(b)EMD分解的得到的IMF分量频谱;(c)APEWT分解得到的IMF分量;(d)APEWT分解的得到的IMF分量频谱Fig.3.EEG signal decomposition results:(a)EMD-based IMF components and(b)their corresponding frequency spectra;(c)APEWT-based IMF components and(d)their corresponding frequency spectra.

图4 运动想象EEG信号 (a)原始EEG信号;(b)重构后EEG信号Fig.4.EEG signals of motor imagery:(a)Original EEG signal;(b)reconstructed EEG signal.
基于(6)式计算并选取相关系数阈值ρf,fk>0.5[24],获得有效分量,分解后有效模态分量主要集中在f3,f4和f5分量上;同时由各分量的频谱图分析可知,mu节律和beta节律频段相应的信号也主要集中在f3,f4和f5分量上,从而选定这3个分量进行信号重构,原始信号和重构信号如图4所示.
4.2 ES特征和M S特征
为了更好地表现ES特征和MS特征C3和C4两个通道的关系,分别计算了6名受试者3—7 s的所有试次的ES特征和MS特征.运动想象EEG ES特征和MS特征分别如图5和图6所示.

图5 运动想象EEG ES特征 (a)左手运动想象;(b)右手运动想象Fig.5.ES features of motor imagery EEG:(a)Left motor imagery;(b)right motor imagery.

图6 运动想象EEG MS特征 (a)左手运动想象;(b)右手运动想象Fig.6.MS features of motor imagery EEG:(a)Left motor imagery;(b)right motor imagery.
4.3 分类结果与对比
为了验证本文方法的有效性,分别使用另外4种组合方法对两组运动想象脑电数据进行特征提取和分类.组合方法如表1所列,本文分别使用方法1和2对3—5 s,4—6 s和5—7 s三个不同时间段的EEG信号进行分类识别.其中,方法1和方法2将计算得到的特征进行重采样(128—4 Hz),从而得到了ELM的输入特征向量;方法3是对3—7 s的EEG信号进行分类识别,该方法分别对ES特征和MS特征进行重采样(128—4 Hz).最后,将两种特征作为ELM的输入特征向量;方法4中ELM输入特征向量的获取方法同本文方法(详见第3节).
图7(a)和图7(b)分别是使用方法1和方法2得到的6名受试者在3个不同时间段的分类正确率.使用方法1时,受试者S1—S5的最优时段为4—6 s,受试者S6的最优时段为3—5 s;使用方法2时,受试者S4的最优时段为3—5 s,其他受试者的最优时段为4—6 s.在最优时段分类正确率的对比中,受试者S1和S6在方法1中有较高分类正确率,受试者S2—S5在方法2中有优势.虽然在最优时段分类正确率的对比中,方法2优于方法1,但总体对比3个时间段的分类正确率可知,方法1优于方法2.在两种方法的对比分析中可知,不同受试者对ES特征和MS特征的敏感度存在差异,图7中显示的正确率均为测试集的平均分类正确率.
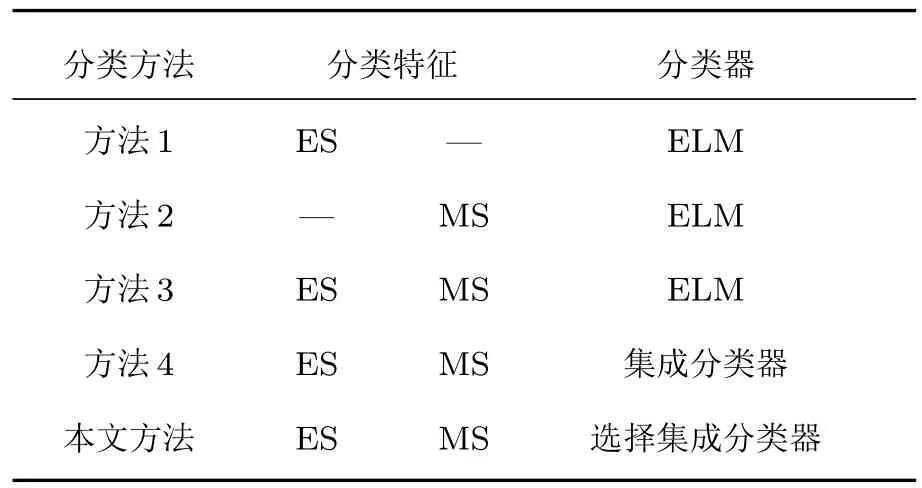
表1 不同方法的描述Table 1.Description of diff erent methods.
图8对比了6名受试者在3—7 s运动想象中5种不同方法的测试集的平均分类正确率.由图8可知,前3种方法各有优劣,后两种方法较前3种方法有优势,其中本文方法的分类正确率较前4种方法都高,有效证明了本文方法的有效性.同时,从图8可知,图中分类效果最好的为受试者S2,其平均分类正确率可达99.4%,分类效果较差的受试者为S3和S4,其平均分类正确率分别是77%和79.5%.
为了更好地验证本文方法的有效性,本文不仅采用了识别率,同时使用受试者工作特征(receiver operating characteristic,ROC)曲线对分类模型性能进行评估,6名受试者的ROC曲线如图9所示.从图中可以比较明显地看出,本文方法的ROC曲线下面积(area under the ROC curve,AUC)明显大于其他方法,进一步验证了本文方法的有效性.

图7 不同时段分类正确率的误差条形图 (a)方法1;(b)方法2Fig.7.Error bar chart of classifi cation accuracy with diff erent time:(a)Method 1;(b)method 2.

图8 5种方法分类正确率的误差条形图Fig.8.Error bar chart of classifi cation accuracy with fi ve methods.

图9 6名受试者在五种方法下对测试集分类生成的ROC曲线Fig.9.ROC curves generated by classifi cation of test sets by six subjects with fi ve methods.
5 讨 论
如何提高具有非平稳性和非线性运动想象EEG信号的识别率是运动想象类脑机接口的关键之一.目前,研究者已经提出了很多运动想象脑电特征的提取方法,本文在前人研究的基础上,提出了基于APEWT和选择集成分类模型的运动想象模式识别方法.该方法从运动想象伴随的ERD现象入手,根据不同时段和频段特征的分类效果为其分配不同的权值,综合考虑了多个时段和频段的特征,从而避免了单一时段或频段数据分析的不准确性和局限性.
图5和图6中两种特征的分布情况符合ERD原理,这也再次证明了在运动想象期间发生了ERD这一现象.同时,从图中可以明显看出,受试者S3的ERD现象最不明显,这可能是受试者S3的分类正确率最差的原因.
从图7可以看出,不同时段和不同受试者有着不同的分类正确率.其中,大多受试者在4—6 s时间段内的识别率最高,可能是因为在3—5 s期间为运动想象执行的初始阶段,受试者心理活动有一个滞后和适应的过程,在4—6 s期间,被试运动想象活动质量较好;6 s以后为运动想象执行的最后时间,被试者的运动想象心理活动质量有所下降,分类正确率相对较低.从图7也可看出,不同的受试者可能会有着不同的的最优时段,不同的受试者对ES和MS两种特征的敏感程度也不同,由此可知,如果将两种特征进行有效融合,可能将有效提高分类效果.
由图8可知,在最优时段中,方法2较方法1有优势,在相同分类器情况下,MS特征比ES特征具有更好的分类效果.方法3虽然使用了ES特征和MS特征,但其分类效果并不理想,主要原因可能是没有选择最优时段的ES特征和最优频段的MS特征,其特征向量中含有太多不相关特征影响了其分类正确率.
由图9可知,本文方法和方法4的AUC值明显大于方法3.同时从方法3,4和本文方法分类正确率的对比中可以发现,在相同特征情况下,集成分类器优于ELM,选择集成分类器要优于非选择集成分类器,主要原因可能是:1)在集成分类器中,考虑了EEG信号不同时段ES特征和频段MS特征的差异性,并根据其不同的训练效果为其分配相应的权重,有效降低了较差特征对分类结果的影响;2)相比非选择集成分类器,选择集成分类器剔除了分类性能较差的基分类器,提高了分类模型的识别率,从而得到了较好的分类效果.

表2 不同受试者的平均正确率/%Table 2.Average accuracy of diff erent subjects/%.
此外,为进一步验证本文方法的有效性,还将本文方法所得正确率与使用相同数据集的近期文献进行了对比.文献[10]使用HHT对5.5—7.5 s的EEG信号进行分解,综合考虑了ES特征和AR模型系数;文献[27]应用了FBCSP(fi lter bank common spatial pattern)算法提取了3—7.5 s运动想象的特征,没有在FBCSP中执行特征选择,而是使用了随机森林分类器;文献[28]使用了相应频带的Hjorth参数特征,表2中的正确率分别发生在5—6 s,7.5—8.5 s,5.5—6.5 s,6—7 s和5—6 s.表2比较了本文方法与这些文献的平均分类正确率,受试者S1的平均分类正确率比文献[10]提高了14.49个百分点,且高于BCI竞赛中第一名的89.29%,后5名受试者的平均分类正确率为88.83%,比文献[27]高出3.75个百分点,比文献[28]高出3.41个百分点.本文方法在受试者S1,S2,S4,S5和S6的识别率都有所提高,进一步验证了本文方法有效性和普适性.
表3为单次运动想象分类过程的时耗,实验中,单次特征提取的时间为3—7 s.本文方法中时耗最长的是APEWT过程,本文方法的总时耗为0.2997 s,表明本文方法具有较好的实时性,适合在线BCI.

表3 本文方法的时耗统计Table 3.Time consumption of the method used in proposed method.
6 结 论
应用APEWT方法对EEG信号进行分解,使用最优模态重构后的信号得到ES特征,使用最优模态分量得到MS特征,通过加窗方法获得了不同时段的ES特征和不同频段的MS特征.根据不同时段和频段特征的分类效果为其分配不同的权重,通过构建的选择集成分类模型得到了较好的分类结果,其分类模型具有较好的分类性能和泛化能力.实验中6名受试者的平均分类正确率为89.95%,单次运动想象分类过程的总时耗为0.2997 s,其平均分类正确率与近期其他文献相比有明显优势,有效验证了本文方法的有效性,为以后在线运动想象类BCI提供了新的方法.在本文基础上,下一步的研究计划是进一步完善本文方法并将其应用到实际的在线BCI中.
[1]Zhang D,Li J W 2017 Sci.Technol.Rev.35 62(in Chinese)[张丹,李佳蔚 2017科技导报 35 62]
[2]Gao S,Wang Y,Gao X,Hong B 2014 Trans.Biomed.Eng.61 1436
[3]Abdulkader S N,Atia A,Mostafa M S M 2015 Egy.Inf.J.16 213
[4]Fang X L,Jiang Z L 2007 Acta Phys.Sin.56 7330(in Chinese)[方小玲,姜宗来 2007物理学报 56 7330]
[5]Pfurtscheller G,da Silva F H L 1999 Cli.Neurophysiol.110 1842
[6]Lei M,Meng G,Zhang W M,Nilanjan S 2016 Acta Phys.Sin.65 108701(in Chinese)[雷敏,孟光,张文明,Nilanjan Sarkar 2016物理学报65 108701]
[7]Lei M,Meng G,Zhang W M,Joshua W,Nilanjan S 2016 Entropy 18 412
[8]Wang Y,Hou F Z,Dai J F,Liu X F,Li J,Wang J 2014 Acta Phys.Sin.63 218701(in Chinese)[王莹,侯凤贞,戴加飞,刘新峰,李锦,王俊2014物理学报63 218701]
[9]Xu B,Song A 2008 J.Biomed.Sci.Eng.1 64
[10]Sun H W,Fu Y F,Xiong X,Yang J,Liu C W,Yu Z T 2015 Acta Automatica Sin.41 1686(in Chinese)[孙会文,伏云发,熊馨,杨俊,刘传伟,余正涛 2015自动化学报41 1686]
[11]Xie P,Chen X L,Su Y P,Liang Z H,Li X L 2013 Chin.J.Biomed.Eng.32 641(in Chinese)[谢平,陈晓玲,苏玉萍,梁振虎,李小俚2013中国生物医学工程学报32 641]
[12]Yang M H,Chen W Z,Li M Y 2017 Acta Automatica Sin.43 743(in Chinese)[杨默涵,陈万忠,李明阳2017自动化学报43 743]
[13]Wu L Y,Lu H,Gao N,Wang T 2017 Chin.J.Biomed.Eng.36 224(in Chinese)[吴林彦,鲁昊,高诺,王涛 2017生物医学工程研究36 224]
[14]Zhang X Q,Liang J 2013 Acta Phys.Sin.62 050505(in Chinese)[张学清,梁军 2013物理学报62 050505]
[15]Tang Z C,Sun S Q,Zhang K J 2017 Chin.J.Mech.Eng.53 60(in Chinese)[唐智川,孙守迁,张克俊2017机械工程学报53 60]
[16]Gilles J 2013 IEEE Trans.Signal Proc.61 3999
[17]Gilles J,Heal K 2014 Multiresol.Inf.Proces 12 1450044[18]Zheng J,Pan H,Yang S,Cheng J 2017 Signal.Proces 130 305
[19]Hou B W 2012 M.S.Dissertation(Xi’an:Xidian University)(in Chinese)侯秉文 2012硕士学位论文 (西安:西安电子科技大学)
[20]Zhao Y,Chen R,Liu W 2016 Comput.Sci.8 177(in Chinese)[赵宇,陈锐,刘蔚2016计算机科学 8 177]
[21]BCI Competition II http://www.bbci.de/competition/ii/[2018-1-15]
[22]BCI Competition IV http://www.bbci.de/competition/iv/[2018-1-15]
[23]Lindeberg T,ter Haar R B M 1994 Linear Scale-Space I:Basic Theory(Netherlands:Springer)pp1–38
[24]Cai Y P,Li A H,Wang T,Yao L,Xu P 2010 J.Vibra.Eng.4 430(in Chinese)[蔡艳平,李艾华,王涛,姚良,许平2010振动工程学报4 430]
[25]Huang G B,Zhu Q Y,Siew C K 2004 IEEE International Joint Conference on Neural Networks Proceedings Budapest,Hungary,July 25–29,2004 p985
[26]Huang G B,Zhu Q Y,Siew C K 2006 Neurocomput 70 489
[27]Bentlemsan M,Zemouri E T T,Bouchaff ra D,Yahya-Zoubir,B,Ferroudji,K 2014 5th International Conference on Intelligent Systems,Modelling and Simulation,Langkawi,Malaysia,Jan.27–29,2014 p235
[28]Suk H I,Lee S W 2013 Trans.Patt.Anal.Mach.Intelli 35 286
