考虑定位力及波纹力的电磁悬架作动器波动力抑制方法

杨 超 李以农，2 胡一明 钟银辉

1.重庆大学汽车工程学院，重庆，400030 2.重庆大学机械传动国家重点实验室，重庆，400030

0 引言

轮边驱动电动汽车由于具有结构布置灵活、传动链短和效率高的特点，已经成为电动汽车发展的新方向；但轮边驱动系统因簧下质量的增大，造成了车辆的平顺性和操稳性恶化［1-3］，目前主要采用主动悬架技术解决这一问题。针对主动悬架的研究主要集中于控制策略及算法的制定［4-6］，对悬架作动器的研究较少。

文献［7-8］采用旋转电机通过齿轮齿条或滚珠丝杆等传动机构将旋转运动转化为直线运动。该装置能够将电机旋转产生的动力转化为直线的推力以实现悬架减振的目的，同时能够将路面的振动能量转化为电能进行存储，但其传动链较长，效率较低，且齿轮啮合易出现松动进而降低了系统的稳定性及增加了误差。文献［9］利用电磁感应原理设计了一款直线式感应作动器，电磁力最大可达到550 N，但线圈电流高达42A，作动器发热严重，效率低。文献［10］利用开关磁阻电机的原理设计了一种磁阻式直线作动器，采用4组单元电机并联的方式增大了电磁力，但该作动器体积大，且采用双凸极结构设计会造成严重的推力波动。文献［11-12］采用稀土永磁体设计了永磁式直线作动器，极大地增大了电磁作动力的输出，减小了作动器的体积，并且优化了作动器结构和形状，满足在车辆上紧凑布置的要求；但此类直线作动器均忽略了齿槽结构、端部效应以及磁场谐波带来的电磁力波动的问题，直接影响控制器设计。文献［13］分析了引起直线式电机推力产生波动的主要成分。

本文针对轮边驱动电动汽车电磁悬架系统，设计了一种新型基于分数槽的永磁直驱式的悬架作动器，理论解析磁场中绕组的磁链及感应电动势，运用有限元方法分析作动器的电磁力输出特性，重点研究造成电磁力波动的因素，并对各因素对应的结构参数进行改进，最终达到抑制电磁力波动的目的。

1 电磁悬架介绍及作动器设计

图1为作动器结构示意图。在电磁悬架系统中，作动器初级铁心（定子）与轮轴、轮毂、电机和轮胎等簧下质量相连，次级铁心（动子）与车架等簧上质量相连，初级和次级铁心在电流激励下产生相对运动和电磁阻尼力。此外，被动工作时初级铁心绕组在次级磁场中产生感应电动势，通过馈能电路向蓄电池充电，进而能够实现能量回收。

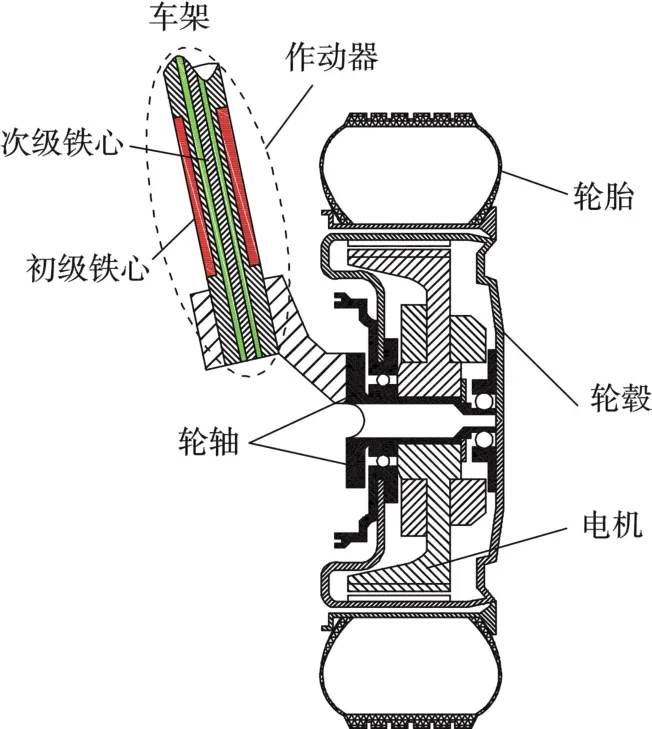
图1 作动器结构示意图Fig.1 Schematic diagram of the actuator

为满足作动器行程以及便于在试验车上的安装，对作动器的外形尺寸进行限制：圆筒形作动器初极外径不超过80 mm；考虑到槽型设计和绕组的安装，参考文献［14］选择次级外径和初级外径比值约为0.5；初级铁心长度不超过190 mm；气隙长度选择1 mm；槽型选择平底槽。为方便绕组线圈的灵活布置，槽数选用偶数槽［15］，结合作动器尺寸本文选择12槽，匹配的磁极对数见表1。

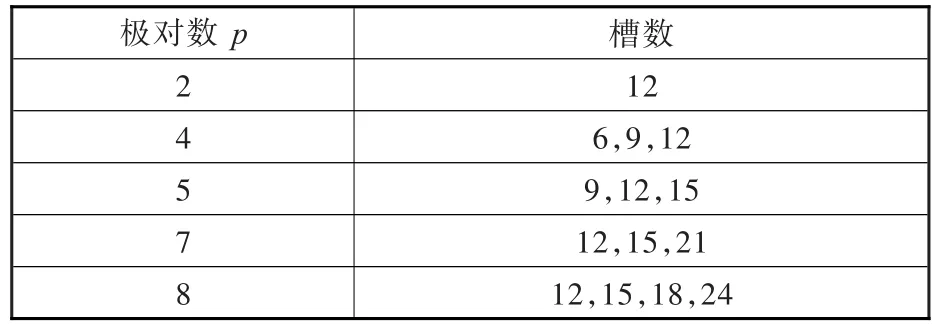
表1 作动器极槽匹配Tab.1 Slot/Pole combinations of actuator

由表1可以看出，12槽可对应4极、8极、10极、14极和16极，其中12槽4极为整数槽结构，其余为分数槽结构。为避免作动器有较大推力波动，本文选用分数槽，而在分数槽结构中选择绕组系数最大的12槽14极结构［15］，作动器具体结构参数见表2。作动器定子布置三相绕组，基于感应电动势正弦性原则，电枢绕组采用双层绕组设计，如图2所示。图中A、B、C代表各相正向绕组线圈，a、b、c代表负向绕组线圈。

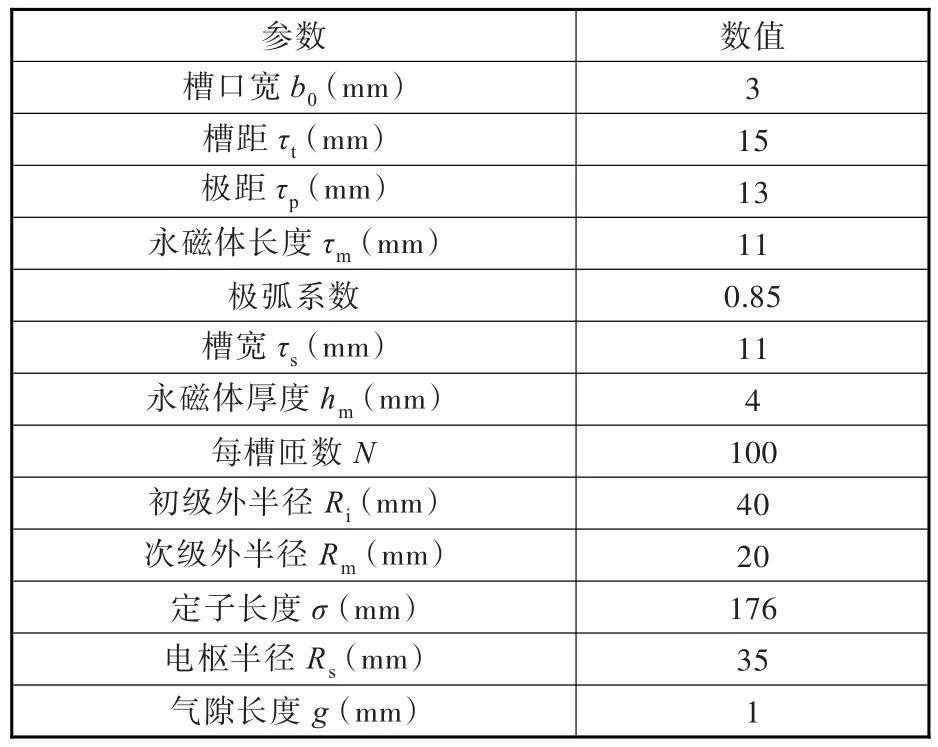
表2 作动器结构参数Tab.2 Structural parameters of the actuator

图2 作动器绕组分布Fig.2 Winding distribution of the actuator

2 模型的建立及验证

2.1 磁场解析模型

感应电动势是衡量电磁作动器电磁力输出和馈能性能的主要参数之一。为分析本文所设计永磁直线作动器性能，参考文献［16］建立作动器磁场计算模型。图3为圆筒形作动器结构尺寸示意图，其中，横坐标z为作动器轴向长度，纵坐标r为作动器径向长度。作动器结构的具体数值见表2，其中τcp为线圈节距，本文齿距和节距相同。

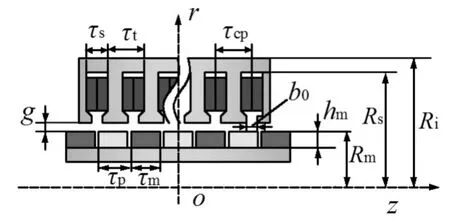
图3 作动器结构尺寸示意图Fig.3 Schematic size diagram of the actuator

由于采用齿槽结构设计，引入卡特系数Kc：

式中，g′为考虑了齿槽效应的作动器气隙长度；μr为相对磁导率，取1.04；γ为齿槽系数。

气隙有效计算长度ge表示为

有效电枢厚度Rse为

单相磁链Φ可按下式计算：

式中，Φnp为第n次磁链的幅值；mn为第n次磁链的角频率；z为作动器到O点的移动距离；Kdpn为作动器绕组系数；Krn为气隙磁场分布系数；Nc为每槽每相匝数；p为极对数；Kdn、Kpn分别为绕组分布系数和短距系数；aIn、bIn为一类贝塞尔函数 BI1(⋅)和 BK1(⋅)的系数，计算过程见文献［17］。

每相绕组感应电动势表示为

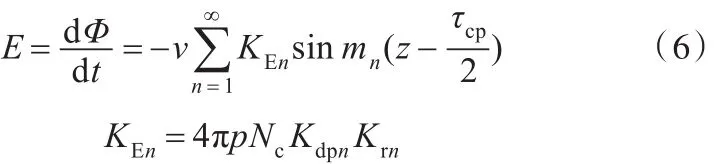
式中，v为作动器运动速度。

2.2 有限元模型

根据表2结构参数，在Ansoft Maxwell电磁仿真软件中建立作动器几何及有限元模型；对各部分材料属性进行设置，作动器动子和定子铁心采用冷轧硅钢片叠制而成，型号为DW465_50；永磁体为钕铁硼（NdFeB），型号为N30，其中矫顽力Hc=838 kA/m，剩余磁通密度Br=1.1T，永磁体充磁方式为径向充磁。绕组为铜线，直径为1 mm，气隙空间设置为真空；对各部分进行网格划分；进行直线作动器分析时，在作动器运动的区域外施加Balloon气球边界。由于本文作动器为对称结构，故建立关于Z轴旋转对称的模型，如图4所示。

图4 作动器几何模型及有限元网格模型Fig.4 Geometric model and finite element mesh model of actuator

此外，在建立的有限元模型中设置作动器电源激励为0，设置一定的运行速度，可以仿真空载绕组感应电动势。设定作动器运行速度为0.2 m/s。单相磁链的理论值和有限元值计算如图5所示，绕组感应电动势曲线如图6所示。

由图5可以看出，一个运动周期内（2个极距）磁链基本上呈现正弦分布，磁链最大值为0.13Wb，且理论值和有限元值基本一致。由图6可以看出，感应电动势波形有限元计算结果和理论计算结果同样吻合良好，感应电动势最大值为7.2V。

图5 单相绕组磁链Fig.5 One phase winding flux-linkage

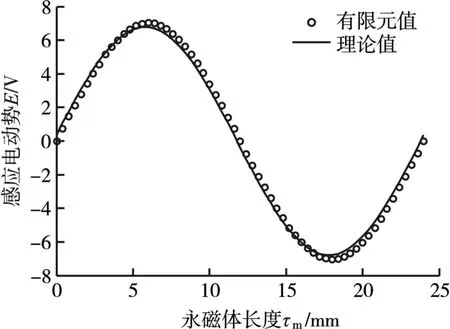
图6 绕组感应电动势曲线Fig.6 Winding induced electromotive force curve

图7所示为悬架常用工作速度在0～1 m/s范围内感应电动势幅值计算结果。由图7可以看出，随着速度的增大，感应电动势幅值基本上呈线性增大，斜率约为36 V/（m·s-1）。结合图5～图7的结果可知，电机作动器绕组磁链、感应电动势的波形及其幅值的有限元值和理论值计算均相符，因此证明了所设计作动器模型的正确性。

图7 绕组感应电动势幅值随速度变化Fig.7 Winding induced electromotive force amplitudes with the changes of the speeds

3 作动器电磁力分析及波动的抑制

3.1 电磁力分析

相比于传统减振器减振力特性，电磁悬架的电磁力（减振力）可随电流的大小和速度的大小进行实时调节。对上述有限元模型进行电磁力瞬态分析。设定作动器的同步速度为0.2 m/s，峰值电流为3.5 A，输入三相交流电：

式中，ω为电流角频率；f为电流的频率；φ为初相位角。

电磁力计算时间为200 ms，其计算结果如图8所示。由图8可以看出，作动器电磁力输出并非是稳定的数值，存在一定周期性的波动，其中最大值为269.5 N，最小值为164.8 N，波动差值为104.7 N。这种波动会造成电磁力的控制精度降低，影响整车的舒适性和安全性；同时也会引起系统的结构振动，降低系统的可靠性，因此，必须对其进行有效的抑制。

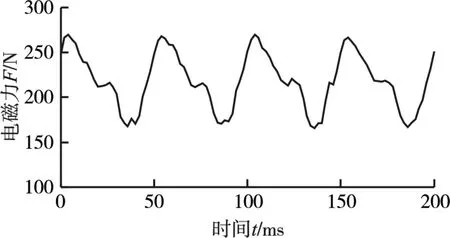
图8 作动器电磁力Fig.8 Electromagnetic force of actuator

3.2 定位力分析

电磁力波动主要是由作动器空载时的定位力以及负载时的波纹力共同作用而产生。图9所示为空载运行时作动器定位力波动曲线，可以看出，上下幅值差为99.6 N。

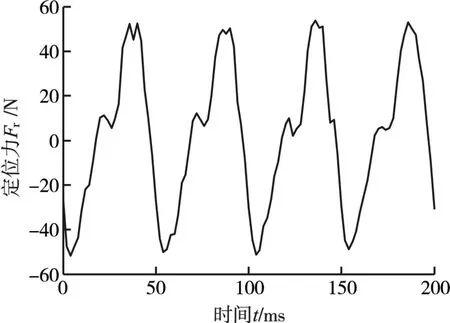
图9 空载定位力波动曲线Fig.9 Curves of cogging force in no-load

定位力主要包含端部力和齿槽力，由于本文作动器结构采用12槽14极的分数槽结构，齿槽力已较小［13］，因此主要分析端部力。F-、F+分别为作动器两端所受端部力，两者方向相反。对于任意长度的定子铁心，F-和F+的关系可表达为

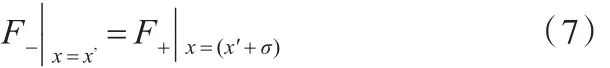
式中，σ为定子长度；x′为一端的起点。

将右端端部力进行傅里叶级数展开：

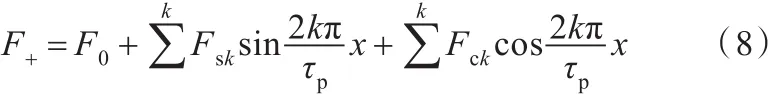
式中，F0为端部力的直流分量；Fsk、Fck为第k阶傅里叶分解系数。

总的端部力为F+和F-之和，合力可表示为

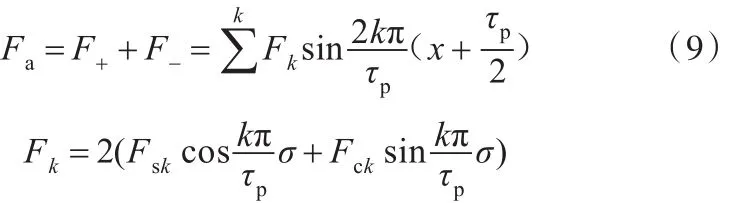
由式（9）可知，端部力与定子长度有关，因此，选择合适的定子长度可有效地减小端部力。令Fa=0，由于定子位置一直处于变化中，故正弦函数前面的系数Fk=0，即

由式（10）可知，当，端部力最小。对定子长度σ进行参数化分析，可通过增加两端端部齿的长度L0来改变定子的长度，使作动器定位力达到最小，如图10所示，其分析结果如图11所示。

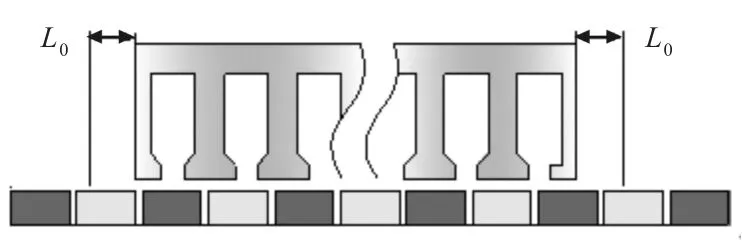
图10 端部齿增加长度Fig.10 Incremental length of end tooth

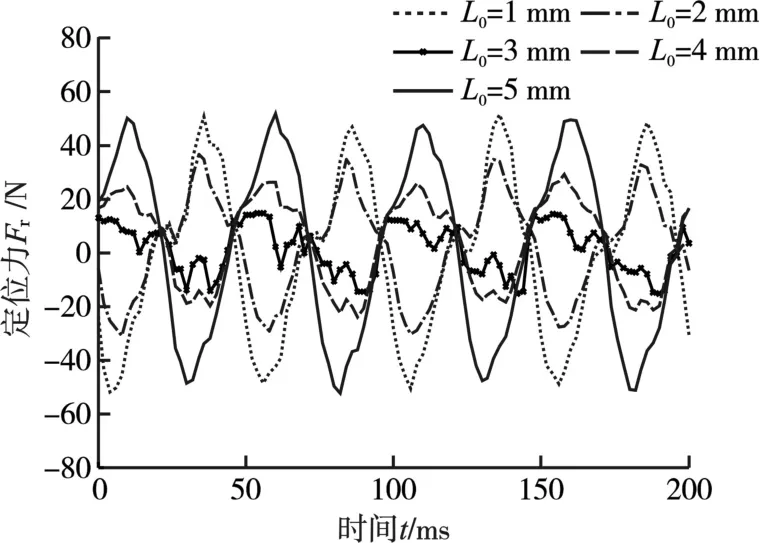
图11 端部齿增加的长度对定位力的影响Fig.11 Contrasts of cogging force waves with different incremental length

由图11可以看出，随着端部齿长度的增加，定位力先减小后增大，当L0=3 mm时（约为极距长度的0.23倍）作动器定位力最小，上下幅值差为24.0N。文献［13］中指出，当 L0=0.25τp时端部力最小，基本验证了本文结果的正确性。结合表2中定子初始长度为176 mm，加上改进后的端部齿增加的长度，则可得出最小定位力对应的定子长度为182 mm。图12所示为作动器原型定子长度和改进定子长度后的作动器定位力对比，可以看出，原型作动器定位力幅值差为99.6 N，改进定子长度后的作动器定位力幅值差为24.0 N，减小了75.6 N。

图12 定子长度改进前后定位力对比Fig.12 Contrasts of cogging force with initial and after optimization of stator

3.3 波纹力分析

上述对端部力的抑制是在作动器空载的情况下进行的，而在负载条件下，作动器电磁力可以表示为

式中，P为作动器输入功率；EA、EB、EC为三相感应电动势。

在理想的正弦感应电动势和三相电流作用下的作动器电磁力基本无推力波动，但实际上作动器结构的绕组感应电动势并不是完全正弦，含有谐波分量，在与输入的电流作用下产生波纹力，进而造成电磁力波动。由于仿真输入的电流激励为理想正弦波，因此本文对波纹力的优化着重从作动器感应电动势所含谐波方面进行分析。用各谐波所占基波比η来评价各谐波分量，表示为

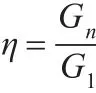
式中，Gn为第n次谐波分量有效值；G1为基波分量有效值，由于高次谐波所占基波比值较低，这里n取到5。

图13所示为原型作动器的感应电动势的谐波分量。由图13可知：除基波外感应电动势谐波主要存在3次、2次、4次和5次等谐波分量，其中3次谐波分量所占基波比例最大，为4.2%，2次谐波、4次谐波和5次谐波所占基波比分别为3.1%、1.9%和1.3%。

影响感应电动势波形的主要参数为永磁体的长度以及槽口宽度等。作动器在设计阶段已对永磁体极弧系数进行了合理的选取，因此本文只针对槽口宽度进行改进。针对不同的槽口宽度对感应电动势波形的影响，以总谐波畸变率THD值进行评价，其中THD计算如下：

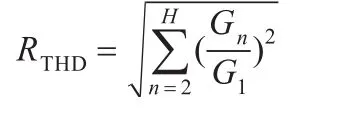
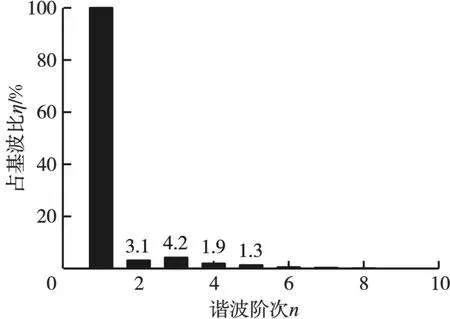
图13 感应电动势谐波分量Fig.13 Harmonic components of induction electromotive force

式中，H为指定阶次数，这里H取到5。

图14所示为THD值随槽口宽度的变化。由图14可以看出，当槽口开度从3 mm逐渐增大到6 mm的过程中，THD值先减小后增大；当槽口开度为4.5 mm时，作动器感应电动势THD值最小，为4.5%。

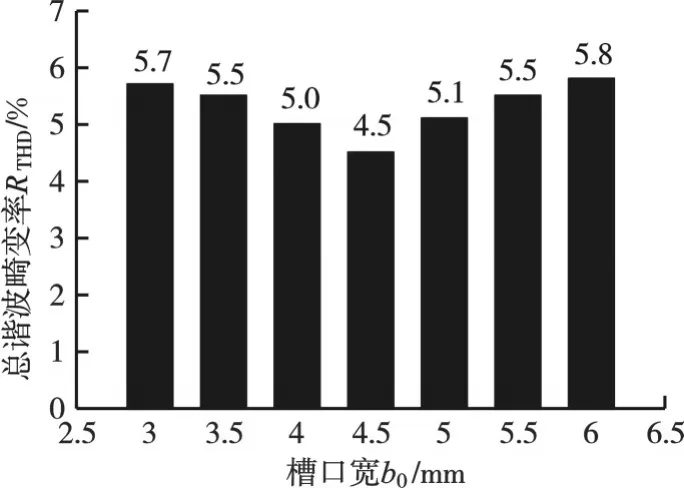
图14 槽口宽度变化对感应电动势THD值影响Fig.14 Effect of slot width changes on induction electromotive force THD

图15所示为改进后槽口为4.5 mm时电磁力与改进前槽口为3 mm的作动器（即改进定子长度后的作动器）在输入3.5 A电流时的电磁力对比。由图15可以看出，改进后作动器电磁力略小于改进前作动器电磁力，主要是因为改进槽宽后，增大了气隙间的漏磁，进而造成作动器电磁力减小。为准确分析电磁力及其波动的变化，以电磁力的有效值作为电磁力的计算值，以波动的最大值与最小值之差作为波动值，计算结果如表3所示。由表3可以看出，改进后作动器电磁力的计算值较改进前作动器电磁力的计算值减小了7.2N，降幅约为3.3%；波动值减小了3.2 N，降幅约为13.3%。波动值的减小幅度要远大于电磁力的计算值减小的幅度。

对上述两种减小电磁力波动的措施进行综合分析，原型作动器电磁力空载波动值为99.6 N，通过减小端部力，减小了75.6 N。在此基础上通过减小波纹力，减小了3.2 N。改进后电磁力负载情况下波动值仅为20.8 N，较原型作动器负载下波动104.7 N相比，削减电磁力波动80.1%，取得了明显的效果。此外还可以看出，定位力（主要是端部力）是电磁力波动的主要成分。

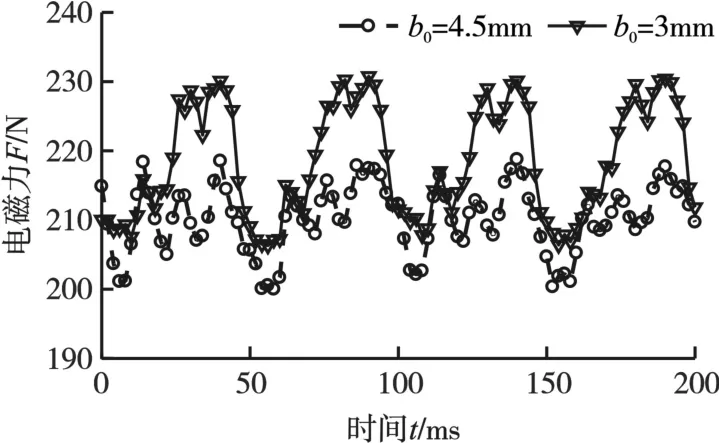
图15 改进前后电磁力波动对比Fig.15 Contrasts of electromagnetic force ripple with before and after optimization

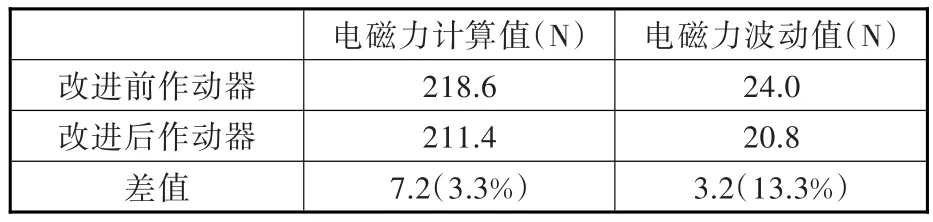
表3 电磁力波动减小参数表Tab.3 Distribution table of electromagnetic force ripple reduction

4 结论

（1）在电磁力分析中发现：负载情况下，当输入3.6A三相正弦交流电时电磁力波动值为104.7 N；空载情况下定位力为99.6 N。

（2）在结构参数化分析中发现：随着定子长度的增加，作动器定位力先减小后增大，当定子长度为182 mm时，定位力最小为24.0 N；随着槽口宽度的增大，感应电动势谐波THD值先减小后增大，且当槽口宽度为4.5 mm时，THD值最小为4.5%，同时对应最小电磁力波动值为20.8 N。

（3）在抑制电磁力波动分析中发现：通过改进定子长度，定位力减小了75.6 N；通过改进槽口宽度，波纹力仅减小了3.2 N。由此，通过减小定位力来抑制电磁力波动更为有效，可为后续类似结构的作动器波动力的抑制作指导。

［1］ MURATTA S.Innovation by In-wheel-motor Drive Unit［J］.Vehicle System Dynamics，2012，50（6）：807-830.

［2］ WANG Y Y，LI Y N，SUN W，et al.Effect of The Unbalanced Vertical Force of a Switched Reluctance Motor on the Stability and the Comfort of an In-wheel Motor Electric Vehicle［J］.Proc.IMechE Part D：Journal of Automobile Engineering，2015，229（12）：1569-1584.

［3］ KANGHYU N，FUJIMOTO H，HORI Y.Lateral Stability Control of In-wheel-motor-driven Electric Vehicles Based on Sideslip Angle Estimation Using Lateral Tire Force Sensors［J］.IEEE Transactions on Vehicular Technology，2012，61（5）：1972-1985.

［4］ THUL A，EGGERS D，RIEMER B，et al.Active Suspension System with Integrated Electrical Tubular Linear Motor：Design，Control Strategy and Validation［J］.Archives of Electrical Engineering，2016，64（4）：605-616.

［5］ WANG W，SONG Y L，XUE Y B，et al.An Optimal Vibration Control Strategy for a Vehicle's Active Suspension Based on Improved Cultural Algorithm［J］.Applied Soft Computing，2015，28：167-174

［6］ 裴金顺，李以农，王艳阳，等.采用电磁直线电机的主动悬架控制系统的设计与能量分析［J］.汽车工程，2014，36（11）：1386-1391.PEI Jinshun，LI Yinong，WANG Yanyang，et al.Design and Energy Analysis of an Active Suspension Control System with Electromagnetic Linear Motor［J］.Automotive Engineering，2014，36（11）：1386-1391.

［7］ ZHANG G G，CAO J Y，YU F.Design of Active and Energy-regenerative Controllers for DC Motor-based Suspension［J］.Mechatronics，2012，22（8）：1124-1134.

［8］ HUANG B，HSIEH CY，GOLNARAGHI F，et al.Development and Optimization of an Energy-regenerative Suspension System under Stochastic Road Excitation［J］.Journal of Sound and Vibration，2015，357：16-34.

［9］ 邓兆祥，来飞.车辆主动悬架用电磁直线作动器的研究［J］.机械工程学报，2011，47（14）：121-128.DENG Zhaoxiang，LAI Fei.Electromagnetic Linear Actuator for Vehicle Active Suspension［J］.Journal of Mechanical Engineering，2011，47（14）：121-128.

［10］ LIN J K，CHENG K W E，ZHANG Z，et al.Active Suspension System Based on Linear Switched Reluctance Actuator and Control Schemes［J］.IEEE Transactions on Vehicular Technology，2013，62（2）：562-572.

［11］ 杨超，李以农，钟银辉，等.一种分数槽结构的悬架直线作动器及性能分析［J］.上海交通大学学报，2016，50（6）：837-843.YANG Chao，LI Yinong，ZHONG Yinhui，et al.A Tubular Permanent Magnet Linear Actuator Based on Fractional Slot and Performance Analysis［J］.Journal of Shanghai Jiaotong University，2016，50（6）：837-843.

［12］ BART L J G，JEROEN L G J，JOHANNES J H P，et al.Design Aspects of an Active Electromagnetic Suspension System for Automotive Applications［J］.IEEE Transactions on Industry Applications，2010，45（5）：1589-1597.

［13］ WANG Q，WANG J B.Assessment of Coggingforce-reduction Techniques Applied to Fractional-slot Linear Permanent Magnet Motors Equipped with Non-overlapping Windings.［J］.LET Electric Power Applications，2016；10（8）：697-705.

［14］ WANG J B，DAVID H.Tubular Modular Permanent-magnet Machines Equipped with Quasi-halbach Magnetized Magnets—Part I：Magnetic Field Distribution，EMF，and Thrust Force［J］.IEEE Transactions on Magnetics，2005，41（9）：2470-2478.

［15］ 谭建成.永磁无刷直流电机技术［M］.北京：机械工业出版社，2011：93-97.TAN Jiancheng.Technology of Permanent Magnet Brushless DC Motor［M］.Beijing：China Machine Press，2011：93-97.

［16］ WANG J B，GERAINT W J，DAVID H.A General Framework for the Analysis and Design of Tubular Liear Permanent Magnet Machines［J］.IEEE Transactions on Magnetics，1999，35（3）：1986-2000.

［17］ WANG J B，DAVID H.Design Optimization of Radially Magnetized，Iron-cored，Tubular Permanent-magnet Machines and Drive Systems［J］.IEEE Transactions on Magnetics，2004，40（5）：3262-3277.