带槽口缺陷的圆钢管短柱轴压性能试验

顾宏伟， 陈 誉

(福州大学土木工程学院， 福建 福州 350108)

0 引言

圆盘锯切割圆钢管是一种比较普遍的切割工艺， 不同的切割工艺会产生不同的缺陷. 由于锯片偏摆、 机器反复振动、 垫板损耗、 行程受限锯多刀和圆钢管切割滑动等因素影响， 使用圆盘锯切割的圆钢管会带有多种缺陷， 其中槽口缺陷最为典型. 在实际工程中， 圆钢管常常由于钢管切割缺陷的问题而被直接更换， 导致经济成本增加； 由于圆钢管切割缺陷的问题而进行二次切割及抛光， 致使时间成本增加. 因此， 对带有切割缺陷的圆钢管短柱进行力学性能研究， 从而探索钢管切割缺陷的容许值具有重要工程意义.

目前， 国内外学者对带有初始缺陷的钢管提出了不少探伤方法， 进行系列探伤研究[1-3]. 有关焊管的规范[4-6]也与时俱进， 但仍然无法完全避免钢管缺陷. 为此， 学者们在初始缺陷对钢管性能影响方面展开大量科学试验， 取得了一些研究成果. 韩少华等[7]发现宽厚比以及初始缺陷裂缝长度对不锈钢方钢管短柱承载力影响较大， 对其延性和刚度下降速率基本无影响. 温晓飞等[8]通过试验研究了几何缺陷对双向偏压作用下矩形钢管混凝土柱受力性能影响. 王志滨等[9-11]研究了不同用途下缺陷对钢管混凝土构件的影响. 吕利芹等[12]以人工槽口模拟钢管的初始缺陷， 得出横向缺陷对试件受弯承载力的削减大于纵向缺陷的结论. 郭展等[13]对带初始缺陷的拉挤型GFRP管轴压性能展开了试验研究. 王小平等[14-15]运用有限元软件并参考规范[16-17]， 确定了中厚壁冷弯方钢管轴心压杆稳定系数的初步确定方法. 陈宏远等[18]分析了受初始几何缺陷影响的管线钢管在内压作用下的非线性屈曲. 于雪松[19]探讨了不同GFRP管壁厚度、 不同混凝土强度等级、 不同钢筋配置、 不同纤维缠绕角度、 不同开孔位置和不同开孔尺寸对集合缺陷柱力学性能影响. Liu等[20]通过对六角组合柱的研究， 发现轴压荷载作用下， 水平切口的柱会切口封闭而屈曲， 垂直切口的柱会向外弯曲而屈曲. Chang等[21]和Ding等[22]讨论了带切口缺陷的CFT试件轴压荷载下的荷载-位移响应、 柱强度和约束效应， 并对切口长度、 切口方向、 混凝土强度和配筋率等进行了参数研究.

目前国内外学者对初始缺陷的研究多局限于构件质量不均匀、 残余应力以及初始几何缺陷等， 而带有切割缺陷的圆钢管短柱轴压力学性能的研究并未见到报道. 本研究通过对带槽口缺陷的圆钢管短柱进行轴压性能试验， 分析槽口缺陷高度、 单双端缺陷以及壁厚对圆钢管短柱的破坏模式和极限承载力的影响.

1 试验设计

1.1 试件设计

本次试验将6根直径为168 mm， 长度为6 000 mm， 壁厚为2.5 mm的Q235圆钢管和6根直径为168 mm， 长度为6 000 mm， 壁厚为4.0 mm的Q235圆钢管使用圆盘锯切割， 可得到72根直径为168 mm， 长度为420 mm， 壁厚为2.5 mm的圆钢管和72根直径为168 mm， 长度为420 mm， 壁厚为4.0 mm的圆钢管. 从2×72根圆钢管中筛选出带槽口缺陷的钢管， 使用游标卡尺对圆钢管端部槽口缺陷高度进行精准测量. 根据测量数据的大小进行排序并标号， 试件长度为L/mm， 直径为d/mm， 壁厚为t/mm， 圆钢管短柱两端分别为A和B， 槽口高度为la/mm， 则另一端槽口高度为lb/mm. 槽口缺陷高度la小于1.5 mm时， 槽口缺陷几乎与断面平齐， 且游标卡尺测量不便， 读数趋于0， 故忽略不计. 试件编号t2.5-la1.94-lb0代表： 长度为420 mm， 直径168 mm， 壁厚2.5 mm， 一端槽口缺陷高度1.94 mm， 一端平整的圆钢管， 即单端缺陷圆钢管短柱. 试件的几何参数见表1.

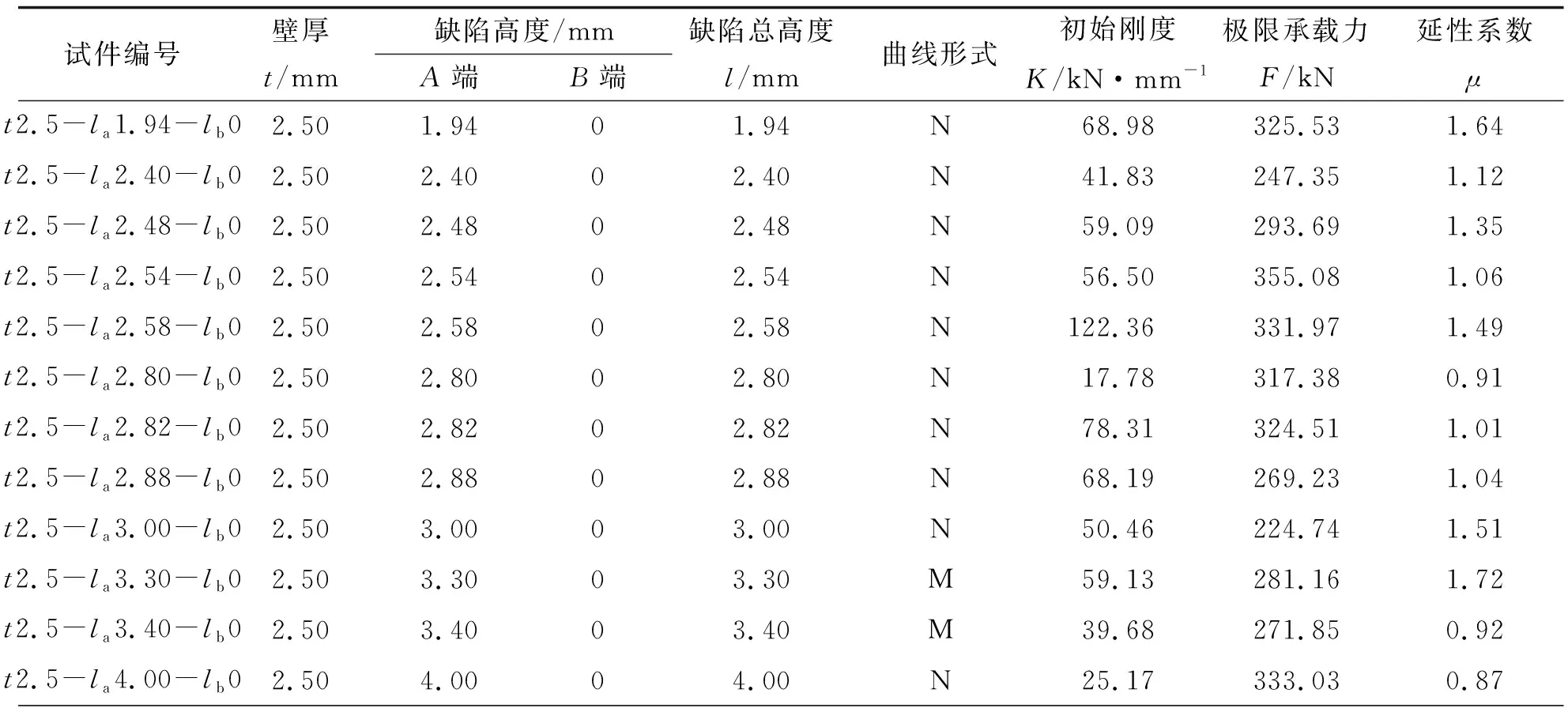
表1 试验数据一览表

续表1

1.2 试验加载设计

试验加载在福州大学土木工程学院一号实验馆进行， 加载、 荷载收集与记录采用5 000 kN压力试验机和2 000 kN万能试验机， 应变收集与记录采用DH3816数据采集系统. 在加载前， 对中圆钢管短柱， 并在圆钢管短柱的两端分别完全覆盖厚钢端板， 即厚钢端板边缘与圆钢管短柱边缘最小距离保持在2.5 cm以上， 确保荷载通过厚钢端板均匀布置在圆钢管短柱端部. 在正式加载初期， 采用荷载控制模式对弹性阶段进行加载. 随着荷载不断增加， 荷载-位移曲线呈线性上升， 当荷载-位移曲线出现略微弯曲或荷载达到60%无缺陷圆钢管短柱的极限承载力， 即刻调换至位移控制模式进行加载， 采集更多数据点的同时， 可以更好地稳定试验构件屈服后塑性阶段的卸载， 使得钢管在屈曲后有更明显的破坏现象. 在进行应变测试时， 加载初期采用单调分级静力加载， 每级加载停留1 min， 使用DH3816采集应变. 停机准则为： 在位移控制模式下， 随着试件位移的持续增加， 其荷载不断下降， 直至达到70%的极限荷载或压力试验机自动卸载， 即停止试验， 认为单个构件的试验结束.

1.3 试验测试方案

选取典型的4个试件进行应变测试， 应变布置如图1所示： 槽口缺陷处布置两个测点， 均贴三向应变片； 圆钢管短柱中部同一水平位置布置两个测点， 且两个测点与圆心的连线夹角为90°， 均贴双向应变片； 无槽口缺陷的端部布置一个测点并贴三向应变片. 编号t2.5-la0-lb0为无槽口缺陷圆钢管短柱， 编号t2.5-la6.76-lb0为一端两槽口(槽口H1和槽口H2)圆钢管短柱， 编号t2.5-la5.38-lb0、t2.5-la2.40-lb0均为一端槽口缺陷的钢管.

图1 应变片布置图Fig.1 Arrangement of strain gauges

2 试验结果及分析

2.1 破坏模式

2.5 mm壁厚的试件呈现两种破坏模式： 端部槽口缺陷处的凹陷屈曲(见图2(a))和端部槽口缺陷处的凸起屈曲(见图2(b)). 4.0 mm壁厚的试件全部产生端部槽口缺陷处的凸起屈曲的破坏现象， 并未发现有槽口缺陷处的凹陷屈曲的情况.

经过分析可知： 由于槽口缺陷的存在， 荷载最先作用在槽口缺陷处. 随着荷载的增加， 槽口缺陷处先发生局部屈曲(见图2(c))， 这种槽口缺陷的局部屈曲分为两种： 凹陷屈曲和凸起屈曲. 当局部屈曲变形达到一定程度， 即槽口缺陷高度降低为零， 圆钢管短柱全截面受压. 一部分发生凹陷屈曲的圆钢管短柱继续加载， 端部同一截面上的非槽口缺陷区域产生凸起屈曲， 同时钢管逐渐丧失最大承载能力， 直至全截面屈曲. 另一部分发生凸起屈曲的圆钢管短柱继续加载， 其凸起屈曲向同一截面上的非槽口缺陷区域延伸， 直至整个端部凸起屈曲， 钢管丧失最大承载能力， 即全截面屈曲.

(a) 凹陷屈曲

(b) 凸起屈曲

(c) 槽口缺陷处局部屈曲

2.2 荷载-位移曲线

由荷载-位移曲线(图3(a))可知：t4.0-la1.68-lb0、t4.0-la1.98-lb0的初始刚度与t4.0-la0-lb0无损试件的初始刚度近似相等， 可见在槽口缺陷高度小于0.5t时， 圆钢管短柱的初始刚度几乎无变化并且极限承载力近似相等. 当槽口缺陷高度大于0.5t时， 圆钢管短柱的初始刚度大幅减小， 且极限承载力降低. 槽口缺陷高度大于0.5t的圆钢管短柱初始刚度(见图3(b))仅仅是编号t4.0-la0-lb0无损试件初始刚度的4/10. 带槽口缺陷的圆钢管短柱荷载-位移曲线与无损试件荷载-位移曲线的形势保持一致， 且壁厚为4.0 mm的试件都呈现出凸起屈曲的破坏模式.

壁厚为2.5 mm的试件， 无论单端槽口缺陷(见图3(c)～(f))还是两端槽口缺陷(见图3(g)～(i))， 其初始刚度都大大减小， 带槽口缺陷的圆钢管短柱的初始刚度仅仅是编号t2.5-la0-lb0无损试件初始刚度的1/10. 其极限承载力大幅降低， 并且当槽口缺陷高度大于2t时(见图3(f))出现双峰曲线. 双峰曲线的出现， 恰好佐证了槽口缺陷对圆钢管短柱的影响： 当槽口缺陷高度la较小时， 不断加载的过程中， 槽口缺陷处先出现变形， 但不至于屈服. 当槽口缺陷高度变形至la=0， 此时全截面受压， 直至圆钢管短柱全截面屈服， 如图3(c)～(e)所示.

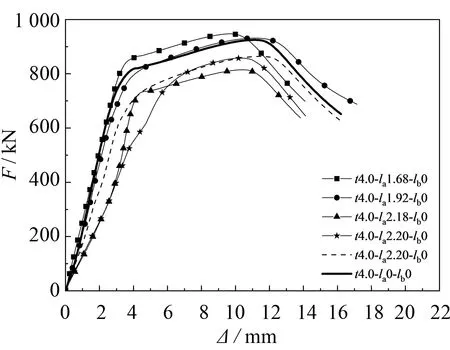
(a) t4.0-la1.68～2.20单端缺陷

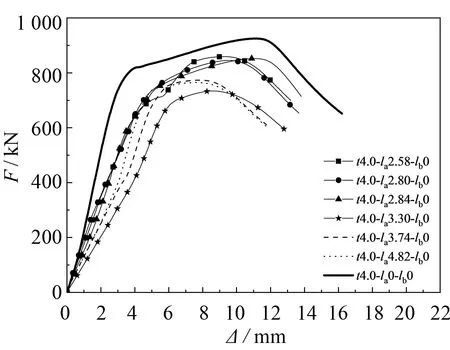
(b) t4.0-la2.58～4.82单端缺陷

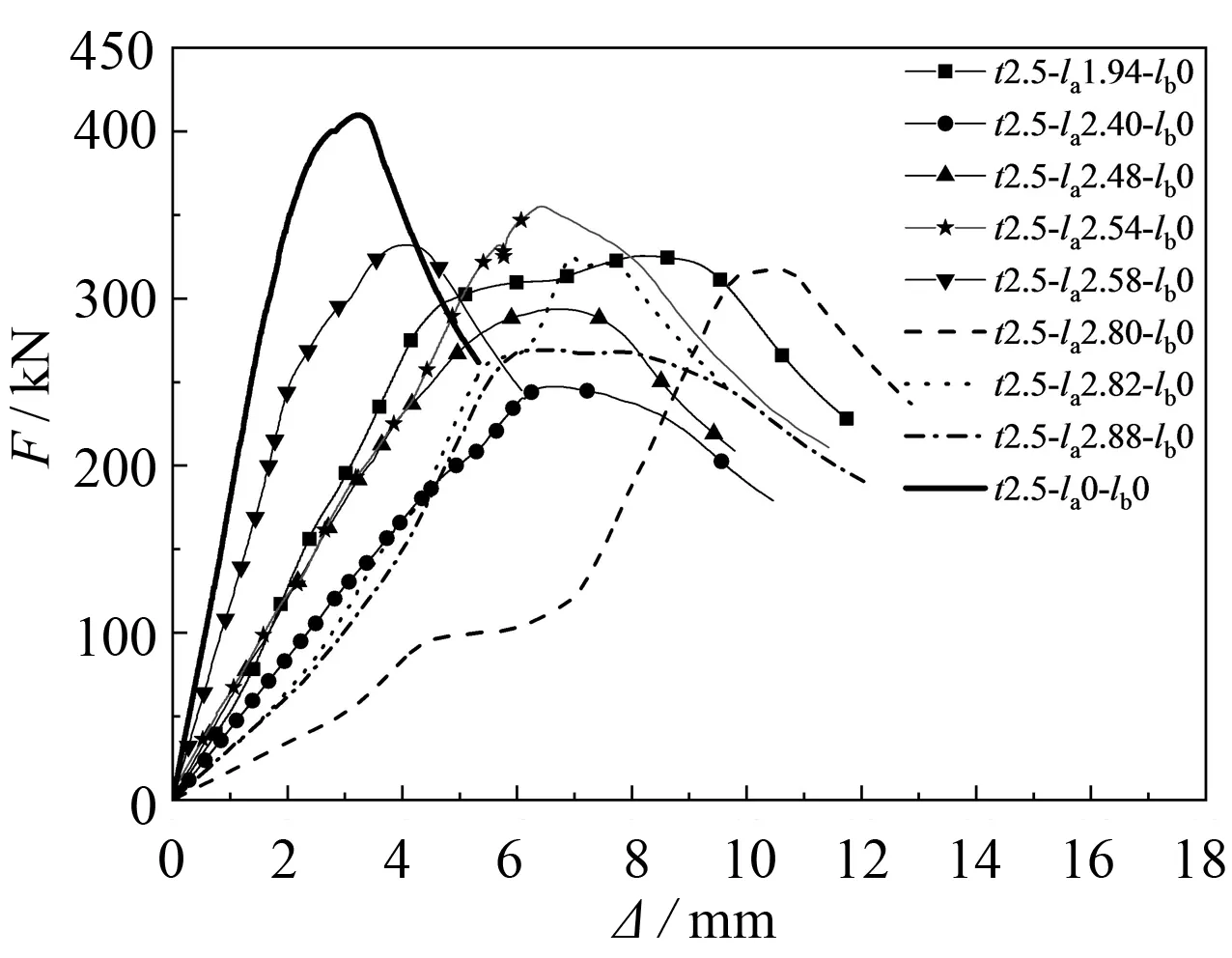
(c) t2.5-la1.94～2.88单端缺陷

(d) t2.5-la3.00～4.20单端缺陷

(e) t2.5-la4.30～4.96单端缺陷

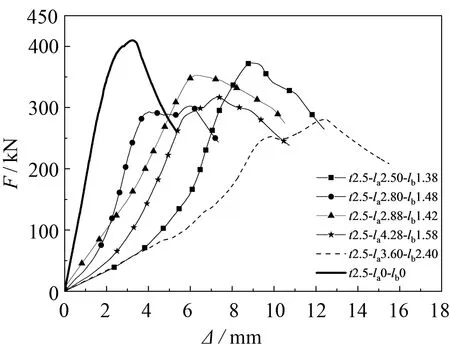
(g) t2.5-la+b3.88～6.00两端缺陷

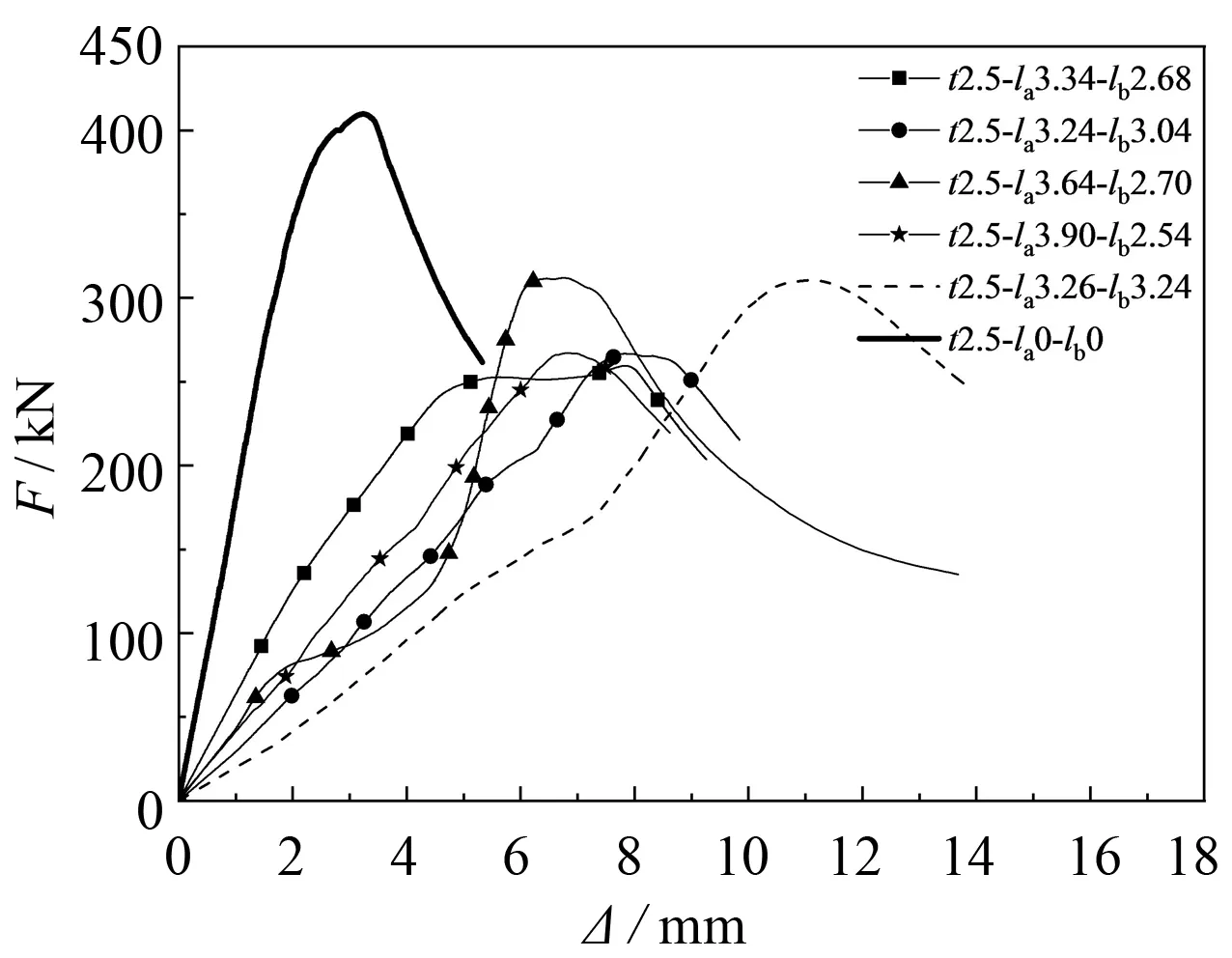
(h) t2.5-la+b6.02～6.50两端缺陷

(i) t2.5-la+b7.34～9.08两端缺陷

当槽口缺陷高度la>2t时， 不断加载的过程中， 槽口缺陷处未达到la=0就已经局部屈服， 出现第一个波峰. 试验压力机逐渐卸载， 随着位移的增加，la减小至0， 圆钢管短柱全截面受压， 从而试验压力机由卸载转为加载， 直至全截面屈服， 出现第二个波峰， 如图3(f)所示. 双峰曲线多存在于凹陷屈曲的破坏模式中， 试验过程中也存在槽口缺陷处发生凹陷屈曲的局部屈曲导致的试件丧失整体承载能力的情况， 即荷载加至第一个波峰后卸载时试验压力机自动卸载， 如t2.5-la3.00-lb0.

综上所述， 荷载-位移曲线分为两类： ① 与无损试件曲线形式大致相似的单峰曲线， 记为N； ② 由上升转为下降， 下降一定程度后再次上升， 直至最终下降的双峰曲线， 记为M. 曲线归纳具体见表1.

2.3 初始刚度-槽口缺陷高度曲线

通过对荷载-位移曲线弹性阶段的分析与计算， 得到试件弹性阶段的曲线斜率， 记为初始刚度K/kN·mm-1， 具体计算结果见表1.

初始刚度-槽口缺陷高度曲线如图4所示. 由图4(a)可知， 单端槽口缺陷的圆钢管短柱初始刚度相比无损试件的初始刚度有明显下降， 且在40～80 kN·mm-1之间波动. 由图4(b)可知， 双端槽口缺陷的圆钢管短柱初始刚度随着槽口缺陷高度的增加而减小， 曲线虽有波动， 但波幅比单端槽口缺陷的情况小很多; 此外波幅逐渐减小， 由20～50 kN·mm-1向35 kN·mm-1收敛. 由图4(c)可知， 槽口缺陷高度小于0.5t时， 试件初始刚度略有下降； 槽口缺陷高度达到0.5t～0.8t时， 试件初始刚度大幅下降； 在槽口缺陷大于0.8t时， 试件初始刚度趋于稳定.

综上所述， 槽口缺陷的存在会减小圆钢管短柱的初始刚度. 单端槽口缺陷的圆钢管短柱，t=2.5 mm试件初始刚度平均减小了67.28%，t=4.0 mm试件初始刚度平均减小了41.11%， 钢管短柱壁厚越大， 试件初始刚度减小的幅度越小. 两端槽口缺陷的圆钢管短柱， 随着槽口缺陷高度的增加初始刚度越小， 减小幅度逐渐收敛于35 kN·mm-1.

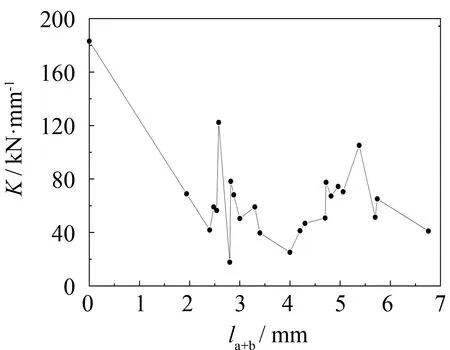
(a) t2.5单端缺陷

(b) t2.5两端缺陷

(c) t4.0单端缺陷

2.4 延性系数-槽口缺陷高度曲线

研究采用试件的极限位移Δu与屈服位移Δy的比值作为延性系数μ， 以探讨延性系数与槽口缺陷高度之间的关系.Δu取极限承载力对应的位移，Δy利用“割线刚度法”确定， 具体计算结果见表2.

延性系数-槽口缺陷高度曲线如图5所示. 由图5可知， 槽口缺陷的存在普遍减小了试件的延性系数.t=2.5 mm的圆钢管短柱延性系数下降率大约为30%(见图5(a)、 (b))，t=4.0 mm的圆钢管短柱延性系数随着槽口缺陷高度的增加而减小(见图5(c)). 试验过程中也存在延性系数提高的情况， 此现象多存在于双峰曲线中或偶有明显屈服平台的圆钢管短柱. 可见， 槽口缺陷的存在会小概率使圆钢管短柱轴压出现更为明显的屈服平台， 或形成双峰曲线， 导致延性系数提高.

由延性系数下降率可知， 槽口缺陷对圆钢管短柱延性的削弱作用在壁厚较大的试件中更为显著.

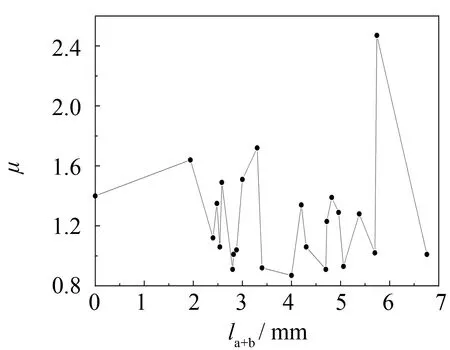
(a) t2.5单端缺陷

(b) t2.5两端缺陷

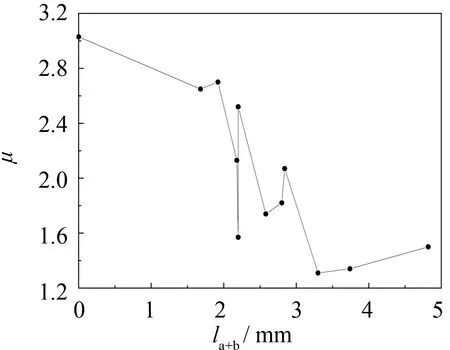
(c) t4.0单端缺陷

2.5 荷载-应变强度曲线

以编号t2.5-la0-lb0、t2.5-la6.76-lb0、t2.5-la5.38-lb0和t2.5-la2.40-lb0等4个典型的试件为例， 分析槽口缺陷区域应变强度的变化与规律， 探讨单端多槽口缺陷情况下取槽口缺陷高度最大值的合理性.

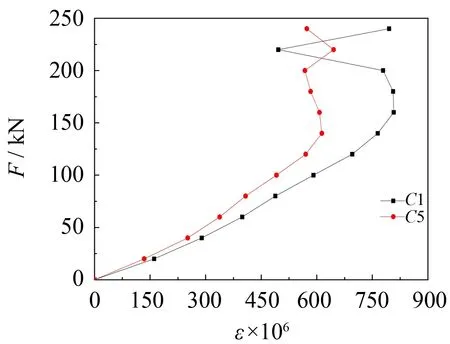
通过典型的4根圆钢管短柱在测点C1、C2处的荷载-应变强度曲线(见图6(a)、 (b))可知： 试件处于弹性阶段时， 应变强度随着槽口缺陷高度的增加而增加， 且t2.5-la0-lb0无损试件的曲线为凸曲线，t2.5-la6.76-lb0、t2.5-la5.38-lb0和t2.5-la2.40-lb0三根曲线均为凹曲线. 由此可知， 弹性阶段时， 应力主要集中在槽口缺陷处. 测点C4处的荷载-应变强度曲线均为凹曲线， 如图6(c)所示. 可见A端的槽口缺陷对圆钢管短柱B端的应变强度并无影响.

通过t2.5-la6.76-lb0试件(见图6(d))可知： 测点C1处的应变强度高于测点C6处的应变强度， 测点C5处的应变强度高度测点C7处的应变强度； 测点C1和C5的荷载-应变强度曲线在100 kN处发生突变， 测点C6和C7的曲线在120 kN处发生突变. 由此可知， 单端多槽口的情况下， 槽口缺陷高度最大值起着决定性作用， 其应变强度最大， 首先发生局部屈曲， 并向其他槽口缺陷处扩散至屈曲， 继而延伸至整个截面屈服.

通过t2.5-la5.38-lb0和t2.5-l02.40-lb0试件(见图6(e)、 (f))可知： 槽口缺陷上端应变强度比下端应变强度大. 可见， 槽口缺陷处的屈曲是由槽口缺陷上端向槽口缺陷下端发展.

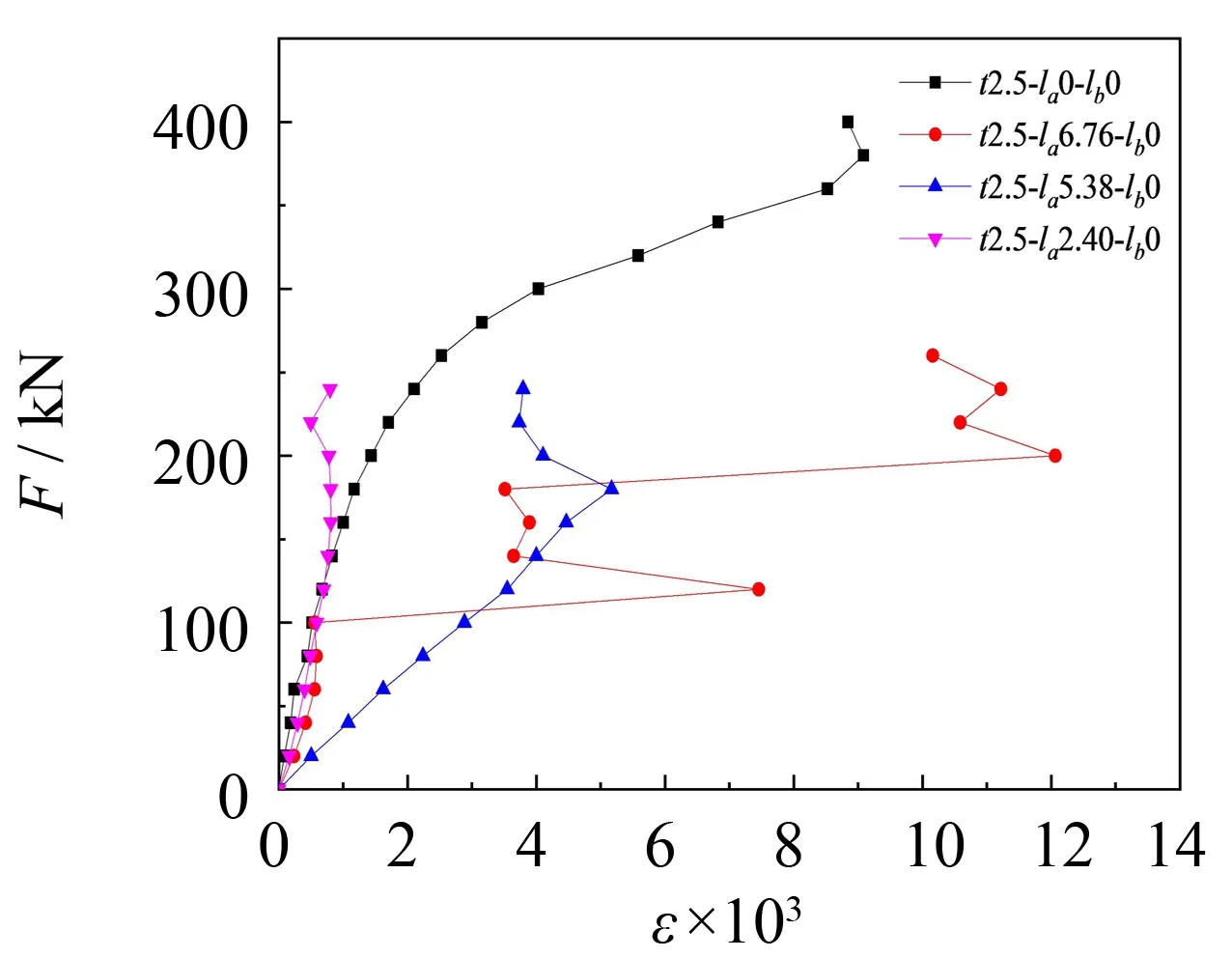
(a) C1测点

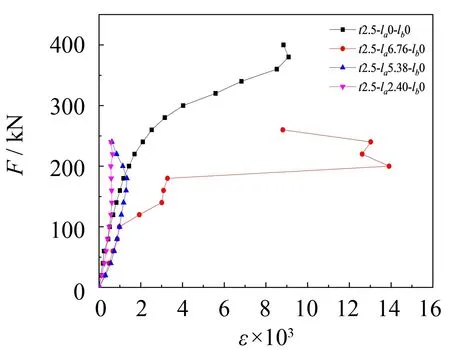
(b) C2测点

(d) t2.5-la6.76-lb0试件

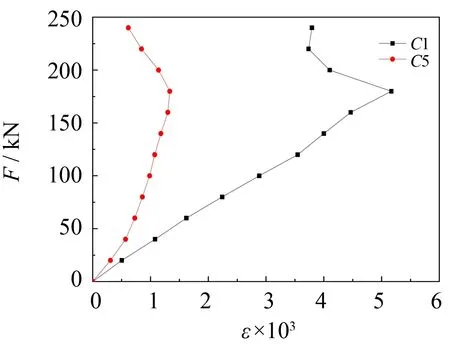
(e) t2.5-la5.38-lb0试件

(f) t2.5-la2.40-lb0试件

由图7荷载-应变曲线可知， 圆钢管短柱测点C2y的应变大于C2x，C3y的应变大于C3x. 故带槽口缺陷的圆钢管短柱腹中轴向应变大于环向应变， 在应变强度分布图中取测点C2y和C3y， 如图8所示. 由图8可知， 槽口缺陷上端应变强度最大， 槽口缺陷下端应变强度居第二， 带槽口缺陷的圆钢管短柱由槽口缺陷上端屈曲向下端屈曲发展.

综上所述， 应力集中在槽口缺陷高度最大值处， 使得槽口缺陷上端屈曲并向槽口缺陷下端发展. 与此同时， 槽口缺陷高度最大值处的局部屈曲向其他槽口缺陷处扩散. 所有槽口缺陷高度降低为零， 屈曲延伸至整个截面屈服.

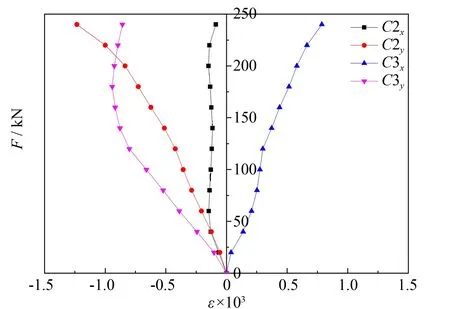
图7 t2.5-la5.38-lb0荷载-应变曲线Fig.7 Curves of load versus strain

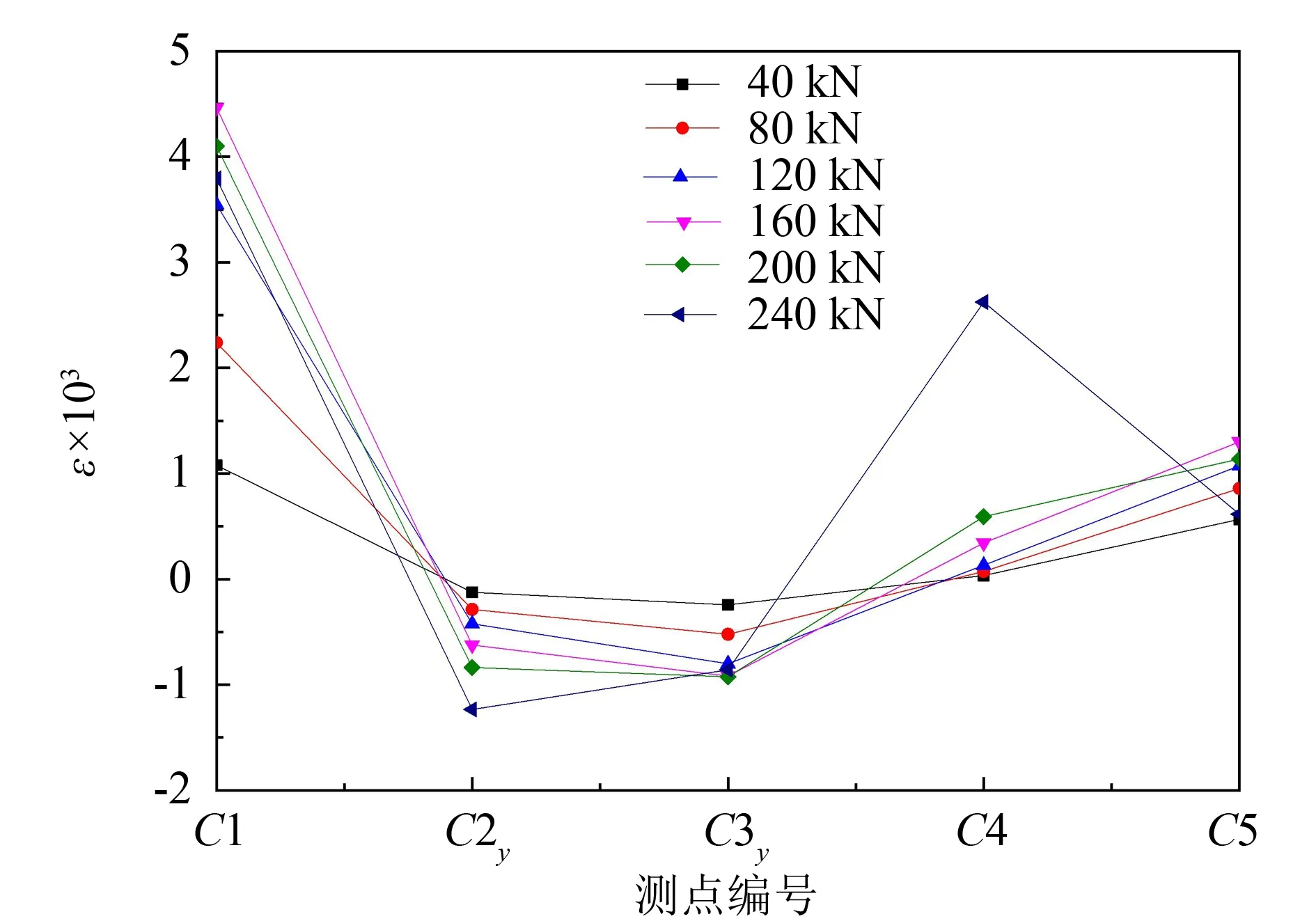
图8 t2.5-la5.38-lb0应变强度分布曲线Fig.8 Distribution of strain intensity curves

3 轴压承载力分析

对于壁厚t为4.0 mm的单端槽口缺陷圆钢管短柱(见图9(a))， 在槽口缺陷高度未达到0.5t时， 其极限承载力略有波动， 考虑到圆钢管短柱其他初始缺陷、 残余应力等因素的影响， 认为极限承载力无变化. 实际观测时， 当槽口缺陷高度未达到0.5t时， 圆钢管短柱并不会出现明显的局部屈服现象， 而是槽口缺陷被压平， 使得全截面轴心受压(偶有微微鼓曲， 但并未屈服). 当槽口缺陷高度达到0.5t～0.8t时， 圆钢管短柱极限承载力降低5%～10%. 当槽口缺陷高度达到0.8t及其以上时， 极限承载力降低10%～20%.

对于壁厚t为2.5 mm的单端槽口缺陷圆钢管短柱(见图9(b))， 并未发现明显的极限承载力与槽口高度之间的相关性， 可认为极限承载力降低20%～40%. 对比壁厚t为4.0 mm的圆钢管短柱发现， 圆钢管短柱的壁厚t较大时， 槽口缺陷高度的增加对极限承载力的影响较小， 而钢管壁厚t较小时， 槽口缺陷高度的增加对极限承载力的影响较大. 经过分析可知，t=4.0 mm时， 圆钢管短柱只有凸起屈服一种破坏模式， 而t=2.5 mm时， 圆钢管短柱会出现凹陷屈服和凸起屈服两种破坏模式. 但不论t为多少， 当槽口缺陷高度大于等于0.8t时， 圆钢管短柱的极限承载力至少下降20%. 并且受壁厚的影响， 壁厚t越小极限承载力的下降幅值越大， 下降程度达到但不限于20%，t=2.5 mm时， 下降幅值最大可达到40%.

对于壁厚t为2.5 mm的两端槽口缺陷圆钢管短柱(见图9(c))， 当槽口缺陷高度的平均值小于0.8t时， 极限承载力下降10%～20%. 当槽口缺陷高度的平均值达到0.8t及其以上， 极限承载力降低20%～40%.

由此可知

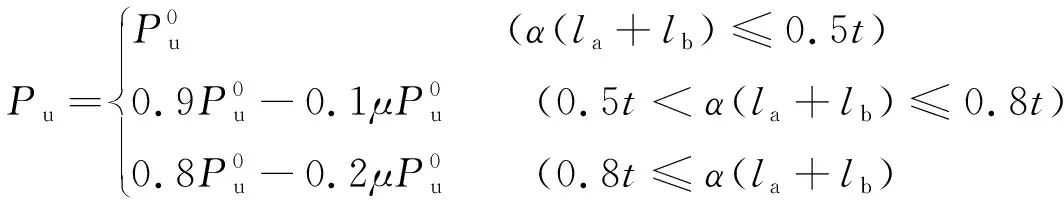
(1)

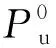
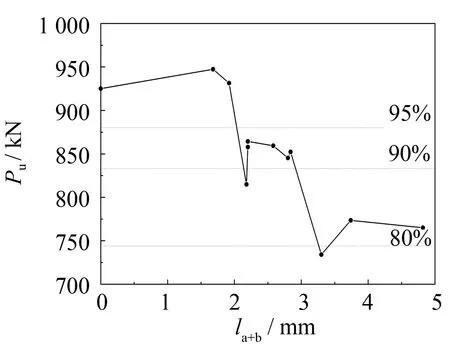
(a) t4.0 mm单端槽口缺陷

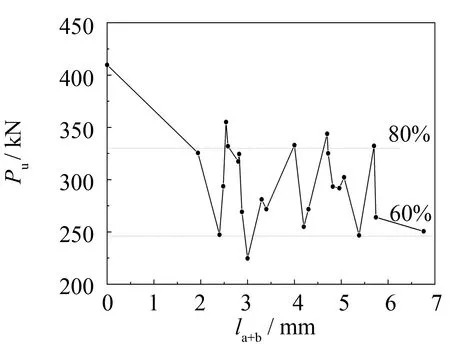
(b) t2.5 mm单端槽口缺陷

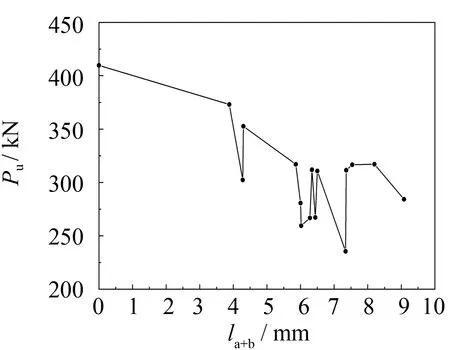
(c) t2.5 mm两端槽口缺陷

4 结论

通过对144根圆钢管短柱的筛选， 挑选出51根带槽口缺陷的圆钢管短柱， 对其进行静力承载性能测试. 试验结果及承载力分析可得如下5点结论.

1) 壁厚较大的带槽口缺陷的圆钢管短柱只有一种破坏形态, 即起屈曲， 荷载-位移曲线也只有单峰一种形式； 壁厚较小的带槽口缺陷的圆钢管短柱具有两种破坏形态， 即凸起屈曲和凹陷屈曲， 荷载-位移曲线也出现单峰曲线和双峰曲线两种形式.

2) 槽口缺陷的存在会减小圆钢管短柱的初始刚度， 且壁厚较小的圆钢管短柱初始刚度减小幅度大于壁厚较大的圆钢管短柱.

3) 槽口缺陷的存在普遍会减小圆钢管短柱的延性系数， 且壁厚较大的圆钢管短柱延性系数减小幅度大于壁厚较小的圆钢管短柱； 槽口缺陷的存在会小概率使得圆钢管短柱有更明显的屈服平台或直接形成双峰曲线， 从而使得试件的延性系数增大.

4) 带槽口缺陷的圆钢管短柱壁厚越小， 其极限承载力的下降幅值越大， 但极限承载力的下降峰值与壁厚无关.

5) 槽口缺陷高度小于0.5倍壁厚的试件， 其初始刚度、 延性系数和极限承载力在误差的允许范围内仅仅略有波动， 推荐可以继续使用. 槽口缺陷高度大于0.5倍壁厚且小于0.8倍壁厚的试件， 其初始刚度和延性系数有所减小， 极限承载力减小10%～20%； 槽口缺陷高度大于0.8倍壁厚的试件， 其初始刚度和延性系数大幅减小， 极限承载力减小20%～40%， 不推荐继续使用.