二自由度超声波电机惯性驱动研究
2018-06-19郭吉丰
王 剑 白 洋 郭吉丰
浙江大学电气工程学院,杭州,310027
0 引言
电机惯性冲击的驱动方法是压电驱动领域的一项新的尝试,它利用压电陶瓷的逆压电效应和惯性位移原理,将定子的静变形通过摩擦力作用,以惯性位移的形式传递运动[1],适用于高分辨率、大行程和小作用力的场合。国内外学者对惯性冲击式压电致动器的研究主要集中在精密位移平台、多自由度执行器和微型机器人等领域[2]。MORITA等[3]开发出一种基于多层压电结构的致动器,利用惯性冲击原理驱动,在锯齿波电压激励下,可实现空载转速27 r/min和堵转力矩0.56 N·m的输出。而后,MORITA等[4]又研制出相同原理的并联致动器结构,可将运动偏差控制在0~18.6 μm范围内。NISHIMURA等[5]研制出惯性冲击原理的直线超声波电机,该电机具备速度快和推力足的优点,可实现直线速度0.28 m/s和最大推力3.1N的输出。卢秋红等[6]设计出可实现圆周和直线运动的压电型惯性微驱动器,并建立了动力学模型,进一步可借鉴纳米摩擦学分析其动态特性。张宏壮等[7]利用压电双晶片作为驱动单元,提出一种惯性冲击式二自由度精密驱动器,选择了定频调幅的控制模式。刘俊标等[8]提出惯性冲击式压电微电机的改进型结构,可有效克服重心偏移,在电机动力学计算基础上,设计了基于模拟信号的匹配电源,具有稳定的运行效果。KANG等[9]采用方波和三角波信号分别作为惯性冲击方法的输入源,针对电机速度和力矩两个维度的输出作比对测试,证明了方波信号的激励效果优于三角波信号的激励效果。黄卫清等[10]设计了基于惯性冲击原理的三驱动足精密定位装置,可实现夹持负载纳米级的定位精度。
本文提出的改进型旋转-直线二自由度超声波电机属于多自由度电机的特殊分支[11],其构造机理和激励方式如下:倾斜布置在定子表面的单种压电陶瓷,既能激励定子的扭转振动,也能激励其纵向振动;采用基于惯性冲击原理的单相驱动电源即可实现旋转和直线两种运动。本文介绍了该电机的构造机理,阐述了惯性冲击方法的电机驱动原理,建立了电机的驱动数学模型,并对不同输入条件下的非对称方波激励进行算例分析。
1 构造机理
旋转-直线二自由度超声波电机的构造见图1,定子复合体(定子柱体)由金属弹性体和压电陶瓷组成:金属弹性体采用变截面结构,由圆柱过渡到正四棱柱,在正四棱柱的表面开定位槽黏接压电陶瓷,与定子轴线在空间上成一定的偏转角度,与金属弹性体共同构成压电激振体;转子环套接在圆柱表面,可灵活调节预紧力,实现旋转和直线二自由度运动。其中,压电陶瓷片沿厚度方向极化以充分利用压电应变系数d31;在压电陶瓷表面黏接柔性电路板,稳固连接单相激励电源。

图1 旋转-直线二自由度超声波电机构造图Fig.1 The sketch of rotary-linear 2-DOF ultrasonic motor
该电机最大的优势在于仅用单定子和单相电源即可实现二自由度运动。倾斜布置压电陶瓷片是为了充分激发扭振的振幅,倾斜角度的平衡设计可参考文献[12];单相电源可完全消除相位差对电机性能的影响,降低驱动电路的复杂度,与单相激励相匹配的驱动原理是近谐振点平稳惯性冲击方法(smooth impact drive method,SIDM)。根据有限元模态分析的结果可知,旋转运动由定子一阶扭振模态驱动,直线运动则由一阶纵振模态驱动。
2 驱动原理
鉴于旋转-直线二自由度超声波电机采用单定子结构,施加正弦波信号时,定子端面质点的伸缩位移/扭转角度是对称的,无法有效驱动转子输出宏观运动,因此电机惯性冲击的驱动方式需采用非对称方波信号激励,其频率、幅值和占空比均可调节,在纵向振动模式(直线运动)下驱动转子运动。建立定子和转子的受力分析,见图2,其中FN为转子受到的预压力,Ff为定子传递给转子环的摩擦力,ms、xs和mr、xr分别为定子和转子的质量与位移。静摩擦力Fs和动摩擦力Fk均遵循经典摩擦定理,其表达式如下:

式中,μs为静摩擦因数;μk为动摩擦因数。
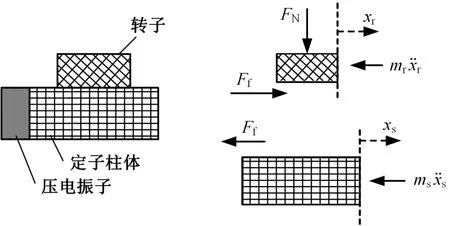
图2 定子和转子的受力分析Fig.2 Force analysis between the stator and rotor
当对电机施加非对称(占空比D≠50%)方波信号激励时,定子圆柱端面的质点位移为锯齿波,见图3。在单个周期A中,B段为定子端面位移的上升周期(定子伸长),C段为下降周期(定子回缩)。
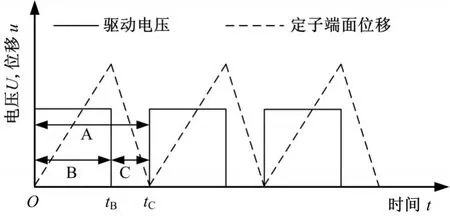
图3 非对称方波信号激励与定子端面位移关系示意图Fig.3 Relationship between asymmetric square wave excitation and linear displacement of stator
2.1 低频振动状态
当定子柱体处于低频振动时,在B区间内,定子、转子受到静摩擦力的限制,两者保持相对静止,其表达式如下:

定子柱体变形伸长,带动转子共同做平滑运动,位移为Δd,见图4。在tB时间点,转子的位移和速度可表示为

式中,τ为时间。
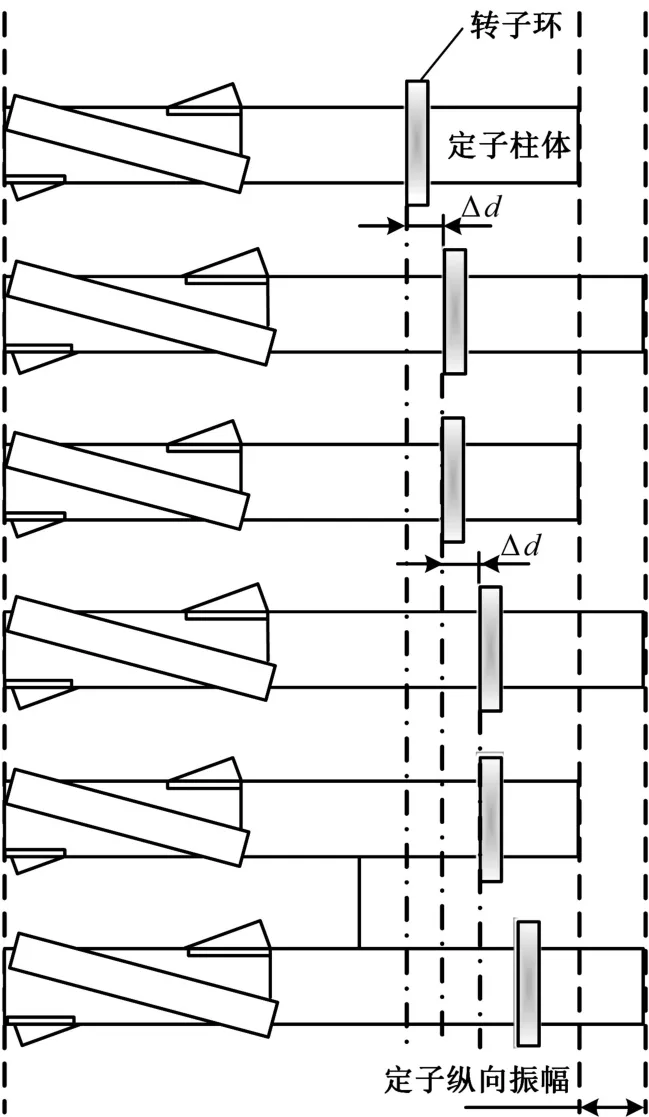
图4 转子位移示意图Fig.4 Schematic of rotor displacement
在C区间,方波信号下降到零电平,定子柱体随即回缩,转子加速度远小于定子加速度,得
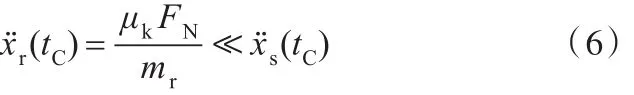
此时转子受到惯性影响,不随定子同步回缩,两者产生相对滑动,转子近似表现为静止状态。在tC时间点,转子的位移和速度可表示为

当方波信号又处于上升周期时,转子再随定子做平滑运动,位移为Δd,而后又保持近似静止的状态。微观上,转子保持随动→静止→随动的循环运动状态;宏观上,转子逐步积累为单一方向的直线运动。
2.2 高频振动状态
当定子柱体处于高频振动时,在B区间内,转子将突破静摩擦力的束缚,转为受动摩擦力驱使,定子和转子的运动方向一致,位移量不同。在tB时间点,转子的位移和速度可表示为

在C区间,方波信号下降到零电平,定子柱体随即回缩,定子加速度远大于转子加速度。转子受到惯性的影响,会继续保持在B区间的运动方向,定子和转子之间产生滑动,转子沿着定子柱体伸长的方向运动,转子的位移和速度可表示为
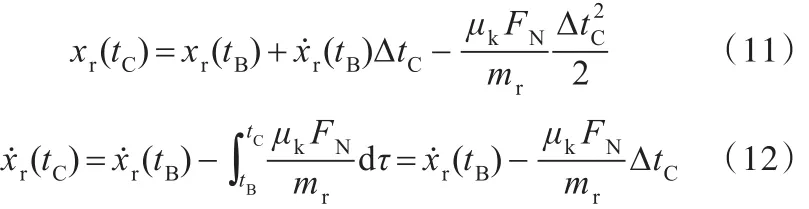
当方波信号再次处于上升周期时,转子在动摩擦力的作用下,再随定子做平滑运动,随后又保持滑动的状态。微观上,转子保持随动→滑动→随动的循环运动状态;宏观上,转子也逐步积累为单一方向的直线运动。
2.3 影响因素
实际上转子在C区间内停留的时间较短,所以无论低频或高频振动,转子的宏观运动都将保持单一方向的连续性。转子运动对摩擦因数、方波信号幅值和占空比等参数较为敏感。摩擦因数取值较大时,可确保转子在B区间保持随动,抑制转子在C区间的运动;但摩擦因数取值过大,可能导致转子在全周期与定子随动,电机无宏观位移输出;摩擦因数取值较小时,可促进转子在C区间的运动,抑制转子在B区间的随动;但摩擦因数取值过小,可能导致转子在全周期与定子相对滑动或保持静止,电机的输出不可控,因此,需选择合适的摩擦因数值来平衡提高电机的输出力能(包括输出力矩和速度)。方波信号幅值和占空比影响定子端面质点振动的形态:较大的电压幅值(非饱和)会增大定子端面锯齿波的位移幅值;占空比偏离50%的数值越大,会相应延长定子端面锯齿波的上升周期(或下降周期)。扭转振动模式(旋转运动)与纵向振动模式(直线运动)类似,此处不再展开。
3 驱动模型
为便于定子建模,先作近似和假设如下:①金属弹性体材质均匀,定子轴线始终垂直于定子柱体的截面;②压电陶瓷与金属棱柱黏接理想,忽略胶层对系统振动特性的影响,忽略压电陶瓷剪切变形的影响。
设定子柱体长度为 Lm,圆柱直径(棱柱边长)为Dm,压电陶瓷的长度、厚度、宽度和倾斜角度分别为 Lp、tp、wp和α,见图5。建模时将定子柱体等效为激励和传导两个部分:①激励部分包含金属棱柱及压电陶瓷,长度为l1;②传导部分为金属圆柱,长度为l2。l1和l2满足关系:l1=Lpcos α 和 l2=Lm-l1。

图5 定子驱动模型Fig.5 The drive model of the stator
定子纵向振动方程和扭转振动方程分别由瑞利理论和圣维南理论构建[12],在引入压电与金属复损耗系数[13]的基础上,可求得定子传导部分端面的n阶纵振模态的最大位移和n阶扭振模态的最大扭转角度:

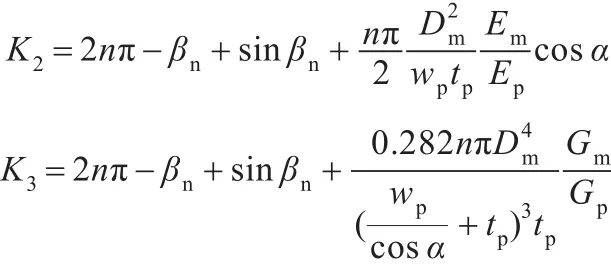
式中,Em、tan φ′和Gm分别为金属弹性体的弹性模量、损耗系数和剪切模量;Ep、η和Gp分别为压电陶瓷的弹性模量、损耗系数和剪切模量;γp为压电陶瓷的泊松比;U0为输入电压的幅值。
由上节可知,旋转-直线二自由度超声波电机的驱动原理为惯性冲击方式,频率选择在靠近谐振点,需输入非对称(D≠50%)方波信号,其表达式如下:

式中,T为方波周期;D为占空比。
根据Fourier变换,U(t,D)可分解为直流偏置量和多个高次正弦波,其表达式如下:

式中,ω为方波信号的角频率。
不考虑直流偏置量的情况下,将式(16)代入式(13)和式(14),可得到纵振和扭振模态下定子端面质点的位移形态。
在纵振模态下,当输入方波信号U(t,D)的激励时,定子端面的直线位移表示为
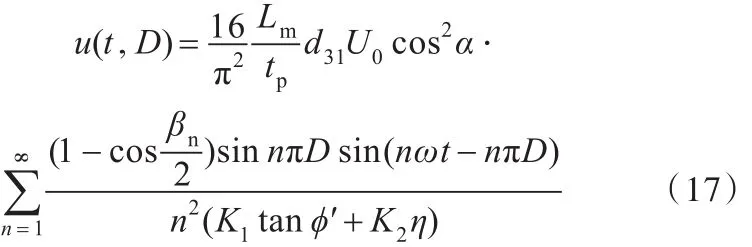
在扭振模态下,当输入方波信号U(t,D)的激励时,定子端面的旋转角度表示为

调节方波信号的频率ω,可切换电机直线和旋转两种运动模式。通过调节占空比D,可得到定子端面质点的直线位移/旋转角度的输出形态,当占空比D偏离50%时,该曲线形态接近锯齿波。
4 算例分析
计算所用的二自由度超声波电机的参数见表1。定子金属弹性体选用黄铜材料,压电陶瓷的型号为P-81。
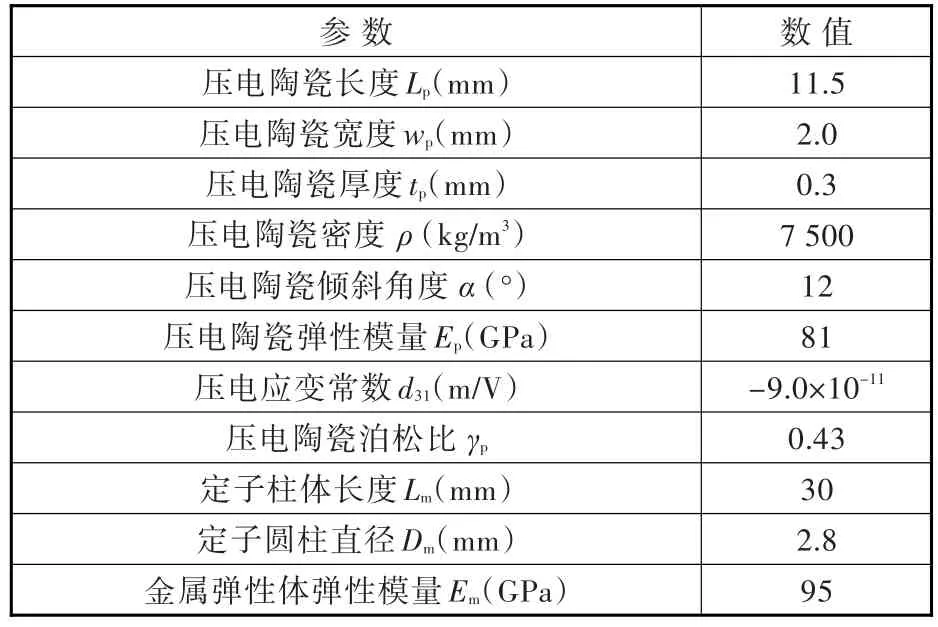
表1 旋转-直线二自由度超声波电机的参数Tab.1 The parameters of the rotary-linear 2-DOF ultrasonic motor
利用驱动模型对电机进行扫频分析,U0=50V,D=50%,f=25~60 kHz,结果见图 6。由图 6a可以看出,一阶扭振的谐振频率fT=29.9 kHz,最大旋转角度约为0.011°;由图6b可以看出,一阶纵振的谐振频率fL=52.6 kHz,最大直线位移约为0.32 μm。

图6 电机的振幅-频率特性Fig.6 Amplitude-frequency characteristics of the stator
对电机施加方波信号U0=50V,fL=53.6 kHz(n=1),占空比D=20%,33%,50%,66%和80%。利用式(17)得到定子一阶纵振的端面直线位移,见图7。由图7可以看出,当占空比D≠50%时,端面质点的直线位移呈锯齿波形态;占空比D距离50%越远,端面位移的最大幅值越小,对应的上升周期(或下降周期)越长。平衡考虑位移幅值和有效周期,并考量电机的力能输出,最终将方波的占空比选择在D=33%或66%,分别实现转子的前进和后退,因此输入非对称方波,可在定子端面输出符合条件的锯齿波,从而满足惯性冲击方法的驱动要求。

图7 不同占空比下的定子端面直线位移Fig.7 Linear displacement of the stator's end surface under different duty cycles
对电机输入方波信号fT=29.9 kHz(n=1),其他参数同纵振模态选用的参数。利用式(18)可得定子一阶扭振的端面质点旋转角度,见图8,可以看出,扭振模态的趋势与纵振模态的趋势一致。

图8 不同占空比下的定子端面旋转角度Fig.8 Rotation angle of the stator's end surface under different duty cycles
5 结论
(1)针对旋转-直线二自由度超声波电机,提出近谐振点惯性冲击的驱动方法。在定子、转子的接触与受力分析基础上,判定转子的宏观速度和位置,证明了电机在近谐振点处采用非对称方波激励,可将定子振动转换为转子的直线和旋转运动。
(2)提出该电机的驱动模型,定量分析了定子端面质点直线位移和旋转角度的输出波形。结果表明,在方波的占空比偏离50%后,定子端面的直向位移(或旋转角度)逐渐呈锯齿波形态,可有效驱动转子的直线和旋转运动。
(3)从压电陶瓷的倾斜排列和驱动方法入手,采用的单相惯性驱动方式不仅可简化驱动器结构,且完全消除了相位差对电机性能的影响,具有较高的应用价值。
[1] 赵淳生.超声电机技术与应用[M].北京:科学出版社,2007.ZHAO Chunsheng.Ultrasonic Motors Technologies and Applications[M].Beijing:Science Press,2007.
[2] 邢继春,许立忠.旋转惯性压电电机最优驱动方案分析[J].中国机械工程,2014,25(18):2451-2455.XING Jichun,XU Lizhong.Analysis of Optimal Driving of Rotary Inertial Piezoelectric Motor[J].China Mechanical Engineering,2014,25(18):2451-2455.
[3] MORITA T,YOSHIDA R,OKAMOTO Y,et al.A Smooth Impact Rotation Motor Using a Multi-layered Torsional Piezoelectric Actuator[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,1999,46(6):1439-1445.
[4] MORITA T,YOSHIDA R,OKAMOTO Y,et al.Three DOF Parallel Link Mechanism Utilizing Smooth Impact Drive Mechanism[J].Precision Engineering,2002,26(3):289-295.
[5] NISHIMURA T,HOSAKA H,MORITA T.Resonanttype Smooth Impact Drive Mechanism(SIDM)Actuator Using a Bolt-clamped Langevin Transducer[J].Ultrasonics,2012,52(1):75-80.
[6] 卢秋红,高志军,颜国正,等.压电型惯性微驱动器研究[J].压电与声光,2004,26(2):112-115.LU Qiuhong,GAO Zhijun,YAN Guozheng,et al.The Study on Miniature Inertial Piezo-actuators[J].Piezoelectric&Acoustooptics,2004,26(2):112-115.
[7] 张宏壮,程光明,曾平,等.压电双晶片型2自由度精密驱动器的动态特性[J].机械工程学报,2007,43(2):87-91.ZHANGHongzhuang,CHENGGuangming,ZENG Ping,et al.Dynamic Characteristics of 2-DOF Precision Positioning Device Utilizing Impact Force of End-loaded Piezoelectric CantileverBimorphs[J].Journal of Mechanical Engineering,2007,43(2):87-91.
[8] 姜楠,刘俊标,方光荣,等.惯性冲击式压电微电机的研究[J].压电与声光,2007,29(2):187-189.JIANG Nan,LIU Junbiao,FANG Guangrong,et al.Research on Impact Drive Mechanism Piezoelectric Micro-motor[J].Piezoelectric&Acoustooptics,2007,29(2):187-189.
[9] KANG C Y,YOO K H,KO H P,et al.Analysis of Driving Mechanism for Tiny Piezoelectric Linear Motor[J].Journal of Electroceramics,2006,17(214):609-612.
[10] 周昇,黄卫清,朱华,等.惯性冲击式压电精密定位装置的设计[J].机械科学与技术,2016,35(7):992-997.ZHOU Sheng,HUANG Weiqing,ZHU Hua,et al.Design of Piezoelectric Precision Positioning Device based on Inertial Impaction[J].Mechanical Science and Technology for Aerospace Engineering,2016,35(7):992-997.
[11] TUNCDEMIR S,URAL S O,KOC B,et al.Design of Translation Rotary Ultrasonic Motor with Slanted Piezoelectric Ceramics[J].Japanese Journal of Applied Physics,2011,50:027301.
[12] 王剑,白洋,郭吉丰.旋转-直线型两自由度超声波电机建模与设计[J].电工技术学报,2013,28(11):48-53.WANG Jian,BAI Yang,GUO Jifeng.Modeling and Optimal Design of the Rotary-linear Type Two-degree-of-freedom Ultrasonic Motor[J].Transactions of China Electrotechnical Society,2013,28(11):48-53.
[13] BAI Y,TUNCDEMIR S,GUO J F,et al.Analysis of Longitudinal and Torsional Resonance Vibrations of a Piezoelectrically Excited Bar by Introducing Piezoelectric Loss Coefficients[J].Journal of Intelligent Material Systems and Structures,2012,23(4):453-462.
