基于遗传算法的公交车调度问题
2018-06-18徐浩吴海霞李婷婷白雪
徐浩 吴海霞 李婷婷 白雪
石家庄铁道大学 河北省石家庄市 050000
1 问题重述
非线性规划模型。
本文以2001年全国大学生数学建模竞赛B题为例。
公共交通对于城市运作具有重大意义,已知某大城市有一条公交线路,该线路上行有14站,下行有13站。该线路上的大客车为同一型号,标准载客量为100人,客车平均速度为20公里/小时。要求,乘客候车时间不能超过10分钟,早高峰时不能超过5分钟,车辆的满载率不能超过120%,一般也不低于50%。
为该线路设计一个公交车调度方案,包括两个起点站的发车时刻表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘客和公交公司双方的利益。
2 问题分析
题目要求设计调度方案,则需要求出发车间隔,可以设置发车间隔为自变量,利用候车人数、公交车辆数等因素,推导出满载率、全天发车次数、所需公交车辆数。同时综合考虑公交车公司和乘客的利益,引入公交车行驶成本和乘客等待成本两个概念。对于公交车公司来说,发车时间间隔越长,全天发车次数越少,需要的公交车越少,成本越低;对于乘客来说,发车间隔越短,乘客等待时间越短,成本越低。因此公交车公司和乘客的利益是对立的,需要考虑在不同的程度下照顾公交公司和乘客的利益,所以引入权重概念,将多目标转化为单目标,建立
3 问题假设
(1)假设每个时间段内乘客到达数服从均匀分布;(2)假设汽车一直以平均速度行驶,不受外界因素影响;(3)假设乘客上下车时间非常短,可以忽略不计;(4)假设公交车到达终点站返回时可以载客。
4 模型的建立
假设第i个时间段发车间隔为ti,时长为Ti,第i个时间段第j个站上车人数为uij,下车人数为vij,(i=1,2,…,m,j=1,2,…,n)。标准载客人数为P人,路线总长为L千米,公交车平均行驶速度为V千米/小时,公交车每公里运行成本为C1元/(辆·千米),乘客每分钟等待成本为C2元/(人·分钟)。
则第i个时间段发车数

第i个时间段第j个站平均每辆车人数

第i个时间段第j个站和第j+1个站之间的车的满载率
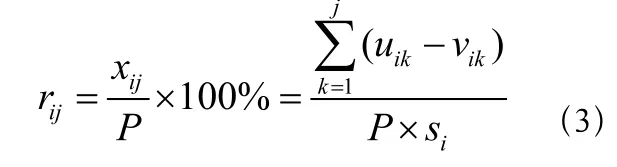
全天平均满载率

一个工作日发车总数
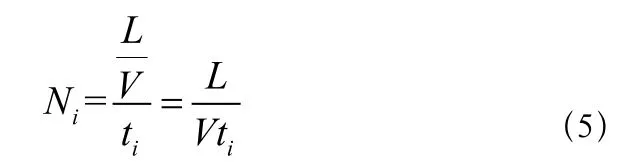
第i个时间段线路上单向车辆数
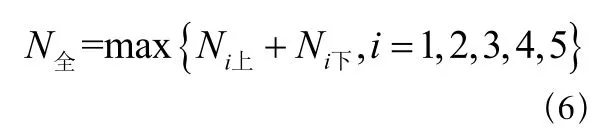
全天所需公交车辆数

公交车公司的目标是一个工作日内所有公交车运行成本最低,表示为
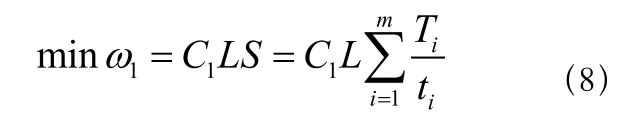
乘客的目标是一个工作日内所有乘客等待成本最低,表示为

发车间隔时要求高峰期不要超过5分钟,非高峰期不要超过10分钟,得到发车间隔约束条件为
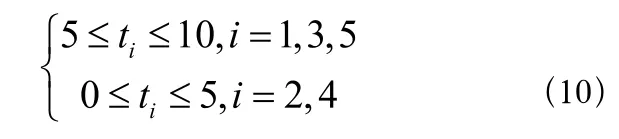
公交车可以载客人数较少,但绝对不能超载,由此得到满载率约束条件为

引入权重,将多目标规划转化为单目标规划,得到综合考虑公交车公司和乘客双方总成本的规划模型
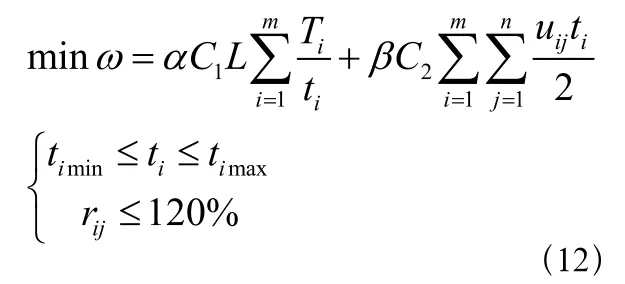
其中α、β为权重系数,且α+β=1。
5 模型的求解
该问题是一个复杂的规划问题,用经典的优化方法难以求解,可以利用遗传算法进行求解。
5.1 参数取定
对于编码方式,本文采用二进制编码;对于初始种群,可以通过随机生成的方法产生初始种群,本文设置种群规模为20;对于适应度函数,本文设定适应度越小适应性越强,将目标函数作为适应度函数;对于选择操作,本文选用轮盘赌法;对于交叉操作,本文采用单点交叉的方式,交叉概率取0.8;对于变异操作,本文采用基本位变异,变异概率设置为0.01;设置搜索终止的条件为迭代次数达到100次。
根据所给数据,上行方向行驶距离14.58千米,下行方向14.61千米。公交车每公里运行燃料花费为2~3元,考虑到其他花费,设公交车每公里运行成本C1=10元。乘客每分钟等待的成本即乘客用等待的时间所能创造的价值,以北京为例,通过访问北京市统计局官网可知,2016年北京居民人均可支配收入为52530元,第五次全国人口普查显示,北京市人均每周工作5.9天,则北京居民一年有365-10-52×1.1=297.8个工作日。按每天工作8小时记,则一个乘客每分钟等待成本
5.2 结果的分析与检验
取权重系数α=0.6,β=0.4,可以求得最优发车间隔,根据式(1)计算可得各时间段发车数,得到简化发车时刻及发车数如表1所示。
经过计算可得一个工作日总发车数S为524辆,全天平均满载率R为76.612%。
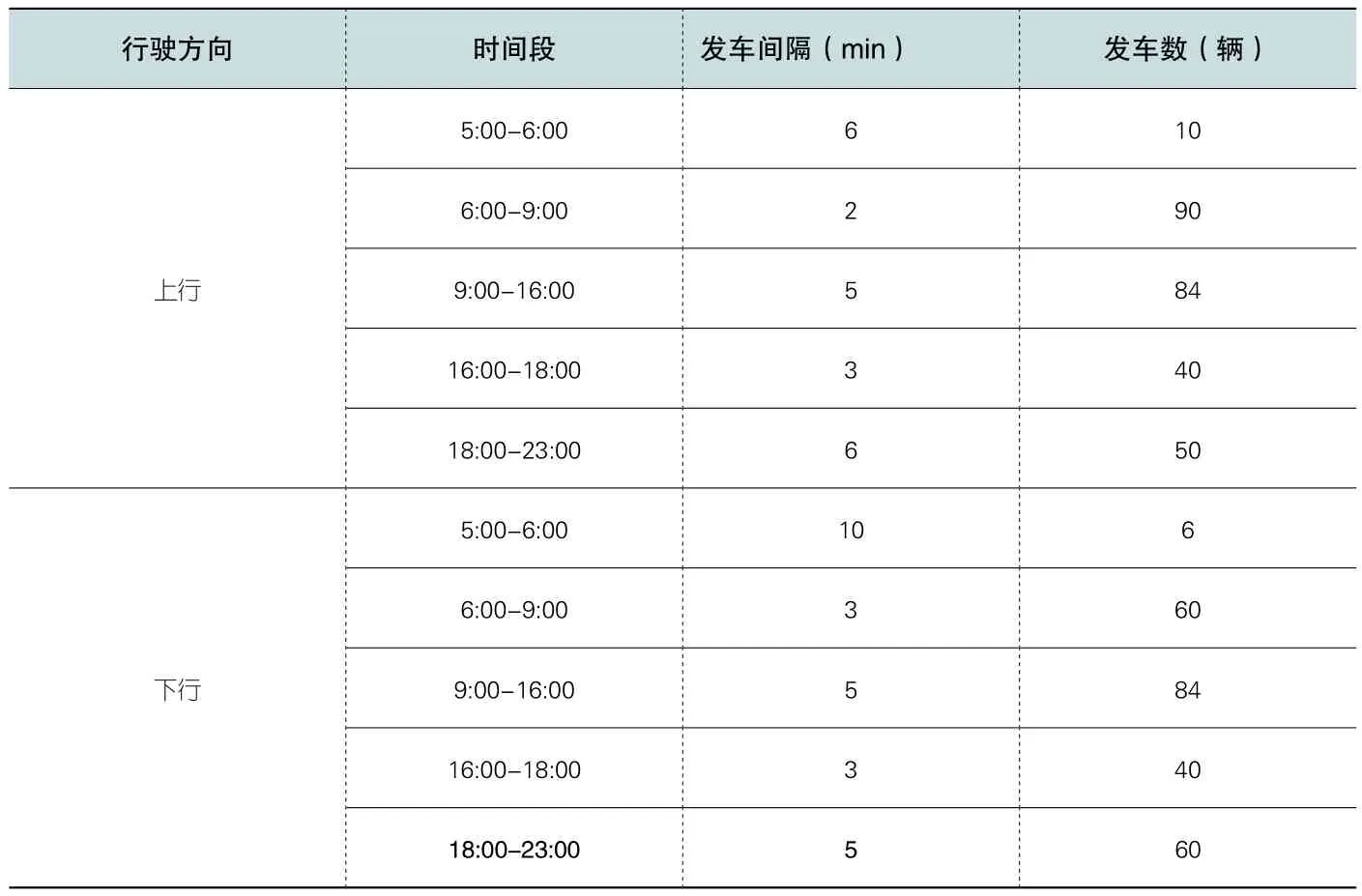
表1 简化发车时刻表
根据式(5)计算可得各个时间段线路中上下行车辆数目如表2所示。
由上表可以看出,早高峰6:00-9:00时间段所需公交车数量最多,为37辆,全天所需公交车数目不会超过早高峰所需车辆数目,所以全天所需公交车辆数为37辆。
6 模型的评价与推广
该模型从实际出发,综合考虑了公交车公司和乘客双方的利益,建立了总成本最低的非线性规划模型,成本系数的设定结合了生活实际,有较高的可信度。且利用遗传算法对复杂优化问题进行求解,大大缩短了求解时间。同时模型具有较高的适用性,对于不同的城市不同的公交路线,只需要将相关系数更正,将观测数据代入模型,即可得到较为合理的发车安排。
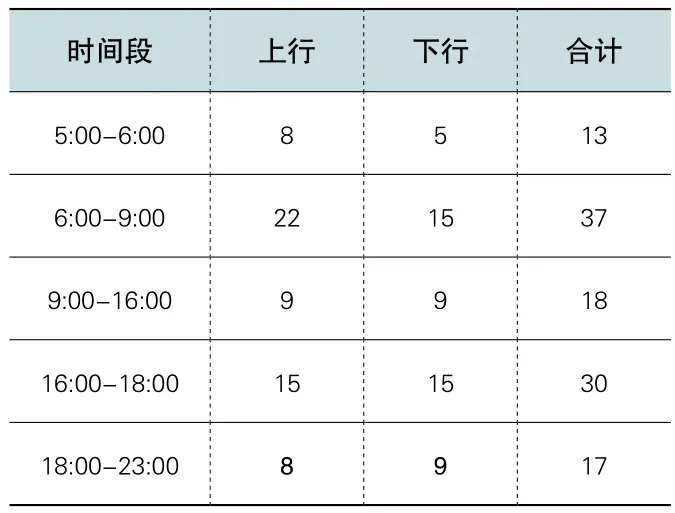
表2 线路中上下行车辆数目表
