空间半参数变系数部分线性分位数回归中的B-样条估计法

唐庆国，晋 鹏

(南京理工大学 经济管理学院，江苏 南京 210007)

一、引 言

空间数据，顾名思义，指的是与空间位置相关的观测数据。空间数据广泛存在于环境科学、传染病学、气象学、地理科学、生物医学、政治学及经济学等自然科学和社会科学的众多领域。例如：环境科学中各种污染数据(空气污染、水污染、土壤污染等)，传染病学中各种数据(患病人数、传播速度等)，气象学中的各种气象数据(风速、温度、湿度、气压等)，地理科学中的各种地理信息数据，遥感监测数据，医学科学中的影像数据，经济学中房地产交易量及价格监测数据等。空间数据的统计分析不仅有着极其广泛的应用范围和重大的实用价值，而且已经广泛应用于这些领域中。通常收集到的数据呈不规则分布，但随着计算机技术的快速发展和广泛应用，在密集的规则格点上测量和收集数据变得越来越普遍。Cressie列举了空间数据和模型的大量应用例子[1]1-26。近年来，空间数据非参数估计方面的研究有了很大的发展，Hallin等推导了空间回归局部线性估计量的渐近正态性[2]；Gao等开发了半参数空间回归局部线性核估计量的渐近性质[3]；Lin等推导了空间非参数回归局部线性M-估计量的渐近性质[4]；Lu等研究了函数系数空间分位数回归的估计问题[5]；王康宁和林路研究了空间非参数回归的变量选择问题[6]。此外，周少甫和白羽研究了空间面板杜宾模型的Bootstrap Wald-COMPAC检验问题[7]；方丽婷研究了空间滞后面板平滑转换模型的估计问题[8]。

假定有在格点上的空间数据{(Yij,Xij,Zij,Uij)：1≤i≤m;1≤j≤n}，此处Yij和Uij取值于R，Xij取值于Rd1，Zij取值于Rd2，它们定义于某个概率空间(Ω,F,P)上。应用中经常会碰到空间回归问题，相依变量Yij与自变量Uij，Xij和Zij之间存在着复杂的空间相依关系。对这类问题通常的做法是假定Yij的条件期望存在，以便定义条件期望函数η(x,z,u)=E(Yij|Xij=x,Zij=z,Uij=u)并对其做相关的统计推断。正如许多文献中所提到的，当d1+d2+1>3时，由于“维数祸根”，空间回归函数不能较好地被估计。本文考虑空间分位数回归函数，并且试图用如下形式的变系数部分线性函数：

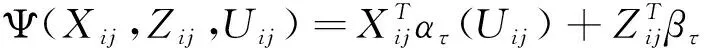
(1)

用式(1)来逼近空间分位数回归函数，即在以上变系数部分线性函数集{Ψ(Xij,Zij,Uij)}中选择一函数使Eρτ(Yij-Ψ(Xij,Zij,Uij))达到最小，此处ρτ(t)=t(τ-I(t<0)),0<τ<1为τ分位数损失函数，βτ=(βτ1，βτ2，…，βτ d2)T是一个d2维未知参数向量，而ατ(u)=(ατ1(u)，ατ2(u)，…，ατ d1(u))T是d1维未知系数函数向量。

迄今为止，已有不少人研究过变系数部分线性模型并已开发出不少新的理论成果，Zhang等开发了一种局部多项式估计法用以估计模型中的线性和非参数部分[9]；Fan 和 Huang 研究了基于剖面最小平方估计的广义似然比检验[10]；Wang等研究了纵向数据变系数部分线性模型的分位数估计[11]；Kai等开发了变系数部分线性模型新的估计和变量选择方法[12]。同均值回归相比，分位数回归具有以下几方面的优势：第一，给定一列分位数并对其中的每一个分位数做分位数回归比单纯做均值回归能更多、更好地认识和理解数据；第二，分位数拟合可用于构建预测区间；第三，中位数回归作为分位数回归中的一种特例能提供比均值回归更稳健的估计。作者使用两步估计法估计模型(1)中的未知参数和函数，推导了未知参数估计量的渐近分布并建立了未知函数估计量在内点及边界点的渐近分布[13]。本文开发了一种一步估计法用以估计模型(1)中的未知参数和函数，利用B-样条函数，所有未知参数和函数的估计量由一次极小化得到。由于只需要一次极小化算法，同两步法相比，一步法所需的计算量大为减少。我们推导了未知参数估计量的渐近分布，并建立了未知函数估计量的收敛速度。

二、估计方法

假定有观测数据(Yij,Xij,Zij,Uij),1≤i≤m;1≤j≤n，总的样本容量为N=m×n。不失一般性，假定0≤u≤1。

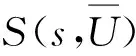
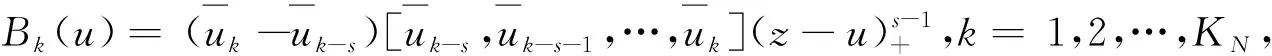
(2)

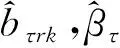
(3)

为了执行上面的估计程序，必需先确定光滑参数KN的值。KN的值可由信息准则BIC来选取，BIC作为KN的函数由下式定义：

使BIC达到最小的KN即为我们要选取的。

三、估计量的渐近性质

B(S)=B((Yij,Xij,Zij,Uij)∶(i,j)∈S)

和

B(S′)=B((Yij,Xij,Zij,Uij)∶(i,j)∈S′)为两个地址(i,j)分别属于S和S′的随机向量(Yij,Xij,Zij,Uij)所生成的σ域。令d(S,S′)为S与S′之间的欧氏距离，假定{(Yij,Xij,Zij,Uij)}满足以下定义的混合条件：存在一函数φ(t)，当t→时，φ(t)↓0，并且当S,S′⊂Z2时，有：

α(B(S),B(S′))

=sup{|P(AB)-P(A)P(B)|，A∈B(S)，

B∈B(S′)}≤φ(Card(S)，Card(S′))φ(d(S,S′))

(4)

此处Card(S)表示集合S中的元素个数，φ为一关于每一个分量非减的对称正函数。如果存在某个常数C使得φ(,)≤C，{(Yij,Xij,Zij,Uij)}称为α混合(或强混合)。在混合性条件中，α混合相依性是为建立估计量的渐近性质所需的较弱的条件。令为ρτ的导数。下面列出推导估计量的渐近性质所需的条件。

假设1 随机场{(Yij,Xij,Zij,Uij):(i,j) ∈Z2}是严平稳的，φ(n1,n2)≤min(n1,n2)且存在一常数ζ>0使得φ(t)=O(e-ζ t)。对于Z2中的(i,j)和(i′，j′)，随机变量Uij和Ui′j′有联合密度fij,i′j′，且对所有的(i,j)，(i′,j′)∈Z2及所有的u,v∈[0,1]，有|fij,i′j′(u,v)-f(u)f(v)|≤C0，此处C0为一常数，f为关于Uij的边缘密度，且f在[0,1]上连续且大于零。

假设2 对r=1，2，…，d1，ατr(u)∈Cs[0，1]这里的Cs[0,1]表示所有s次连续可微函数组成的函数空间。

假设4 min{m,n}→∞，KN=O(N1/(2s+1))，(KNlogN)3/m→0且(KNlogN)3/m→0。

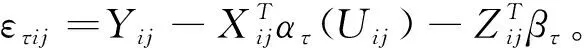
假设7 存在两个正整数值向量序列Pm,n=(p1,p2)∈Z2和qm,n=(q,q)∈Z2满足：q→，q/p1→0，q/p2→0，m/p1→，n/p2→，并且

令Π为所有如下函数组成的函数集合：

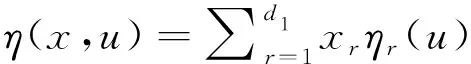
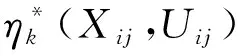
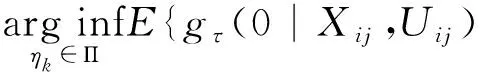
[Zijk-ηk(Xij,Uij)]2}

定理1 假定假设1～7成立，并且Aτ和Γτ有限且可逆。则有

(5)

证明：利用与文献[13]中定理1的证明相类似的方法可完成定理1的证明。

下面的定理2给出了未知函数ατr(u)的估计量的收敛速度。

定理2 假定假设1～7成立。则有：

(6)

r=1，2，…，d1

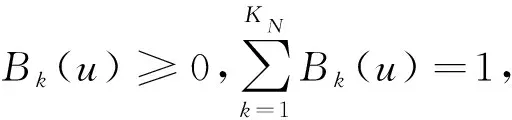
(7)

这里的C5和C6是两个正常数。根据假设2，利用Schumaker中的推论6.21[14]227，存在正常数C7使得：

(8)

(9)

令

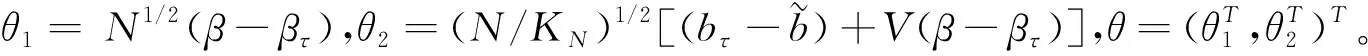
此处C8为一正常数。这就完成了定理2的证明。

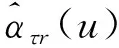
四、模 拟

Yij=Xij1ατ1(Uij)+Xij2ατ2(Uij)+Zij1β1+

Zij2β2+ετij

(10)

其中β1=1，β2=2，ατ1(u)=0.8eu/2+0.5e-u/2，

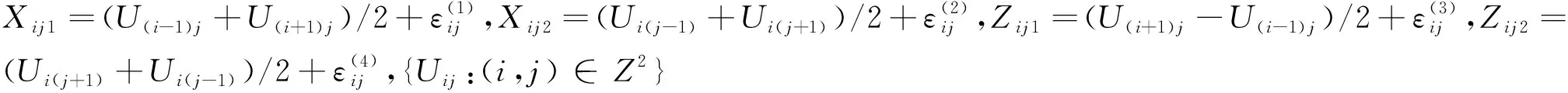
来自以上模型的模拟数据在一个有m×n个地址的长方形区域内产生，具体地说，在格点区域{(i,j):76≤i≤75+m,76 ≤j≤75+n}中产生。本文中，我们取m=10,n=20。每个样本按Hallin等提供的方法迭代产生[2]，300个空间样本数据独立地被产生。对每个样本数据，ατr(u),r=1,2的B-样条估计量由等分节点三次样条来计算。在表1的结果中，光滑参数KN由BIC准则选取。

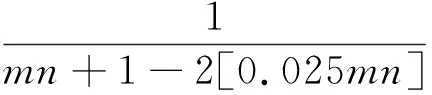
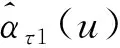
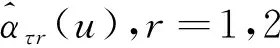
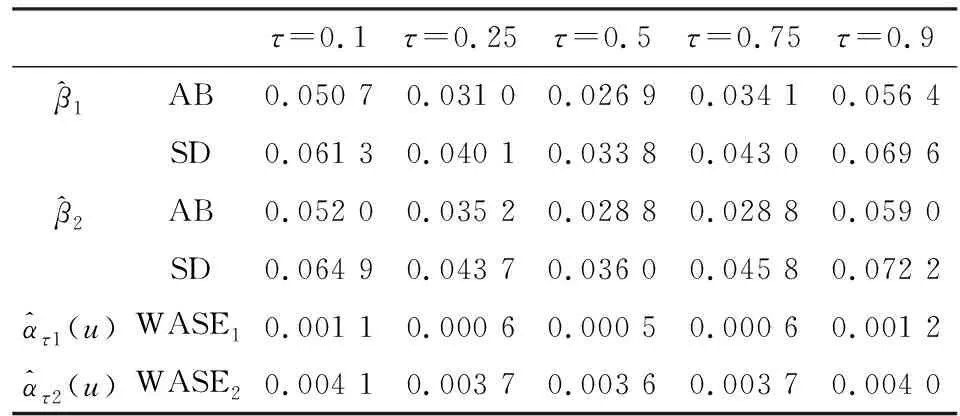
表1 300次模拟得到的有关AB、SD以及WASEr的结果

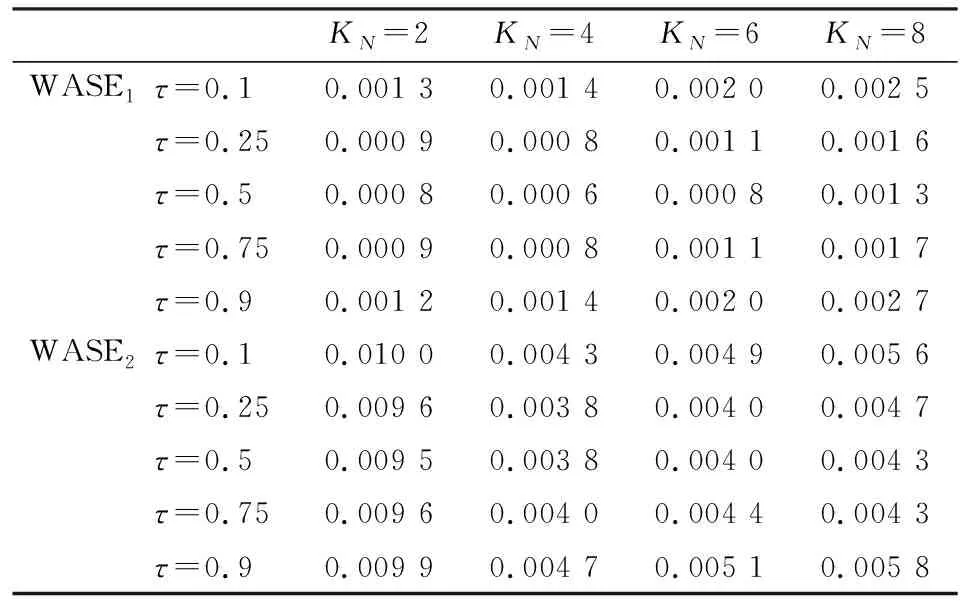
表2 WASEr，r=1，2随KN的变化情况

五、结 论

本文利用B-样条函数提出了一种一步估计法用以估计空间半参数变系数部分线性分位数回归中的未知参数和函数，所有未知参数和函数的估计量由一次极小化得到。我们推导了未知参数估计量的渐近分布并建立了未知系数函数估计量的收敛速度。从模拟结果看，本文提出的一步估计法要优于文献[13]中的两步法，而一步法的运行时间要小于两步法。

参考文献：

[1] Cressie N A C.Statistics for Spatial Data[M].New York：Wiley，1991.

[2] Hallin M，Lu Z，Tran L T.Local Linear Spatial Regression[J].Annals of Statistics，2004,32(6).

[3] Gao J，Lu Z，Tjøstheim D.Estimation in Semiparametric Spatial Regression[J].Annals of Statistics，2006，34(3).

[4] Lin Z，Li D，Gao J.Local Linear M-estimation in Non-parametric Spatial Regression[J].Journal of Time，2009，30(3).

[5] Lu Z，Tang Q，Cheng L.Estimating Spatial Quantile Regression with Functional Coefficients:A Robust Semiparametric Framework[J].Bernoulli，2014，20(1).

[6] 王康宁，林路.空间非参回归的变量选择[J].中国科学：数学，2016，46(3).

[7] 周少甫，白羽.空间面板杜宾模型的Bootstrap Wald-COMPAC检验研究[J].统计与信息论坛，2016(5).

[8] 方丽婷.空间滞后面板平滑转换模型的估计及数值模拟[J].统计与信息论坛，2017(1).

[9] Zhang W，Lee S Y，Song X.Local Polynomial Fitting in Semivarying Coefficient Model[J].Journal of Multivariate Analysis，2002，82(1).

[10] Fan J，Huang T.Profile Likelihood Inferences on Semiparametric Varying-Coefficient Partially Linear Models[J].Bernoulli，2005，11(6).

[11] Wang H J，Zhu Z，Zhou J.Quantile Regression in Partially Linear Varing Coefficient Models[J].Annals of Statistics，2009，37(6).

[12] Kai B，Li R，Zou H.New Efficient Estimation and Variable Selection Methods for Semiparametric Varying-coefficient Partially Linear Models[J].Annals of Statistics，2011，39(1).

[13] 唐庆国.空间半参数变系数部分线性回归中的分位数估计[J].中国科学:数学，2013，43(9).

[14] Schumaker L L.Spline Functions：Basic Theory[M].New York：Wiley，1981.

[15] Huang J Z，Wu C O，Zhou L.Polynomial Spline Estimation and Inference for Varying Coefficient Models with Longitudinal Data[J].Statistica Sinica，2004，14(3).