基于单系统估计量的人口普查净覆盖误差估计

文 婷，吴 笛，胡桂华

（重庆工商大学，重庆 400067）

0 引言

人口普查的目标是不重不漏地登记普查目标内的每一个人。然而，由于各种主观或客观原因，使得普查结果总会有误差。在每次人口普查后，政府统计部门都要对普查数据的误差进行评估，其中的核心评估指标是净覆盖误差。

净覆盖误差定义为普查登记人口数与普查目标真实人口数之差。由于普查登记人口数已知，所以净覆盖误差估计的关键是寻求一个估计量去估计目标真实人口数。单系统估计量、双系统估计量和三系统估计量均可充当这个估计量［1-3］。

双系统估计量来源于捕获-再捕获模型，它把普查人口名单看作第一次捕获的结果，把事后计数调查人口名单看作第二次捕获的结果，捕获-再捕获模型给出了用两次捕获的个体数目以及同时出现在两次捕获中的个体数目估计总体中全部个体数目的计算公式［3］。它要求人口普查名单与事后计数调查人口名单相互独立。然而，这一要求在实际中常常不能满足，这时就会导致交互作用偏差，从而高估或低估目标真实人口数［4］。三系统估计量建立在三次捕获模型基础上，依据普查人口名单、事后计数调查人口名单、行政记录人口名单及这三份人口名单的人数及名单之间匹配的人数而构造［5-6］。相比双系统估计量，三系统估计量不要求这三份人口名单独立，而且三系统估计量利用了两个辅助信息，其估计精度会高于双系统估计量。然而由于三系统估计量在理论上和计算上都比较复杂，目前还不具备使用三系统估计量估计人口普查净覆盖误差的能力。

单系统估计量依据样本普查小区的事后计数调查人口名单而构造。相对于双系统估计量和三系统估计量，单系统估计量在计算上更为简便，其缺陷是没有使用辅助信息。本文研究单系统估计量在人口普查净覆盖误差估计中的应用。

1 单系统估计量及其抽样方差估计量

单系统估计量依据事后计数调查样本数据构造。本文采用以普查小区为抽样单位的分层二重抽样［7-9］方案。在第一重抽样中，按照地理位置，将所有普查小区划分在城市层和乡村层。使用H表示第一重抽样层的总层数，h表示任意一层，Nh表示h层的普查小区总数。在各个h层抽取第一重样本，样本量记作nh。在第二重抽样中，将第一重样本普查小区按照普查小区规模再次分层，共分为G层，g表示其中任意一层，Mhg表示层h中第一重样本普查小区进入层g的数目。每个g层仍然以普查小区为抽样单位抽取第二重样本，样本规模记作mhg。

最终进入第二重样本的第i样本普查小区的抽样权数αhgi为：

这里用yhgi表示在层hg中第i个样本普查小区某调查变量y的总人数，目标真实人口数Y的单系统估计量为：

在构造了单系统估计量之后，还要从抽样方差的角度来判断其估计精度。虽然单系统估计量是较为简单的估计量，但抽样理论指出，如果采用的抽样方法是复杂的，其估计量也会变得复杂。对于复杂估计量，其抽样方差通常采用分层刀切法、泰勒线性方差或者其他方法近似计算［10-13］。

这里使用分层刀切法计算单系统估计量的抽样方差。刀切法的关键在于复制权数和复制估计量的计算。复制权数是指在轮流刀切第一重样本普查小区后，重新计算进入第二重样本普查小区的抽样权数，记作和k表示刀切层s的样本普查小区k。

计算复制权数时可能出现的五种情况。①如果刀切的第一重样本普查小区k就是第二重样本普查小区i，此时样本普查小区i的抽样权数为0。②如果刀切的第一重样本普查小区k与第二重样本普查小区不在同一层，即s≠h，此时样本普查小区i的抽样权数不变，为αhgi。③如果刀切的第一重样本普查小区k与第二重样本普查小区i在同一个h层，但k没有进入第二重样本，也不在同一个g层，此时样本普查小区i的抽样权数变为[Nh/(nh-1)](Mhg/mhg)。④如果刀切的第一重样本普查小区k与第二重样本普查小区i在同一个h层，也在同一个g层，但k没有进入第二重样本，此时样本普查小区i的抽样权数变为[Nh/(nh-1)][(Mhg-1)/mhg]。⑤如果刀切的第一重样本普查小区k与第二重样本普查小区i在同一个h层，也在同一个g层，k进入了第二重样本，此时样本普查小区i的抽样权数变为[Nh/(nh-1)][(Mhg-1)/(mhg-1)]。

根据上述论述，被刀切的第一重样本普查小区k与剩下第二重样本普查小区i之间存在五种关系：

其中θhg为进入第二重样本普查小区的集合。此时被刀切后的单系统复制估计量为：

则单系统估计量的分层刀切抽样方差估计量为：

基于单系统估计量的人口普查净覆盖误差为Ŷ-C，C为普查登记人口数。

2 双系统估计量及其抽样方差估计量

为比较单系统估计量和双系统估计量在人口普查净覆盖误差上的估计精度，这里引入普查与事后计数调查独立情况下的双系统估计量［14-16］：

其中yhgi,v为层hg中第i个样本普查小区在等概率人口层v的人口数。

双系统估计量的抽样方差估计量为：

3 模拟分析

模拟的目标是使用单系统估计量及其方差估计量计算实际人口数及其抽样误差估计值，并与双系统估计量进行抽样估计精度比较。假设重庆市某城乡结合社区共有86个普查小区。按城乡分为城市层h1和乡村层h2，其中城市层有54个普查小区，乡村层有32个普查小区，分别记作N1=54，N2=32。从层h1中随机抽取8个普查小区，从层h2中随机抽取5个普查小区，记作n1=8，n2=5。所抽取的这13个普查小区称之为第一重样本普查小区。对抽取的第一重样本根据规模大小再次分层，分别记为g1,g2，其中规模大层有普查小区7个，规模小层有普查小区6个。从层g1中抽取6个普查小区，从层g2中抽取4个普查小区。所抽取的10个普查小区称之为第二重样本普查小区。样本形成及抽样权数见表1。

表1 样本形成、样本普查小区的抽样权数

对于进入第二重样本的普查小区，采取问卷调查的方式获得这10个样本普查小区的事后计数调查人口名单。将这份名单与人口普查名单进行比对，得到各层未加权的事后计数调查登记人口数和普查登记人口数，同时登记在这两份名单上的人口数如表2-表4。

表2 样本普查小区各层的未加权事后计数调查人口数（N2v） 单位：人

表4 样本小区各层的未加权匹配登记人口数（Mv）单位：人

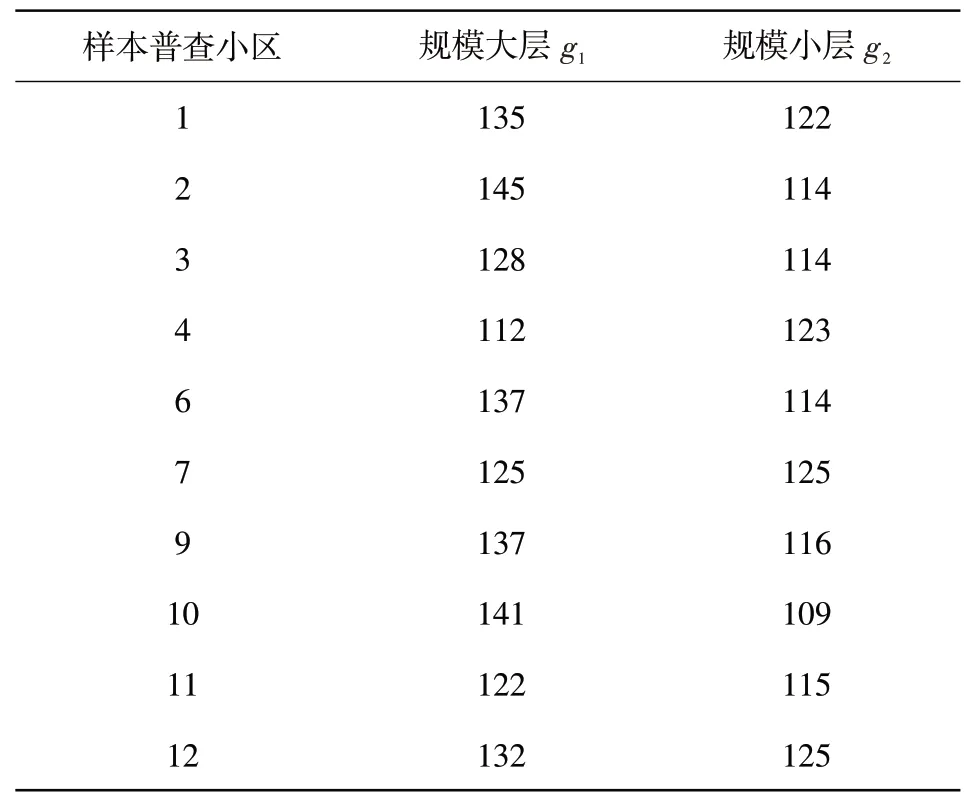
表3 样本普查小区各层的未加权普查登记人口数（N1v）单位：人

根据式（1）、式（2）、式（6）、式（7）和表2-表4，可分别计算出基于单系统估计量和双系统估计量的总体真实人口数。根据式（3）、式（4）、式（9）可计算出复制权数，单系统复制估计值和双系统复制估计值，根据式（5）、式（8）和上述计算结果可计算其抽样方差和人口普查净覆盖误差，其结果见表5。

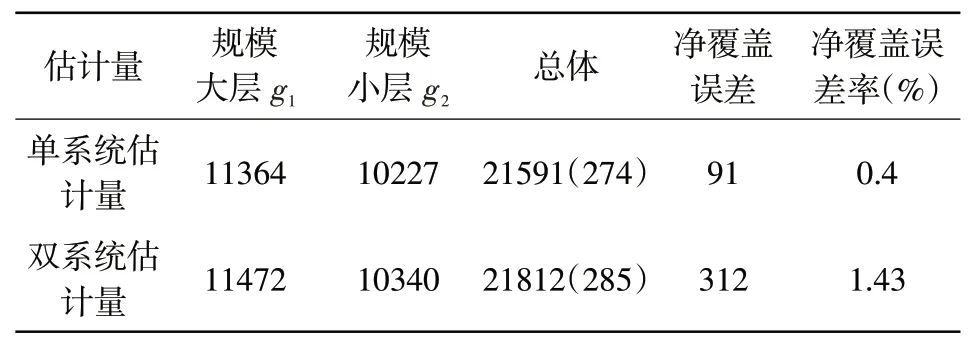
表5 各等概率人口层及总体真实人口数、抽样方差及其净覆盖误差 单位：人

从表5可以看出：（1）使用单系统估计量估计的总体实际人口数的抽样标准误差为274人，而使用双系统估计量总体实际人口数的的抽样标准误差为285人，这说明在抽样估计精度方面，单系统估计量优于双系统估计量；（2）如果每个普查小区平均住户250人，该社区共有86个普查小区，则该社区人数为21500人，若将这个人数当作普查登记人口数，单系统估计量估计的总体真实人口数为21591人，双系统估计量估计的总体真实人口数为21812人，则可计算出基于单系统估计量的人口普查净覆盖误差为91人，净误差率为0.4%，而基于双系统估计量的人口普查净覆盖误差为312人，净误差率为1.43%，这表明交互作用偏差使得双系统估计量高于实际人口数，人口普查净覆盖误差较高。高估的原因在于，在普查中登记过的人，认为已经参与了普查，没有必要再参加事后计数调查，这导致了这两项调查的匹配人口数少，而匹配人口数是双系统估计量的分母，从而使得双系统估计量高于总体实际人口数。

4 结论

第一，事后计数调查样本既可以采取分层抽样抽取，也可以采取二重抽样抽取。相较于分层抽样，分层二重抽样的样本代表性大，总体真实人口数的估计精度更高。

第二，如果不存在交互作用偏差，双系统估计量的抽样估计精度应该高于单系统估计量。如果存在交互作用偏差，双系统估计量中普查人口名单这一辅助信息的作用将会降低，单系统估计量可能优于双系统估计量。建议政府统计部门在决定使用单系统估计量还是双系统估计量之前，要采用恰当的方法判断普查与事后计数调查是否独立，只有在这两项调查独立的情况下，使用双系统估计量才是合适的选择。

第三，在分层二重抽样下，单系统估计量为复杂估计量，其抽样方差需要采用分层刀切等方法近似计算。采取分层刀切抽样方差估计量计算单系统估计量抽样方差的关键是复制估计值的计算。而计算复制估计值需要先计算刀切第一重样本普查小区后其余第二重样本普查小区的抽样权数，也就是复制权数。当前我国政府统计工作者尚未完全掌握分层刀切抽样方差估计量，建议统计部门聘请该方面的专家对工作人员进行培训，提高我国人口普查质量评估水平。