高中数学直观想象核心素养的培养

李木伟

（漳州市常山华侨经济开发区常山中学，福建 漳州 363307）

直观想象是指借助几何直观和空间想象感知事物形态与变化，利用图形理解和解决问题的过程。直观想象是发现数学结论和解决数学问题的重要素养，表现在能利用图形探索和解决数学问题，构建数学问题的直观模型。［1］数学题型种类繁多，由于学生认识面窄，知识储备量薄，知识运用能力弱，特别是在定义、平面几何及综合题等方面更显突出。笔者学校近几年质量监控情况，结合平常教学，认为直观想象核心素养应始终贯穿于以下几方面的教学。

一、定义教学与直观想象的培养

在中学数学教材中，常常采用“定义”的方式来引入某个数学概念，然后通过系列的推理得出此概念的本质属性，再直观运用此概念去解决数学问题。理解定义是解题的前提，也是核心，它有助于提升学生的直观想象能力。

例如，请根据平方根的定义，完成下列问题：

（1）求下列式子的x取值范围；

①

（2）求下列方程的解。

①

分析：本题主要考查平方根定义知识的运用，平方根定义是“如果一个数x的平方等于a，那么x叫做a的平方根，即在这个定义的教学过程中，教师因强调平方根的结果及被开方数的双非负性，而忽视了学生直观想象的培养。

（1）教师可根据定义的内涵，抓住被开方数是非负数，分析被开方数可以由数和字母组成，进而让学生体会到由特殊到一般的变化，以训练学生严密的思维。教师通过引导，学生很自然地得出此类型题目的解题方法

（2）对于第一小题通过与定义直观的对比，学生很容易得出 的值；第二小题通过分析想象，使平方根的定义与一元二次方程解法有机融合，进行作直观的对比，让两个知识点之间得到横向联系，求出方程的解。

二、平面几何题教学与直观想象的培养

平面几何研究的对象是形象直观的图形，而图形是平面几何中思维借以展开的依据。在平面几何，例如在线段、角、三角形等教学中多做直观演示，在演示中，要特别引导学生注意观察，给学生提示应注意什么，问学生发现了什么，通过观察和引导使学生获得几何直观和空间想象思维的感性认识。

（一）图形规律教学与直观想象的培养

在图形规律教学中，要着重培养学生发现直观图形规律，并利用图形的规律解决问题的能力。如1，学生数线段时易数错，此时应引导学生通过直观观察，考虑每条线段都有两个端点，抓住一个端点不变，另一个端点变化的思路，就可以找到所有线段。

图1

图2

图3

经过以上训练，对于图2和图3，学生就不难数出角和三角形的数量。以上问题虽然简单，但对于初学平面几何的学生来讲，的确有助于学生对图形想象及图形的分析能力提升。

（二）基本图形教学与直观想象的培养

徐立瞿在《基本图形分析法》一书中指出，组成一个几何问题图形的最简单、最重要、最基本的，但又是具有特定的性质，能明确地阐明应用条件和应用方法的图形，称为基本图形。［2］在平面几何教学中，教师常常遇到一些较为复杂的图形，但也能把它分解成几个相类似的基本图形，从而培养学生观察、分析和思考能力。

例如，“在直角三角形中，两锐角互余”教学中，这是直角三角形这个基本图形的一个基本性质，学生很容易掌握，但对由这个基本图形组成的图形，学生会通过直观想象找出思路和解决的办法。观察图4，说出图中有几个直角？哪些角互余？哪些角相等？此题的基本图形是直角三角形，根据上述性质，本题的所有问题将迎刃而解。同时，在教学过程中，可以引导学生想象，当∠BAD和∠C满足什么条件时，△ABC为直角三角形或等腰三角形。

在教学中，教师常遇到一些图形，它们须通过作辅助线，才能找到它们构造的基本图形，因此教师不仅要安排这方面的训练，而且要引导学生会用有关知识去观察、想象、分析，从而达到培养学生直观想象能力的目的。

图4

（三）图形变换教学与直观想象的培养

在平时教学中，教师常遇到图形的基本变换（图形所作的平移、轴对称图形的翻转，中心对称图形的旋转等），这些都是考查学生对轴对称图形与中心对称图形的理解，以及轴对称图形、中心对称图形与全等形之间的联系。应有意识地渗透几何变换的观点，使学生观察到由静到动的变化，从而实现思维能力从几何直观到空间想象的飞跃。

如图5，已知∠ADB=∠EDC，AD=BD，ED=DC，求证：AC=BE.

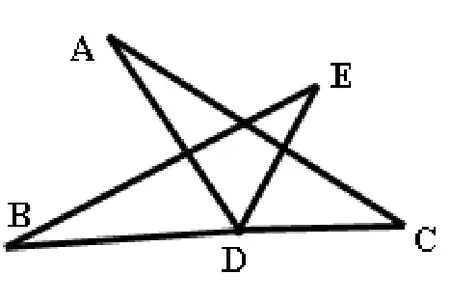
图5

图6

本题只要证明△ADC≌△BDE即可。证明时，我们还可以得出△ADC是由△BDE绕点D旋转一个角度得到。通过想象，可以把上述例题包装为：如图6，在线段BC同侧分别以BD、DC为边作等边三角形△ABD和△DCE，连接BE、AC，分别交AD、ED于M、N.求（1）DM=DN；（2）△ADC、△MDE怎样才能分别到达△BDE和△NDC的位置呢？图形变换的题目往往可以产生“一题多问”“一题多思”，教学中要让学生勤于观察、善于思考，才能发现、理解题目的内涵，促进直观想象能力的提升。

三、综合题教学与直观想象的培养

在农村学校，教师发现很多学生对综合性题目的处理能力都较弱，特别是涉及“动态”的问题，学生都很茫然，无从下手。在教学中，教师加强直观想象的培养，让学生从分析题意的过程中，感受综合题是由几个基础知识相互交叉组成的，并不是不可以逾越的高峰。

如图7，一次函数y=-2+3的图象交轴于点A，交y轴于点B，点P在线段AB上（不与点A、B重合），过点P分别作OA和OB的垂线，垂足为C、D，求（1）△AOB的面积；（2）点P在何处时，矩形OCPD的面积为1.

本题涉及三角形、函数及一元二次方程等知识，信息量大，直观知识多，想象空间广。教师在本题的教学中，先让学生夯实相关知识点，再引导学生可以从几个方面对题目进行改造。

（1）一次函数y=-2x+3的解析式不直接给，通过改造条件，告之点A的坐标或者A和B的坐标等方式，考查一次函数解析式的求法。

（2）“点P在线段AB上（不与点A、B重合）”这个条件转化为动点问题“点P从点A出发，沿AB方向运动”，感受动态问题的解题思路——化动为静，“动”是迷惑的表面现象，“静”是满足条件的目标。

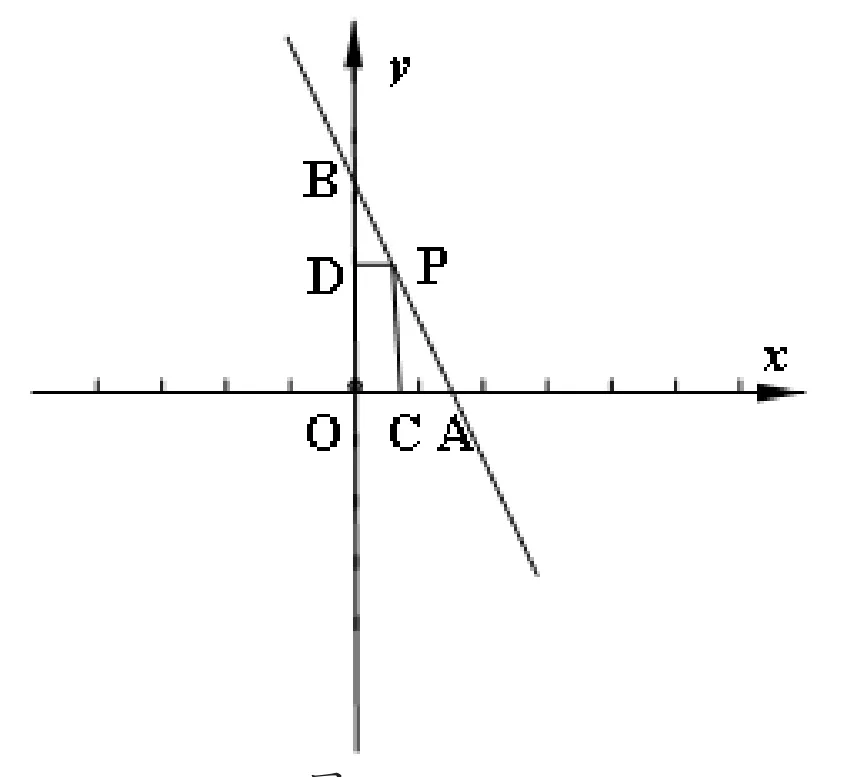
图7

（3）以求矩形OCPD的面积进行拓展，①矩形OCPD的面积与△AOB的面积之间的倍分关系，可以加强数学思想方法教学；②当矩形OCPD的面积取得最大值时，求过点P、A、O的二次函数的解析式。

在进行综合题的训练时，首先得要求学生掌握定义、公式、法则等知识，同时应注意展示各知识之间横纵联系，及时将所学的知识进行整理和归类，使学生想象问题的能力更有条理性、针对性，减少“想”的盲目性。在学习中要运用过去所获得的知识包括接受学习中获得的知识，通过运用这些知识可以使这些知识得到巩固或者获得新的理解。［3］

总之，教师要着力于学生的基础知识教学，还要着力于培养学生独立思考问题的习惯，发展学生的思维能力，关注学生数学核心素养的培养，同时让学生明白“授之以鱼，不如授之以渔”的道理。

［1］黄炳锋.充分发挥技术作用发展学生的数学核心素养［J］.福建基础教育研究，2016（10）.

［2］徐立瞿.基本图形分析法［M］.郑州：大象出版社，1998：12.

［3］ 施良方，崔允漷.教学理论［M］.上海：华东师范大学出版社，1999：131.