砂土中筒型基础静压下沉试验及受力特性
2018-06-12朱小军李文帅龚维明
朱小军 李文帅 龚维明 费 康
(1东南大学土木工程学院, 南京 210096)(2扬州大学建筑科学与工程学院, 扬州 225127)
筒型基础是一种常见的海洋工程基础形式,沉贯安装是筒型基础施工过程中的关键步骤,多数筒型基础采用负压下沉安装,但负压沉贯过程中地基土体易发生渗透破坏、超高土塞、不能沉放到位甚至筒壁屈曲等工程事故.因此筒型基础的安全沉放离不开对沉贯负压的控制,合理的负压能在保证地基稳定的前提下大幅度减少筒体下沉阻力,并实现沉放到位.而筒体下沉预估所需负压的计算方法一般采用静力触探实测数据,而静力触探测定为静压下沉过程中土体阻力特性,与负压下沉筒土作用过程有较大差异.为提高采用静力触探方法估算负压下沉阻力的准确性,有必要对筒型基础静压下沉进行研究.
Andersen等[1]总结了一系列在密砂中裙板式基础的静压沉放原型测试及模型试验,提出侧壁阻力按照桶-土摩擦,桶端阻力基于地基极限承载力理论进行计算.陈飞[2]在饱和砂土中针对传统筒型基础结构和宽浅式筒型基础结构,分别开展了筒型基础静压沉放试验,发现筒壁下沉过程中存在明显的挤土效应;传统筒型基础还存在土塞效应.刘润等[3]通过模型试验研究了无黏性土中筒型基础静压下沉阻力,认为筒体下沉所需贯入力的增长速度随深度而增加;并结合基础承载力公式提出了考虑筒内外挤土差异的桶端阻力计算方法.霍知亮[4]采用速率控制法和力控制法对筒型基础进行静压下沉试验发现,土塞隆起接触到桶盖时,桶-土形成整体使得下沉阻力明显增大.闫澍旺等[5]采用耦合的欧拉-拉格朗日分析方法通过位移控制法和力控制法2种下沉方式,得出不同强度的黏土中筒型基础下沉阻力和下沉深度的关系及土塞高度.杨旭等[6]针对土体大变形和接触非线性等问题,建立筒型基础动态、连续沉放过程的有限元模型,模拟出静压下沉过程中筒壁内外侧挤土效应的差异情况.李大勇等[7]分析了砂土中筒壁摩阻力和筒尖端承载力随埋深的变化关系,认为筒基础内部土体提供了较大部分的承载力,而外壁摩擦力及尖端承载力贡献较小.
Randolph等[8]将拱效应的理论首次引入土塞效应中.贾海莉等[9]提出土拱理论中拱脚的存在形式、拱形、拱体几何参数及微观特性等几个值得探讨的问题,认为拱脚的存在形式有直接拱脚、摩擦拱脚、土体拱脚及二异拱脚4 种.
综上所述,对于筒型基础的沉贯过程阻力变化的研究从理论试验的角度出发,均发现筒-土摩阻力、土塞、沉贯阻力三者之间相互影响.本文开展了筒型基础模型在砂土中静压沉贯试验,旨在揭示静压下沉中由于土拱效应引起的筒体内土压力增加、端阻力发挥程度,以及筒内土塞的发展变化过程.
1 筒内土拱计算分析
土拱的形成是在荷载作用下土体产生不均匀位移调动自身抗剪强度以抵抗外荷载的结果,故其拱形及结构是合理的,这种拱形被称为合理拱轴线[9].合理拱轴线的受力特点是拱体单元剪力和弯矩均为零,只受轴力作用.土拱在外力作用下能产生一定的位移而不破坏符合静定三铰拱的受力模式,在均布荷载作用下拱轴线方程为抛物线.
为分析筒壁对土体的约束而对内壁土压力产生的影响,做以下假定:① 筒壁粗糙且不发生变形;② 填土均匀无黏性;③ 筒壁与接触土体充分摩擦.
筒型基础土拱为三维,即厚壳结构为轴对称状态的空间土拱,在空间内有一对称轴,壳体中面是由一条和对称轴共面的曲线绕对称轴旋转构成.根据计算力学理论,将其简化为一个包含对称轴和经线的平面问题进行研究,取平面土拱进行分析;因上覆土重力和筒壁的摩擦影响,小主应力发生向上偏斜,使两侧筒壁之间的主应力轨迹线形成连续拱曲线,即为小主应力拱,其应力状态可用莫尔应力圆表述(见图1).图中,σ3为拱内小主应力;φ为土体内摩擦角;σh,σv为水平、竖向应力;θ为特征角.
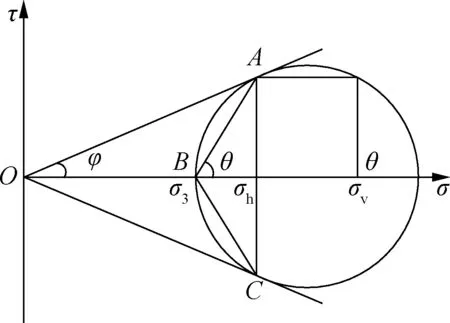
图1 拱线受力图
假设合理土拱的厚度为t,拱高为f,根据三铰拱的静力平衡条件对土拱进行受力分析,如图2所示.图中,q为土拱上部均布荷载;qu为土拱底部承载力;V1为拱支座处的竖直反力;H1为拱支座处的水平反力;d为拱直径;σ1为拱内大主应力.竖直反力和水平反力计算式为
(1)
(2)
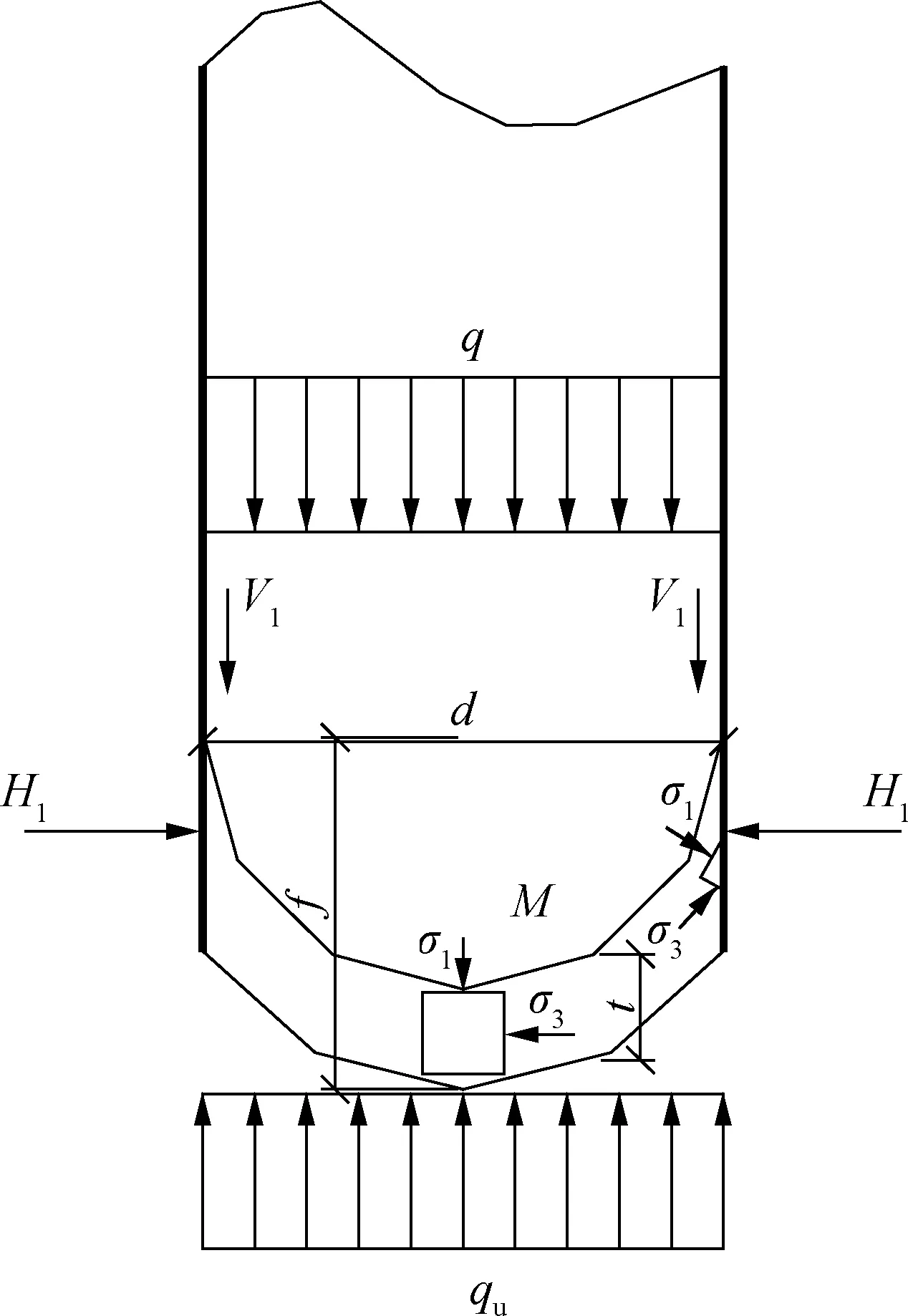
图2 土拱效应示意图
土拱的跨中界面处是最不利的位置,其应力状态为
(3)
σ1=q
(4)
筒内土拱的极限控制条件与M点相同,根据土体极限平衡状态可知
(5)
联立式(3)~(5)得到
(6)
拱脚处的极限平衡状态为
V1=H1tanφ
(7)
联立式(1)、(2)、(6)、(7)得到
(8)
联立式(1)、(8)得到
(9)
根据静力平衡条件可知,土拱效应引起的土体剪力T与V1相等,根据摩擦学原理[10]剪应力τ与法向应力之间存在如下关系:
(10)
式中,μ为土与筒裙的摩擦系数;σharc为土拱引起的水平土压力.
筒体内部总土压力为
σ=σ0+σharc
(11)
式中,σ为内部总土压力;σ0为静止土压力,σ0=qK0,K0为静止土压力系数.
2 筒型基础静压下沉模型试验
2.1 试验装置
筒型基础室内模型试验装置主要由加载系统、筒型基础模型、模型槽及测读系统组成.其中,模型槽尺寸为1 500 mm×1 000 mm×1 200 mm(长×宽×高),正面一侧为钢化玻璃,其余4面为钢板.测读系统由应变采集仪、量力环、LDT传感器、土压力盒及数码相机组成,装置示意图如图3所示.
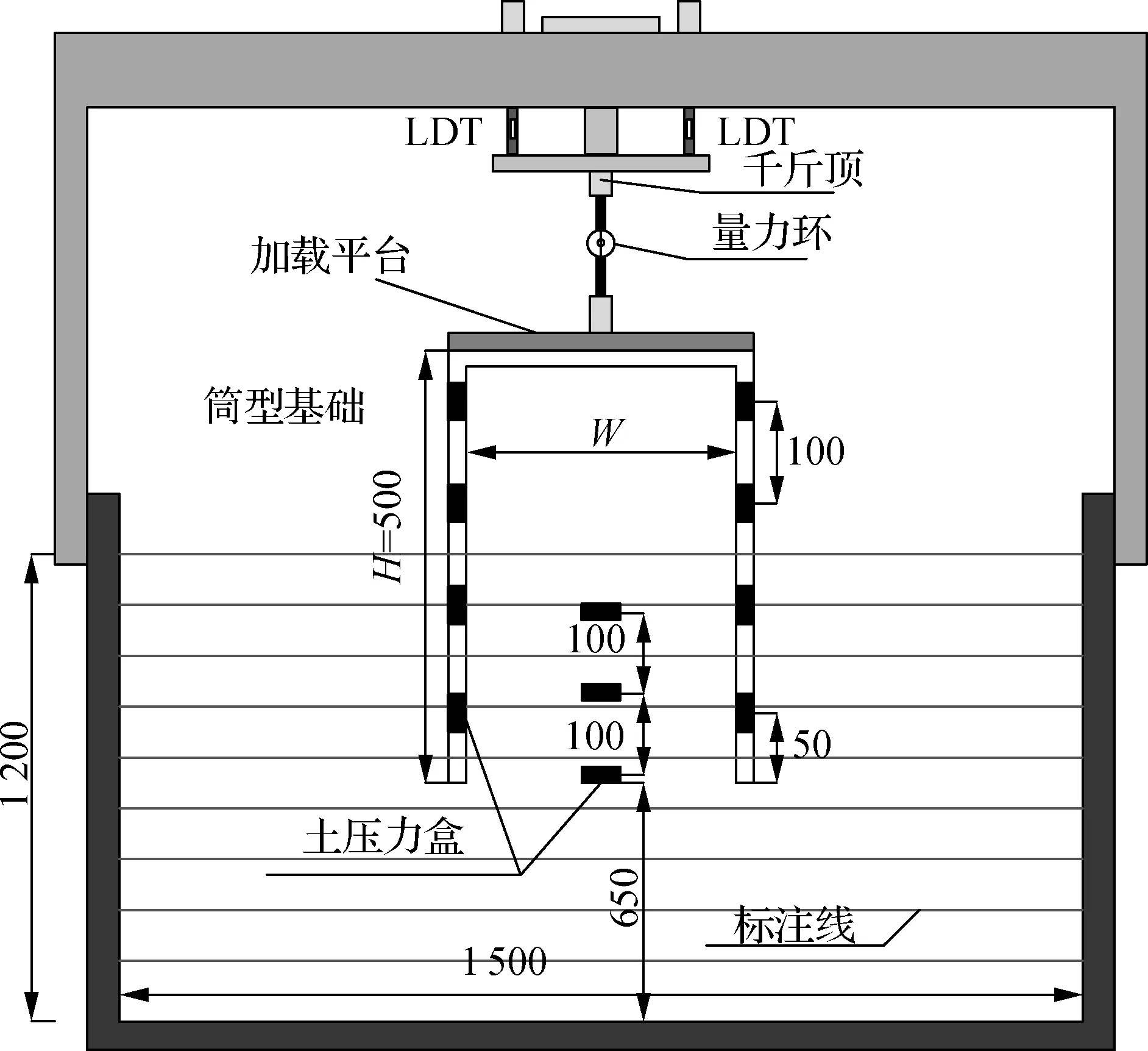
(a) 模型示意图

(b) 模型实物图 (c) 土压力盒布置图3 试验装置示意图(单位:mm)
2.2 筒型基础模型
筒型基础模型采用半模钢筒,模型尺寸如表 1所示.为研究筒体下沉过程中筒土相互作用,在筒体内外壁预留凹槽位置处分别布设4个土压力盒,间距为100 mm,受力面朝向土体.内侧土压力盒由上向下依次记为I-1,I-2,I-3,I-4,外侧记为O-1,O-2,O-3,O-4,如图3(c)所示.其中,最下端土压力盒(O-4,I-4)距离筒体端部50 mm;在筒型基础的顶部预留孔洞以便内部土压力盒的导线引出.沿筒型基础贯入的轴向方向依次预埋3个土压力盒,间距为100 mm,由上向下依次记为P-1,P-2,P-3.
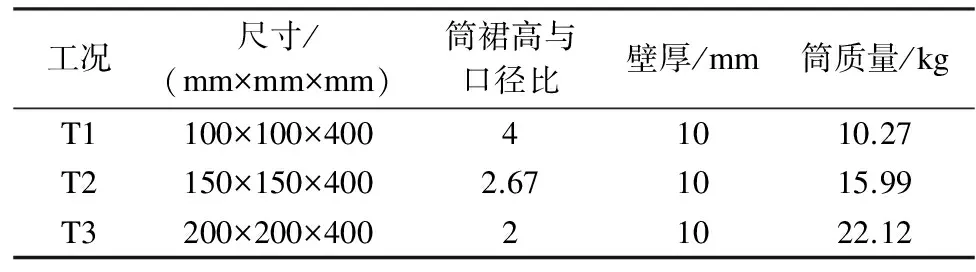
表1 各工况模型尺寸
2.3 试验土体
试验地基土采用石英砂,颗粒级配曲线见图4.填砂时控制一定的落砂高度,分层摊铺,每层厚度为5 cm,根据砂土密度及每层体积计算出每层砂土质量,分成压实,整平至设计高度,并铺设染色砂作为分层标记.每填一层后静置12 h,以保证每次试验样本的均一性.试验用砂内摩擦角为32.6°,重度为15.6 kN/m3,相对密度为0.67,不均匀系数为3.24,曲率系数为0.573.
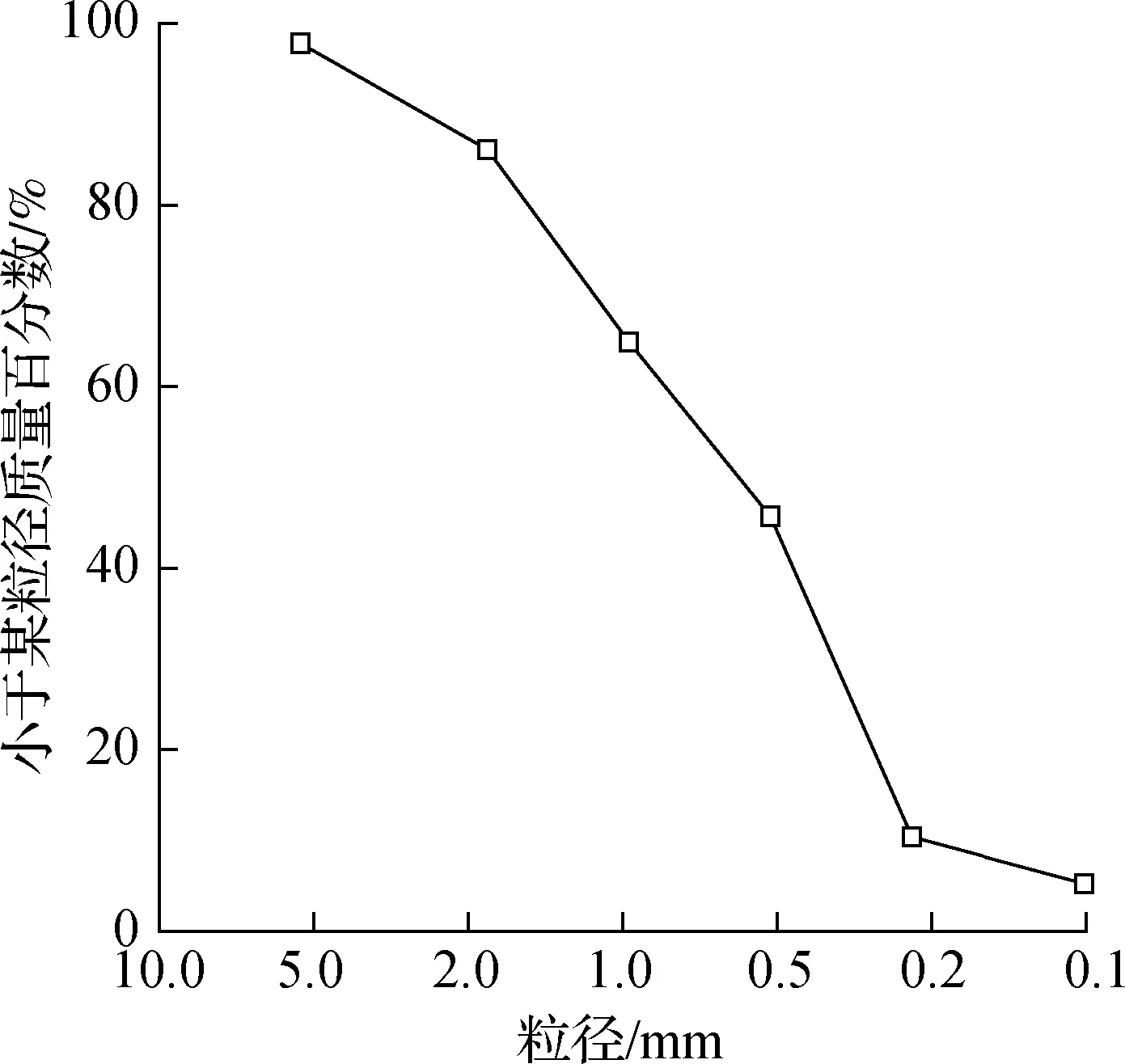
图4 粒径级配累积曲线
2.4 试验方法与过程
试验前在钢化玻璃内侧涂抹凡士林以减小筒型基础与钢化玻璃的摩擦,试验时采用静压沉贯,位移控制沉贯深度,每级加载位移3 mm.每级位移加载完成15 min后,分别采集土体位移场和土压力盒数据,同时记录筒体内部土塞的发展状况,因土压力测量的离散性,每个工况均进行平行试验,以保证试验的合理性.
3 静压下沉试验结果分析
3.1 土压力分析
3.1.1 内壁土压力分析
图5为I-4土压力盒实测结果及其根据式(11)的计算结果.因工况T2,T3的实测值曲线较为接近,取其中一条与工况T1进行对比分析.可以看出,筒壁内侧土压力随入土深度的增加而迅速增大,这与Randolph等[8]研究的管桩内侧土压力随深度指数级增长的理论解类似.结合1.1节计算可知,在筒体下沉过程中,内部土体产生不均匀变形形成土拱效应,导致内部土压力增大. 各工况与实测结果较为吻合,可验证本文考虑土拱效应时推导出土压力理论公式的合理性.
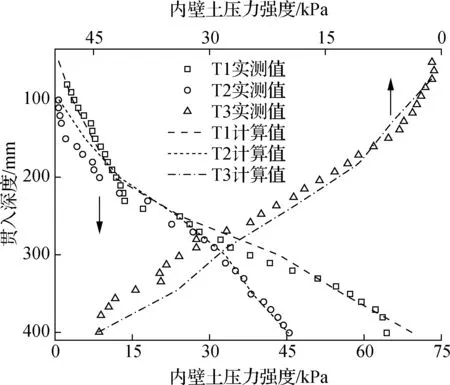
图5 内壁土压力曲线图
3.1.2 外壁土压力分析
筒体踏面对下部土体产生约束作用形成楔形弹性压实核,此时筒体踏面与基础底面类似,压实核随筒体同步下沉.根据Terzaghi[11]假设,刃脚踏面与压实核的夹角为45°+φ/2.由于端部踏面土受到挤压排向筒壁内外侧,当筒壁进入土体的体积大于土体的压缩量时,筒壁外围的土体涌向筒壁产生非静止土压力,因此,外壁土压力可以采用考虑变形的朗肯土压力[12]计算式,即
(12)
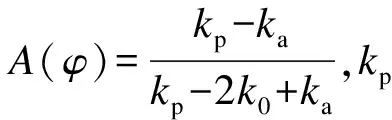
文献[13]认为,达到主动土压力时的位移量为(-0.001~-0.003)h,h为挡土结构物的高度,即为sa,而达到被动土压力时的位移量为(0.02~0.05)h.设筒型基础达到被动土压力极限值所需的位移量sP= 5%h= -15sa,取向填土方向移动为正;根据不同的土塞闭塞程度对筒外土体位移s进行取值,如表2所示.
由图6土压力盒O-4可见,各工况实测值与式

表2 外部土体位移取值
(12)计算值的发展趋势相同,二者之间基本吻合.工况T2,T3的实测值接近,与折减系数为0.247的计算值吻合度较好.
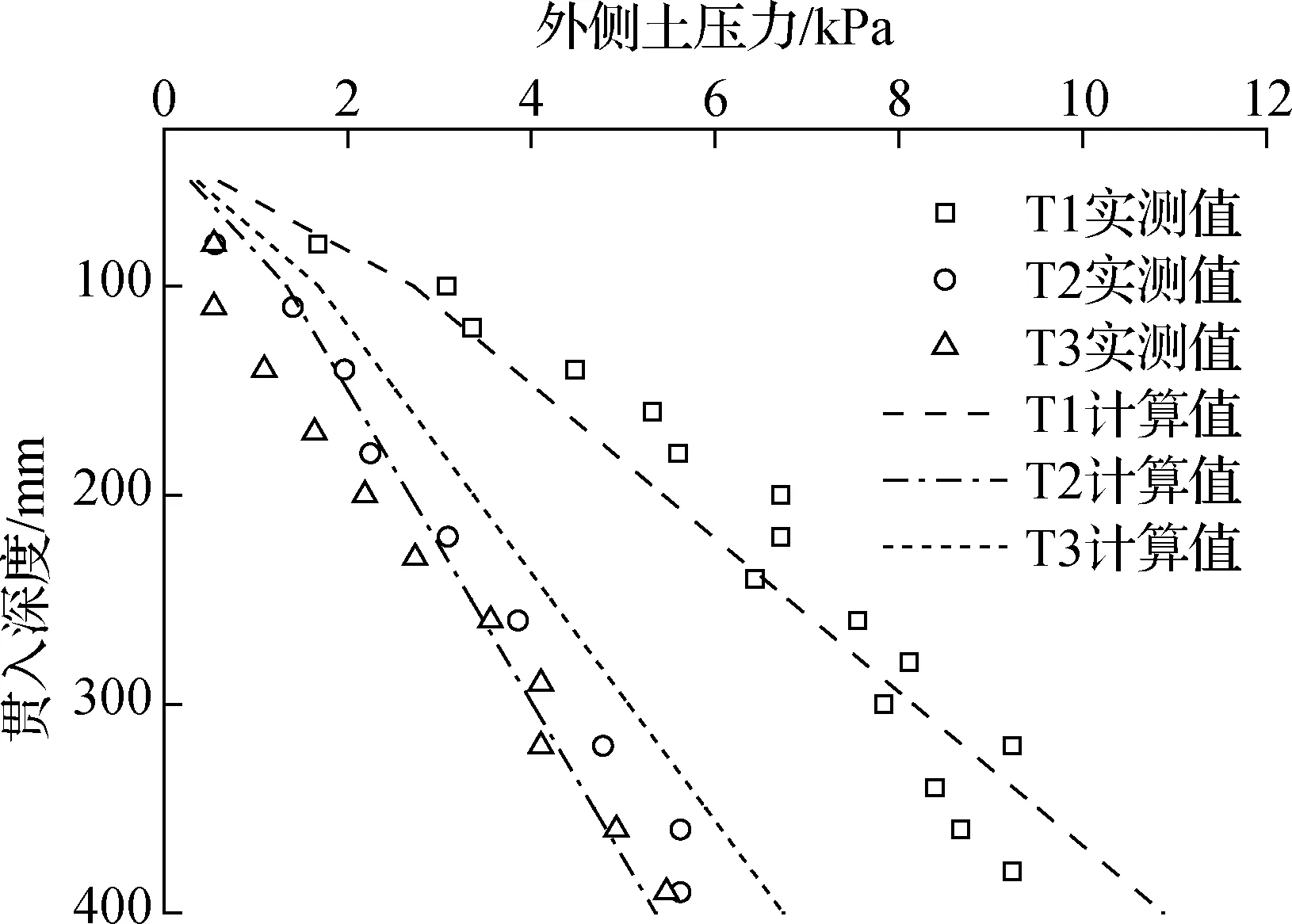
图6 外壁土压力曲线图
3.1.3 筒体内部土压力
筒体沉贯过程中各工况土塞内部的土压力盒实测值如图7所示,工况T1的土压力值最大,T2,T3的土压力值较为接近;但各工况土压力峰值均出现在筒体端部,即刚好贯入到预埋位置(见图7中),其后压力盒进入筒体内部,土压力值随贯入深度逐渐减小.可见在筒体贯入土体过程中,其端部以下土层形成土拱,其后土拱被挤压滑移至筒体内部,所以各工况的土压力盒P-2进入筒体内后,在土拱的保护下量测值基本保持不变.结合图7可知,T1的闭塞程度较T2 ,T3大,因此,拱效应与土塞的闭塞程度之间成正相关关系.
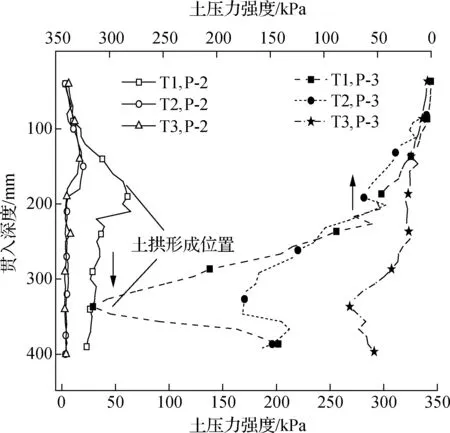
图7 内部土压力盒实测值
3.2 沉贯阻力与预测
在沉贯过程中当下沉力与自重满足下式时筒体即可下沉:
F+G=R=Rfo+Rfi+Rtip+Rfarc
(13)
式中,F为贯入力;G为模型自重;R为总阻力;Rfi,Rfo为内、外摩阻力;Rtip=quAtip为端阻力,Atip为筒底踏面面积;Rfarc=V1为土拱阻力.
各工况中静压沉贯筒体所需的贯入力如图8所示,在沉贯过程中贯入力随深度增加,前期贯入阻力呈线性增加,当贯入深度达到200 mm时贯入阻力陡增,各工况的贯入力发展趋势类似.在200 mm深度时开始出现土塞现象,工况T1在贯入深度达到300 mm时,贯入力较工况T2,T3更大,表明其筒内土塞效应更为明显.
由图8、图9可知,在贯入过程中随口径的增大贯入力逐渐减小,但土拱效应引起的阻力占总阻力的百分数逐渐增大,最高可达总阻力的70%.
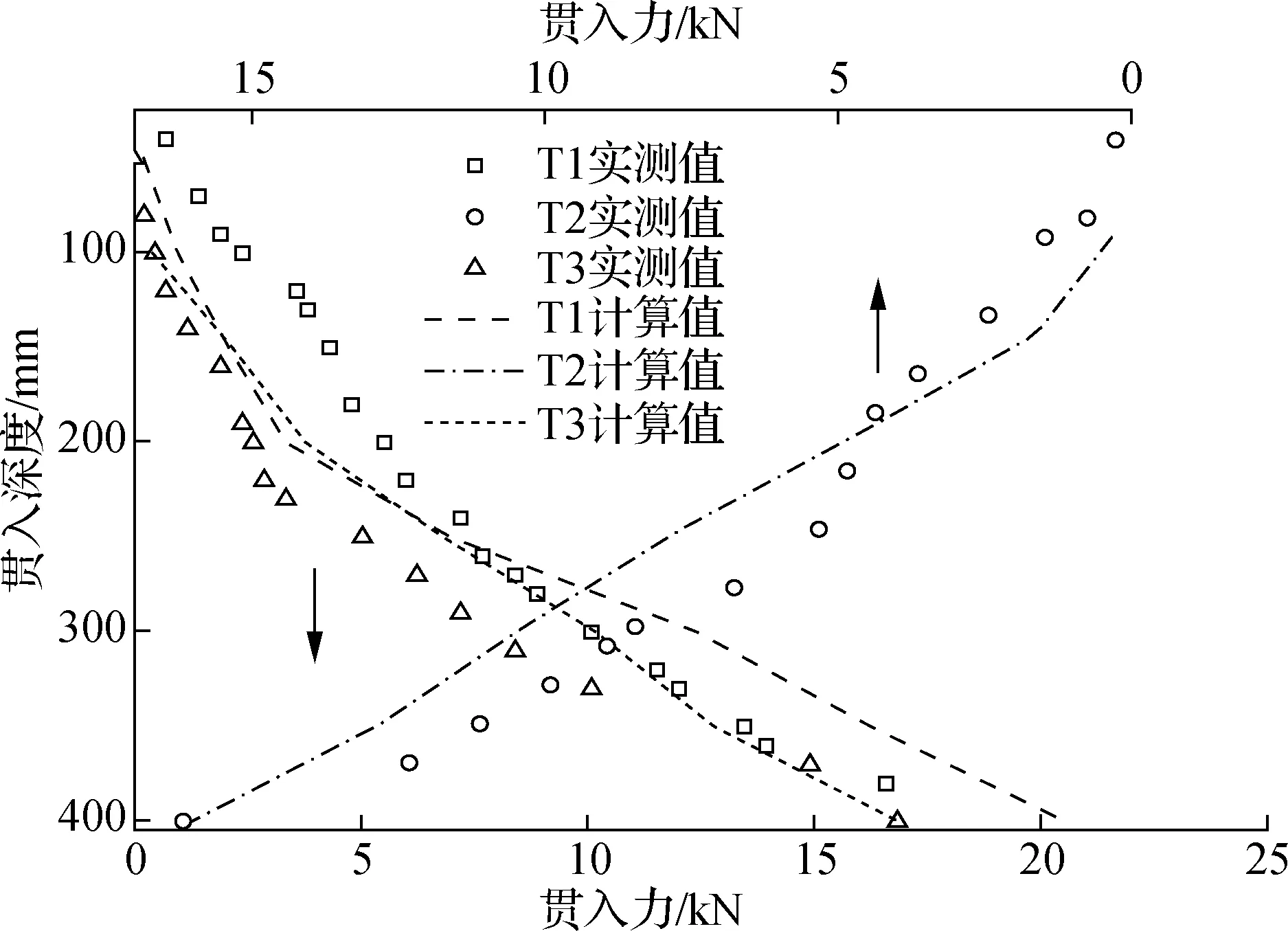
图8 贯入力曲线图
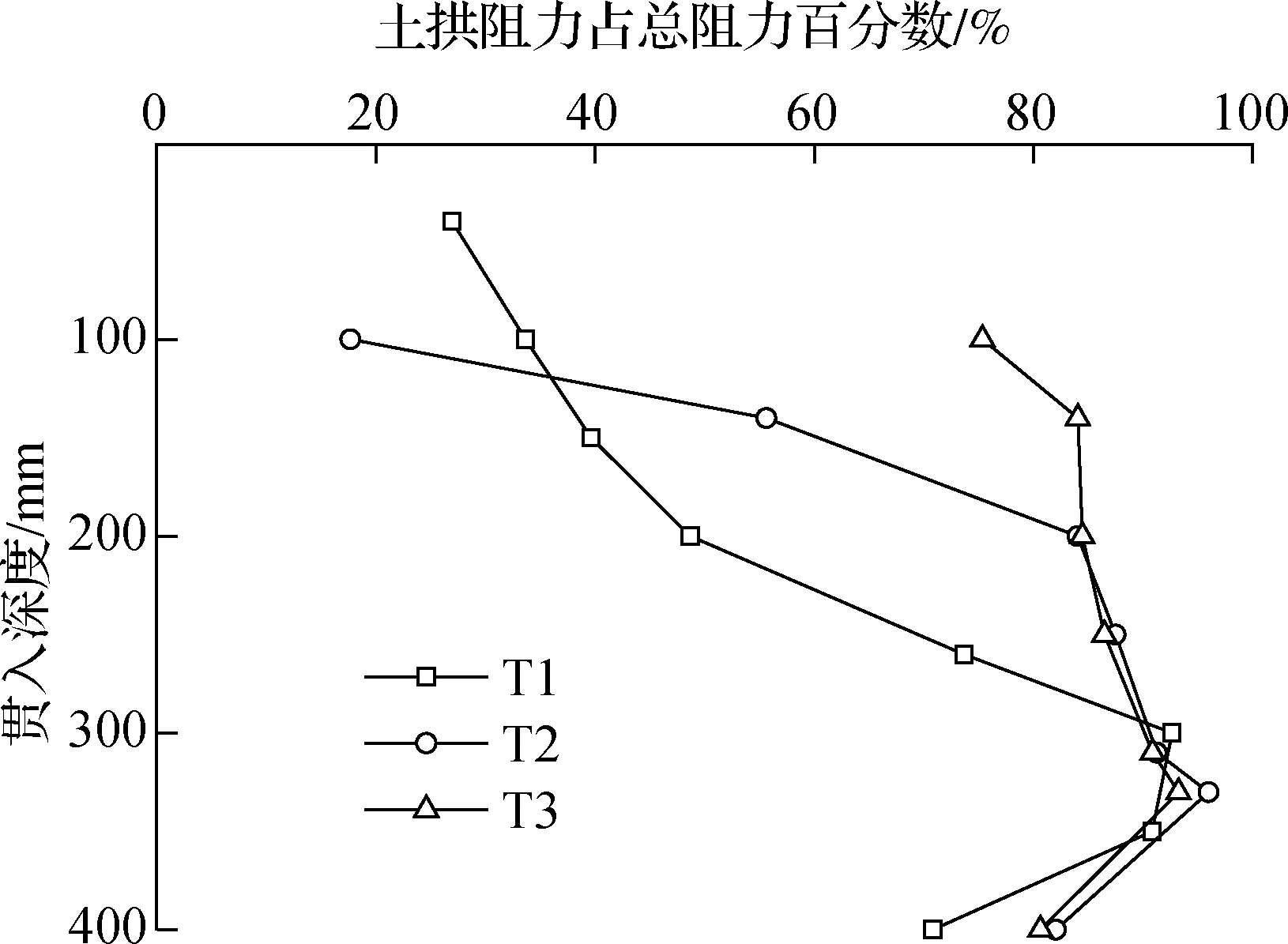
图9 土拱阻力占贯入阻力的百分数
3.3 端阻力分析
图10中工况T1的端阻力较T2,T3大,在前期三者均呈线性增大,在贯入深度为200 mm时均成指数级增长,沉贯结束后工况T1的端阻力远大于T2,T3,其原因是T1闭塞程度较二者大,但3个工况的端阻力均远小于总的沉贯阻力R,这与李大勇等[7]的试验结论吻合.
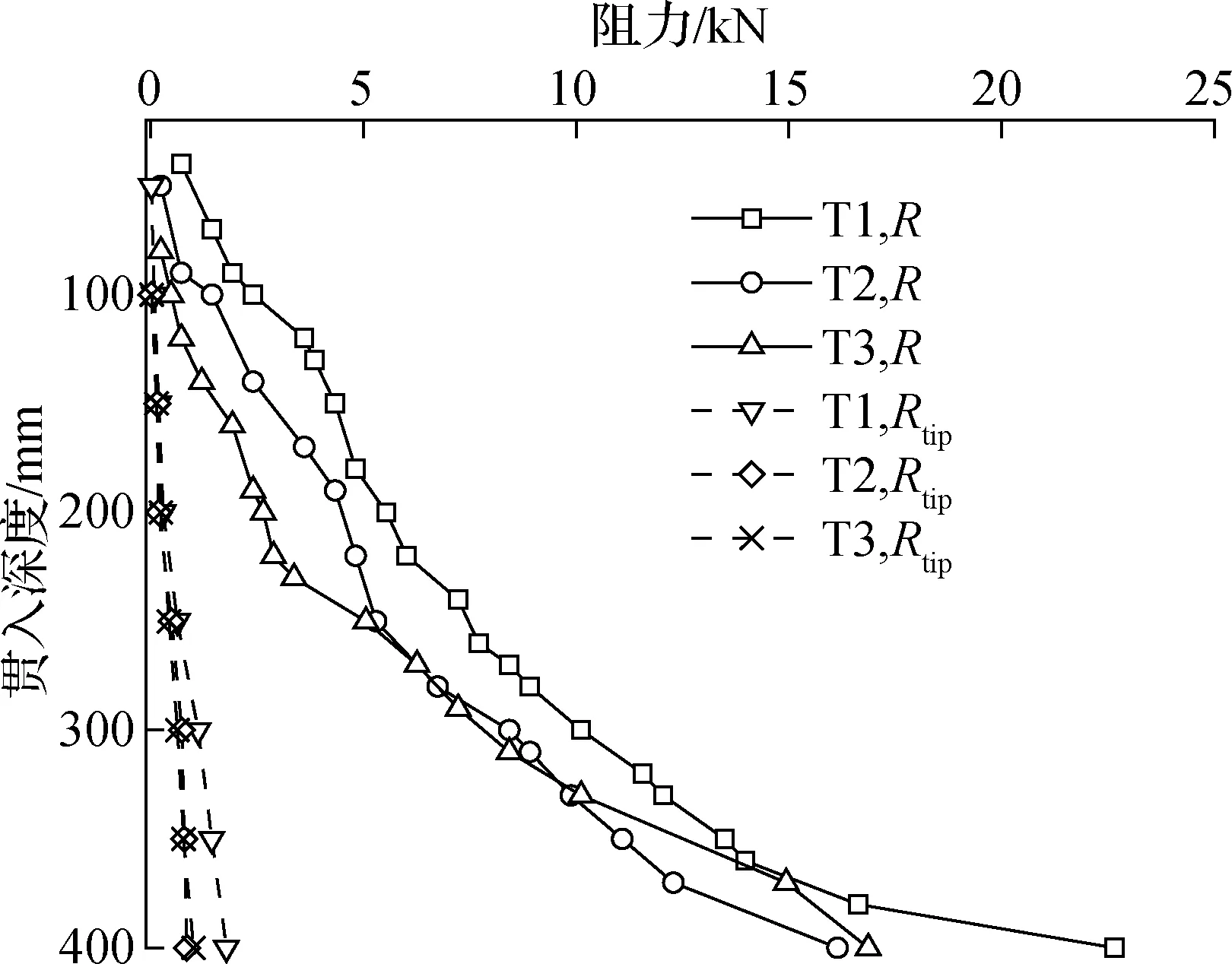
图10 筒端阻力变化曲线
3.4 沉贯过程中土塞的发展趋势
通常描述形成土塞的指标有土塞率RL和土塞增长率RI.RL定义为土塞长度L与贯入深度D的比值,即
(14)
式中,L为土塞长度;D为筒体的入土深度.
RI定义为土塞长度增量与贯入深度增量的比值,即
(15)
式中,dD为筒体的单位贯入增量;dL为筒体单位贯入增量为dD时的土塞高度增量.用土塞增长率描述开口筒型基础的闭塞程度,土塞增长率值越小表明筒体内部土体闭塞越明显,当RI= 0 时筒体处于完全闭塞状况;当RI= 100%时,为完全不闭塞的内核状况.
在沉贯过程中土体在筒壁的作用下产生剪切滑动,宏观表现为筒壁端部刺入土体.随着筒体入土深度的增大,土塞长度随之增大,土-筒壁之间的摩阻力增大,带动筒内土塞产生向下的位移,筒内土塞高度开始逐渐低于原土面高度,筒内土颗粒经历一个逐渐压缩密实楔紧的过程;靠近筒壁的砂土颗粒剪切位移较大,宏观表现为靠近筒壁的染色砂颗粒向下移动,产生一个上凸的‘拱形’,如图11所示.
由图12(a)中可以看出,工况T1,T2在筒体下沉深度小于190~290 mm时,土塞增加的高度与筒体入土的深度相同,在深度大于290 mm时土塞的长度逐渐小于筒体的下沉深度;工况T1中口径较小,初始贯入阶段出现明显的挤土现象导致土塞率值大于1,在贯入深度大于150 mm后土塞长度开始小于筒体贯入深度.

图11 T2土塞形成示意图
图12(b)为各工况筒体贯入过程中土塞增长率的变化情况,工况T1在初始阶段土塞增长率大于100%,并随着贯入深度的增大而减小,沉贯结束时土塞增长率为65%,筒体闭塞较为显著;在工况T2和T3贯入深度至200 mm时RI<100%,土塞效应与图8贯入力在200 mm深度处开始陡向增长吻合;在沉贯结束时土塞增长率分别为70%和80%,此时土塞处于不完全闭塞状态.黄生根等[14]型基础在贯入深度达到1倍口径时土塞开始形成.
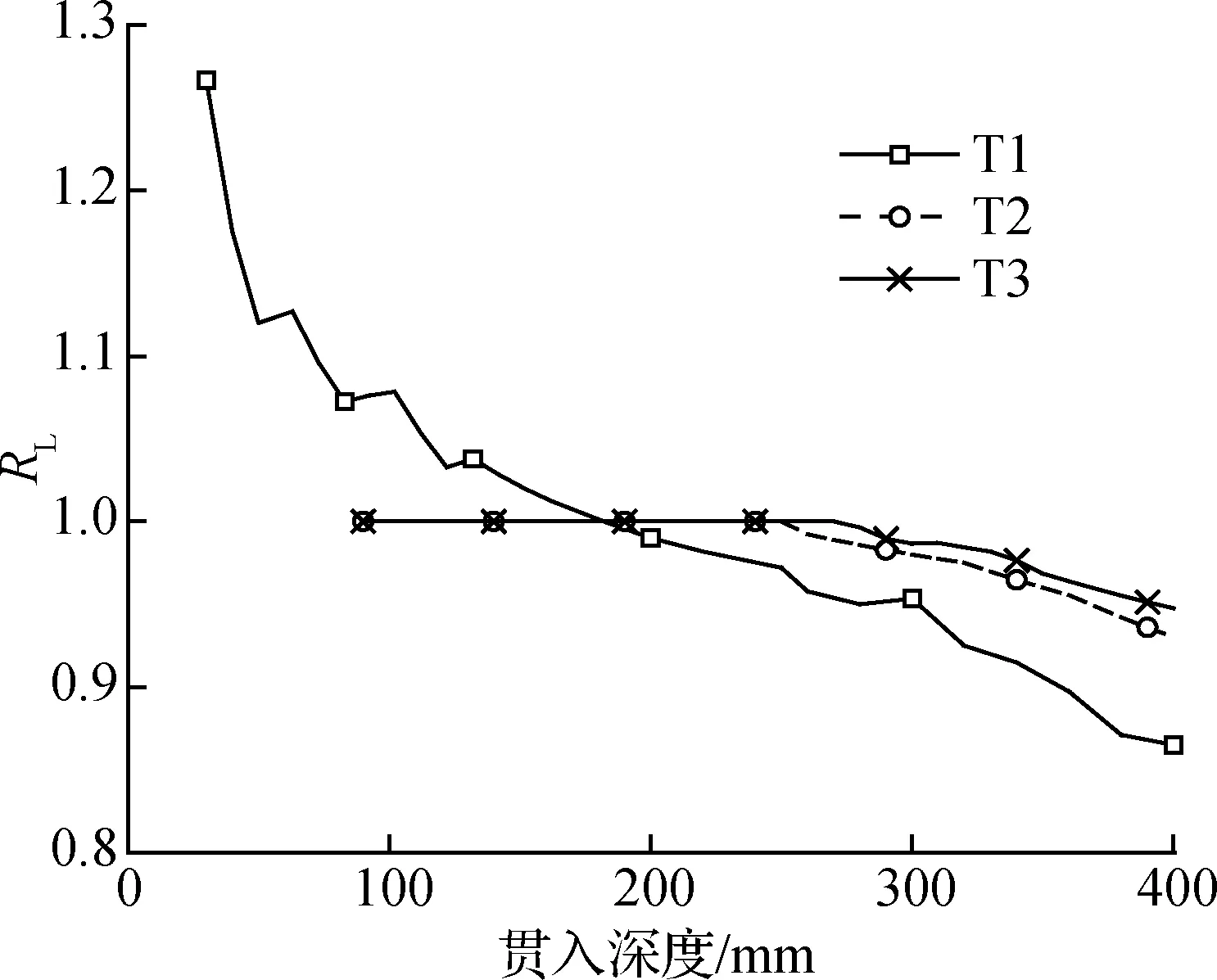
(a) 沉贯过程中土塞率变化
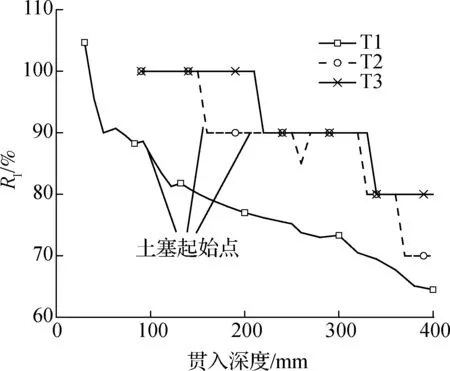
(b) 土塞增长率曲线图12 土塞长度变化曲线
结合图10可知,T2,T3的贯入阻力大小接近,这与图12(b)中T2,T3土塞闭塞程度相吻合;对比分析工况T2,T3的土塞率在290 mm深度处出现闭塞现象与土塞增长率在200 mm深度处出现闭塞现象对土塞闭塞程度判断可知,在口径较大、土塞长度无明显变化时,将土塞率作为判断闭塞程度的判据,其结果误差较大.
4 结论
1) 在砂土中,筒型基础下沉过程中筒体内壁土压力与贯入力的增长趋势相同,增长速度随深度而增加,而外壁土压力成线性趋势增大,更接近极限被动土压力值,可用折减的被动土压力进行计算.
2) 土塞闭塞程度随筒体口径增大而降低,土拱阻力在沉贯过程中占贯入总阻力的比例成增大的趋势,是沉贯阻力的重要组成部分,且土拱被挤压进筒体内部是导致筒内土压力增大的原因之一.
3) 沉贯深度达到1倍口径深度时开始出现土塞现象,工况T1,T2,T3中沉贯结束时土塞增长率分别为65%,70%,80%,表明土塞闭塞程度随口径的增大而减轻.
4) 基于土拱效应理论建立了筒内壁土压力计算公式,建立了考虑桶内土塞作用的贯入力预测计算方法,对比发现理论计算结果与静压下沉试验数据吻合较好.
参考文献(References)
[1] Andersen K H, Jostad H P, Dyvik R. Penetration resistance of offshore skirted foundations and anchors in dense sand[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2008,134(1):106-116. DOI:10.1061/(asce)1090-0241(2008)134:1(106).
[2] 陈飞. 砂土中海上风机筒型基础沉放过程筒-土作用研究[D]. 天津:天津大学建筑工程学院,2014.
[3] 刘润, 祁越, 练继建. 无黏性土中筒型基础静压下沉模型试验研究[J]. 水利学报, 2016, 47(12):1473-1483. DOI:10.13243/j.cnki.slxb.20160262.
Liu Run, Qi Yue, Lian Jijian. Experimental study on static pressure penetration of bucket foundation in cohesionless soil[J].JournalofHydraulicEngineering, 2016,47(12):1473-1483. DOI:10.13243/j.cnki.slxb.20160262. (in Chinese)
[4] 霍知亮. 黏土地基中桶形基础模型试验及工作机理研究[D]. 天津:天津大学建筑工程学院,2015.
[5] 闫澍旺, 林澍, 霍知亮,等. 桶形基础液压下沉过程的耦合欧拉-拉格朗日有限元法分析[J]. 岩土力学, 2017,38(1):247-252. DOI:10.16285/j.rsm.2017.01.031.
Yan Shuwang, Lin Shu, Huo Zhiliang, et al. Coupled Eulerian-Lagraangian finite element analysis of suction caisson penetration processed under hydraulic pressure[J].RockandSoilMechanics, 2017,38(1):247-252. DOI:10.16285/j.rsm.2017.01.031 .(in Chinese)
[6] 杨旭, 陈飞, 练继建,等. 考虑挤土效应的筒型基础沉放阻力数值分析及试验验证[J]. 岩土力学, 2014, 35(12):3585-3591. DOI:10.16285/j.rsm.2014.12.035.
Yang Xu, Chen Fei, Lian Jijian, et al. Numerical analysis and test verification of penetration resistance for bucket foundation installation considering effect of soil squeezing[J].RockandSoilMechanics, 2014,35(12):3585-3591. DOI:10.16285/j.rsm.2014.12.035 .(in Chinese)
[7] 李大勇, 吴宇旗, 张雨坤. 砂土中吸力式桶形基础竖向承载性状研究[J]. 山东科技大学学报(自然科学版), 2016, 35(3):33-39. DOI:10.16452/j.cnki.sdkjzk.2016.03.019.
Li Dayong, Wu Yuqi, Zhang Yukun. Vertical bearing capacity of suction caisson foundation in sand[J].JournalofShandongUniversityofScienceandTechnology(NaturalScience), 2016,35(3):33-39. DOI:10.16452/j.cnki.sdkjzk.2016.03.019. (in Chinese)
[8] Randolph M F. Science and empiricism in pile foundation design[J].Géotechnique, 2003,53(10):847-875. DOI:10.1680/geot.53.10.847.37518.
[9] 贾海莉, 王成华, 李江洪. 关于土拱效应的几个问题[J]. 西南交通大学学报, 2003, 38(4):398-402.
Jia Haili, Wang Chenghua, Li Jianghong. Discussion on some issues in theory of soil arch[J].JournalofSouthwestJiaotongUniversity, 2003,38(4):398-402. (in Chinese)
[10] 胡永强, 汤连生, 李兆源. 静压桩桩-土界面滑动摩擦机制研究[J]. 岩土力学, 2015, 36(5):1288-1294. DOI:10.16285/j.rsm.2015.05.007.
Hu Yongqiang, Tang Liansheng, Li Zhaoyuan. Mechanism of sliding friction at pile-soil interface of jacked pile[J].RockandSoilMechanics, 2015,36(5):1288-1294. DOI:10.16285/j.rsm.2015.05.007 .(in Chinese)
[11] Terzaghi K. 理论土力学[M]. 徐志英,译.北京: 地质出版社, 1960:151-153.
[12] 王旭东, 梅国雄, 宰金珉. 被动土压力折减系数的研究[J]. 工业建筑, 2003, 33(1):29-31.
Wang Xudong, Mei Guoxiong, Zai Jinmin. The study on reductied coefficient of passive earth pressure[J].IndustrialConstruction, 2003,33(1):29-31. (in Chinese)
[13] 刘建航, 侯学渊. 基坑工程手册[M]. 北京:中国建筑工业出版社, 1997:247-248.
[14] 黄生根, 冯英涛, 徐学连,等. 考虑土塞效应时开口管桩的挤土效应分析[J]. 沈阳工业大学学报, 2015, 37(5):582-587.
Huang Shenggen, Feng Yingtao, Xu Xuelian, et al. Analysis on squeezing effect of open-ended pipe pile with considering plugging effect[J].JournalofShengyangUniversityofTechnology, 2015,37(5):582-587. (in Chinese)
