“数形结合”在一次函数与一元一次方程、一元一次不等式中的应用
2018-06-09黄慧姬
◎黄慧姬
一、“数形结合”的内涵及重要性
“数形结合”是一个重要的数学思想方法,它应用大致分为两种情形:(1)“以数解形”借助于数的精确性、规范性、严密性来阐明形的一些属性(2)“以形助数”借助形的直观性、生动性来阐明数与数之间的联系。所谓数形结合,就是根据数与形之间的对应关系,通过数与形之间的相互转化来解决数学问题的一种重要思想方法。
我国著名的数学家华罗庚就说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休。”道出了“数形结合”思想的重要性及重大意义。“数形结合”既是一种重要的数学思想也是一种常用的数学方法。数形结合在数学解题中有着重要的指导意义,这种“数”与“形”的信息转换,相互渗透,不仅可以使一些题目化繁为简、化难为易、化抽象为直观,同时还可以开拓解题思路、提高解题能力,为解决数学问题开辟了一条重要的途径。又特别是对抽象的、复杂的函数问题,一定要学会用“数形结合”的思想来解决。
二、“数形结合”在一次函数与一元一次方程的应用
1.一次函数与一元一次方程的关系 一次函数与一元一次方程有着密切的联系。求一元一次方程kx+b=0(k,b是常数,k≠0)的解,从“数”的方面看:转化为一次函数就是求函数y=kx+b,当y=0时,X的值;从“形”的方面看:就是求直线y=kx+b与X轴交点的横坐标。
可是数学概念的形成是很抽象的、很难理解的,又特别是对于刚刚接触函数内容的初中学生来说,像以上的概念根本无法理解。所以作为老师的我们就应该寻找方法把抽象的问题直观化、把复杂的问题简单化,其中“数形结合”的方法就是一种很不错的选择。
例如:我通过以下问题的设计,让学生通过问题利用“数形结合”的方法能够真正的理解一次函数与一元一次方程之间的密切关系:
(1)方程2x-4=0的解是
(2)函数 y=2x-4中,当 y=0时,x=
(3)画出函数y=2x-4图象,图象与x轴的交点坐标是__________:
你有什么发现?
2.“数形结合”在解题中的渗透 数学研究的对象是数量关系与几何图形,数和形既是对立的又是统一的,并且在一定条件下可以相互转化,综合运用。数量关系可以通过图形直观的表示出来,然后应用几何图形的知识解答有关代数的问题;另一方面,有关图形的性质也可通过数量关系来计算和描述,从而达到利用代数的方法来解决几何的问题。例:某种摩托车的油箱最多可储油10升,加满后,油箱中的剩油量y(升)?与摩托车行驶路程x(千米)之间的关系式如图所示。

根据图象所提供的信息,回答下列问题:
(1)一箱汽油可供摩托车行驶多少千米?
(2)摩托车每行驶100千米消耗多少升汽油?
(3)油箱中的剩余油量小于1升时,摩托车将自动报警,行驶多少千米后,摩托车将自动报警。
三、“数形结合”在一次函数与一元一次不等式的应用
1.一次函数与一元一次方程的关系 求ax+b>0(或<0)(a,b是常数,a≠0)的解集,从“数”的方面看:转化为一次函数就是函数y=ax+b的函数值大于0(或小于0)时x的取值范围;从“形”的方面看:直线y=ax+b在X轴上方(或下方)时自变量的取值范围。
在这个内容中,学生考试失分率很高,主要的原因是学生不会把函数关系式或函数图象与一元一次不等式联系起来。为了解决这个问题,我们应该充分的利用多媒体的辅助教学,制作微视频,直观地呈现教学素材,让枯燥的理论知识直观化、形象化、生动化,训练学生利用数形结合的思想解决问题,从而提高学生的理解能力和思维能力,激发学生的学习积极性。
2.“数形结合”在解题中的渗透 例:如图是一次函数y=kx+b(k≠0)的图象,
(1)则关于x的不等式kx+b>0的解集为_________;
(2)则关于x的不等式kx+b<0的解集为__________;
(3)当0<x≤2时,y的取值范围为 。
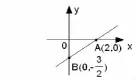
分析:这个问题可以有两种解决方法(1)从“数”的角度去解决:由图形可以知道一次函数图像都经过A、B两点,所以可以通过A、B两点的坐标先求出一次函数的解析式,再解相关不等式的解集。但这种方法需要的计算量及时间比较大,而且对第三题的解题过程又容易出错。(2)从“形”的角度去解决:不用计算,观察图形由A、B两点的坐标可以直接得出所有的问题的答案,显然第二种方法比较省时省事。但是不管是哪一种方法都必须把“数”与“形”有机结合起来才能解决问题。因此“数形结合”是一种很重要的数学思想,它渗透在数学教学中的每个知识点。但学生对于这种思想的掌握又很困难,在解题中作为数学老师要做好这种“数”与“形”关系的揭示与转化,引导学生认识问题中的实质——数学知识的精髓,不断地去引导学生将“数”转化为“形”,同时还能够将“形”转化为“数”,并能把“数”与“形”有机的综合起来灵活应用,最终才能将知识转化为自己内化的东西,形成能力。
