巧用斜率求参数的范围

◎朱帅

例1：［2014·山东理20］设函数（k为常数，e=2.718 28…是自然对数的底数）.

（1）当 k≤0时，求函数 f（x）的单调区间；

（2）若函数 f（x）在（0，2）内存在两个极值点，求 k的取值范围.

解析：本题问题（2）要求k的取值范围，我们可以用斜率来解决问题：

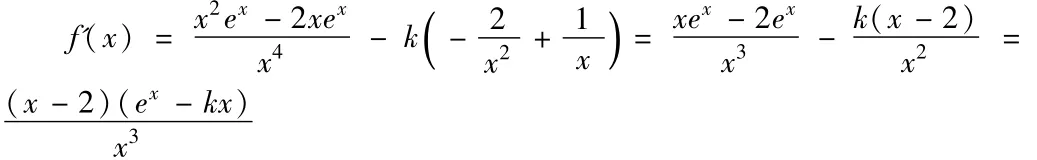
若函数 f（x）在（0，2）内存在两个极值点，则方程 f′（x）=0在（0，2）内有两个不相等的实数根，∵x∈（0，2），∴x3＞0，x-2＜0，所以f′（x）=0等价于ex-kx=0，

从而方程ex-kx=0在（0，2）内有两个不相等的实数根。∴表示函数y=ex在x∈（0，2）内图像上的点P（x，ex）与坐标原点O（0，0）的连线l的斜率，由图（1）知，l介于切线l1与割线l2之间，从而k介于切线k1与割线k2之间.

设切点为 （x0，y0），则 y′=ex，所以 k1=ex0，

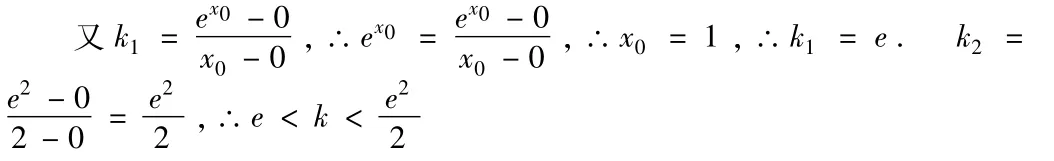
例2：［2016·广州二模理21］已知函数 f（x）=e-x-ax（x∈ R）.

（Ⅰ）当a=-1时，求函数f（x）的最小值；

（Ⅱ）若x≥0时，f（-x）+ln（x+1）≥1，求实数a的取值范围；

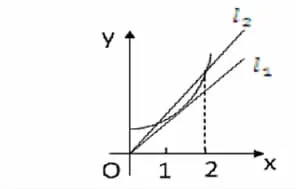
（Ⅲ）求证：.

解析：本题问题（2）求a的取值范围，我们可以用斜率来解决问题：

依题意，x≥0时，即 f（-x）+ln（x+1）≥1即 ex+ax+ln（x+1）-1≥0.

∴ ax≥1-ex-ln（x+1）

当x=0时，上式恒成立，此时a∈R

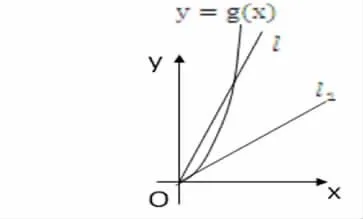
令，则k表示函数

g（x）=ex+ln（x+1）-1图像上的点

P（x，ex+ln（x+1）-1）（x∈（0，+∞））与坐标原点O（0，0）的连线l的斜率，由图（2）知，l介于切线 l1与 y轴之间，因为 g′（x）=ex+，∴函数g（x）在（0，+∞）递增且递增速度越来越快，又g（x）过原点 O（0，0），∴ k＞g′（0） =2，即，

从而a≥-2，综上所述，a∈［-2，+∞）

例3：［2016·湛江一模理21］设函数 f（x）=（ax+1）e-x（a∈ R）.

（I）当 a＞0时，求 f（x）的单调递增区间；

（II）对任意 x∈［0，+∞），f（x）≤x+1恒成立，求实数 a的取值范围

解析：本题问题（2）求a的取值范围，我们可以用斜率来解决问题：

f（x）=（ax+1）e-x≤x+1恒成立，x∈［0，+∞）

当x=0时，上式恒成立，此时a∈R

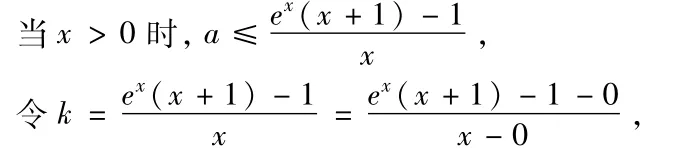
则 k表示函数g（x）=ex（x+1）-1图像上的点P（x，ex（x+1）-1）（x∈（0，+∞））与坐标原点 O（0，0）的连线l的斜率，由图（3）知，l介于切线 l1与 y轴之间。因为 g′（x）=（x+2）ex，∴函数 g（x）在 （0，+∞）递增且递增速度越来越快，又g（x）过原点O（0，0），∴ k＞g′（0）=2，即，从而a≤2，综上所述，a∈（-∞，2］

点评：例1—例3中解法，不仅省去了复杂的计算过程，而且它的原理更贴近初等数学，学生也非常容易掌握.在高中数学中，有关函数的证明题，学生大都会首先想到构造函数，通过求导判断函数的单调性来证明.经过多年的解题训练，很多学生都形成了惯性思维，很难再有新的突破.但如果我们认真观察，用心去想，很多问题是可以跳出惯性的约束，另外一种再平凡不过的方法或许会让我们柳暗花明.特别是高等数学的方法用之于初等数学时，一定要抓住实质.导数离散化之后就是斜率，从这个意义上讲，斜率更具有根本意义，而且在高中数学中斜率还是一个核心概念.

构造斜率只是解决恒成立问题中求参数的取值范围的一种方法，并非适用于所有的问题，但是如果条件适合，构造斜率往往能让我们变抽象为直观，减少分类讨论的麻烦，甚至简化许多繁琐的计算，达到事半功倍的效果。

［1］ 刘有良.构造解析几何模型解代数问题［J］.数学教学通讯.2002，11（下），50-51.