数学思维与小学数学教学

◎付凤英

有的家长会说：“老师，我家孩子平时学习挺努力的，上课认真听讲了，做作业也挺认真的，但是就是学不好，成绩上不去。”其实要学好数学，最重要的是讲究思维方法。家长和老师要做的就是帮孩子练好基本功，适当的培养孩子的数学思维方式，对将来的学习是有很大的帮助的。那么，什么是数学思维呢？

数学思维就是数学地思考问题和解决问题的思维活动形式。思维指的是人脑对客观现实的概括和间接反映，属于人脑的基本活动形式。数学思维也就是人们通常所指的数学思维能力，即能够用数学的观点去思考问题和解决问题的能力。比如转化与划归，从一般到特殊、特殊到一般。数学基础的本质就是两样东西：概念和应用，通俗的说就是“定义”和“公式”，要把这两样东西搞懂搞透。在此，我们来谈谈四种常用的数学思维在小学数学教学中的体现和应用。

一、对应思维

对应思维包含一般对应和量率对应等内容，一般对应是从一一对应开始的。例：

小红有7个三角，小明有5个三角，小红比小明多几个三角？

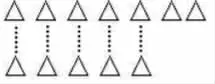
这里的虚线表示的就是一一对应，即：同样多的5个三角，而没有虚线的2个，正是小红比小明多的三角。

二、假设思维

1、假设是针对一定的问题，我们根据自己的经验、直觉（要信任自己的直觉，因为直觉从某种意义上来说，是你知识积累的一种体现）或头脑风暴后先给出一系列答案。这些答案是我们在没有进行实际研究的情况下给出的解决问题的方案，称之为假设。例：有两块布共长7.66米，第一块比第二块长1/5还多0.4米，这两块布各长多少米？

解答这道题就需要假设思维方法的参予。如果没有这种思维方法，将难以找到解题思路的突破口。题目中有两数的“和”。而且是直接条件，两数的“倍”不仅是间接条件，并且附加着“还”多0.4米的条件，这是一道较复杂的和倍应用题，思考这道题，必须进行如下的假设。如果第一块比第二块就长1/5，而不多0.4米，那么从两块布共长的7.66米中减去0.4米，这时所得的差（7.56米）与两块布的倍数和［倍］，是直接对应的，至此，就完全转化成简单的和倍应用题。根据题意，其倍数关系如图：

答：第一块4.36米，第二块3.3米。

2、唐朝的时候，唐太宗为了“和蕃”，将文成公主下嫁吐蕃王松赞干布，这是历史上的美谈。

据说在决定嫁出文成公主之前，曾有来自各地的4位少数民族使者，请求唐太宗将文成公主嫁给他们的国君。唐太宗十分为难，为求公平，他出了5道难题让各国使者来比赛，哪国使者赢了，公主就嫁给该国国君。吐蕃王松赞干布的使者禄东赞也是其中的一个使者。

有两道难题是这样的：

第一题，太监拿来一颗孔内有9道弯的“九曲明珠”，让大家分别用一根很细的丝线穿过去。各位使者不停地用手去穿线，丝线一直穿不过去。这时只见禄东赞找人捉来了一只大蚂蚁，将丝线轻轻拴在蚂蚁身上放人孔内，而在另一个孔端抹上一些蜜糖。很快地，蚂蚁就由这一端爬到另一端，而将丝线也带了出去。

第二题，马厮的两边各关100匹母马和100匹小马。太监要使者们轮流辨认出每匹小马的妈妈。

使者们将栅栏打开，让小马到母马堆里，认为小马总是对母马会比较亲近。但是，事实并不如此，因为母马看也不看小马一眼，小马也自顾自地玩耍。许多使者只好根据马身上的花纹随便乱猜乱配。

最后轮到禄东赞来辨马时，他要仆役将小马关上一天，并且不给水喝。第二天仆役打开了栅栏，渴极了的小马纷纷奔向自己的妈妈找奶吃，于是，禄东赞轻而易举地辨认出了小马的妈妈。

就这样，聪明的禄东赞为他年轻的吐蕃国君松赞干布娶回了文成公主。

禄东赞的聪明在于，他是先假定问题是可以解开的。

首先，第一题中，他假定丝线会像眼睛似地走过9道弯，顺利地由另一端出去，于是再动脑筋想什么东西可以钻过小孔，又长眼睛？又怎么引诱它走出去？然后就想到了蚂蚁，以及用蜜糖来引诱蚂蚁。

第二题中，他假定小马都会自动奔向母马，用什么方法去诱导它们呢？当然是小马的天性，即吃奶！这种假设思考帮助禄东赞由结果往前推理，从而顺利地解开了难题。

三、转化思维

经过转化后的数量关系，就由复杂转化为简单，由隐蔽转化为明显，为正确解题思路的形成，创造了必要的条件。例：有一批货物，甲车运走全部的，乙车运的是甲车的，丙车运的是乙车的，这批货物还剩下几分之几？

从题意中可知，求这批货物还剩下几分之几，必须先知道三辆车共运走全部的几分之几，全部看作标准量“1”，但条件中的标准量却有三个，“全部”、“甲车”和“乙车”，如果不把“甲车”和“乙车”这两个标准量，也统一成“全部”这个标准量，正确的思路将无法形成。

由于甲车运走全部的，乙车运的是甲车的所以乙车运的就是全部的；根据乙车运的是全部的，丙车运的又是乙车的，丙车运的必然是全部的，至此标准量经过两次转化，已经全部统一。列式计算为：

四、小结

“数学思维”这些原本听上去高不可攀的词，其实它就渗透在我们的数学教学过程中，并不是遥不可及，我们的学生经过我们的教学能够“学会数学地思维”，能用数学思维解决实际问题，举一反三，达到教学目的。

［1］小学数学思维培养策略略谈［J］.张家宏.新课程学习（中）.2014（07）

［2］浅议小学数学教学中的数学思维培养［J］.张正周.科技致富向导.2013

［3］小学生数学思维培养的问题及策略［J］.肖琼.学生之友.2013（04）