基于局部搜索OMP的网格失配STAP算法

李志汇, 张永顺,2, 高 乾, 郭艺夺, 王 强, 刘 洋

(1. 空军工程大学防空反导学院, 陕西 西安 710051; 2. 信息感知技术协同创新中心, 陕西 西安 710077;3. 空军通信士官学校, 辽宁 大连 116600)

0 引 言

机载雷达在进行地面/海面弱小目标检测时,面临的强地/海杂波往往将微弱目标淹没,严重影响了运动目标的检测性能。空时自适应处理(space-time adaptive processing, STAP)对空时二维回波数据进行联合处理,能够有效地将杂波和目标在空时二维域中分离开来[1-2],显著提升了机载雷达对慢速目标的检测性能。STAP技术通常需要足够多的独立同分布(independent identically distributed, IID)训练样本来估计杂波协方差矩阵,然而在实际环境中,样本非均匀导致难以获得足够多的IID样本,从而导致STAP的性能严重下降[3]。近年来,不少学者将稀疏恢复(sparse recovery, SR)技术引入到STAP中,认为杂波在整个空时二维平面的分布是稀疏的[4],首先采用SR算法恢复出杂波的空时谱,然后采用恢复出的空时谱来构造杂波协方差矩阵,进而计算STAP权矢量,这类方法被称为SR-STAP技术[5-8]。SR-STAP技术在不需要杂波先验信息的情况下,使用非常少量的训练样本就能够估计比较准确的杂波协方差矩阵。SR-STAP技术在构建STAP完备字典时一般假定离散化后的空时网格点与杂波脊完全对准,然而实际情况下,杂波散射点并不是恰好落在离散化的空时网格点上,从而导致杂波协方差矩阵的估计精度严重下降,这就是网格失配STAP问题,也可称为基失配STAP问题。

当前,国内外众多学者针对网格失配问题的研究,提出了许多有效的算法。文献[9]指出存在网格失配时,SR算法的性能将严重下降。一种比较直接的方法是增加网格的数量来解决网格失配问题,但是网格数过于密集将会导致邻近导向矢量比较高的相关性,另外将会导致计算复杂度显著增加。文献[10]提出了一种扰动正交匹配追踪(perturbed orthogonal matching pursuit, POMP)的算法解决基失配问题,该方法能够显著降低重构误差。针对波达方向(direction of arrival,DOA)估计中的网格失配问题[11-14],文献[11]提出了一种稀疏贝叶斯参考(sparse Bayesian inference, SBI)算法,该算法首先建立了一阶泰勒级数展开模型,然后从贝叶斯参考的角度,利用信号的拉普拉斯先验提出了SBI算法来解决所建立的模型。文献[12]建立了包含误差参数的稀疏恢复DOA估计模型,提出了一种扰动稀疏贝叶斯学习(perturbed sparse Bayesian learning, PSBL)算法来解决网格失配问题。针对压缩感知成像存在网格失配问题,文献[15]提出一种基于贝叶斯压缩感知的稀疏自聚焦(SAF-BCS)成像算法,该方法采用变分贝叶斯学习技术求解包含网格失配目标的稀疏像。文献[16]从原子范数出发,综述了无网格压缩感知的理论框架和关键技术。虽然针对网格失配的问题研究较多,但是上述研究成果不能直接应用于网格失配STAP问题。针对网格失配STAP问题,文献[17]采用字典学习方法来寻找最优基矩阵,提出了压缩感知字典学习(CSDL)的方法,但是该方法仅适用于杂波线性分布于空时平面的情形。文献[18]提出一种参数搜索正交匹配追踪(orthogonal matching pursuit, OMP)的算法来解决SR-STAP中的基失配问题,该方法通过搜索最优参数来寻找与真实导向矢量相匹配的原子,但是该方法在每次迭代过程中都要采用梯度下降算法求解最优参数。

针对网格失配STAP问题,本文提出一种基于局部搜索(local search,LS)OMP STAP算法,称为LS-OMP-STAP算法。该算法首先从全局STAP完备字典中选择与杂波信号相匹配的全局网格点;然后以选出的全局网格点为中心,构建局部STAP完备字典,并从中选择与杂波信号最匹配的局部网格点,进而获得杂波的角度-多普勒像和修正的STAP字典,并用它们计算杂波的协方差矩阵。该算法能够显著降低网格失配带来的STAP性能损失。

1 信号模型

1.1 杂波信号模型

图1 机载雷达阵列几何关系图Fig.1 Illustration of airborne radar array geometry

不考虑距离模糊,则一个距离门雷达接收的杂波加噪声数据(称作空时快拍数据)可以表示为

(1)

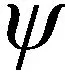
v(fdi,fsi)=vd(fdi)⊗vs(fsi)

(2)

式中,⊗表示Kronecker积;vd(fdi)和vs(fsi)分别表示时域导向矢量和空域导向矢量,可以表示为

vd(fdi)=[1,exp(j2πfdi),…,exp(j2π(K-1)fdi)]T

(3)

vs(fsi)=[1,exp(j2πfsi),…,exp(j2π(N-1)fsi)]T

(4)

将空时二维平面离散化为Ns×Nd个网格点,其中,Ns=ρsN,Nd=ρdK,并且ρs,ρd>1。则离散化空域频率间隔和离散化时域频率间隔可以分别表示为Δfs=1/Ns和Δfd=1/Nd。每个网格点对应一个空时导向矢量,假定所有的杂波散射块都恰好落在离散化的空时网格点上,则式(1)可以表示为

x=Φγ+n

(5)

式中,Φ∈CNK×NsNd为STAP完备字典,由所有网格点对应的空时导向矢量构成,可以表示为

Φ=[v(fd1,fs1),v(fd1,fs2),…,v(fdNd,fsNs)]

(6)

γ=[γ1,1,γ1,2,…,γNd,Ns]T表示杂波的角度-多普勒像,其中的非零元素表示杂波块在空时二维平面的位置。

1.2 网格失配STAP

实际情况下,在构造STAP完备字典时,并不能保证杂波散射块恰好落在离散化的网格点上。因此,存在着网格失配问题。图2给出了网格失配STAP的示意图,整个空时二维平面离散化为很多细小的网格,每个网格点对应于一个空时导向矢量,所有的网格点对应的空时导向矢量构成了STAP完备字典。从图2中可以看出,杂波脊并不能与网格点完全重合,即存在网格失配问题,利用存在失配的STAP完备字典恢复得到的杂波块的位置和幅度存在偏差,进而导致所构造的杂波协方差矩阵与真实的杂波协方差矩阵存在偏差,从而影响SR-STAP技术的杂波抑制性能。

图2 网格失配STAP示意图Fig.2 Illustration of off-grid STAP

2 LS-OMP-STAP算法

2.1 LS-OMP-STAP算法的思想

LS-OMP-STAP算法的具体思路是:首先按照常规方式构造一个全局STAP字典ΦG(构造该字典时可以不用采用非常密集的网格),并在OMP算法的每次迭代中,挑选得到一个全局网格点,如图3中红色大圆点所示;然后再根据这个全局网格点的位置信息构造一个局部STAP字典ΦL(以挑选的全局网格点为中心,以离散化空域频率间隔Δfs和时域频率间隔Δfd为宽度设计大小为NL,s×NL,d的局部STAP字典,得到Q=NL,sNL,d个局部网格点,如图3中蓝色小圆点所示);最后,在该局部字典上再进行一次挑选,挑选出的局部网格点能够与杂波块更匹配,并用其修正全局STAP字典,进而得到杂波的角度多普勒像,并用获得的更新后的STAP全局字典和杂波角度多普勒像来计算杂波加噪声协方差矩阵。

图3 局部STAP字典设计示意图Fig.3 Illustration of the design of local STAP dictionary

2.2 LS-OMP-STAP算法步骤

LS-OMP-STAP算法具体步骤如下:

输入

全局STAP字典ΦG=[vG,1,vG,2,…,vG,P],其中P=NsNd,空时快拍数据x,局部STAP字典的大小Q,迭代终止限度σ或迭代次数K。

初始化

迭代

步骤1依据下式从ΦG中寻找与rk-1最相关的原子的索引,即

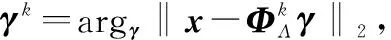
步骤5当‖rk‖2<σ或者k≤K时迭代终止,否则,k=k+1,转到步骤1。

输出

(7)

式中,(·)H表示共轭转置;β为对角加载系数。

2.3 计算复杂度分析

LS-OMP-STAP算法的计算复杂度主要在步骤1,步骤2和步骤4。在第k次迭代中,步骤1需要的浮点操作次数(floating point operations, flops)为(2M-1)P,其中M=NK表示系统自由度;步骤2需要的flops次数为(2M-1)Q;步骤4计算杂波的角度-多普勒像,采用最小二乘法需要的flops次数为4kM,余量更新需要的flops次数为2kM[19]。假定算法迭代了T次数,则LS-OMP-STAP算法总的flops次数约为2M(P+Q)T+3MT2。同理,OMP-STAP算法与LS-OMP-STAP算法相比少了局部搜索步骤,即步骤2,当迭代次数为T时,OMP-STAP算法所需的总的flops次数为2MPT+3MT2。

3 仿真实验分析

本节通过仿真试验来证明本文的LS-OMP-STAP算法的有效性,机载正侧视ULA的仿真参数如表1所示。

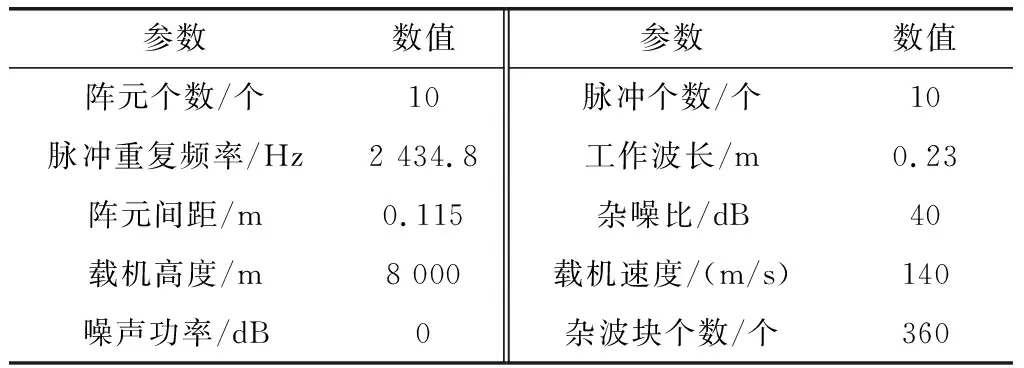
表1 机载ULA系统参数

图4分别给出了随机一次仿真中OMP-STAP算法和LS-OMP-STAP算法所挑选出的原子在空时二维平面的位置分布情况。其中OMP算法使用的STAP完备字典设置为ρs=4,ρd=4;LS-OMP-STAP算法使用的全局STAP字典设置为ρs=4,ρd=4,局部STAP字典大小设置为NL,s=10,NL,d=10。实验中两种算法都选取一个空时快拍数据,且迭代次数设定为K=19。从图4中可以看出OMP-STAP算法挑选出的原子与杂波脊存在严重偏离,而LS-OMP-STAP算法挑选出的原子则与杂波脊距离非常接近。这是因为OMP-STAP算法使用的STAP完备字典存在比较严重的网格失配,而LS-OMP-STAP算法由于增加了局部搜索步骤,能够在更精细的网格上搜索与杂波脊匹配的原子。需要说明的是,虽然图4的结果仅是一次仿真所得,但该结论适用于任何一次仿真实验。

图4 两种算法挑选出的原子位置分布Fig.4 Location distribution of selected atoms for different algorithms

图5(a)给出了理想情况下LS-OMP-STAP算法与两种OMP-STAP算法的改善因子对比图。图5(b)给出了阵元误差为5%情况下的改善因子对比图。图5中的结果通过200次蒙特卡罗仿真实验得到,OMP1-STAP算法使用的STAP完备字典设置为ρs=4,ρd=4,OMP2-STAP算法使用的STAP完备字典设置为ρs=6,ρd=6。仿真实验中所有算法都采用4个空时快拍数据,其他参数设置同上。从图5(a)可以看出,3种算法在旁瓣杂波区的改善因子性能相近,但是在主瓣杂波区,OMP1-STAP和OMP2-STAP算法的改善因子的凹口展宽十分严重,而LS-OMP-STAP算法相比较来说凹口展宽较小。从图5(b)可以看出,所有算法的性能在存在阵元误差时都有所下降,在旁瓣杂波区,LS-OMP-STAP算法的性能跟OMP1-STAP和OMP2-STAP算法相比有所下降,但在主瓣杂波区,LS-OMP-STAP算法的性能仍然比OMP1-STAP和OMP2-STAP算法较好。说明LS-OMP-STAP算法增加的局部搜索步骤能够在一定程度上降低网格失配带来的性能损失。

图6为所有算法的平均改善因子与空时快拍数的关系曲线。图6(a)为理想情况下的仿真结果,图6(b)为阵元误差为5%时的仿真结果。其中平均改善因子定义为在整个归一化多普勒频率上改善因子的平均值,图中结果经过了200次蒙特卡罗仿真实验得到。从图6(a)可以看出,随着样本数的增加,所有算法的平均改善因子性能稍微有所下降,这是由于杂波凹口稍微有所变宽导致的,通过对比可以看出,LS-OMP-STAP算法的平均改善因子要高于OMP1-STAP和OMP2-STAP算法。从图6(b)中可以看出,存在阵元误差时所有算法的平均改善因子都有一定程度的下降,其中LS-OMP-STAP算法的平均改善因子要优于OMP2-STAP算法,但其在样本数少于12时则比OMP1-STAP算法较差,样本数高于12时比OMP1-STAP算法较好。这进一步说明了LS-OMP-STAP算法能够提升稀疏恢复STAP的性能,在理想条件下改善效果更加明显。

在上述理想情况仿真条件下,通过分析可以得到LS-OMP-STAP算法所需总的flops次数约6 568 300,OMP1-STAP算法约为6 188 300,OMP2-STAP算法约为13 788 300。表2表示3种不同算法计算一次杂波角度-多普勒像的平均计算时间,所有的结果经过200次蒙特卡罗仿真实验获得,仿真实验平台在标准台式计算机上完成,平台参数为3.60 GHz I7-4790 CPU,内存为8 GB。从表2可以看出,LS-OMP-STAP算法的平均计算时间要比OMP1-STAP算法较大,而比OMP2-STAP算法的平均计算时间相对较小。说明LS-OMP-STAP算法在计算复杂度相对较低的同时能够获得较优的STAP性能。

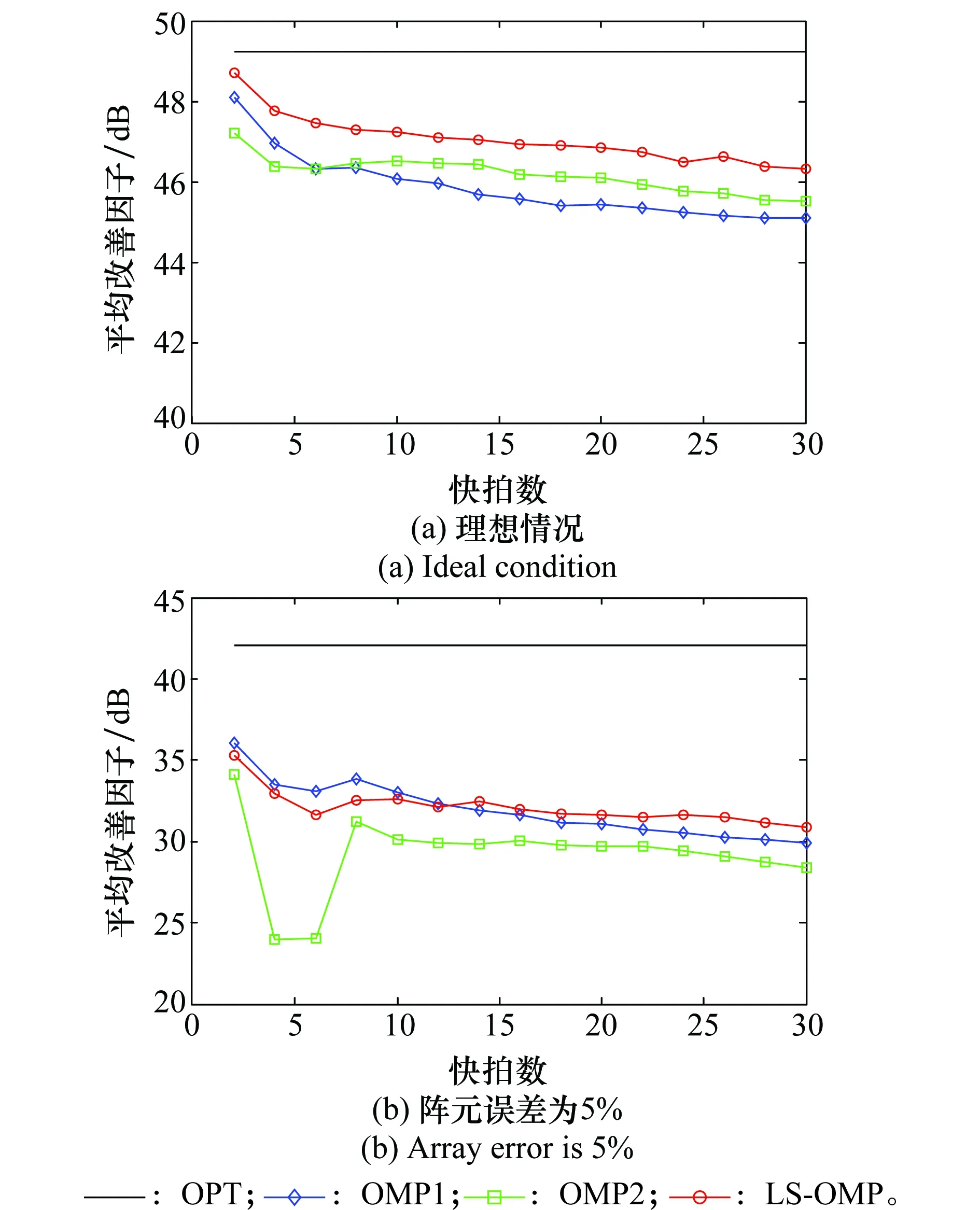
图6 不同算法的平均改善因子随快拍数的变化Fig.6 Average IF of different algorithms against the snapshots

算法OMP1OMP2LS-OMP平均计算时间/s0.056 60.142 70.132 9

4 结 论

针对稀疏恢复STAP算法网格失配造成STAP性能下降的问题,本文提出了一种基于OMP算法的LS-OMP-STAP算法,该算法对OMP算法进行改进,增加了局部搜索步骤来选择与杂波脊更匹配的原子来估计杂波的角度-多普勒像,避开了简单的增加网格密度带来的计算复杂度增加的问题。仿真实验证明了本文所提的算法能够选择与杂波脊更接近的原子,明显降低网格失配所带来了STAP性能下降的问题,并且计算复杂度也相对较低。

参考文献：

[1] WARD J. Space-time adaptive processing for airborne radar[R]. Technical Report 1015, Massachusetts: MIT Lincoln Laboratory, 1994.

[2] KLEMN R. Principles of sparse-time adaptive processing[M]. London: Institute of Electrical Engineering, 2006.

[3] MELVIN W L. Space-time adaptive radar performance in heterogeneous clutter[J]. IEEE Trans.on Aerospace and Electronic Systems, 2000, 36 (2):621-633.

[4] YANG Z C, LI X, WANG H Q, et al. On clutter sparsity analysis in space-time adaptive processing airborne radar[J]. IEEE Geoscience Remote Sensing Letters, 2013, 10 (5): 1214-1218.

[5] SUN K, MENG H D, WANG Y, et al. Direct data domain STAP using sparse representation of clutter spectrum[J]. Signal Processing, 2011, 91 (9): 2222-2236.

[6] SUN K, MENG H D, LAPIERRE F D, et al. Registration-based compensation using sparse representation in conformal-array STAP[J]. Signal Processing. 2011, 91 (10) : 2268-2276.

[7] SEN S. Low-rank matrix decomposition and spatio-temporal sparse recovery for STAP radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9 (8): 1510-1523.

[8] WANG Z T, XIE W C, DUAN K Q, et al. Clutter suppression algorithm based on fast converging sparse Bayesian learning for airborne radar[J]. Signal Processing, 2017, 130: 159-168.

[9] CHI Y, SCHARF L L, PEZESHKI A, et al. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Trans.on Signal Processing, 2011, 59 (5): 2182-2195.

[10] TEKE O, GURBUZ A C, ARIKAN O, et al. Perturbed orthogonal matching pursuit[J]. IEEE Trans.on Signal Processing, 2013, 61 (24): 6220-6231.

[11] YANG Z, XIE L, ZHANG C. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Trans.on Signal Processing, 2013, 61 (1): 38-43.

[12] WU X H, ZHU W P, YAN J. Direction of arrival estimation for off-grid signals based on sparse Bayesian learning[J]. IEEE Sensors Journal, 2016, 16 (7): 2004-2016.

[13] WEN C, XIE X M, SHI G M. Off-grid DOA estimation under nonuniform noise via variantional sparse Bayesian learning[J]. Signal Processing, 2017, 137: 69-79.

[14] LIU Q, SO H C, GU Y T. Off-grid DOA estimation with nonconvex regularization via joint sparse representation[J]. Signal Processing, 2017, 140: 171-176.

[15] 王天云, 陆新飞, 丁丽, 等. 基于贝叶斯压缩感知的FD-MIMO雷达Off-Grid目标稀疏成像[J]. 电子学报, 2016, 44 (6): 1314-1321.

WANG T Y, LU X F, DING L, et al. Bayesian compressive sensing-based sparse imaging for off-grid target in frequency diverse MIMO radar[J]. Acta Electronica Sinica, 2016, 44 (6): 1314-1321.

[16] 陈栩彬,张雄伟,杨吉斌,等.如何解决基不匹配问题:从原子范数到无网格压缩感知[J].自动化学报,2016,42(3):335-346.

CHEN X B, ZHANG X W, YANG J B, et al. How to overcome basis mismatch: from atomic norm to gridless compressive sensing[J]. Acta Automatica Sinica, 2016, 42 (3): 335-346.

[17] BAI L, ROY S, RANGASWAMY M. Compressive radar clutter subspace estimation using dictionary learning[C]∥Proc.of the IEEE Radar Conference, 2013: 1-6.

[18] BAI G T, TAO R, ZHAO J, et al. Parameter-searched OMP method for eliminating basis mismatch in space-time spectrum estimation[J]. Signal Processing, 2017, 138: 11-15.

[19] WANG J, KWON S, SHIM B.Generalized orthogonal match-ing pursuit[J].IEEE Trans.on Signal Processing,2012,60(12):6202-6216.