基于卷积神经网络的水下目标特征提取方法
2018-06-07王念滨王红滨郎泽宇
王念滨, 何 鸣,2, 王红滨, 郎泽宇
(1. 哈尔滨工程大学计算机科学与技术学院, 黑龙江 哈尔滨 150001;2. 黑龙江科技大学计算机与信息工程学院, 黑龙江 哈尔滨 150022)
0 引 言
水下目标自动识别是目标识别技术研究的一个重要领域,也是水声信号处理领域的突出难题。为此,国内外的学者们从多方面进行了研究,并且提出了多种解决方法。目前,水下目标特征提取存在的问题,单一特征表示的片面性,因此,如何把时域信号和频域信号有效的融合,实现基于信号融合的特征提取方法成为本文需要解决的关键问题。针对这样的问题,本文利用低频分析与记录(low frequency analysis and recording, LoFAR)谱图实现了两种信号的有效融合,LoFAR谱图保留了信号在时间和频率两个维度的信息。目前的特征提取工作需要大量的人工参与,这些操作都过于依赖人的主观意识和经验积累[1-4]。选取的特征不同对分类效果的影响也很大,同时对数据预处理也影响到特征提取的好坏。本文的研究就是针对当前研究的不足,对基于卷积神经网络(convolution neural network, CNN)的水下目标特征提取方法进行了研究。在本文的研究中,主要采用了具有端到端处理能力的深层神经网络,利用其自学习的特点隐式地提取目标特征并寻找到分类边界,最终提高了特征提取的质量。
1 卷积神经网络
1.1 卷积神经网络算法
CNN通过对输入数据的逐层线性和非线性映射处理,这种网络结构能够有效且更加抽象的描述出具有复杂分布的图像信息,从而提取出深层次的图像特征。
利用上述理论,本文把CNN在处理图像方面的独特能力,应用在对LoFAR图的处理上,进而对目标信号进行深层特征分析,最后利用提取到的深层特征进行水下目标的分类。
CNN 在对LoFAR图进行分析时,其卷积滤波器在沿着频率轴方向扫描时是对局部时间上不同频率信号进行分析的,这样会保留LoFAR谱图的短时平稳态信息,而滤波器在沿着时间轴方向扫描整个LoFAR谱图时又保留了信号的时序特性,进而实现了对信号从时域和频域两方面综合。卷积神经网络中每一层都是由多个二维特征图罗列而成,每个特征图中一个像素代表一个神经元节点[5-6]。网络中把神经元节点分为卷积神经元和池化神经元。池化神经元组成二维池化特征图,其激活值对应特征图像素值,而池化特征图的组合又形成了池化层[7]。卷积神经元、卷积特征图和卷积层之间存在类似的关系。CNN以卷积层和池化层交替栈式结构连接而成,网络将二维图像数据作为输入。区别于传统模式识别手段,样本的数据处理、特征提取以及分类流程都隐式的嵌入到这种深度互联结构的卷积网络中。一般情况下,卷积层又被称为特征提取层,前一层的某一局部感受野以适当大小输入到卷积层对应的神经元上,将这一过程称为提取局部特征,也就是说局部特征之间的位置关系较上一层的输入是未发生位置变化的;又将池化层称为特征映射层或下采样层,将每个特征图映射为一个平面[8]。为了保持特征映射过程中特征的位移、旋转不变性,卷积层的激活函数通常采用激活值不易发散的Sigmoid函数。另外,因为每个特征映射层上的神经元采用权值共享的原则,从而极大的减少了网络参数的数量,又避免了因过多的自由参数带来的过拟合现象[9]。网络中每一个特征提取层(卷积层)后伴随着一个特征映射层(池化层),这种带有池化结构的网络,可以使得模型对原始数据具有很强的降噪和抗干扰能力。
池化层中某一区域内的多个神经元,只有激活值大的那个神经元才能起到强化权值的作用,这也符合了“最大值检出假说”[10]。这种神经元在不断强化自身的同时还控制了周围神经元的输出结果,也就是特征映射图中提取到的特征为每个局部区域的相同特征。
通过图1可以看出,CNN结构以原始图像作为网络输入,图1中使用了4层网络结构,每层各个特征图中的相邻神经元以卷积核大小为单位,逐层将局部信息向下层传递,而下层则对传递过来的信息进行卷积运算即特征提取,如边缘特征或方向特征。网络的训练过程则是不断修改卷积核中参数的过程。而同一个卷积核是被特征图所共享的,可以视卷积核为一个可滑动的滤波器,扫描整个特征图的过程记为对某一特征进行提取的过程[11]。而作为二次特征提取的池化层更像是模糊滤波器。可以理解为将众多杂糅在输入数据中的特征信息经过网络的过滤最终分散到了各个低分辨率特征图上。

图1 CNN结构Fig.1 CNN structure
1.2 CNN在特征提取方面的适用性分析
二维图像中特征信息往往具有很强的隐蔽性,因为观测目标位置的变化,观察角度的不同等都会导致观测目标产生形变、位移甚至扭曲。然而,用显式的方法将图像中具有位移、缩放和扭曲不变性的特征提取出来的难度又是巨大的,即使存在也不具有广泛的适用性。
针对这样的问题,CNN的特征检测机制则给出了很好的答案。CNN的每次卷积运算都是针对局部特征进行的提取,因而目标的位置变化或缩放变化都不会对特征提取过程产生影响,并且CNN这种隐式的提取过程使得模型具有广泛的适用性。大量训练数据中的不变性结构信息在网络的特征空间中逐层被提取出来,又因为其结构的特点能与逻辑回归分类器进行无缝的融合,实现了端到端的图像处理方法[12]。其可以直接将图像输入到网络,并获得分类信息。避免了特征提取和分类之间的数据重构,而其中的特征提取过程隐藏在了网络结构当中。
由于特征图之间的权值是局部相连且权值共享的,基于这一特点可以将一个网络置于多个机器中同时进行训练实现并行的效果。其在计算和训练速度上明显优于其他全连接神经网络。
CNN模型的设计灵感来自于仿生学,其结构特点更接近生物神经网,所以在处理一些自然界的原始信号,如图像信息或声音信息时具有独特的优越性[13]。
可以概括出,CNN较其他网络模型在特征提取方面有如下优势:
(1) 检测数据可以直接作为网络的输入数据,无需任何预处理过程;
(2) 端到端的数据处理过程,简化了数据重建的复杂度;
(3) 权值共享的策略,在减轻了训练负担的同时,为训练提供并行化的可能。
2 特征图多维加权算法
由于原始输入通过深层网络得到的深层特征数据都是以特征图的方式呈现出来,而三维特征最终又都会通过一维向量化即全连接的方式输入到全连接层进行分类处理,其中,全连接层和卷积层的主要区别是卷积层嵌入了有大量的空间信息,而全连接层则没有[14]。卷积层的空间结构可以用一个三维张量来表示,其表示形式为H×W×D,其中,H与W表示卷积层中的一个卷积特征图的纵向神经元数目和横向神经元数目,D则表示层中特征图的数目。这种三维张量可以理解为卷积层将二维输入数据分解成了多个H×W的局部区域,而D维个这样的局部区域组成的集合一同描述着一种视觉模式。全连接层将卷积层得到的出作为输入,但是会将三维的特征图进行向量化,得到的一维特征向量代表分类器的特征向量。在这一过程中,空间信息会丢失并且空间特征不能在SoftMax层得到恢复,进而影响到分类准确度,并且在网络不断反馈调节时间接影响特征提取的质量。
2.1 特征图加权算法构建
针对上面提出的问题,本节提出一个简单直接的方法,来弥补上面所提到的因全连接层的一维向量化所带来的空间信息丢失。在最后一个特征图层向量化之前,本小节将会强化特征图层的空间信息,使得这种空间信息可以输入到最后的全连接层中。强化的角度则会从通道(channel)和空间(spatial)两个维度来增强,最后聚合为一维向量输入到全连接层。
强化特征图层空间信息的方法首先假设不同的特征图之间的重要程度是不一样的,比如有的特征图中包含的信息会比较单一,而有的会因为某些特征信息的数据表示是非线性的,所以经过深层过滤后的特征图里仍然包含许多信息。同样,每个特征像素的重要程度也是有区分的。基于以上想法,本节将给予不同特征图和特征像素赋予权值,来强化空间结构信息,进而提取高质量的数据特征。
针对多维加权算法的步骤和流程,在具体的赋权过程中,假设已经得到在一次前向传播过程中的最终特征图层,对该特征图层进行多维加权流程如下:
步骤1局部池化
对最后一层卷积层的每个特征图使用局部池化操作,池化窗口大小为w×h,窗口滑动步长为S。经过池化后得到一个三维张量。
步骤2计算空间(spatial)权重因子
对池化后的特征图上的每个特征像素都指派一个权重αij,对应特征图上的第(i,j)个像素。
步骤3计算通道权重因子
对于池化后的每个特征图即通道k,都赋予一个权重βk。
步骤4加权计算
将步骤2和步骤3计算得到的空间权值和通道权值赋予到其对应的位置上,最后得到一个带权三维张量。
步骤5向量归一化
针对以上数据进行归一化处理,得到聚合后的多维加权特征向量。
经过以上5步处理好的向量称为“多维加权特征向量”。在以上流程中,将最后一层卷积层进行池化操作的目的是为了起到特征二次提取的作用。同时,本池化操作方法还可以有效地降低待处理数据的规模。
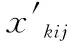
(1)
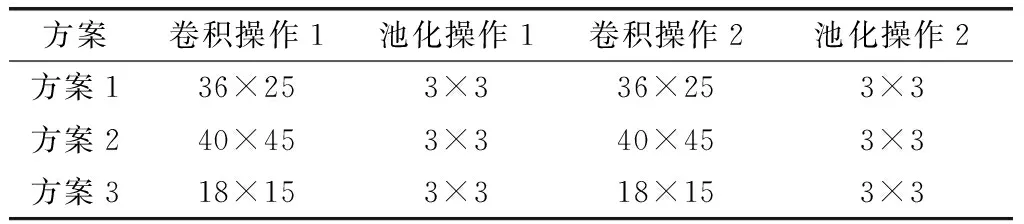
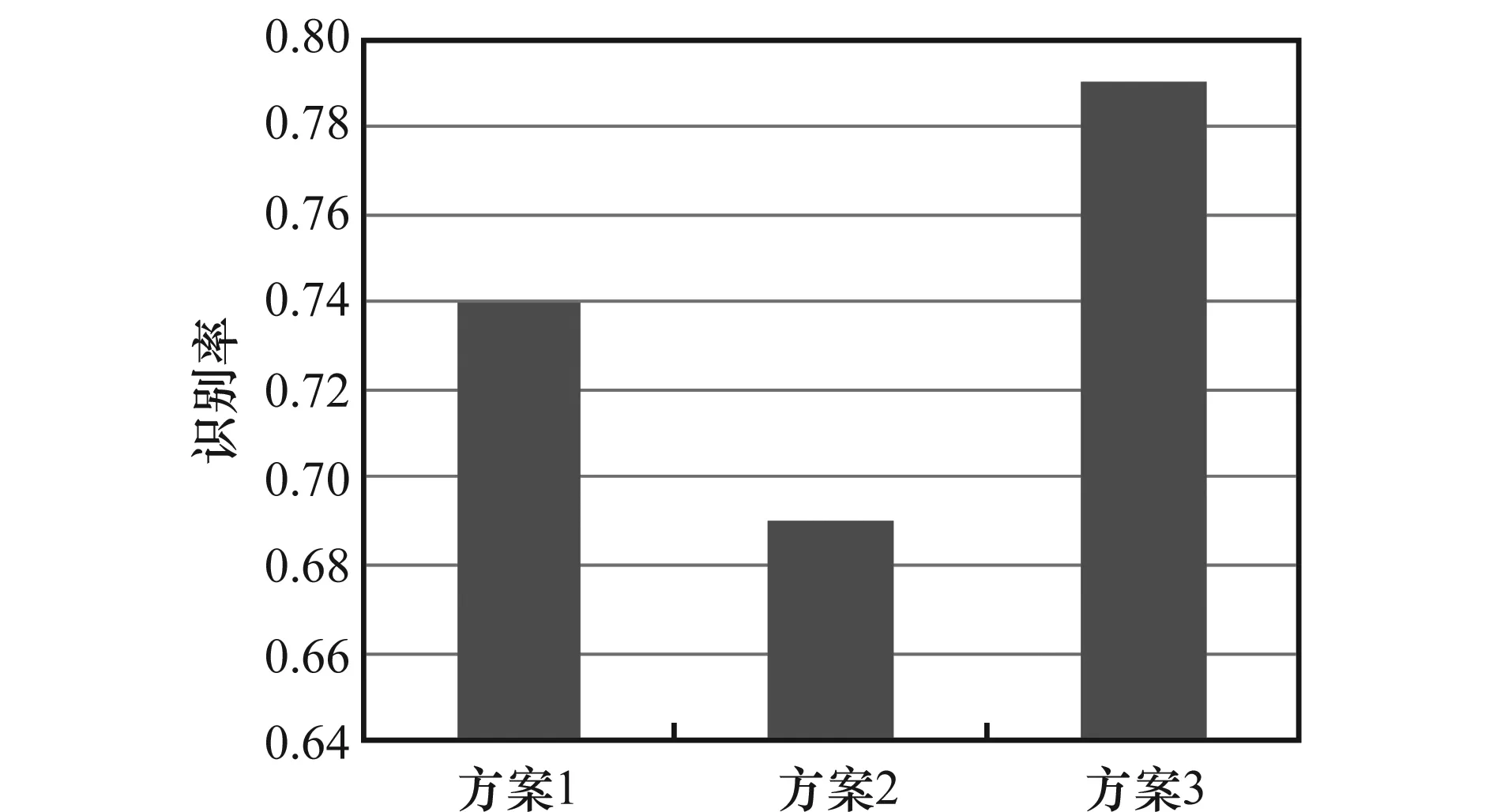
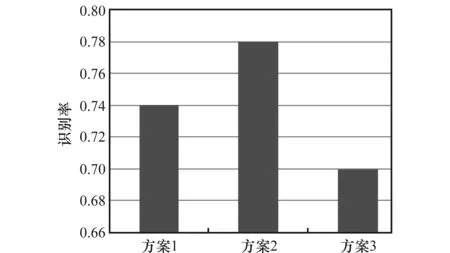
如图2所示的操作,卷积层的特征通过面向空间和面向通道两个维度进行了加权处理,从而强化了空间的结构信息。面向空间的权重因子集合A={aij|i 图2 特征加权过程Fig.2 Feature weighting procedure 最后再对χ′的每个特征图进行加和池化操作,将三维的带权特征张量聚合成一个一维的特征向量F={f1,f2,…,fk},其中fk计算为 (2) 通过以上的处理,已经将三维的带权特征张量聚合成一个一维的特征向量。下一步需要针对得到的特征向量F做归一化处理后再连入全连接层,进行聚合的主要目的就是为了减少全连阶层的输入规模,进而减少了需要训练的网络连接权值,从而避免过拟合现象发生。最后再将特征向量做归一处理,就是得到了最终的多维加权特征向量。 针对多维加权算法中的空间权重和通道权重,本文提出了两种无参数化的空间权重因子和通道权重因子的计算方法,其中,无参数化指的是不会对卷积网络带来额外的参数,而使其影响到网络的训练效率和可能发生的过拟合现象。 根据神经认知机对可塑性突触的形成的假设:如果在神经元y的近旁存在有比y更强的激活神经元y′,则从x至y的突触连接就不进行强化[15]。也就是说,这种突触连接的强化应符合“最大值检出假说”,即在某一小区域(称之为邻域)内存在的一神经元集合中,只有输出最大的神经元才发生输入突触的强化[16]。 从以上理论可以理解为,激活值越大的神经元对其附近的连接权值影响越大,其重要程度也就越大。那么定义Ck为三维特征张量χ中的第k个特征图,S∈RW×H为特征张量中所有特征图的累加,表示为 (3) 通过式(3)得到了初步的空间权值矩阵,其含义为将不同特征图的同一位置激活值xkij进行叠加,从而反映出平面空间上某一位置累计激活值的强度,即强度越大该位置也就越重要,该位置对应αij的值也就应该越大,之后对S进行归一化操作,得到最终的权值矩阵A,此处的归一化处理选取的是含有两个超参的归一化函数,表示为 (4) 式中,Sij表示S中第(i,j)个像素值,可调参数a与b的选取,可以根据网络训练情况而定。 对于面向通道上的权值向量的选取,本文提出了一种基于图像熵的加权算法。因为某些特征信息的数据表示是非线性和线性不可分的,所以经过深层过滤后的特征图里仍然包含许多信息。因此,对于每个特征图的重要程度可以用其中含有的信息量多少进行分析。 衡量信息多少的信息熵是从整个信息来源的统计特性上进行分析获得的,是从平均意义上来反映信源的总体特性[17]。对于某特定的信源,其信息熵只有一个。不同统计特性的信息来源,其信息熵也会有相应的变化。针对未知性较大的变量,其信息熵的个数也相对较多。 鉴于信息熵以上特性,本文引入图像熵的思想来衡量特征图中信息量的多少。虽然图像熵指的是整个图像中的平均信息量,但是一维的图像熵只能反映出图像中灰度分布的聚集情况,并不能表现出信息在空间的分布特征[18-19]。针对此问题,为了能与特征图相适应且同时反映出特征图中信息的空间分布特征,本文采用了二维图像熵的方法来解决该问题。在具体操作上,本文选择特征图的邻域激活均值作为激活值分布的空间特征量,与特征图内某一像素的激活值组成特征二元组。 图像熵中的灰度值是一个离散化的数值,而特征图中激活值是通过连续的激活函数得到的。所以在计算特征图的图像熵之前,本文采用等宽离散化的方法对特征图重新处理,实现连续数据的离散化,其中对每个像素点的激活值处理公式表示为 (5) 式中,x为某像素点的激活值;Xmax与Xmin为激活函数有效的下界和上界;m为离散后的区间长度。定义(I,J)为离散化后的特征二元组,其中I(0 (6) 至此本文给出的特征图熵值计算公式既反映出了特征图中所含信息量的多少,又强调了特征图中激活值与其邻域的信息分布情况。最后再对所有特征图的熵值进行归一化处理,即 (7) 本节以仿真实验的形式来分析卷积网络在水下目标特征提取工作上的有效性。将时域信号和频域信号进行融合的LoFAR谱作为卷积网络的输入数据,将输出的分类结果作为验证水下目标特征提取好坏的依据。 目前对水下目标的特征提取与识别工作都是利用辐射噪声的时序信号结构、功率谱特征或是时频谱图分析等手段展开的。所以在进行实验之前,先模拟出水下目标辐射噪声信号。为了保证模拟出的目标噪声信号具有真实环境下的结构,那么就必须研究它的声学线谱特性。现假定目标噪声由线谱和连续谱组成且符合平稳态随机过程,其中线谱通常分布在1 kHz以下的低频端。并将多组具有随机相位的正弦波作为目标信号的线谱分量,表示为 (8) 式中,K为线谱数量;Ak为第k条线谱的幅度;fk为线谱频率;φk为随机的相位。在模拟不同的信号时,fk控制在1 kHz以内。为了模拟真实环境下的噪声情况,在仿真的时序信号中混入幅值不同的高斯白噪声。 时频分析可以从LoFAR分析角度进行。虽然水下目标噪声信号具有非平稳性,但是在局部时间内还是具有平稳特性的。因此LoFAR谱图利用这一特点,将辐射噪声做短时傅里叶变换得到时变功率谱,并以时间顺序展开,得到关于时间和频率的二维图像。其具体处理流程如下: (1) 定义S(n)为原始辐射噪声信号的采样序列,将其分成K个连续部分,每个部分再设置L个采样点。其中K个连续部分之间允许有数据交叉重叠的部分,比如,交叉重叠度可以设置为50%,或者根据具体情况综合确定。 (2) 定义Mj(n)为第j段信号的采样样本,并对其做归一化和中心化处理,其目的是让辐射噪声信号的幅值在时间上分布均匀和达到去直流使样本的均值为零。 归一化处理 (9) 为了方便进行傅里叶变换的计算,通常将L的取值设置为2的整数次幂。 中心化处理 (10) (11) 将以上获得的各段数据的功率谱按时间顺序依次展开,即得到完整的LoFAR图。 虽然LoFAR谱图是二维的图像,横轴表示时间,纵轴表示频率,但反映的却是三维的信息。可以用灰度值的大小来表示在该时间和该频率下的能量大小。将LoFAR谱图作为水下目标特征提取的对象,是因为LoFAR谱图自身持有多维的信号信息,所携带的信息量丰富并且其二维的数据结构,正好满足具有特征抽取能力的卷积网络输入要求。 依据第3.1节所示方法获得实验样本集合,如表1所示。每组选取1 300个样本作为训练样本,余下的作为测试样本。训练样本约占总样本数的75%,而测试样本约占总样本数的25%。 表1 实验样本情况 其中传统CNN和特征加权CNN使用大致相同的网络结构,不同的是,加权CNN在内部增加一层加权层,最后一层为Softmax分类层。特征加权网络结构与参数如表2所示,其中网络的输入为224×224的LoFAR二维灰度图,第一层为8通道卷积层该层卷,感受野大小为5×5,且滑动步长为2;第二层池化层的输入大小是55×55,池化窗口为3×3,滑动步长为2。随后卷积池化层交替连接,再经过加权操作得到一维特征向量输入到全连接层。 表2 特征加权CNN参数 网络结构差异和网络参数的不同都有可能会对实验结果造成影响,以特征加权CNN结构为蓝本,分析滤波器大小和滤波器数量的不同对实验结果造成的影响以及在使用不同激活函数情况下的分类效果。 感受野的大小反映了对特征图处理的粒度,感受野越大,滤波器所提取的局部区域就越大,反映的特征就越粗化。极端情况下,感受野为整个特征图,那么提取的特征就是全局特征了。 现对滤波器按照表3所示的设计方案进行调整,再进行结果分析。 表3 感受野调整方案 上述感受野调整方案中,以方案1为基准,方案2则是向着感受野窗口增大的方向进行调整,也就是说粗化了特征提取的粒度;而方案3则是将感受野窗口减小,是向着更小的局部区域进行特征提取。从实验结果上可以看出,如图3所示局部感受野小的分类效果要优于局部感受野大的分类效果。当分析的窗口越小,则提取的特征越具体,越能反映出目标特有的类别信息。反之,提取的特征越没有表现力。 图3 感受野窗口对比结果Fig.3 Contrast results of receptive field window 对于卷积网络中的每一层来说,有多少个滤波器就对应着多少个特征图,每个特征图又对应着一个权值矩阵。每个滤波器又视为一个特征分析的分析角度,用所有滤波器的排列组合表征了上一层的数据特征信息。理论上越详尽越完备的滤波器组,对数据特征的分析能力就越强。但是过完备的滤波器组则会带来分析角度的冗余,并且会给网络带来更多的参数,进而影响到网络的训练效率。如果滤波器设置过少又不能完全覆盖输入信息的所有特征,反而使得分析能力弱化。本实验环节从向增加滤波器组数量和减少滤波器组数量两个方向进行对比实验。 具体滤波器组设计方案设计如表4所示。 表4 滤波器数量调整方案 实验结果如图4所示,增加滤波器数量确实可以使得识别率有所提升,这与之前的理论分析结果相一致。即更完备的滤波器组对特征表现力更强,相反相对单薄的滤波器组则对特征的表达能力不够。 图4 感受野数量对比结果Fig.4 Contrast results of receptive field quantity 网络节点中的激活函数主要起到对数据进行非线性变换的作用。这种非线性的操作可以让数据在空间中进行折叠、扭曲等形变,从而方便了寻找不同特征之间的划分边界。作为激活函数在具备非线性性质的同时,还应该具有平滑性、单调性和连续性。 同一个神经网络中是可以允许使用多种不同类型的激活函数的。基于常用使用策略,本实验环节采用单一激活函数策略。而常用的激活函数有Sigmoid、tanh和修正线性单元(rectified linear unit, ReLU)函数。 对于不同的应用背景,不同的激活函数带来的效果上的差别可能会很大。 Sigmoid函数作为最常用且普适的激活函数,将输入数据映射到0到1之间,利用该激活函数的网络可以使得网络具有较好的稀疏性。 tanh函数为双曲正切函数,该函数将节点输出值映射到了-1至1区间内。和Sigmoid相比,其健壮性更强,但是梯度消失的速度很快。对训练效率和网络收敛速度影响很大。 ReLU函数,其简单直接将小于0的激活值设置为0。这样可以保证能够抽象出更稀疏更离散的特征,这一特点与生物神经元很相似。而单一的稀疏性会使得输出数据的分布方差过大,即熵值过小。而离散性则表示的是神经元节点对刺激是很敏感的,即熵值较大。ReLU正是从两方面考虑,进而带来良好的性能。 几种激活函数对比图如图5所示,根据分析比较,在对LoFAR谱做特征提取时,Sigmoid激活函数的效果要优于其他两种。 图5 激活函数对比图Fig.5 Activation function contrast chart 本文主要在卷积神经网络进行了分析的基础之上,进一步分析了卷积网络在全连接操作时,会丢失特征图层的空间信息。为了弥补这一损失,本文提出了多维特征加权算法来强化待全连接的特征图。其中从空间和通道两个维度进行加权,而加权的策略则是根据最大检出假说和二维图像熵理论,即将空间中相同位置激活值的均值作为该空间位置的权重,将通道上每个特征图的图像熵值作为该通道的权重。并且该加权过程不会引入额外参数给网络训练带来负担。 由于时间和条件所限,本课题的实验中使用到的仿真数据,在后续的研究中应对真实的水下信号进行研究。 参考文献: [1] 杨西林,王炳和.水下运动目标谱特征提取与增强技术综述[J]. 水声及物理声学, 2007, 26(4): 69-72. YANG X L, WANG B H. Review of techniques for underwater moving target spectrum feature extraction and enhancement[J].Underwater & Physical Acoustics, 2007,26(4):69-72. [2] 张海龙,冶鑫晨,赵青,等.天文数据索引技术综述[J].中国科学:物理学·力学·天文学,2017,47(5): 059505. ZHANG H L, YE X C, ZHAO Q, et al. Astronomical data indexing technologies review[J]. Scientia Sinica(Physica,Mechanica & Astronomica) , 2017,47(5): 059505. [3] 宋振宇, 丁勇鹏, 赵秀丽, 等. 基于LOFAR谱图的水下目标识别方法[J]. 海军航空工程学院学报, 2011, 26(3): 283-286. SONG Z Y,DING Y P,ZHAO X L, et al. Target recognition method of LOFAR spectrum based on the underwater[J]. Journal of Naval Aeronautical Engineering Institute, 2011, 26(3): 283-286. [4] LIU J, HE Y, LIU Z, et al. Underwater target recognition based on line spectrum and support vector machine[C]∥Proc.of the International Conference on Mechatronics, Control and Electronic Engineering, 2014. [5] LECUN Y, BENGIO Y. Convolutional networks for images, speech, and time-series[C]∥Proc.of the Handbook of Brain Theory and Neural Networks, 1995: 255-258. [6] COHEN N, SHARIR O, SHASHUA A. On the expressive power of deep learning: a tensor analysis[C]∥Proc.of the Conference on Learning Theory, 2016. [7] SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al.Dropout: a simple way to prevent neural networks from overfitting [J]. Journal of Machine Learning Research, 2014, 15(1): 1929-1958. [8] JIA Y, SHELHAMER E, DONAHUE J, et al. Caffe: convolutional architecture for fast feature embedding[C]∥Proc.of the ACM International Conference on Multimedia, 2014:675-678. [9] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]∥Proc.of the International Conference on Neural Information Processing Systems, 2012:1097-1105. [10] HUANG Y M, XIA M Y, HUANG S. Evolutionary process unveiled by the maximum genetic diversity hypothesis[J].Hereditas,2013, 35(5): 599-606. [11] MASCI J, MEIER U, CIREAN D, et al. Stacked convolutional auto-encoders for hierarchical feature extraction[C]∥Proc.of the International Conference on Artificial Neural Networks, 2011:52-59. [12] VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11(12): 3371-3408. [13] CUI Z, CAO Z, YANG J, et al. A hierarchical propelled fusion strategy for SAR automatic target recognition[J]. Eurasip Journal on Wireless Communications & Networking,2013,2013(1):39. [14] ZHONG Z, LI J, CUI W, et al. Fully convolutional networks for building and road extraction: preliminary results[C]∥Proc.of the Geoscience and Remote Sensing Symposium, 2016:1591-1594. [15] OLSHAUSEN B A, FIELD D J. How close are we to understanding V1?[J].Neural Computation,2005,17(8):1665-1699. [16] 陈燕. 神经元的突触可塑性与学习和记忆[J]. 生物化学与生物物理进展, 2008, 35(6): 610-619. CHEN Y. Synaptic plasticity and learning and memory[J].Progress in Biochemistry and Biophysics,2008,35(6):610-619. [17] 李金才, 马自辉, 彭宇行, 等. 基于图像熵的各向异性扩散相干斑噪声抑制[J]. 物理学报, 2013, 62(9): 574-583. LI J C,MA Z H,PENG Y X,et al. Speckle reduction by image entropy anisotropic diffusion[J].Acta Physica Sinica,2013,62(9):574-583. [18] KIM S E, JEON J J, EOM I K. Image contrast enhancement using entropy scaling in wavelet domain[J]. Signal Processing, 2016, 127: 1-11. [19] WANG X, CHEN C. Ship detection for complex background SAR images based on a multiscale variance weighted image entropy method[J]. IEEE Geoscience & Remote Sensing Letters, 2017, 14(2): 184-191.
2.2 特征权值的计算方法分析

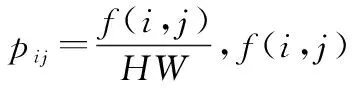
3 CNN的水下目标特征提取
3.1 仿真信号的获取
3.2 LoFAR谱的获取

3.3 数据集及网络结构


3.4 结果及分析


4 结 论
