基于复近似信息传递的多通道SAR成像方法
2018-06-07吴辰阳魏中浩张冰尘卢晓军
吴辰阳, 魏中浩, 张冰尘, 卢晓军
(1. 中国科学院电子学研究所空间信息处理与应用系统技术重点实验室, 北京 100190;2. 中国科学院大学, 北京 100190; 3. 中国国际工程咨询公司, 北京 100048)
0 引 言
随着合成孔径雷达(synthetic aperture radar, SAR)技术的不断发展,微波遥感领域在工程应用中对高分辨率和宽测绘带这两个重要指标的要求也变得越来越高。偏置相位中心天线(displaced phase center antenna, DPCA)技术[1]作为一种实现高分辨率、宽测绘带宽的有效技术手段,被广泛应用于高性能SAR系统研制中。为了实现最佳的成像效果,DPCA雷达成像系统需要满足方位向均匀采样条件,即系统脉冲重复频率(pulse repeat frequency, PRF)的选择需要使得一个脉冲收发时间内运载平台移动的距离恰好等于天线长度的一半[2],否则会导致方位向等效相位中心的周期性非均匀分布,进而使用经典的SAR成像算法会产生严重的方位模糊,限制了经典算法在多通道SAR处理中的应用。
针对多通道SAR方位向非均匀采样数据的处理问题,国内外学者也开展了相关的工作。Younis等人在文献[3]中提出基于相位补偿算法的多通道SAR处理方法,该方法通过对比多通道SAR信号与单通道均匀采样信号相位之间的关系得到关于多普勒频率的相位差,进而对多通道信号进行相位补偿使其等效于单通道均匀采样情况下的相位进行处理,但是该方法在系统的PRF与理想PRF偏离较大时,会对成像系统方位向分辨率造成较大影响;Krieger等人在文献[4]中提出基于多普勒频谱重建的多通道SAR处理方法,该方法将多通道SAR系统的信号采集过程近似地看成单通道SAR回波数据经过线性滤波器系统处理后的结果,当方位向回波数据满足奈奎斯特采样定理时,多通道多普勒频谱可以通过重建滤波器组实现无模糊重建,但是在回波数据存在加性噪声干扰情况下,方位向非均匀采样会使重建图像受到严重杂波电平干扰,进而对雷达图像解译造成不良影响;Lin等人在文献[5]中提出基于压缩感知的DPCA成像方法,该方法通过利用雷达回波数据和场景后向散射系数之间的时域关系从而建立精确的观测模型,利用稀疏成像算法实现无模糊图像的重建,但是矩阵-向量乘法运算所导致的巨大系统存储资源消耗严重限制了基于压缩感知的DPCA成像方法在实际大观测场景重建中的应用。
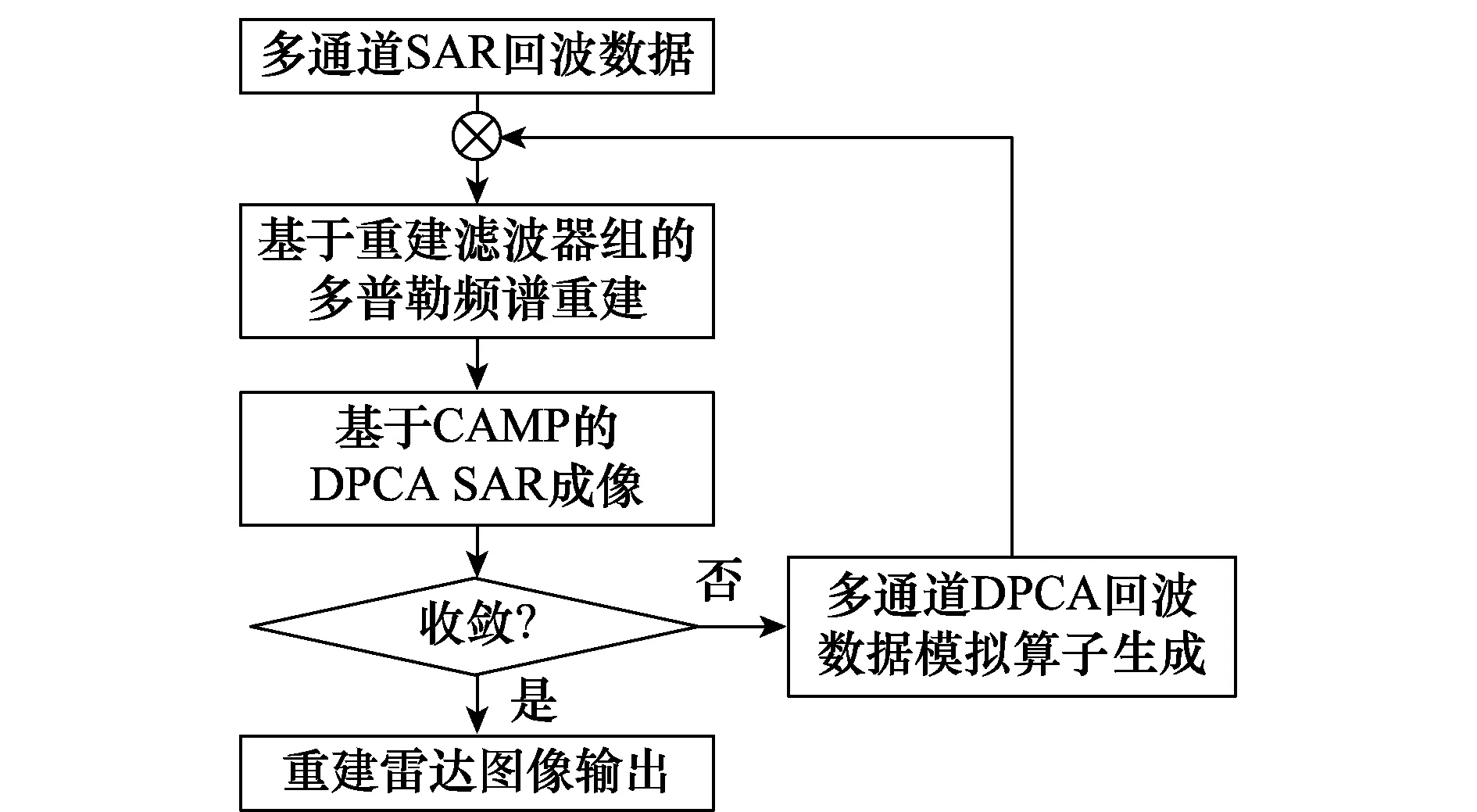
近年来,稀疏信号处理理论被广泛地应用于雷达成像领域[6-10],如三维SAR[11-13]、多输入多输出(multiple input multiple output, MIMO)雷达[14-16]、逆SAR[17-19]等,成为国内外学者的研究热点。根据稀疏微波成像理论,对SAR成像观测区域的重建过程可以通过求解Lq(0 基于CAMP的多通道非均匀采样DPCA成像方法原理流程如图1所示,主要包括基于重建滤波器组的多普勒频谱重建过程,基于CAMP的DPCA SAR成像过程,多通道DPCA回波数据模拟算子生成过程以及收敛判断过程,下面我们将对流程中的每一部分进行详细介绍。 图1 基于CAMP的多通道SAR成像方法原理图Fig.1 Schematic diagram of the multi-channel SAR imaging method based on CAMP 多通道SAR系统在方位向上采集的回波信号近似等于单通道SAR系统回波信号通过接收通道特性滤波器处理后得到[4,26],即 HC hi(f)≈Hm(f)·Hi(f) (1) 式中,HC hi(f),Hm(f)和Hi(f)分别代表第i个接收通道、单通道SAR、第i个接收通道特性滤波器在频域的冲击响应函数;Hi(f)包含恒定时间延迟Δti及相位偏移Δφi,因此接收通道特性滤波器在多普勒频域冲击响应函数可表示为 Hi(f)=exp[jΔφi]·exp[-j2πΔtif]= (2) 式中,Δxi代表第i个发射天线及接收天线相位中心的距离;λ代表载波波长;R0代表雷达和目标间的最近斜距;v代表平台移动速度。若每一个接收通道方位向采样频率为PRF时,n通道SAR系统方位向带宽则为n·PRF,因此可以通过接收通道特性滤波器Hi(f)构建特性矩阵H(f)来描述多通道SAR的系统特性,可表示为 H(f)= (3) 由广义采样定理[27]可知,采用1/n奈奎斯特采样率对某带限信号的n组独立表征进行采样,则可以对信号实现无模糊重建。因此,重建滤波器矩阵P(f)可以通过多通道SAR系统的特性矩阵H(f)求逆获得[4],即 P(f)=H-1(f)= (4) 式中,带通滤波器Pij(f)的频带宽度为[(j-1-n/2)PRF,(j-n/2)PRF],重建滤波器Pi(f)(i=1,2,…,n),Pi(f)由n个带通滤波器Pij(f)(j=1,2,…,n)组成。式(4)为求解重建滤波器P(f)的一般方法。 因此对于多通道非均匀采样系统,可通过上述方法推导相应重建滤波器组,并进行叠加,然后便可以通过单通道SAR成像经典算法或Lq正则化方法对多通道回波数据进行重建,进而得到观测场景的雷达图像。 Lq正则化稀疏重建算法在实现过程中,存在包含观测矩阵的矩阵-向量乘法运算,其计算复杂度和内存使用量均为平方阶,巨大系统存储资源消耗严重限制了在实际大观测场景重建中的应用。为了降低稀疏重建算法在多通道SAR成像中的计算复杂度和内存使用量,由多通道SAR成像原理以及逆成像回波仿真的思路,可以构建用来代替观测矩阵功能的回波数据处理算子[6,20-21],使其能够用于多通道SAR方位向非均匀采样数据的数据处理中。 我们使用经典距离多普勒算法作为单通道SAR系统的成像算法,多通道回波数据模拟算子主要由雷达图像重建与回波数据生成两个过程。图像重建过程主要由4个步骤组成,即距离脉冲压缩、多普勒频谱重建、距离徙动校正以及方位脉冲压缩,因此成像过程可以表示为 (5) 根据sinc插值基本原理,P(·)是可逆的,由逆成像回波仿真的思路,我们可以对式(5)表示的多通道雷达成像过程取逆,从而得到多通道回波数据模拟算子,即 (6) 式中,X为观测场景的后向散射系数矩阵;Hi为由Hi(f)的解析式计算获得的特性滤波器矩阵;上角标-1为相应算子的取逆,上角标*为矩阵的共轭。由此,我们便建立了用于处理多通道SAR系统方位向非均匀采样的回波数据模拟算子。 基于稀疏微波成像理论的Lq正则化SAR图像重建方法可以降低雷达图像中的旁瓣和杂波干扰,有效提升成像质量。Lq正则化问题可以表示为 (7) 式中,x∈CN×1表示观测场景的后向散射;y∈CM×1表示回波数据;Φ∈CM×N表示SAR系统的观测矩阵;λ表示正则化参数;‖·‖q表示向量的Lq范数,并且‖x‖q=(∑i|xi|q)1/q。CAMP算法作为求解Lq正则化问题的迭代算法,具有收敛速度快、重建精度高、抗噪性能好等优点,在获得观测场景稀疏估计的同时,还可以获取场景的非稀疏估计,保留了图像的背景统计特性。由于在CAMP算法重建过程中,存在包含观测矩阵的矩阵-向量乘法运算,其计算复杂度和内存使用量均为平方阶,巨大系统存储资源消耗严重限制了在实际大观测场景重建中的应用,因此,我们使用第1.3节中推导的多通道回波数据模拟算子代替观测矩阵的矩阵-向量乘法运算,因而可以有效降低系统复杂度和计算量,实现图像的高效快速重建。所以我们可以建立起基于多通道回波数据模拟算子的SAR成像模型: (8) 式中,‖·‖F表示Frobenius范数;vec(·)表示二维后向散射矩阵重新排列成一维向量。因此,基于CAMP算法的多通道DPCA SAR成像方法如表1所示。 表1 基于CAMP算法的多通道SAR成像过程 为了验证本文所提算法在多通道SAR系统方位向为非均匀采样时对重建图像方位模糊以及杂波电平的抑制能力,我们在仿真实验中采用一发三收的多通道SAR工作模式,在观测场景中设置一个面散射体作为观测目标,回波数据信噪比为20 dB,仿真参数如表2所示,等效的采样中心位置为周期性非均匀采样。我们分别使用距离多普勒成像算法、基于多普勒频谱重建的多通道成像算法和本文所提基于CAMP的多通道成像算法对方位向非均匀采样回波数据进行处理,不同算法非均匀采样重建实验结果如图2所示。 表2 仿真参数 图2 不同算法非均匀采样重建结果Fig.2 Reconstruction result of different algorithm with azimuth non-uniform sampling 2.2.1 模糊抑制能力分析 由仿真实验结果可知,由于一发三收SAR系统单通道回波数据方位向采样率为奈奎斯特采样率的三分之一,方位向回波信号的多普勒频谱会造成混叠,因此基于距离多普勒重建算法方位向非均匀采样重建图像中会产生大量方位模糊信号,模糊能量的电平约为-15 dB,对雷达图像成像结果影响明显,如图2(a)所示;基于多普勒频谱重建的多通道成像算法通过重建滤波器,实现对多通道方位向采样数据的多普勒频谱重建,由于回波信号沿方位向一阶近似所产生的相位误差未得到有效补偿,重建图像中存在部分方位模糊信号,模糊能量的电平约为-24 dB,如图2(b)所示;而基于CAMP的多通道成像算法作为一种稀疏重建算法,充分利用了观测场景的稀疏特性,进而在图像重建过程中有效了地抑制了由于非均匀采样带来的方位向模糊能量,并对观测目标有较高的重建精度,如图2(c)所示。 2.2.2 杂波抑制能力分析 为了定量评估不同SAR成像算法对重建图像背景杂波和噪声抑制方面的作用对重建结果中的杂波电平抑制能力,我们使用目标背景比(target to background ratio,TBR)[28]这一指标进行评估。在稀疏微波成像中,TBR值越大表示目标越突出,也就说明了背景中的杂波和噪声抑制效果越明显。为了比较多普勒频谱重建成像算法和基于CAMP的多通道成像算法杂波抑制能力,我们在回波数据信噪比在5 dB至15 dB的条件下,绘制了两种算法重建图像TBR和信噪比之间的变化曲线,如图3所示,当信噪比为5 dB时,基于CAMP的多通道成像算法重建图像的与多普勒频谱重建成像算法重建TBR之差约为12 dB,并且随着信噪比的增加,两种算法TBR差值有逐渐扩大的趋势。因此,基于CAMP的多通道成像算法能有效抑制重建图像中的杂波,降低背景杂波和噪声对目标识别的影响,实现更高质量的成像效果。 图3 不同算法重建结果目标背景比随信噪比变化情况Fig.3 Variation curves of TBR of reconstruction result with SNR via different algorithm 2.2.3 算法计算量分析 由表1可知,基于CAMP算法的多通道非均匀采样成像算法是通过sinc插值、相位相乘、归并排序以及快速傅里叶变换(fast Fourier transform,FFT)等基本算法操作实现。当以上算法操作的输出结果维度等于n时,其浮点运算量和内存使用量如表3所示[29-30]。通过将每种算法操作的浮点运算量及内存使用量相加可知本算法的浮点运算量与内存使用量分别为O(nlogn)和O(n)。而常规Lq正则化算法的浮点运算量及内存使用量均为O(n2),所以基于CAMP的多通道成像算法能更高效地实现成像且系统内存损耗更低。 表3 基本算法操作的浮点运算量和内存使用量 为了进一步验证本文所提算法性能,我们使用距离多普勒成像算法、多普勒频谱重建算法和本文所提基于CAMP的多通道成像算法对机载数据进行处理,实验使用的回波数据是由中国科学院电子学研究所C波段机载数据通过重插值模拟的“一发三收”SAR系统回波数据,观测场景为位于天津市的码头,其光学图像如图4所示。 图4 观测区域光学图像Fig.4 Optical image of the observation area 图5表示采用不同算法得到的重建图像,从中可以看出不同成像算法对雷达图像方位模糊及杂波电平的抑制效果。通过实验结果可知,距离多普勒算法重建图像如图5(a)所示,其中不仅存在杂波电平干扰,还存在方位模糊信号,在水面区域造成明显的虚假目标,影响图像判读;基于多普勒频谱重建的多通道成像算法重建图像如图5(b)所示,相比距离多普勒算法重建结果,通过对非均匀采样数据的多普勒频谱重建,该方法能有效去除方位模糊信号,但由于机载原始数据受到加性噪声干扰,在方位向非均匀采样程度较高时,会出现较严重的杂波电平;由于码头为典型的稀疏场景,基于CAMP算法的多通道成像算法可以实现对方位模糊信号和杂波电平的有效抑制,显著提升成像质量,重建图像如图5(c)所示。 为了定量评估不同算法在抑制图像背景杂波和噪声方面的效果,我们使用TBR作为评价指标[17],选取码头水面红框中的船只目标区域作为观测区域,得到3种方法重建图像目标区域TBR,如表4所示,相比于距离多普勒算法和多普勒频谱重建算法,本文所提基于CAMP的多通道成像算法能有效抑制背景杂波和噪声干扰,提升成像质量。 图5 不同算法非均匀采样重建图像Fig.5 Reconstructed image via different algorithm with azimuth non-uniform sampling 重建算法TBR/dB距离多普勒算法29.86多普勒频谱重建算法36.72本文所提算法55.37 本文针对多通道SAR系统方位向非均匀采样产生的方位模糊问题,提出了一种基于CAMP的多通道非均匀采样DPCA成像方法,通过将基于重建滤波器组的DPCA回波模拟算子与Lq正则化算法相结合,可以有效地解决多通道SAR因非均匀采样所产生的方位模糊以及杂波干扰问题,并有效降低计算复杂度和内存使用量,实现对观测区域的高精度重建,并通过仿真和实际数据实验验证了该方法的有效性。 参考文献: [1] CURRIE A, BROWN M A. Wide-swath SAR[J]. IEE Proceedings F Radar and Signal Processing, 1992, 139(2):122-135. [2] CALLAGHAN G D, LONGSTAFF I D. Wide-swath space-borne SAR using a quad-element array[J]. Radar, Sonar and Navigation, 1999, 146(3):159-165. [3] YOUNIS M, FISCHER C, WIESBECK W. Digital beamforming in SAR systems[J]. IEEE Trans.on Geoscience and Remote Sensing, 2003, 41(7):1735-1739. [4] KRIEGER G, GEBERT N, MOREIRA A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling[J]. Geoscience and Remote Sensing Letters IEEE, 2004, 1(4): 260-264. [5] LIN Y, ZHANG B, HONG W, et al. Displaced phase center antenna SAR imaging based on compressed sensing[C]∥Proc.of the IEEE IGARSS, 2011: 2692-2695. [6] ZHANG B C, WEN H, WU Y R. Sparse microwave imaging: principles and applications[J]. Science China Information Sciences, 2012, 55(8):1722-1754. [7] ZHANG B C, ZHANG Z, JIANG C L, et al. System design and first airborne experiment of sparse microwave imaging radar: initial results[J].Science China Information Sciences,2015,58(6):1-10. [8] 吴一戎,洪文,张冰尘,等.稀疏微波成像研究进展(科普类)[J].雷达学报,2014,3(4): 383-395. WU Y R, HONG W, ZHANG B C, et al. Current developments of sparse microwave imaging[J]. Journal of Radars, 2014, 3(4): 383-395. [9] QUAN X Y, ZHANG B C, LIU J G, et al. An efficient general algorithm for SAR imaging: complex approximate message passing combined with backprojection[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(4): 535-539. [10] WU C Y, WEI Z H, BI H, et al. InSAR imaging based on L1 regularization joint reconstruction via complex approximated message passing[J].Electronics Letters,2018,54(4): 237-239. [11] 毕辉, 蒋成龙, 王万影,等. 层析合成孔径雷达成像航迹分布优化方法[J]. 系统工程与电子技术, 2015, 37(8):1787-1792. BI H, JIANG C L, WANG W Y, et al. Track distribution optimization for tomographic synthetic aperture radar imaging[J]. Systems Engineering and Electronics,2015,37(8):1787-1792. [12] PENG X, TAN W, HONG W, et al. Airborne DLSLA 3-D SAR image reconstruction by combination of polar formatting and L1 regularization[J]. IEEE Trans.on Geoscience and Remote Sensing, 2016, 54(1): 213-226. [13] BAO Q, LIN Y, HONG W, et al. Holographic SAR tomography image reconstruction by combination of adaptive imaging and sparse bayesian inference[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(8): 1248-1252. [14] 李健,孙光才,左绍山,等.基于多普勒谱估计的多通道SAR盲重构方法[J].系统工程与电子技术,2017,39(10):2203-2208. LI J, SUN G C, ZUO S S, et al. Unambiguous reconstruction based on Doppler spectral estimation in multichannel SAR imaging[J]. Systems Engineering and Electronics, 2017, 39(10): 2203-2208. [15] HE X, LIU B, WANG D. Sparsity-driven frequency diverse MIMO radar imaging for moving targets[J]. International Journal of Information and Electronics Engineering,2013,3(4):409-413. [16] GU F F, ZHANG Q, CHI L, et al. A novel motion compensating method for MIMO-SAR imaging based on compressed sensing[J]. IEEE Sensors Journal, 2015, 15(4):2157-2165. [17] 冯俊杰,张弓.多测量向量块稀疏信号重构ISAR成像算法[J].系统工程与电子技术,2017,39(9):1959-1964. FENG J J, ZHANG G. Multiple measurement vectors block sparse signal recovery ISAR imaging algorithm[J]. Systems Engineering and Electronics, 2017, 39(9): 1959-1964. [18] XU G, XING M, ZHANG L, et al. Bayesian inverse synthetic aperture radar imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6):1150-1154. [19] CHEN Y J, ZHANG Q, LUO Y, et al. Measurement matrix optimization for ISAR sparse imaging based on genetic algorithm[J].IEEE Geoscience and Remote Sensing Letters,2016,13(12):1875-1879. [20] FANG J, XU Z, ZHANG B, et al. Fast compressed sensing SAR imaging based on approximated observation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 7(1):352-363. [21] JIANG C L, ZHANG B C, FANG J, et al. Efficient Lq regularisation algorithm with range-azimuth decoupled for SAR imaging[J]. Electronics Letters, 2014, 50(3):204-205. [22] QUAN X, ZHANG B, ZHU X X, et al. Unambiguous SAR imaging for Nonuniform DPC sampling: Lq regularization method using filter bank[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(11):1596-1600. [23] MALEKI A, ANITORI L, YANG Z, et al. Asymptotic analysis of complex LASSO via complex approximate message passing (CAMP)[J]. IEEE Trans.on Information Theory,2013,59(7):4290-4308. [24] ANITORI L, MALEKI A, OTTEN M, et al. Design and analysis of compressed sensing radar detectors[J]. IEEE Trans.on Signal Processing, 2013, 61(4):813-827. [25] BI H, ZHANG B, ZHU X X, et al. Lq-regularization-based SAR imaging and CFAR detection via complex approximated message passing[J]. IEEE Trans.on Geoscience and Remote Sensing, 2017, 1(9):1-15. [26] GEBERT N. Multi-channel azimuth processing for high-resolution wide-swath SAR imaging[D]. Dissertation: Karlsruhe Institute of Technology, 2009. [27] BROWN J. Multi-channel sampling of low-pass signals[J]. IEEE Trans.on Circuits and Systems, 1981, 28(2): 101-106. [28] CETIN M, KARL W C, CASTANON D A. Feature enhancement and ATR performance using nonquadratic optimization-based SAR imaging[J]. IEEE Trans.on Aerospace and Electronic Systems, 2003, 39(4):1375-1395. [29] CUMMING I G, WONG F H. Digital processing of synthetic aperture radar data: algorithm and implementation[M]. Norwood, MA: Artech House, 2005. [30] CORMEN T H,LEISERSON C E,RIVEST R L,et al.Introduction to algorithms[M].Cambridge,MA:MIT Press,2009.1 基于CAMP的多通道非均匀采样DPCA成像方法
1.1 基本原理
1.2 基于重建滤波器组的多普勒频谱重建
1.3 多通道DPCA回波数据模拟算子生成
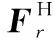
1.4 基于CAMP的多通道DPCA SAR成像算法

2 仿真实验与分析
2.1 仿真实验
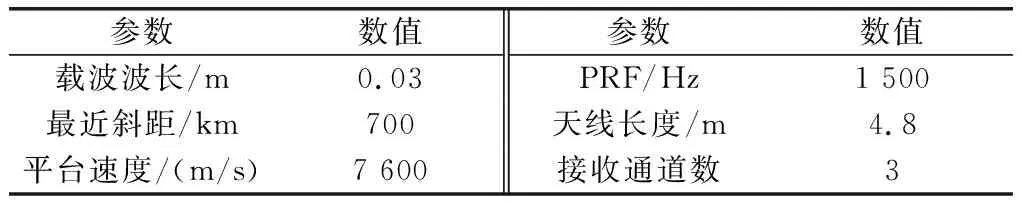
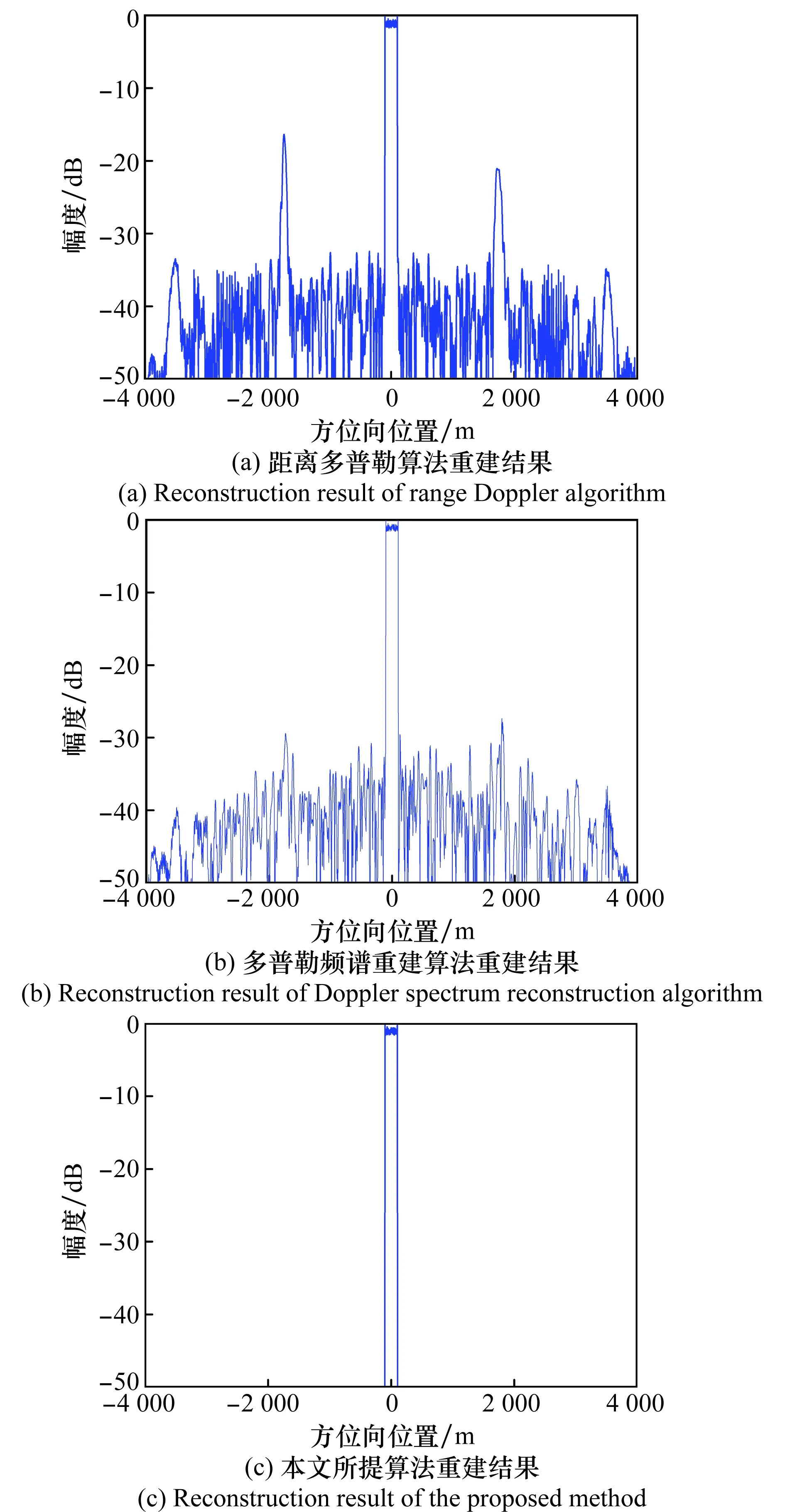
2.2 算法性能分析


3 实际数据实验处理



4 结 论
