基于SVM和Skyline查询的空地一体化攻击任务决策

李 波, 李曦彤, 高晓光, 崔四杰

(西北工业大学电子信息学院, 陕西 西安 710129)

0 引 言

随着未来空战目标性能的不断提高,空战模式的不断更新以及空地一体化综合作战理论的实现与发展,提高空战武器装备的毁伤效果和武器资源的利用效率日益关键。近年来,以美国为首的军事科技发达国家在空战导弹的技术研究方面不断取得突破,导弹网络化、多任务、多模制导等发展趋势已经成为必然[1-2],而实现多任务导弹在空地一体化作战中的攻击任务最优决策,是影响武器毁伤效果和利用率的关键,然而我国在相关方面可获取的研究成果甚少。

在未来的信息化战场中,一体化将成为对抗双方的博弈形式的重要特征,一体化作战的战场空间包括陆、海、空、网络等多维空间。而在空地一体化作战过程中,导弹可实现对空任务与对地任务两种任务类型的有效攻击,因此需要实时地综合整个战场信息,进行导弹攻击效能评估从而建立最优的任务决策系统,控制导弹有效攻击目标。传统的导弹任务决策系统主要基于目标威胁评估,空战态势评估,任务战场价值等方面进行目标分配,常用算法有遗传算法,蚁群算法,模拟退火,模糊逻辑算法等[3-4]。但这些方法在处理飞行环境的突发性变化问题时适应环境变化的能力较差,且多适用于对空或对地单种任务类型的目标分配,并不能很好地完成空地一体化综合作战中的双任务导弹任务决策。

本文在空地一体化综合作战的基础上,根据对导弹发射后攻击效能的实时评估,建立了适用于多任务导弹的攻击任务决策系统。当导弹不能有效命中原有目标但仍具有一定机动能力时,可以通过攻击任务决策系统进行任务切换,将攻击目标改变成当前其能够命中毁伤的最优目标。本文首先采用了基于支持向量机(support vector machine,SVM)理论的导弹空地任务类型决策算法,在样本数量有限的情况下有效减小了训练误差。又建立了基于Skyline查询算法的导弹目标任务决策方法,建立了级别不劣于关系模型,有效解决了导弹任务决策过程中处理高维数据时易出现的维数灾难问题和多属性决策中的完全补偿问题,最终确定导弹的最优攻击目标。

1 空地一体化综合作战系统

目前传统的空空导弹多采用典型的复合制导体制——“初制导+中制导+末制导”[5],为了有效提高武器资源利用率,空地一体化综合作战系统在传统空空导弹典型流程的基础上,引入了导弹在线评估系统和基于评估信息的导弹攻击任务决策系统,使导弹在不能命中原目标时具有动态切换对空或对地攻击任务类型和攻击目标的能力,从而使得作战形式更加灵活高效。导弹空地一体化综合作战流程如图1所示。

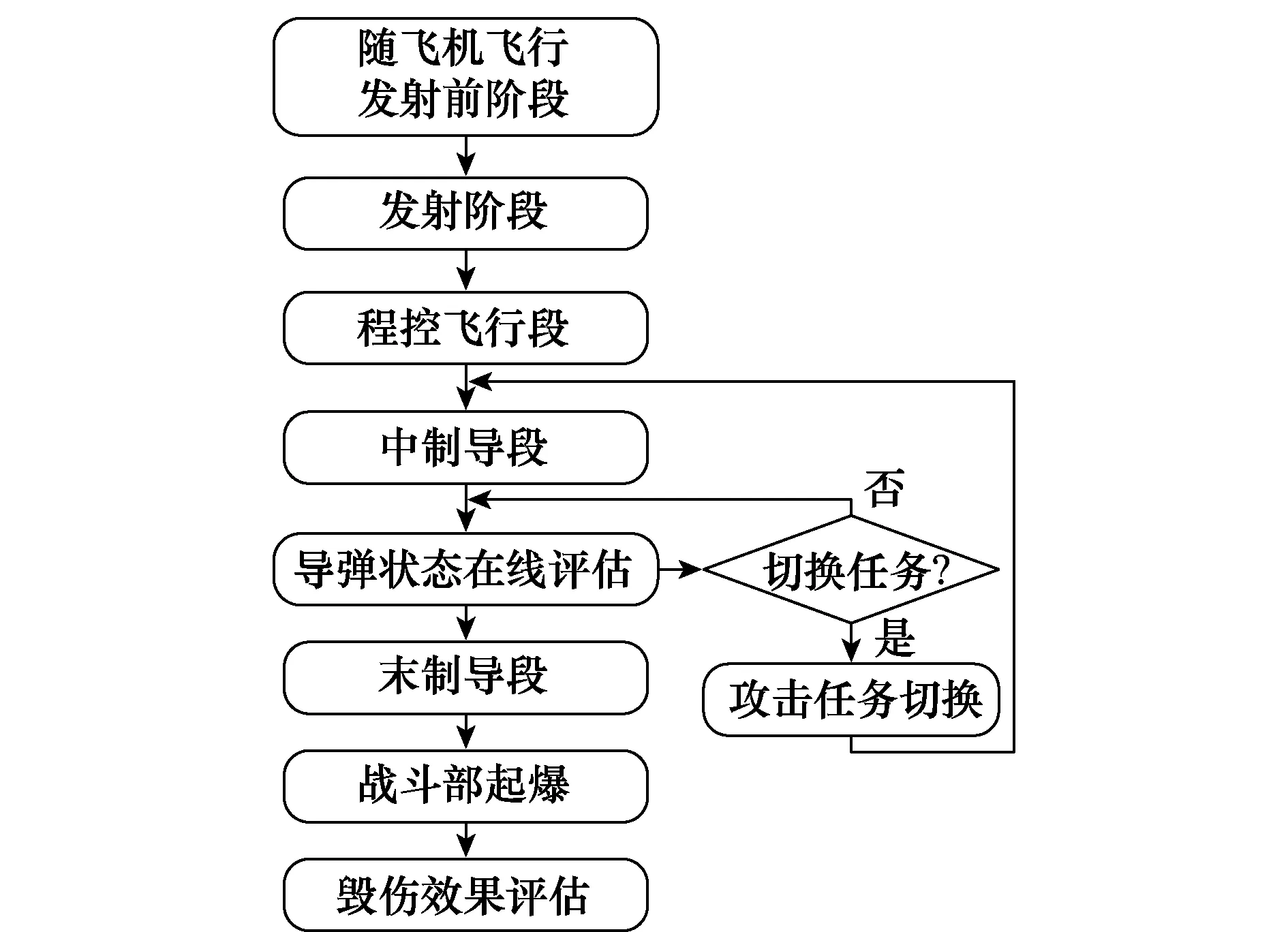
图1 导弹空地一体化综合系统流程图Fig.1 Flowchart of the air-ground integrated system

由图1可知导弹的空地一体化综合作战在导弹的中制导阶段,进行了对导弹和目标状态信息的实时在线评估,根据反馈的评估信息决策导弹是否进入任务切换阶段;在任务切换阶段,评估导弹性能和战场各目标的相对态势,决策导弹下一时刻所要攻击的最优目标,实现导弹的再次攻击,从而提高导弹的作战效能以赢得战机。

2 导弹攻击任务决策系统

在未来的空地一体化综合作战中,考虑到战场复杂的电磁环境,目标的隐身能力和机动逃逸能力都有可能导致导弹发射后最终不能有效命中原有目标,而载机在导弹导引头捕获目标之前都需要对导弹进行指令制导,即有些情况下,载机是在对不能命中目标的导弹进行制导,从而浪费了时间,并延误了战机。因此,本文建立的导弹攻击任务决策系统首先进行对导弹状态的在线评估,即判断导弹在当前飞行状态下能否有效命中原目标,根据输出的评估信息决定导弹是否进入攻击任务切换决策阶段,从而避免载机对导弹的无效指令制导时间,也增加了导弹再次攻击目标的机会。

2.1 导弹状态在线评估

面对瞬息万变的战场,为了对导弹的攻击任务做出最佳决策,需要首先对导弹与战场上各个目标进行实时的攻击效能评估。鉴于机载计算机的计算性能有限,且对导弹性能的在线评估计算需要一定时间,本文采取了间隔性的周期评估以满足实时性的要求,导弹状态在线评估系统的基本流程如图2所示。

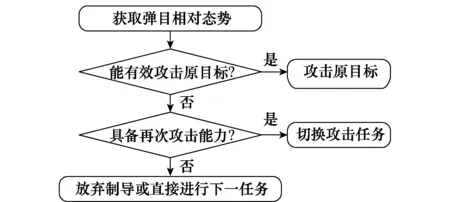
图2 导弹状态在线评估系统流程图Fig.2 Flowchart of the missile online assessment system

2.1.1 导弹攻击效果评估

导弹攻击效果在线评估的目的是实时地估计导弹发射后每刻的最终命中情况。本文采取导弹发射到进入末制导或者已放弃制导之间的时间段作为攻击效能在线评估的时间段。

为了满足战场上信息获取使用的实时性要求,首先以当前时刻的导弹、目标信息为初始态,进行一次快速的弹道模拟,预测出导弹最终能否命中目标。若评估信息显示导弹仍然能够有效地命中当前目标,则导弹继续攻击该目标。此时输出的评估信息为导引头对目标的截获概率P截获和导弹对目标的杀伤概率P杀伤[6-9]。

一旦评估信息显示中该导弹命中原目标失败或攻击原目标失败,此次评估结束,返回此时的累计评估时间和评估时刻作为评估结果并进入导弹当前性能评估阶段。

T_Fbegin=Tevalution(MissileBeginFailure)

(1)

T_Ftotal=n×T

(2)

式中,T_Fbegin为导弹开始命中失败的评估时刻;T_Ftotal为导弹命中失败的累积评估时间;T为评估周期;n为命中失败的累计评估周期数。

2.1.2 导弹当前性能评估

导弹当前性能值的在线评估,是判定导弹当前状态下是否具有再次攻击能力的关键指标[10]。

导弹在飞行状态下的性能与导弹已飞行时间t,导弹当前飞行速率v,导弹剩余燃料量等有关。选取导弹已飞行时间和导弹当前飞行速率作为导弹当前性能的评估指标参数,则导弹的当前性能值SM为

SM=SM(t,v)=a1Tt(t)+a2Tv(v)

(3)

式中,Tt(v),Tv(v)分别为导弹当前已飞行时间t、当前飞行速率v的函数;ai(i=1,2)是加权系数(ai>0且a1+a2=1)。由于相比于导弹当前飞行速度,导弹已飞行时间更能够体现导弹性能的损耗及当前性能,故宜取a1>a2。导弹已飞行时间t越大,导弹的当前性能值SM越小;导弹当前飞行速率v越大,SM越大。综合考虑导弹的推力作用时间tb、导弹的有效飞行时间ts以及导弹的最大飞行速率vmax,可得到Tt(v),Tv(v)的表达式分别为

(4)

(5)

式中,ξ(0<ξ<1)为权重系数。

选取S0作为判定导弹是否具有再次攻击能力的当前性能值的临界值,则SM≥S0时,导弹具有再次攻击能力;否则,导弹不具有再次攻击的能力,应当及时放弃对该导弹的制导进入下一阶段的作战。

2.1.3 弹目相对态势评估

当判定导弹不能命中原目标且仍具有再次攻击能力时,需要计算战场上各目标与导弹之间的相对态势关系,弹目之间的相对角度越小、相对速度越大、相对高度越小,则导弹攻击目标时所需的机动能力越小,对导弹命中目标越有利。依据构造的态势矩阵进行导弹攻击任务决策,选取导弹下一刻的最佳攻击目标。本文选取的导弹与目标之间关键相对态势[10]包括:

(1) 弹目相对角度指数

(6)

式中,q为导弹速度矢量与目标线之间的方位角。

(2) 弹目相对速度指数

(7)

式中,v为导弹速率;vt为目标速率;vmax为导弹最大飞行速率;min(vt)为当前参与决策目标中最小速率。

(3) 弹目相对距离指数

(8)

式中,Dmax为导弹当前状态下的最大攻击距离。

(4) 弹目相对高度指数

(9)

式中,H为导弹高度;Ht为目标高度;Hmax为导弹的最大飞行发行高度;max(Ht)为当前所有参与决策目标中最大高度。

2.2 导弹攻击任务切换决策

当评估信息显示导弹不能有效命中原目标并有能力进行攻击任务切换时,首先建立基于支持向量机原理的导弹空地任务类型切换决策算法,再根据在线态势评估矩阵,利用Skyline查询算法求解导弹攻击的非劣解目标集合,并在非劣解目标集合中建立级别不劣于关系最终解得导弹下一时刻所应攻击的最优目标,本文建立的决策方法即克服了传统攻击任务决策在战场决策中的延时问题,也保证了所求得的最优目标一定是非劣解目标,更加具有合理性。

2.2.1 导弹空地任务决策

SVM是从线性可分情况下的最优分类超平面发展出的一种常用的统计学习方法,在解决小样本,非线性和高维数问题中相比于神经网络等其他机器学习算法表现出许多特有优势[11-14]。

空地一体化作战系统中导弹在下一时刻进行对空任务还是对地任务与导弹当前任务类型状态(对空或对地)、导弹当前性能、导弹与战场各目标之间的态势有关。因此选取导弹当前任务类型{-1,1}{对空任务,对地任务}、导弹当前性能值、距离导弹最近的地面目标的弹目距离、距离导弹最近的空中目标的弹目距离作为训练样本的输入项。为避免输入变量差异较大,首先将训练样本数据中的输入量进行归一化。训练样本数据中的输出量,即每个样本相应的导弹空地任务类型可由专家指定或者经过实际作战演练获得。由于导弹的空地任务类型决策问题属于高维的非线性问题,且为了克服样本空间中可能存在的少数错误样本带来的误差,本文引入松弛项的“软间隔”非线性支持向量机(nonlinear support vector machines, NLSVM)[15],采用相对其他形式核函数具有更优性能的高斯核函数(radial basis function, RBF)替代高维特征空间中的点积[11-16]。利用“软间隔”NLSVM理论构建导弹空地任务切换决策问题的最优超平面的详细算法如表1所示。

表1 导弹空地任务切换决策算法

计算中拉格朗日乘子αi,αj的选择原则是选取最大违反KKT条件[11]的变量对αi,αj,参数当所有的αi(i=1,2,…,l)满足KKT条件时,循环终止,输出训练好的支持SVM相关参数。

2.2.2 导弹目标任务决策

在确定导弹下一时刻的空地任务类型后,就要根据态势评估矩阵求解导弹下一时刻的最优攻击目标,首先需要求解弹目态势各属性集P={P1,P2,…,Pn}所对应的权重向量w=(w1,w2,…,wn)T,求解流程如图3所示。由图3可知,当判定CR>0.1时,则需要对矩阵B中的元素作调整,由于判断矩阵B内绝大多数元素都能反映专家的决策意图,因此对判断矩阵元素调整的个数要尽可能少。本文所采用的权重向量计算方法在最大程度上保留了专家经验。

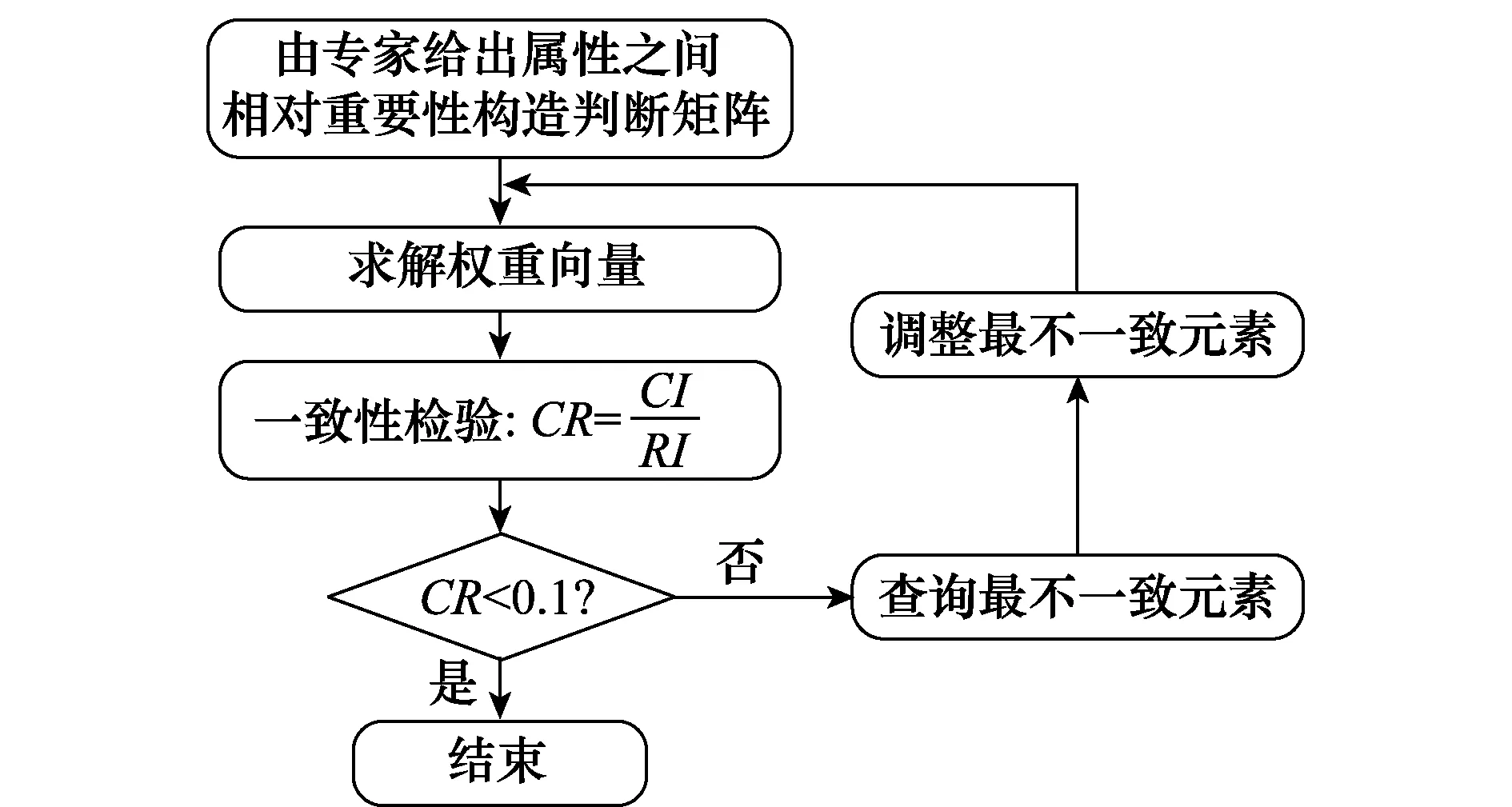
图3 权重向量求解流程Fig.3 Flowchart of updating the weight vector

Skyline查询的基本思想就是在寻找数据集Γ中所有不被其他点支配的Skyline点的集合[17]。Syline查询方法在处理高维数据时相有着良好的性质,可以克服维数灾难和重要信息丢失等现象[18]。本文就是利用Skyline查询的技术特点,首先在目标集合中选取非劣解目标集合,然后在非劣解目标集合中求解最优目标,以分配给将要进行任务切换的导弹。

经典的Skyline查询算法主要有:块嵌套循环算法(BNL)、分治算法(D&C)等,文献[19-20]在D&C算法的基础上,建立了Skyline-树的方法,读入数据时动态的对数据进行划分,只需与树中和该数据具有相同特性的部分结点进行比较,以达到减少比较次数的效果。本文在文献[20]的基础上,修改Skyline-树根节点的选取方法,防止根节点被之后读入的数据支配,从而进一步减小比较次数。

步骤1选取根节点

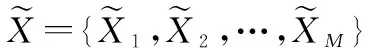
(10)

步骤2划分区域(子树)

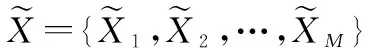
(11)

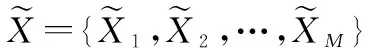
由于非劣解树不会含有特征串为00…0和1…11的子树。故所建立非劣解树共有2n-2个子树,它们的特征串范围为[00…01,11…10]。

步骤3与根节点进行支配关系检查

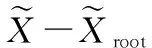
步骤4与对应子树中的目标进行支配关系检查

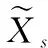
步骤5遍历树,删除伪非劣解目标

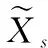
随后,记目标决策矩阵为A=[aij]m×n,(aij∈[0,1]),aij表示目标Xi对应于目标属性指标Pj的指标值,则目标Xi的指标值向量为ai=(ai1,ai2,…,ain)。传统的多属性决策分析方法一般是将目标进行完全排序[21],然后选择最优目标,为了克服属性间的完全补偿关系导致的决策结果不够合理,本文建立级别不劣于关系[22],引入一致指数和不一致指数,分别反映对“目标Xi不劣于目标Xj”的支持和反对程度。不一致指数可以理解为否决,意味着,如果目标Xi在属性Pk的表现太差无法接受,那么该目标在其他属性上的较好表现也无济于事。下面给出由非劣解目标集合X求解最优目标的具体算法步骤:

步骤1构造加权规范化矩阵V=[vij]m×n;

步骤2确定一致集C(Xi,Xj)和不一致集D(Xi,Xj);

步骤3计算一致指数c(Xi,Xj)和不一致指数d(Xi,Xj);

步骤4确定优势矩阵F={f(a,b)}和劣势矩阵G={g(a,b)};

步骤5确定综合优势判定矩阵E={e(a,b)};

步骤6确定目标之间的优劣关系。

按上述步骤解得导弹非劣解目标集合X中不劣于其他目标的目标集合N,显然,在N内部目标之间仅存在不可比关系。若N仅含有一个目标,则该目标即为导弹下一时刻的最优攻击目标;若N中元素个数大于1,则对N中的目标计算f(Xi)=ai×w即可确定最优目标。

3 仿真与分析

3.1 仿真实验

实验条件:假设导弹发射10 s后,该导弹所攻击的目标进行最大过载的“S”形机动逃逸以规避导弹,使得该导弹无法命中原定目标。导弹及其初始目标的初始化参数如表2所示。弹目态势各属性之间比重如表3所示。假设此时战场与该导弹位置最近的空中目标和地面目标的位置和速度信息见表4所示。且假设导弹至多可进行一次任务切换。

表2 导弹及其初始目标的初始化参数

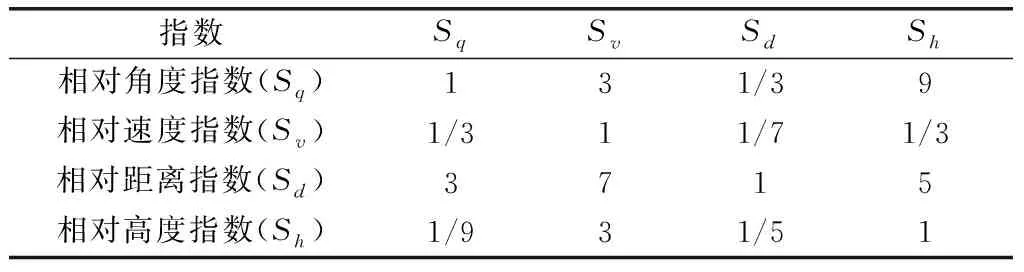
表3 弹目态势各属性之间比重

表4 导弹将切换任务时距导弹最近的空/地目标信息

其他相关参数如表5所示。

表5 其他相关参数

实验1导弹状态在线评估。

由表2可知导弹发射后飞行10 s时,导弹位置矢量为(8 728.2,5 000,2 244.6)m,速度矢量为(1 364.7,0,539.7)m/s,则导弹当前飞行速率为1 467.5m/s,根据式(3)～式(5)计算出导弹当前状态下的性能值为SM=0.809 0>S0,故导弹具有再次攻击能力。

实验2导弹空地任务切换决策模型的支持向量机训练与测试。

首先对SVM的训练样本和测试样本中的数据进行预处理:设距导弹当前位置最近的地面目标的距离的取值范围为minDG∈(0,50 km],距导弹当前位置最近的空中目标的距离的取值范围为minDA∈(0,50 km],以此对minDG和minDA进行归一化。然后,以表5中C,σ的取值进行支持向量机训练,并用训练好的支持向量机对测试样本进行测试。选取30个测试样本中部分测试结果如表6所示。

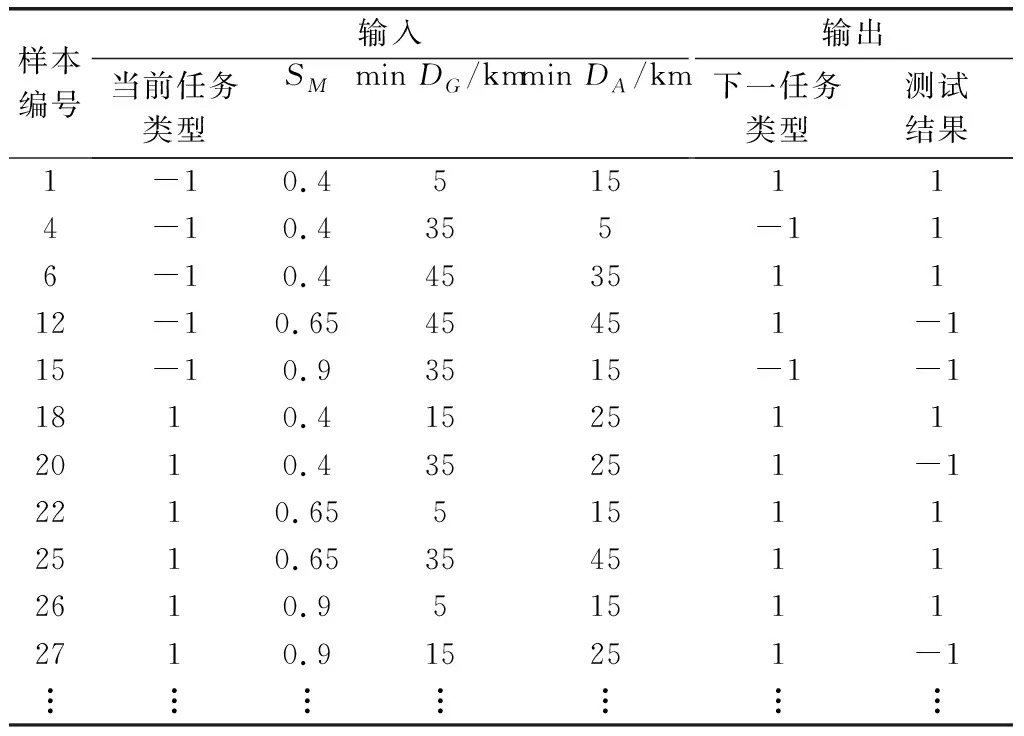
表6 SVM部分测试样本

实验3导弹空地一体化作战攻击任务决策。

由于导弹发射后不能有效命中初始攻击目标,因此首先对导弹下一阶段攻击任务类型进行决策。由表4可知导弹发射后飞行10 s时,距导弹当前位置最近的地面目标的距离为minDG=24 402 m,距导弹当前位置最近的空中目标的距离为minDA=103 015 m。进行归一化后值为0.488 0、0.206 3,将{-1,0.809 0,0.488 0,0.206 3}输入到训练好的支持向量机,输出为-1。故导弹在下一时刻应当进行对空任务。

根据表3所提供的判断矩阵计算出权重向量:

w=(0.194 6,0.066 4,0.584 9,0.154 1)T

(12)

随后对导弹切换攻击的目标进行决策选择。设导弹当前状态下的最大攻击距离为50 km。根据导弹此时任务切换决策目标集合计算出各目标的弹目态势集合。选取部分结果如表7所示。

利用Skyline计算原理求解非劣解目标编号集合X为{1,5,12,13,15,17,31,33,38,41,42,46,47}。由该非劣解目标集合和导弹目标任务切换决策模型的权重向量,求解导弹下一时刻的最优攻击目标。决策结果为:导弹下一时刻的最有攻击目标为目标1。在时间为14.70 s时导弹导引头截获目标,在时间为18.80 s时,导弹命中目标。整个导弹空地一体化综合作战中的弹道曲线如图4所示。

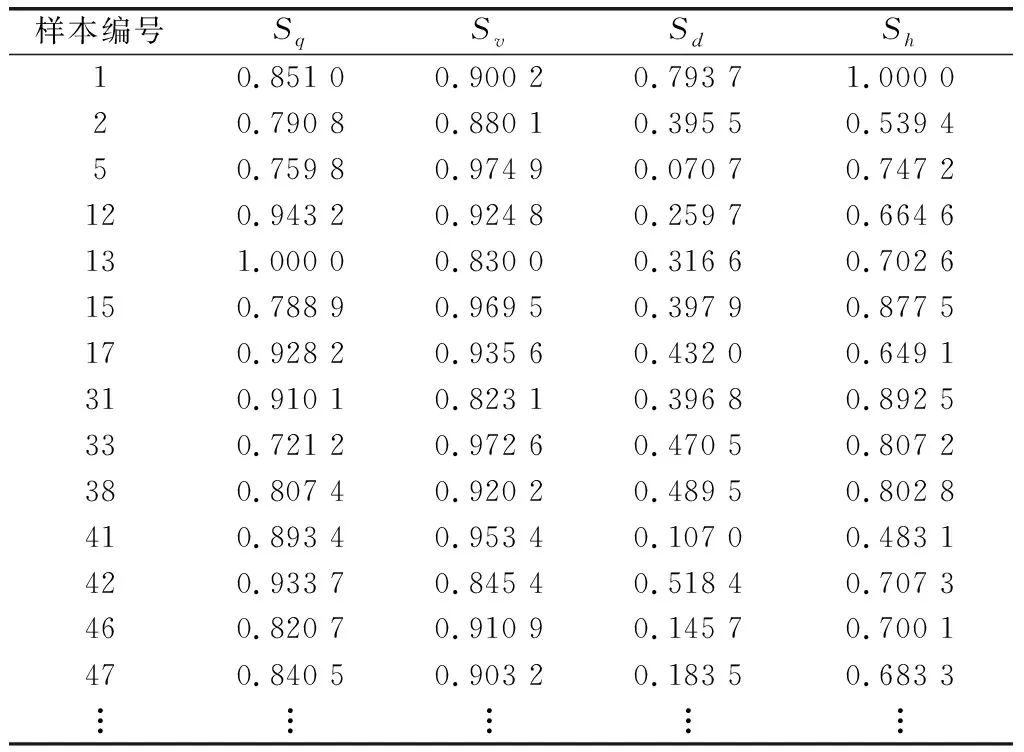
表7 部分弹目态势集合

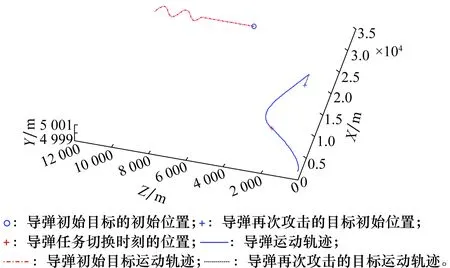
图4 导弹空地一体化综合作战弹道曲线Fig.4 Trajectory curve of the air-ground integrated missile

3.2 实验结果分析

由表6可知,30个测试样本中仅有4个样本的预测结果错误,故测试样本的预测正确率为86.67%,且从统计学理论上讲支持向量机的推广能力十分优秀。由此可验证本文的导弹空地任务决策算法能够有效准确地对导弹下一时刻应该进行对空任务或对地任务这一问题做出决策。

导弹导引头截获概率和导弹杀伤概率在线评估结果曲线如图5所示。

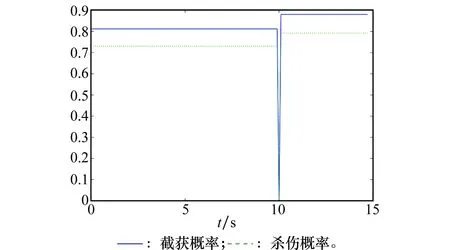
图5 导引头截获概率和导弹杀伤概率在线评估结果曲线Fig.5 Curve of the online assessment results of the intercept probability and kill probability

由图5可知,导弹发射后,导弹在线评估系统开始进行周期性的攻击效果评估,前10 s内由于目标未做机动,故导弹可有效杀伤目标且评估结果趋于稳定。

导弹发射后飞行10 s时,目标进行逃逸机动,导弹实际上已不能有效命中杀伤原目标,此时导弹的在线评估结果为导引头截获概率和导弹杀伤概率皆为零,与实际情况一致,由此可验证本文的导弹攻击效果在线评估方案有效地解决了导弹发射后对目标攻击效果的实时预测问题,为导弹下一阶段的攻击任务决策提供了基础。

在导弹的攻击效果在线评估结果为不能有效命中原目标时,对导弹当前性能进行评估,判断导弹是否具有再次攻击能力,本实验依据导弹当前状态判定该导弹具有再次攻击能力,导弹最终命中切换后的目标的实验结果也验证了该判断的正确性。

导弹过载曲线如图6所示,由图6可看出在导弹发射后10 s时,导弹过载急剧增大,这是由于导弹在此时进行目标切换,导弹需要较大的过载进行方向的调整。

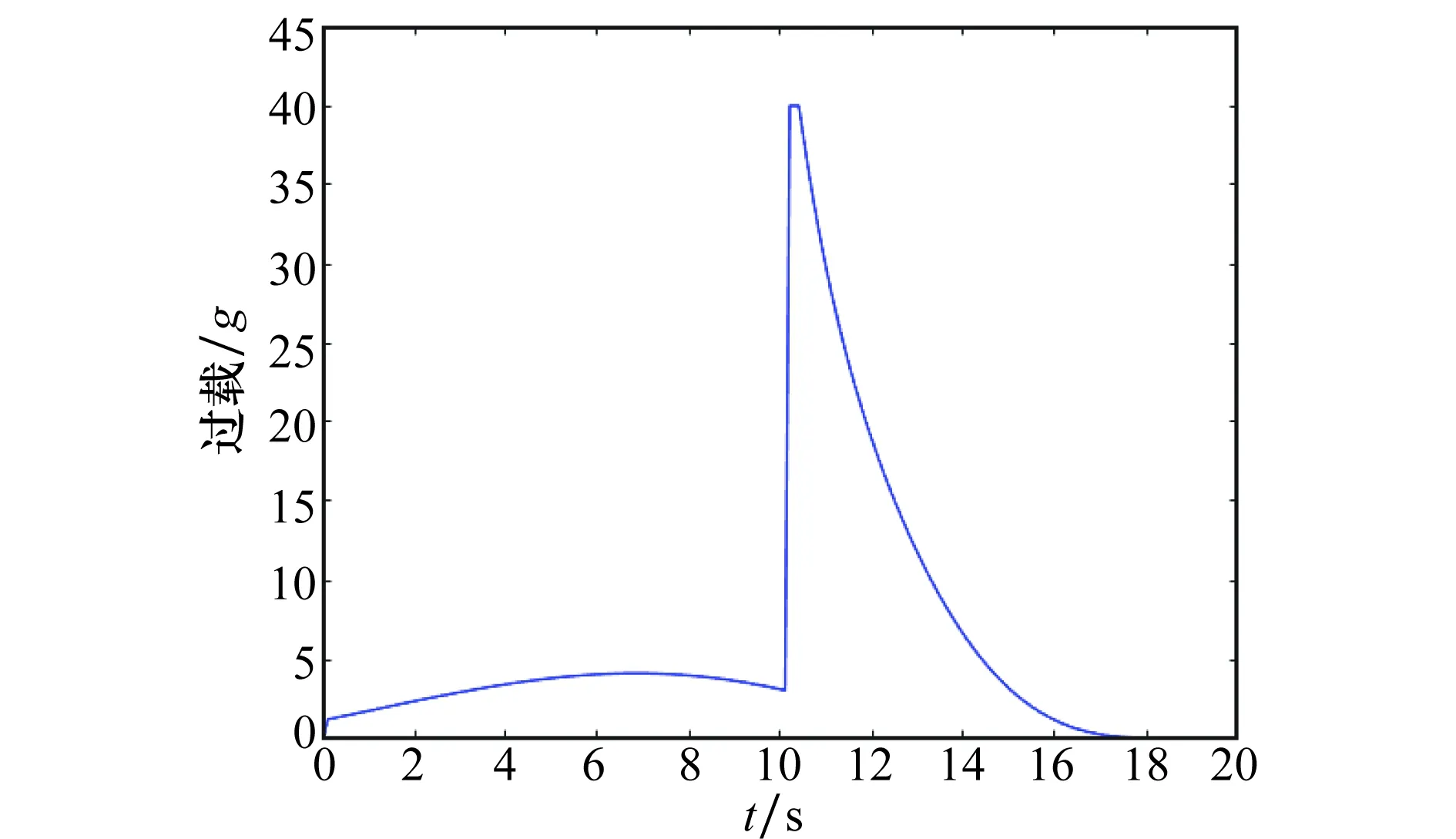
图6 导弹空地一体化综合作战导弹过载曲线Fig.6 Curve of the overload of the air-ground integrated missile

4 结 论

本文设计的导弹攻击任务决策系统有效地解决了在空地一体化综合作战中多任务导弹的最优攻击任务决策问题。本文将攻击任务决策分为导弹状态评估和攻击任务切换决策两个阶段,任务切换决策阶段分为空地任务类型切换决策和目标任务切换决策两部分完成。首先利用“软间隔”NLSVM理论在小样本的情况下低错误率的对下一时刻导弹的空/地任务类型进行预测,随后根据导弹攻击效果在线评估信息,利用Skyline查询算法将决策空间缩小至非劣解目标集合,再利用级别不劣于关系克服了传统多属性决策存在的属性之间的完全补偿关系,设计了求解导弹最优攻击目标的决策算法。从而完整的解决了导弹攻击过程中任务决策的问题。并经过仿真实验验证了所建立系统的良好性能。

参考文献：

[1] 张冬青,蒋琪.世界导弹武器装备与技术5年发展回顾与展望[J].战术导弹技术, 2016(1): 1-8.

ZHANG D Q, JIANG Q. Reviews and outlooks of global missiles evolution in 5 years version[J].Tactical Missile Technology,2016(1):1-8.

[2] 周伟,董扬帆.2016年国外巡航导弹发展分析[J]. 战术导弹技术, 2017(3): 12-17.

ZHOU W, DONG Y F. Development analysis of foreign cruise missile in 2016[J].Tactical Missile Technology,2017(3):12-17.

[3] ZHONG Y, YAO P, SUN Y, et al. Cooperative task allocation method of MCAV/UCAV formation[J]. Mathematical Problems in Engineering, 2016,2016(11): 1-9.

[4] 沈林成, 陈璟, 王楠. 飞行器任务规划技术综述[J]. 航空学报, 2014, 35(3): 593-606.

SHEN L C, CHEN J, WANG N. Overview of air vehicle mission planning techniques[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 593-606.

[5] SIOURIS G M.导弹制导与控制系统[M].张天光,译.北京:国防工业出版社, 2010.

SIOURIS G M. Missile guidance and control systems[M].ZHANG T G Trans.Beijing:National Defend Industry Press, 2010.

[6] 付昭旺, 于雷, 寇英信, 等. 导弹协同制导中末交接班目标截获概率研究[J]. 弹道学报, 2012, 24(4): 31-36.

FU Z W, YU L, KOU Y X, et al. Target acquisition probability in midcourse and terminal guidance handing-off for cooperative guidance of missile[J].Journal of Ballistics,2012,24(4):31-36.

[7] 张大元, 雷虎民, 李海宁, 等. 复合制导导引头开机截获概率估算[J]. 固体火箭技术, 2014(2): 150-155.

ZHANG D Y, LEI H M, LI H N, et al. Estimate of startup target acquisition probability of seeker for missiles with composite guidance[J].Journal of Solid Rocket Technology,2014(2):150-155.

[8] 刘骁,唐胜景,朱大林,等.制导弹药末段目标截获概率研究[J]. 兵工学报, 2015, 36(2): 287-293.

LIU X, TANG S J, ZHU D L, et al. Research on target acquisition probability in the terminal guidance of guided munition[J]. Acta Armamentarii, 2015, 36(2): 287-293.

[9] 顾佼佼,刘卫华,姜文志.基于攻击区和杀伤概率的视距内空战态势评估[J].系统工程与电子技术,2015,37(6):1306-1312.

GU J J, LIU W H, JIANG W Z. WVR air combat situation assessment model based on weapon engagement zone and kill probability[J]. Systems of Engineering and Electronics,2015,37(6): 1306-1312.

[10] 李波,崔四杰,高晓光.空地一体化多任务导弹攻击模式研究[J].电光与控制,2014,21(12):5-9, 56.

LI B, CUI S J, GAO X G. Research on attack mod of air-ground integrated multi-tasking missile[J]. Electronics Options & Control, 2014, 12: 5-9, 56.

[11] CRISTIANINI N,TAYLOR J S.支持向量机导论[M].李国正, 王猛, 曾华军, 译. 北京: 电子工业出版社, 2004.

CRISTIANINI N, TAYLOR J S. An introduction to support vector machines[M]. LI G Z, WANG M, CENG H J， Trans. Beijing: Publishing House of Electronics Industry, 2004.

[12] 丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1): 2-10.

DING S F, QI B J, TAN H Y. An overview on theory and algorithm of support vector machines[J]. Journal of University of Electronic Science and Technology of China,2011,40(1):2-10.

[13] AL-RAWABDEH W, DALALAH D. Predictive decision making under risk and uncertainty: a support vector machines model[J]. RAIRO-Operations Research, 2017, 51(3): 639-667.

[14] KHANNA D, SAHU R, BATHS V, et al. Comparative study of classification techniques (logistic regression and neural networks， SVM) to predict the prevalence of heart disease[J]. Survey of Ophthalmology, 2015, 38(3): 316-317.

[15] UMA S, SUGANTHI J. An intelligent and dynamic decision support system for nonlinear environments[J]. International Journal of Intelligent Information Technologies, 2017, 8(4): 43-61.

[16] 史峰,王辉.Matlab智能算法30个案例分离[M].北京:航空航天大学出版社,2011.

SHI F, WANG H. 30 cases for Matlab intelligence algorithms[M]. Beijing: Beihang University Press, 2011.

[17] BORZSONYI S, KOSSMANN D, STOCKER K. The skyline operator[C]∥Proc.of the 17th International Conference on Data, 2001: 421-430.

[18] LEE J, IM H, YOU G W. Optimizing skyline queries over incomplete data[J].Information Sciences,2016,s361-362:14-28.

[19] MA Z, SHENG L, XU Y, et al. QBSQ: a quad-tree based algorithm for skyline query[C]∥Proc.of the International Conference on Computer Science and Software Engineering, 2008: 435-437.

[20] 夏淑媛.一种基于Skyline Query的多目标优化方法[D].兰州:兰州大学,2012.

XIA S Y. An approach for multi-object decision making based on skyline query[D]. Lanzhou: Lanzhou University, 2012.

[21] LIN B S, FAN Y B. An improved method for solving multi-attribute problem in transportation mode decision making process[J]. Advanced Materials Research, 2014, 1030-1032: 1961-1965.

[22] 刘新科, 王威, 谭乐祖. ELECTRE I多属性评估方法在防空威胁评估中的应用[J]. 兵工自动化, 2011, 30(7): 19-22.

LIU X K, WANG W, TAN L Z. Application of ELECTREⅠmultiattribute block assessment in air defence threat evaluation[J]. Ordnance Industry Automation, 2011, 30(7): 19-22.