浅谈如何帮助小学生培养空间观念

江苏淮安市富士康实验小学（223001） 蔡振华

空间观念是几何课程改革的一个核心概念。空间观念提升是一个包括观察、想象、比较、综合、抽象、分析，不断由低到高向前发展的认识客观事物的过程。那么如何帮助小学生培养空间观念呢？

一、观察：变换角度，有序观察

观察是任何课程学习的首要环节。善于观察是学习能力强的重要表现。要培养和发展学生的空间观念，教师要引导学生进行多角度的观察，观察时要注意有序性。

在进行常见几何体教学时，我们该如何指导学生对几何体进行观察呢？有经验的教师一定会这样来进行指导：对于图1中的三个几何体，请分别从正面、左边、上面来进行观察，分别画出它们的正视图、俯视图和左视图。

图1

学生通过观察会发现长方体的三视图分别是一个大的长方形和两个小的长方形；圆柱体的三视图是两个一样的长方形和一个圆；圆锥体的三视图分别是两个三角形和一个圆。（如图2所示）

图2

通过多角度和有序的观察，学生从立体图形获得了丰富的平面图形，反过来平面图形的异同也加深了学生对立体几何图形的理解，提升了学生的空间观念。

二、操作：学会画图，自我释疑

（1）要培养学生作图的行为习惯，良好的作图习惯为正确作图打下了坚实的基础。例如，课前让学生准备齐全的作图工具，养成正确的作图姿势，注意作图工具的正确使用，等等。

（2）要遵循学生心理发展的规律，由浅入深、循序渐进地培养学生的作图能力。

从中低年级开始，从简单题入手，培养学生基础的作图能力；要帮助学生厘清思路，确定标准量，画好第一根线。在这个过程中，教师要耐心指导和示范，巧妙点拨，提高学生的作图技巧。教师可以指导学生找准相关的数量关系，然后跟着教师一步一步来画，也可以画出示范画，让学生仿照着重新画一遍。学生掌握了一定的画图技能后，教师就可以放手让学生自己去画，教师只进行适当点拨，并让学生讲清这样画的理由。

（3）让学生多读题、研题，理解题意后，找准对应的数量关系，得心应手地用图解题。作图时首先要提醒学生认真审题，所作图形要与题中所给的条件相吻合。其次，图中线的长短要和对应数值的大小基本一致。最后，图形要尽量画得美观大方，结构合理，具有一定的艺术性，能为解题提供直观的思路。

三、变式：变化形状，变化位置

变式，顾名思义就是变换事物的形式，而本质属性保持不变，通过变化外在形式可更为深刻地体现事物的本质属性。运用变式教学不但能够培养学生思维的深刻性，还能够有效调动学生学习的主动性和积极性。

例如，在教学角的时候，要让学生正确认识角的大小就可以用变式的方法来进行教学。

图3

图3中在箭头左边的是三个角度大小相同的角，但是它们有的边长不同，有的方向不同。箭头右边则是把它们重合后呈现的状态。重合后发现这三个角的度数是一样的。这样学生就会发现，在角中边长、方向等都是形式要素，角度的大小才是本质要素。角的大小是由角两边开合的程度来确定的。

上述案例中教师通过变式教学，有目的、有意识地指导学生在“变”的现象中发现“不变”的本质，从“不变”的本质中探究“变”的规律，帮助学生将所学的知识融会贯通，从而让学生获得学习的快乐。

又如，在学习三角形的面积时，确定三角形的高是关键。教学中，教师也可运用如下变式教学。

图4中的三角形的三条边从左往右分别是AB、AC、BC，在求三角形面积时，它们都可以作为底边，然后画出各自对应的高，图中 h1、h2、h3分别是它们对应的高。虽然这些高的长短不同，位置各异，但是它们的本质就是高的定义——从三角形一个顶点向它的对边作一条垂直线段。正因为这个本质不变，所以在同一个三角形中，不管选择哪一条边来求面积，都是正确的。

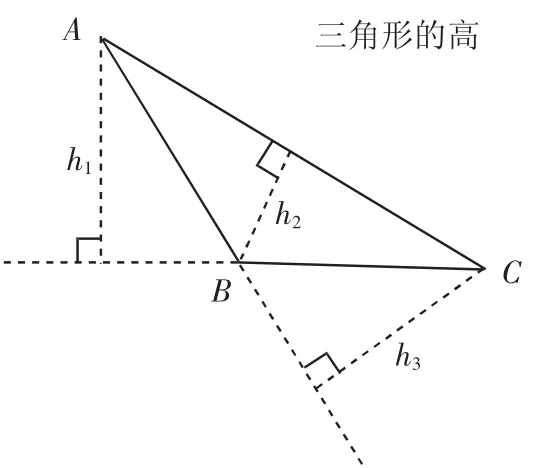
图4

四、辨析：同中见异，异中求同

辨析作为教学的一种重要手段，在各科教学中被广泛运用。通过辨别和分析，学生对于知识的理解更为深刻，对于模棱两可、似是而非的知识点也能更为精确地把握。因此在培养学生空间观念时，教师应想方设法创设情境，让学生在辨析中得到发展。

例如，在学习三角形边长的关系时，就可以设置题目“等腰三角形的两条边分别是3cm、6cm，那么它的周长是多少？”指导学生进行辨析。

上面这个题目，不少学生认为有两个解，分别是12cm，15cm。其实这是错误的。教师可以给学生提供另外一组数据，把其中的3cm换成3.1cm，这样两种解就都对了。这是为什么呢？这时候就要引导学生进行辨析，指导学生在脑海里想象或者在草稿纸上作图：在解答三角形边的长度问题时，一定要注意三角形的三边关系，即任意两边之和要大于第三边，任意两边之差要小于第三边。只有满足这两个条件，三角形才能够成立。原题中，3cm如果作为三角形的一条腰，那么另外一条腰也是3cm，这样两条腰之和无法满足大于第三边（6cm）的要求，因此三角形不成立。把3cm改成3.1cm，虽然只是一个小小的改动，却是一个关键因素的变化，改动后就可以满足三角形任意两边之和大于第三边的条件，因此改题后就有两种答案了，分别是12.2cm和15.1cm。

通过对两个题目的比较，学生在学习和思考的过程中加深了对三角形三边关系的认识，理解了三角形三边关系的定理。同时因为在脑海里想象或者在草稿纸上作图，很好地培养了学生的空间观念。

辨析除了可以采用同中求异的方法之外，还可以采用异中求同的方法来进行。

例如，（1）等腰三角形的两条边分别是3.5cm、6cm，那么它的周长是多少？（2）等腰三角形的两个内角度数之比是2∶5，则内角度数是多少？

上面两个题目，表面上看，一题告诉了两边的长度，另一题则告诉了内角度数比；一题求周长，另一题求内角度数，基本上都不同。但仔细看，它们都是等腰三角形，边角的关系都满足等腰三角形的性质，另外还有一个隐藏的条件就是三角形的三边关系。第一题满足三角形三边关系，因此有两个解。第二题通过等腰三角形等腰对等底的性质也可以得出两个解。通过异中求同不难发现，在不同的外在条件中往往隐含着相同的内在本质。异中求同使学生的几何空间观念得到了进一步的提高。

当然，培养学生的空间观念还有许多的方法，在此就不一一赘述了。