学生审题错误的原因及解决策略
2018-06-06安徽宁国市西津小学242300汪清芬
安徽宁国市西津小学(242300) 汪清芬
要正确解决数学问题,审清题目是前提条件,也是解决问题的基础。审题能力是获取信息、分析和处理信息的一种能力。教师必须高度重视对学生审题能力的培养,让学生通过不断的学习、积累,在实践中提高审题能力,进而独立正确地解答数学问题。为此,我们要找出学生常见的审题错误的原因,然后对症下药,引导学生正确审题。下面我结合自身的教学实践经验对此略抒己见。
一、读题不细
有些题目会故意设置一些小障碍,如果学生读题马虎,很容易会忽视这些小障碍的存在,而直接套用公式,导致解题错误。
例如,一个长方体纸箱,长1米,宽8分米,高5分米,求它的体积。一些学生直接根据长方体的体积公式列式:1×8×5=40(立方米)。但是题给信息中长的单位是“米”,而宽和高的单位却是“分米”,学生忽视了这一点,自然会出错。
解决策略:让学生养成细心读题的习惯,学会发现题目中的小障碍并予以化解,从而正确地解答问题。
以上题为例,我先让学生默读题目,再让学生说说了解到了哪些信息。学生会说:“一个长方体长1米,宽8分米,高5分米,求长方体的体积。”我提示学生把这道题再默读一遍,重点关注题目中的长度单位。学生通过细心读题,从题目中获取有效信息,了解到题目中的小障碍是“单位不统一”,然后我引导学生进行分析:要求出它的体积,第一步该干什么?学生回答:“换算单位,把单位变统一。”最后顺利解决问题。
又如以下判断题,在学生解题前,我要求学生必须先把题目默读两三遍,捕捉题目中可能出现的小障碍,再做出判断。
1.两个体积单位间的进率是1000。( ×)
(障碍:必须是“相邻的”)
2.两个三角形能拼成一个平行四边形。( ×)
(障碍:两个三角形必须“完全一样”或“一模一样”)
3.把一条线段分成7份,其中2份就是2/7。(×)
(障碍:必须“平均分”)
二、读题不全
小学生由于他们这个年龄段的心理特点,使得他们往往只注意运用直白的、显而易见的解题条件来解决问题,而对于那些看似不起眼、实则很重要的条件却视而不见;或者缺乏足够的读题耐心,粗略扫一遍题目,觉得似曾相识,就直接套用以前的解题经验,而忽视重要的解题条件,自然解答错误。
例如,同学们在田径场100米跑道(直道)的一侧植树,每隔4米栽一棵,两端都要栽,一共要栽多少棵?学生忽视了“两端都要栽”这个条件,直接列式:100÷4=25(棵),当然会出错。
解决策略:审题时,引导学生一字不漏地读题,找出题目中的所有条件,用笔圈起来,并充分理解条件的内涵,从而正确解决问题。
本题,我先让学生圈出题目中“一侧植树”“两端要栽”等关键词,让学生读一读,然后再按要求解决问题:距离÷间隔长度=间隔数(全长÷每段长=段数);间隔数(段数)+1=棵数。
三、读题不深
有的数学题会有一些干扰因素,即多余条件,学生如果读题时不够深入,思维就会被扰乱,导致解答错误。如,小明家装潢时买了一卷电线,长100米,电工师傅第一次用了20米,第二次用了15米,一共用去了多少米?学生未深入读题,想当然地认为肯定是求还剩多少米,于是列式100-20-15=65(米)。本题中100米是个多余条件,学生只有排除它的干扰才能正确答题。
另外,有的数学题的条件隐含在某个概念或某个词中,读题不深入就很难发现,自然会出现解题错误。
解决策略:让学生静下心来读题,深入理解题意,抛开多余条件,找出隐含条件,排除干扰,从而正确解题。
四、考虑不周
课程标准指出:“从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。”可事实上,学生在审题时往往不联系生活实际,对问题考虑不周,因此导致错误。
例如,一个长方体游泳池长8米,宽6米,高2米,为了美化和安全,需要在游泳池的里面贴上边长1分米的正方形瓷砖,一共需要多少块?
有的学生按长方体6个面的面积来计算:
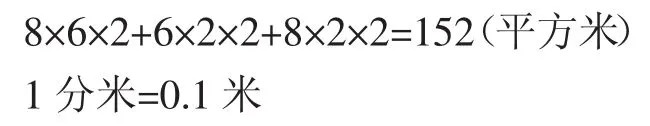
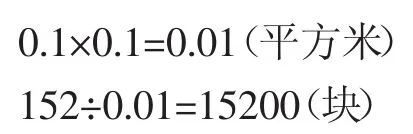
这样解题当然错误,因为生活经验告诉我们,游泳池的“顶”是不需要贴瓷砖的。
解决策略:数学来源于生活,又应用于生活,可以说数学与生活联系紧密。因此,在解决问题时我们要引导学生读题,然后和学生一起联系生活实际进行具体分析,避免掉入题目设置的陷阱里。
又如,用铁皮做一个高4米的长方体烟囱,底面是个正方形,边长5分米,需要多少平方米的铁皮?
学生读题后,教师要引导学生联系实际说说烟囱是干什么用的,需要求几个面。学生只要了解了生活中烟囱的作用,就能正确地解决问题。
五、术语不明
许多数学题会用到数学术语。数学术语是反映数学关系的专业用语,具有很强的学科性,比较枯燥,有的只有一字之差,意思却截然不同,如果不去仔细推敲,极易混淆。
如用2.4除以1.2的商去除它们的差,商是多少?
部分学生出错的原因是没有推敲数学术语“除”的含义,列式成:(2.4÷1.2)÷(2.4-1.2)。
解决策略:在解答文字型应用题时,引导学生仔细推敲关键的数学术语,通过反复琢磨数学术语的含义,准确找出题中的数量关系。
本题中的关键术语是“除”。“除”这个关键词决定着什么量做被除数,什么量做除数,稍有不慎就会把数量关系弄错。我引导学生着重推敲理解“除”后,数量关系也就理顺了,问题便迎刃而解。根据题意,其数量关系应该是“差除以商”,正确列式是:(2.4-1.2)÷(2.4÷1.2)。
又如,(1)工程队修一条路,已经修好全长的2/3,距离中点12米。这条路全长多少米?(2)工程队修一条路,已经修好全长的2/3,距离终点12米。这条路全长多少米?
这两道题的区别在于,条件中的“中点”与“终点”不同。因此,解题前我引导学生圈出“中点”与“终点”,并让学生读一读,着重理解它们的含义,最终正确解决问题。
总之,教师一定要培养学生获取信息、分析和处理信息的能力,让学生学会仔细、全面、深入地审题,只有学生的审题能力得到了提高,才能正确解决问题。
