分数的意义教学疑难问题“诊治”

江苏盐城市第一小学教育集团聚亨路校区（224000） 谷文燕

“分数的意义”一课通过分鸭梨的活动，让学生认识分子、分母的不同含义，进一步理解抽象意义上的分数。对于本节的教学，有许多经典课例：有的以剖析单位“1”为主线进行教学；有的在学生充分自学的基础上，以民主辩论的形式开展教学；有的以分数单位的辨析来构建分数的意义……笔者在研究这些经典教法的基础上，博采众长，同时对本课存在的疑难问题进行了“诊治”。

一、“望”：病例观察

以下是某位教师教学苏教版教材三年级下册“认识一个整体的几分之一”的片段。

教师提问：“光头强准备了一箱鸭梨，平均分给熊大和熊二，每只熊各分到这箱鸭梨的几分之几？”

学生回答道：“每只熊能分得这箱鸭梨的二分之一。”

教师再次提问：“光头强会在包装箱里放多少个鸭梨？请大家拿出‘包装箱’（磁性小黑板）和‘鸭梨’（磁性黄色剪纸），我们来帮可爱的熊熊公平分配。”（教师指名选择2个鸭梨、4个鸭梨和6个鸭梨的学生上台贴图演示，并汇报交流）

此时，有个学生说道：“老师，包装箱里只放3个鸭梨，行吗？”“是啊，”其他学生也附和道，“包装箱里的鸭梨数可以是5、7、9……吗？”

教师反问道：“如果是这样，能平分吗？”（学生发现无法实现平分）教师提示：“其实，无论多少个鸭梨，都能平均分成2份，每份都是总量的1/2。”……

在课堂尾声，教师用课件显示一条有10个间距的线段（如图1），提问：“你能找出1/2吗？”

图1

学生一开始得出这样的结果（如图2）。

图2

教师继续启发：“还有其他的分法吗？”在教师的启发下，学生得出其他形式的1/2（如图3）。

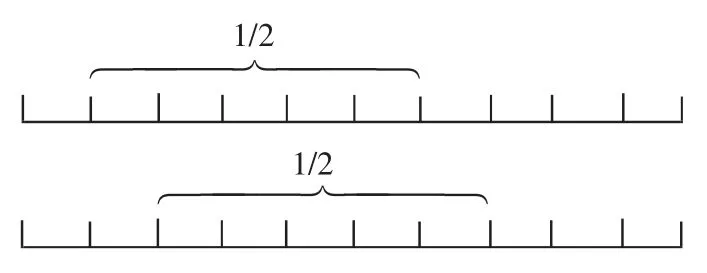
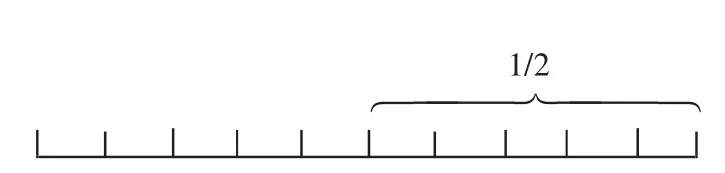
图3

最后，有位学生这样表示1/2（如图4）。

图4

教师追问：“能说一下你的思路吗？”

学生回答道：“这个点是线段的中点，它到线段两端点的距离为总长度的一半。”教师借机在他的图上添加括号，擦除中间的“1/2”，新添两个“1/2”（如图 5）。

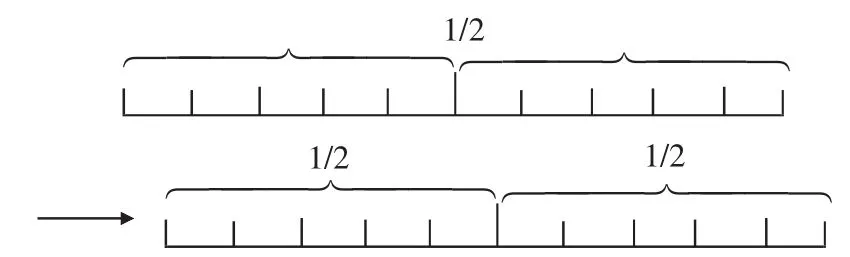
图5

教师总结：“事实上，这位同学的做法是合并了刚才两张图。”

二、“问”：病历记录

课后，笔者采访执教者：“预设时，你有没有预料到学生会想到奇数分不开的情况？”对方斩钉截铁地回答：“想到了，但反馈时可以避开突发提问，只谈偶数的情况。”“那如果鸭梨数真是一个奇数，您觉得可以对半分吗？”笔者接着问。“这个……教材里没有这样的预设。”此时，执教者有点后悔：“放开了搞不好就会关不上闸。”……之后，笔者采访一些学生：“你们能把3个鸭梨平分成两份吗？”有学生这样说道：“先每人分1个，再把余下的1个切成两等份，一人一半，合起来每人分到手一个半鸭梨。”……最后，笔者提问那个找出中点表示1/2的学生。“老师的解释你能懂吗？”这位学生一会儿摇头，一会儿点头，也说不清楚……

三、“切”：病理诊治

上述试课是苏教版教材三年级下册“认识一个整体的几分之一”的新授课，可以说是由“平分个体”到“平分整体”的过渡，从分数的“数量比”过渡到“份数比”，是认知形态的升级，也是分数教学中的难点。

在苏教版教材中，“认识一个物体的几分之一”，从分物体的情境图（图6）中导入，其中蛋糕的分配结果是“1/2个”，再将具体数量对比换算成“1/2”，其中“1/2”成了指代局部与整体之间比例关系的一个数。

图6

由此开始，教材专门研究表示比例关系的分数，久而久之，学生一看到分数就会下意识地想到“什么（占）什么的比例”，如试教课例的尾声，教师提问：“你能找出1/2吗？”本意是“能标出线段的1/2吗？”只是忽略了单位“1”。教师初衷是让学生用多种方法表示整条线段的1/2，属于没有固定答案的开放性问题。事实表明，学生可以找出不同的1/2。值得一提的是，有一位学生用中点表示1/2，别出心裁，这尚属直觉，他想要表达的仍是“此处将线段一分为二，每一份是这条线段的1/2”，这也是教师需要借题发挥的地方。如果他想表达的是“唯有这个点才能分出1/2条线段，所以用1/2标识”，那么教师恰好借题发挥，对素材做一些改装：变线段为数轴（如图7），只出现正半轴，以此为载体，实现分数的“比例”含义向“商值”含义的过渡。

图7

在此意义上，正是“你能找到1/2吗？”这句不够严密的话语提供了开放性，释放了自由思考空间，教师因势利导，就可以扩充分数的内涵。教学“认识一个整体的几分之一”时，虽然只需要提取总份数和取得的份数，然而学生很难排除具体量的干扰，总念着每份数。于是，学生才会拿奇数情况来“刁难”老师。

对这个问题，执教者之所以无言以对，是因为无法“平均分”是教师的一厢情愿，然而学生自有“高招”——“先每人1个，然后切分余下1个”。当然，教师也可以引导学生这样平分：把所有鸭梨都分成两半，得到6个半块，再来分配“6个半块”这个整体，刚好平分成2份，每份3个半块，合起来就是1个半鸭梨。由此可见，3个鸭梨也可以平分成2份。

如果说“3”这个数据特殊，容易分成2份，容易想到“先分整个鸭梨，再切分单个”的方法，也能理解“先切分全部再平分”的方法，那么对“把3个鸭梨平分成4、5份，每份是多少？”的问题，学生就犯难了。当然，学生也有可能受到启发，想到“先把每个鸭梨切分成若干份，再分配”。可是这样做很麻烦，教师和教材都刻意回避了这一问题。

上述课例，教师的提问“光头强会在包装箱里放多少个鸭梨？”从课后访谈来看，教师提出这个开放性问题前，虽然预料到了各种突发状况，也预留了后手——“反馈时只选偶数情况”，这种选择性理答，是一种“假开放”，所以教师事后后悔不迭——“放开了搞不好就会关不上闸”。其实，这样的“开放”很宝贵，既顺从了学生的第一反应，又展露了学生的初始状态，只要教师尊重学生、相信学生，就可以找开开放性问题的闸门，丰富分数的内涵，所以教师完全不必为收不拢而拒绝“开放”。