一道习题引发的“洪荒之力”

安徽马鞍山市四村小学教育集团（243000） 唐 明

随着里约奥运会上游泳运动员傅园慧的一次采访，“洪荒之力”迅速成为网络热词。在我的数学课堂上，因为一道习题引发的讨论、思考和启示，也让学生脑洞大开，使出了“洪荒之力”。

习题：

图1

【题意简析】在日常生活中平均分物体，结果无非是两种情况：一种是恰好分完，没有剩余；另一种是平均分后还有剩余。新人教版教材二年级下册第六单元“有余数的除法”要解决的问题大多是对单一物体的平均分，而课本70页的第8题是一道综合题，需要学生综合考虑3种花的情况，这对二年级学生来说有一定难度：要以3种花中要求的枝数所能扎的束数最少的那种花为标准才能确定答案。此题有利于培养学生思维的全面性与灵活性，使学生能辩证地思考问题。

【镜头回放】教学时，我预设到这道题对学生来说很难理解，于是让学生在审题后交流思路。生1第一个举手：“我打算先把这些花的总数算出来，再把每束花的枝数算出来，然后用总数除以枝数。”其他学生有的点头表示同意，有的保持观望。生2小声地嘀咕：“7+3+2=12（枝），除数是12，我们没学过啊？”生3表示反对：“我觉得应该分开算，把玫瑰、百合、郁金香分别能扎成几束先算出来再比较。”两种方法都有支持者，但谁也没有足够的理由说服对方。于是我让学生先自己试试看。在巡视的过程中，我发现大部分学生选择了生3的算法，小部分学生仍在纠结。生1很快就算出了答案：22+16+10=48（枝），7+3+2=12（枝），48÷12=4（束）。他的答案刚好给生2的想法一个“回击”：“你不是说除数是12，没学过就不能算吗？我能计算是不是就对呢？”我把生1的解题过程进行展示，并提问：“最多能扎成4束，这样做行吗？怎么验证？”“画图！”有几个学生不约而同地说。学生用图形表示各种花，然后按照要求圈出相应的枝数后，发现最多只能扎3束。（如图2）

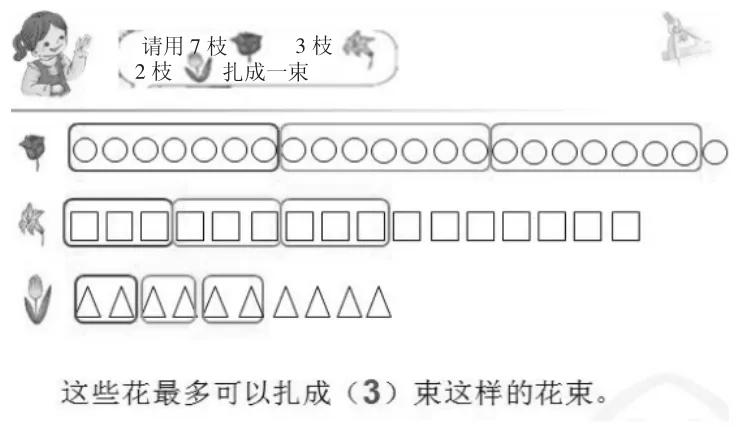
图2

“为什么算出来的是4束，圈出来的是3束呢？”我把问题抛给学生，并引导他们观察每种花剩下的枝数“1+7+4=12（枝）”，而每束花需要的枝数恰恰也是7+3+2=12（枝）。终于真相大白了，“玫瑰只剩下1枝，根本不够扎一束。”“虽然多扎了一束，但不符合要求。”学生七嘴八舌地议论开来。“你们觉得利用画图来分析这道题是不是更清楚？”学生纷纷点头。“我有不同的想法。”生4从不人云亦云，“虽然画图很清楚，但我们画了几十个图形，太麻烦了。如果花的枝数更多，那怎么画？老师不是说数学语言要简洁吗？”我紧接着说：“你们有没有办法让画图变得更简单呢？”大家都沉默了，生5突然眼前一亮，脱口而出：“线段图！”学生在二年级上册就接触过线段图，所以当听到生5的想法后，也有不少学生能根据题意画出线段图。（如图3）

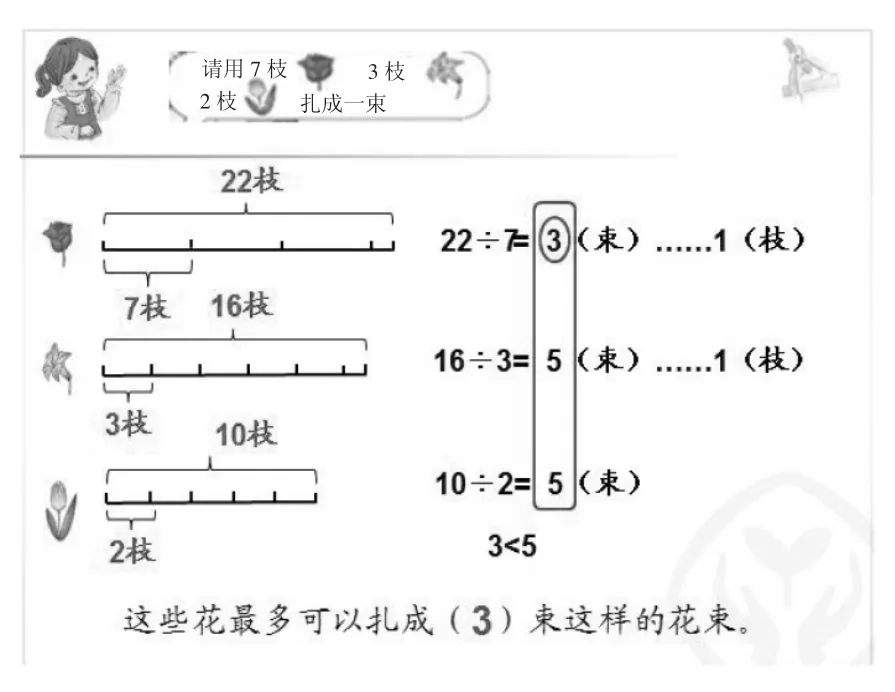
图3

在解决问题的过程中，“回顾与反思”这一环节是不能省略的。学生以结果作为已知条件，验证后发现：按照要求只能扎成3束花，虽然每种花都有剩余，一共剩余12枝，每个花束也需要12枝，但只是数量上相等，花的品种却不符合要求。（如图4）

图4

【精彩继续】课堂练习中有一道类似的题目（如图5），我要求学生在随堂本上完成，这样会有足够的空间让他们展示个性化的思考过程。

图5

很快，学生就想到了将抽象的数学语言与形象的图形有机地结合起来。（如图6-1、6-2）

图6-1

图6-2

虽然只是围绕这一道习题做文章，我却觉得时间“浪费”在这很值得。我们往往认为教师的讲授能节省教学时间，但学生自己习得知识的过程却更加宝贵。在结束学习后，学生分享了许多经验：这类题目可以命名为“混合包装”，首先要看清关于包装的要求，可以通过摆出实物图、画出线段图等来理解题意，列式时要分类计算，确定答案时以商的最小值作为标准，最后还要将结果作为条件进行验证。更有学生总结出了解题四部曲“理解要求、数形结合、分类计算、确定答案”，真正学习并体会到要解决一个数学问题所要经历的步骤。

当天我安排了两道数学作业题：

1.用2个鸡蛋和3片吐司就可以做出一份三明治，现在有10个鸡蛋、10片吐司，能做出几份三明治？

图7

学生在解决“做出几份三明治”这一问题时还发现：在鸡蛋和吐司总数相同的情况下，只要算10÷3就能确定答案。因为3>2,被除数相同，除数越大商就越小，只需要将商的最小值作为标准就能得到答案。

2.自编一道有关混合包装的题目。

在自由编题的过程中，学生的想法更加鲜活。在他们的眼里，包装的对象十分宽泛：

图8-1

图8-2

图8-3

图8-4

新教材从一年级开始就出现了大量的情境图，二年级则通过条形图呈现信息，三年级正式引入线段图……这样的编排符合学生对画图策略的认识、理解和运用的过程。然而在实际教学中，我们常常只把画图策略看作教师分析问题的工具，忽略了它也是学生解决问题的法宝。

数形结合，是一种数学思想方法，也是方法上的思想。虽然刘加霞在《数形结合思想及其在教学中的渗透》一文中提出“借助直观模型理解抽象的数量关系并不算是严格意义上的数形结合”，但她也认可这是数形结合的雏形。“有余数的除法”重点在于引导学生在解决问题时注意借助直观帮助理解题意、分析数量关系。但在实际学习中，很多学生解决问题时往往忽视对题意的理解，虽然能做对题，但不见得真正懂了，有时题目稍加变化，就无法应对。对于低年级学生来说，理解题意的过程，往往需要借助直观。教师在教学时应充分借助直观，让学生学会利用图形来描述和分析问题，从而清晰地“看到”数量关系，找到解决问题的思路，并最终得到解决问题的方案。

考虑到学生不同的认知水平，教师可以先从实物图开始，再过渡到几何符号表示的图，最后抽象成线段图。这样就是将多种表征结合起来，借图促思，据图说理，把复杂的数学问题变得简明和形象。画图策略的渗透不能停留在“教师画，学生看”的状态，而是要提升到“学生画，学生用”的水平。这实际上是一个“数”与“形”互相转化的过程，通过引导学生把数学问题中的运算、数量关系等与几何图形或图像结合起来思考，使“数”与“形”优势互补、相辅相成，就能使学生的逻辑思维和形象思维完美地统一起来。

在解决问题的过程中，画图不是最终目的，学生把文字转化成图画，再把图画转化成思维，由数思形、见形想数，有助于学生把握数学问题的本质。只要学生能不断地运用画图策略，就能提高自身的数学学习能力和解决问题的能力。