Flocking control of a fleet of unmanned aerial vehicles

Adel BELKADI,Zhixiang LIU ,Laurent CIARLETTA ,Youmin ZHANG ,Didier THEILLIOL†

1.CRAN,University of Lorraine,Nancy,France;

2.Department of Mechanical,Industrial and Aerospace Engineering,Concordia University,Montreal,Canada;

3.Lorraine Research Laboratory in Computer Science and its Applications(LORIA),University of Lorraine,Nancy,France

1 Introduction

The last decade has seen an increasing number of unmanned aerial vehicles(UAVs)applied to a variety of applications,such as forest health/fire surveillance[1,2],search and rescue[3],natural resources exploration[4],environmental surveillance[5],and military missions[6].As an important type of UAV,unmanned quadrotor helicopter(UQH)has also been dedicated significant investigations due to their numerous advantages including decreased operation complexity,affordable development cost[7],and improved maneuverability[8].These characteristics have contributed tremendous benefits to avariety of applications demanded by many universities,research institutes,commercial entities,and military[8].

In order to greatly enhance the capabilities of UQHs against system failures,improve their efficiencies,and extend their coverage of surveillance and measurement applications,current research on UQH has already gone beyond single system.Inspired by the study of biologists on the flocking phenomenon of animals in nature,such as schools of fish,swarms of insects,herds of quadruped,and flocks of birds,Reynolds[9]has introduced the following three heuristic rules for the flocking control of a group of agents[10]:

1)flock centering(cohesion):stay close to nearby agents;

2)collision avoidance(separation):avoid collisions with surrounding agents;and

3)velocity matching(alignment):match velocity with neighboring agents.

These three rules have been considered as the basic elements of developing the theoretical framework and control strategies for the flocking control of multiple agents systems(including heterogeneous numbers and categories).

The flocking control of multiple UQHs for a diversity of applications,including environmental surveillance,search and rescue,and natural resources exploration,has likewise attracted much attention from researchers around the world.On the early stage of flocking control development,several distinct flocking models have been developed.The first flocking model is proposed in[9].Then,the Cucker-Smale model is constructed in[11],while[12]develops the Vicsek model.Later on,an improvement to Vicsek model is made in[13].Following these models,numerous relative flocking control methods have also been investigated.Whereas these works solely concentrate on the alignment problem,while other rules of flocking control are not well studied.To improve the performance of flocking,further investigations are conducted.One research in[10]has combined the alignment rule with an additional repulsive/attractive term for keeping all agents within a desired region,whiletheunified velocityhasbeen matched by all agents.In addition to that,numerous studies have also extended the Cucker-Smale model[11]to maneuvre a fleet of unmanned vehicles[14].In[15],a repulsive force is incorporated in the flocking control design to maintain the safety distance among agents,a rigorous proof is provided to guarantee the collision avoidance capabilities of agents.Works in[16]and[17]extend the Cucker-Smale model by introducing additional interaction terms among agents for the purpose of achieving both collision avoidance functions and tighter spatial configurations.Other relative works on this subject are carried out in[18,19]which derive a decoupled control term based on a potential function;this term is devised to achieve the separation and cohesion among agents,together with using the velocity consensus control rule,both formation-keeping and collision avoidancecan be guaranteed.However,the above-mentioned approaches tend to be quite dangerous in the presence of low accurate measurements or actuator and sensor faults.Furthermore,most of the existing flocking control methodologies are designed and validated only on a simple system with double integrator dynamics without consideration of system uncertainties and nonlinear dynamics.These adverse effects may dramatically deteriorate the performance of flocking,as well as cause significant oscillations[20]and even divergence.

In order to surmount the aforementioned challenging issues,this paper proposes a new flocking control approach which is an extension of authors’previous work summarized in[21].Different from the method adopted in[18,19],the solution proposed by this work is to consider all agents as a group without specifying any distances among them.The proposed method,which is expected to achieve the satisfactory performance(cohesion,separation and alignment)of multiple UQHs,treats the whole system as the following three layers:

1)guidance system(flocking rule)for the translational control design in kinematics level;

2)motion control system for rotational control design in kinetics level;and

3)UQHs systems.

The contributions of this paper can be highlighted as follows:1)design of a new flocking control method and implementation of it on a group of UQHs with nonlinear dynamics to make the proposed method applicable in practice;and

2)it is normally difficult to guarantee the fixed neighbouring distance required by some existing works and model uncertainties and disturbances in practice can cause significant oscillations of agents.

In addition,by using the formation control algorithm with fixed neighbouring distance requirement,it may become quite complicated to satisfy the anticipated formation control performance when the number of agents remarkably increases.However,the proposed flocking control method requires no fixed distance among agents,providing more flexibility to the formation control,especially for the practical implementation.

Therest of this paper is organized as follows:Section 2 introduces the modelling of UQH and some preliminaries of flocking control system design.Section 3 illustrates the design procedure of the presented flocking control system.Section 4 addresses the conducted numerical simulations and their results analyses.The last section summarizes the conclusions and future works.

2 Preliminaries

2.1 Nonlinear model of unmanned quadrotor helicopter

As shown in Fig.1,the UQH is usually operated by four motor-driven propellers which situate at the front,rear,left,and right corners of UQH,respectively,generating their corresponding thrusts u1,u2,u3,and u4.

Fig.1 Schematic diagram of a typical UQH.

Generally,the motion of UQH can be illustrated as follows:

1)identical amount of control signals are distributed to each motor to achieve the vertical translation;and

2)distinct amount of control signals are assigned to the opposite motors to fulfil the horizontal translation[8,22].

For a common dynamical model of UQH in regard to the earth-fixed coordinate system,one can obtain that

Moreover,the following relationship between accelerations and lift/torques can be formulated:

The propeller force and its corresponding pulse width modulation(PWM)signal has the foll owing relationship:

To facilitate the control scheme design,borrowing the ideas of existing research works[8,23],the following model simplification can be obtained as

Therefore,equation(3)can be reduced to

where Kmand ωmare theoretically assumed to be identical for all motors.

The definition of above-mentioned symbols are all included in Table 1 for readers’convenience.

Table 1 Nomenclature(earth-fixed coordinate system).

2.2 Linearization of the unmanned quadrotor helicopter

As UQH’s model is highly nonlinear,translational and rotational motions are coupled,in order to match the dynamics of UQH with double integrator model to enable the design of the flocking control algorithm,Assumption 1 is thereby made for linearizing the dynamics of UQH.

Assumption 1The UQH is assumed to be in a near hovering condition which implies that:1)uz≈m g points toward the vertical direction;2)pitch and roll angles are so small that sinφ≈φand sinθ≈θ;3)there is no yaw angle(ψ=0).

Based on Assumption 1 and equation(1),the new translational and rotational dynamicsof UQHin the similar formulation of double integrators can be achieved as equations(5)and(6),respectively.

1)Translational dynamics of UQH:

2)Rotational dynamics of UQH:

3 Flocking control scheme design

As addressed in Fig.2,the system architecture of the proposed method can be divided into three levels:the high level(translational motion control)guidance system,middle level(rotational motion control)control system,and low level(UQH system)[24].First,based on the mission command and states of formation,the high level guidance system produces the rotational reference command,which is then distributed to the middle level control system for maneuvering the low level UQHs to follow the desired references.

贪污腐败的形式之一是私相授受，一方是政府官员受贿，游说团体的说客们往往就扮演了上门贿赂的脚色。第八、九章的分析对象就是这些活动越趋频繁、势力日渐庞大的游说团体。2007年，美国首都华盛顿有经注册的说客约35 800人。游说这一行，作者称之为“游说业” (the lobbying industry)，2007年向其客户收取的费用总计高达29亿美元。游说业之势力由此可见一斑。

Fig.2 Control architecture of the proposed approach for each agent.

3.1 Modified Cucker-Smale model design

As a widely employed model for flocking control design,the Cucker-Smale model introduced by[11]is also used in this study.In this flocking model,each agent updates its velocity in every sampling time by adding to it with a time-varying value,which is the weighted average of the differences of its velocity with those of its neighboring agents.

Assume a continuous model consists of n agents,xi(t)and vi(t)(i=1,...,n)denote the position and velocity of the i th agent,respectively.The dynamics of flocking model is then defined by

where the weighting function aij(t),which represents the inter-agents distance between agents i and j,can be obtained by

where H ＞ 0,σ ＞ 0,and β ≥ 0 are a given set of system parameters.

The performance of Cucker-Smale model(7)depends on the selection of β,which satisfies the following conditions to guarantee the convergence of flocking:

with

It is worth noting that the convergence of the formation towards a flocking behavior(like a common velocity)can be obtained relying solely on the initial state conditions(x(0),v(0))of theflock if any of the conditions in equation(9)have been satisfied.

In addition to guaranteeing the convergence feature of a flock of agents,it is also critical to ensure the collision avoidance among agents in order to fulfill the desired mission with a safe and satisfactory performance.Reference[15]proposes a flocking control method ensuring all agents converge to an identical velocity,while simultaneously satisfy the demand for collision avoidance.Furthermore,a solid mathematical stability proof is also provided.By borrowing the concept proposed in[15],the flocking model(7)can then be rewritten as follows:

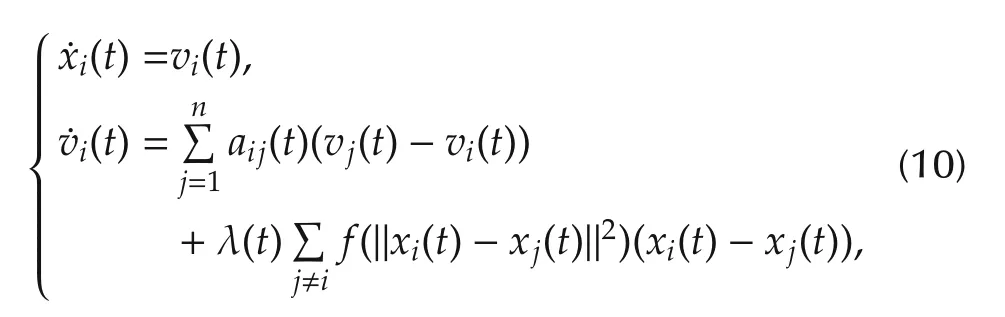
where

λ(t)is designed to moderate the repelling force,while λ(t)=0 indicates that all agents in the flock align at a common velocity,r0＞0 denotes the safety distance among all agents,and the differentiable function f(r)should be subjected to the following conditions:

The first condition in equation(11)is used for ensuring collision avoidance,while the second one is devised for guaranteeing the convergence of flock to alignment.

Thus,it is possible to summarize the three objectives of equation(10)as follows:

·asymptotic velocity convergence of pairwise agents:

·asymptotic formation keeping:

whereand R(n,r0)＞ r0denote the distance between the i th and j th agents and maximum radius of the formation,respectively;and

·collision avoidance among neighboring agents:

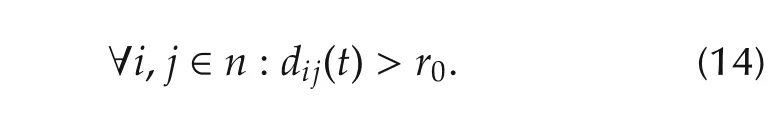
3.2 Translational motion control scheme design

The translational motion control law is designed using flocking theory based on the modified Cucker-Smale model.From equation(5),solely considering the variables related to the operation of UQHs in X-Y coordinate system,one can then obtain the position and velocity vectors for each UQH asandrespectively.The corresponding control input is selected as ui=[gθ,−gφ]T.

Thus,the translational dynamics of UQH can be written as follows:

In order to satisfy the three objectives proposed in equations(12)–(14),in addition to using equation(10)to meet the velocity matching and collision avoidance requirements,additional scheme for keeping the formation within a desired circle to flock centering is still required.Actually,this issue has been widely discussed in the literature,and solid mathematical proof are also provided.To guarantee the cohesion property of fleet with out changing the overall dynamics of flocking model(10)introduced in[15],this study proposes to add abounded attractive force term to equation(10)for constraining all agents within a circle with specific radius.Thus,with this additional term,equation(10)can be rewritten as

where the bounded attractive force termis obtained by calculating the distance between the ith agent and the average positionandwhile functionsatisfies

Functionis calculated by

where Hcis a positive constant.

Equation(17)indicates that the bounded attracting force affects the agent which is outside the specific circle for keeping the desired formation;while the attracting force vanishes when the agent is within the desired circle.

Since the proposed flocking control algorithm is designed based on the linearized models(5)of UQH,while the simulation/experiment is conducted on the nonlinear model(1).It is thereby inevitably required to consider the uncertainties from the model linearizati on and external disturbances without causing much unexpected oscillations and serious performance degradation.In this study,the additional tuning gains are added to the three terms in equation(16)in order to compensate the uncertainties of linearized model and disturbances.Based on this design,the further modified flocking control law(16)becomes

where Kp＞0,Kd＞0 and Ka＞0 represent the user defined tuning gains.

3.3 Rotational motion control scheme design

The linear quadratic regulator(LQR)control methodology,which is well-known and widely applied for a variety of industrial,academic,and scientific research applications,can be a suitable solution for the controller design of single UQH[25].Therefore,in this study,the LQR control scheme is adopted to develop the state feedback control strategy.

Without loss of generality,the linearized UQH model(6)with consideration of merely pitch and roll motion,can be rewritten into the following state-space representation:

where x(t)∈Rnis the state vector,u(t)∈Rmdenotes the control input,A ∈ Rn×n,and B ∈ Rn×m.ω(t)=[g,ωd(t)]Tincludes acceleration of gravity g and bounded external disturbance ωd(t)∈ Rr.In this study,

As an effective mechanism for eliminating the steady state error,the integral term is further introduced into the control scheme design[26].After incorporating this integral term,system(20)can then be augmented as follows:

includes ω(t)and reference signal yref(t).

Sr∈ Rl×pis used for selecting the required system states.

Then,the employment of LQR controller is to design an appropriate control input u(t)to operate the augmented system from any initial state xa(t0)to the equivalent state within an infinite time period.This can be achieved by minimizing the following objective function[27]:

where Q ∈ R(n+l)×(n+l)is a symmetric matrix,and R ∈R(m+l)×(m+l)is a positive symmetric definite matrix.The state feedback gain K is then obtainable by solving algebraic Riccati equations.

Ultimately,the optimal augmented state feedback control input can be obtained as

4 Simulation validation

In order to demonstrate the effectiveness of the proposed flocking control method,numerical simulations on a group of UQH nonlinear models(a total of 12 agents)have been conducted.System parameters of the studied UQH,which are adopted from a real one,are listed in Table 2.

Table 2 Values of used system parameters.

Initially,UQHs in the fleet are allocated with different velocities and distributed in distinct positions.The safety distance of pairwise UQHs is set as 1m.The values for the adopted flocking controller parameters are selected as follows:H=1,β=0.4,Hc=0.1,r0=1m,Kp=0.5,Kd=0.7,Ka=1.7.The control gains for the motion controller is computed as

As shown in Fig.3,the radius of the fleet is first assigned with R(n,r0)=12m,then changed to R(n,r0)=10m and R(n,r0)=8m at the 30th and 60th second,respectively.The result demonstrates that the desired fleet reformation is achieved by the proposed flocking control method.

Fig.3 The flocking movement of the fleet.(a)t=0s,Radius=12m.(b)t=25s,Radius=12m.(c)t=50s,Radius=10m.(d)t=100s,Radius=8m.

Fig.4 displays the velocity histories of all UQHs along the x and y coordinates.It can be observed from Fig.4 that the fleet can converge to the common velocity within around 20 seconds.

To investigate the performance of the fleet of UQHs in a clearer fashion,Fig.5 shows the minimum and the maximum distances between each two agents,these distances are calculated by

From Fig.5,the safety distance 1m between neighbouring agents can always be guaranteed,while the maximum distance for keeping the desired formation is satisfied as well.

Fig.6 shows the average distance difference Φ(t)and average velocity difference Ψ(t)of pairwise UQHs.It clearly shows that the desired formation keeping and velocity matching performance are achieved.The Φ(t)and Ψ(t)are calculated by

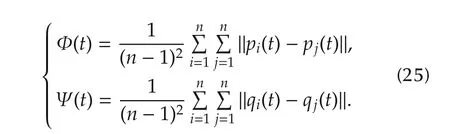
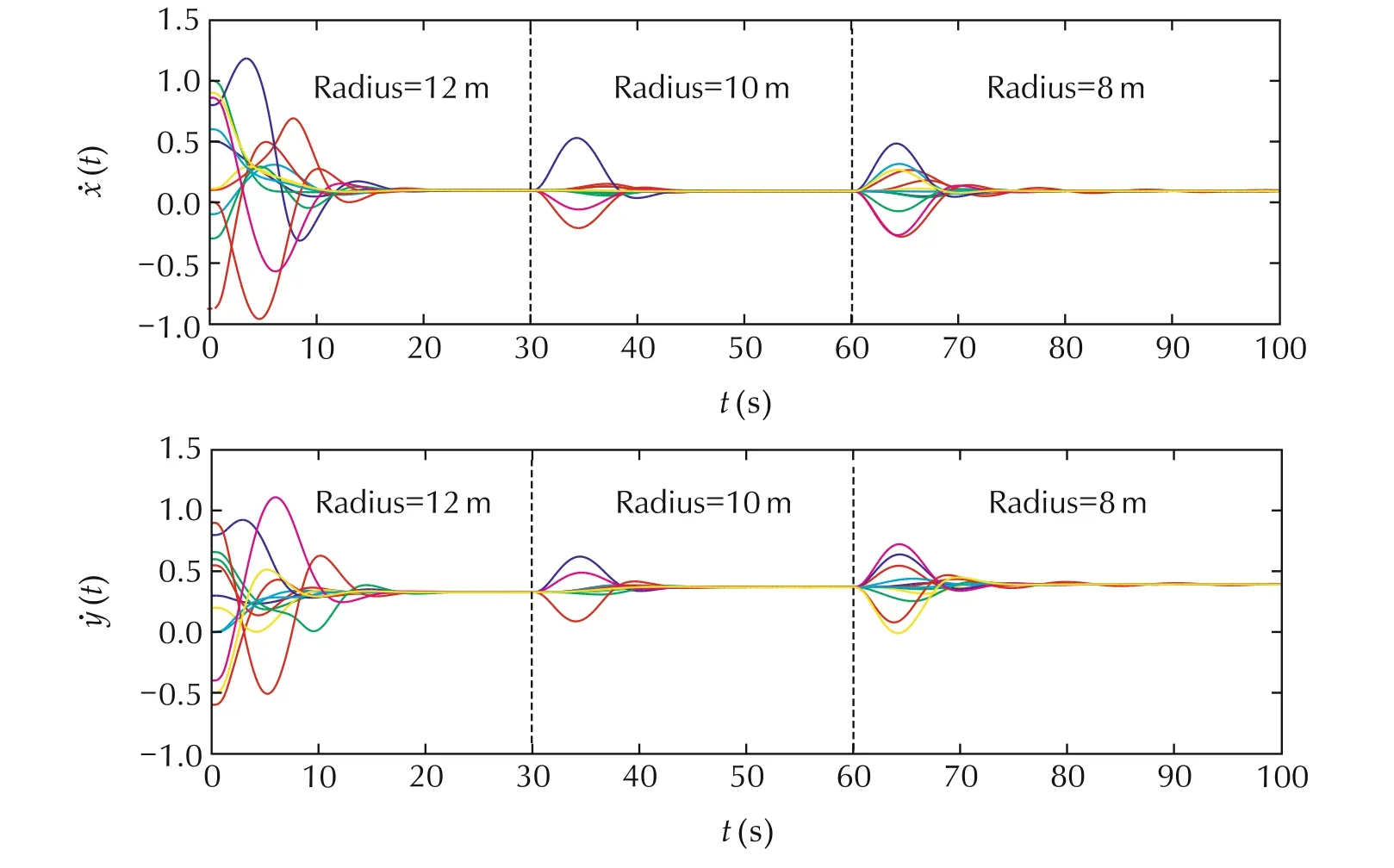
Fig.4 The velocities of all agents.

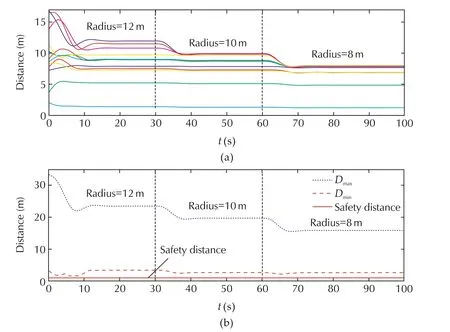
Fig.5 The distances of the fleet.(a)Distances between agents and flocking center.(b)Minimum&maximum distances between pairwise agents.

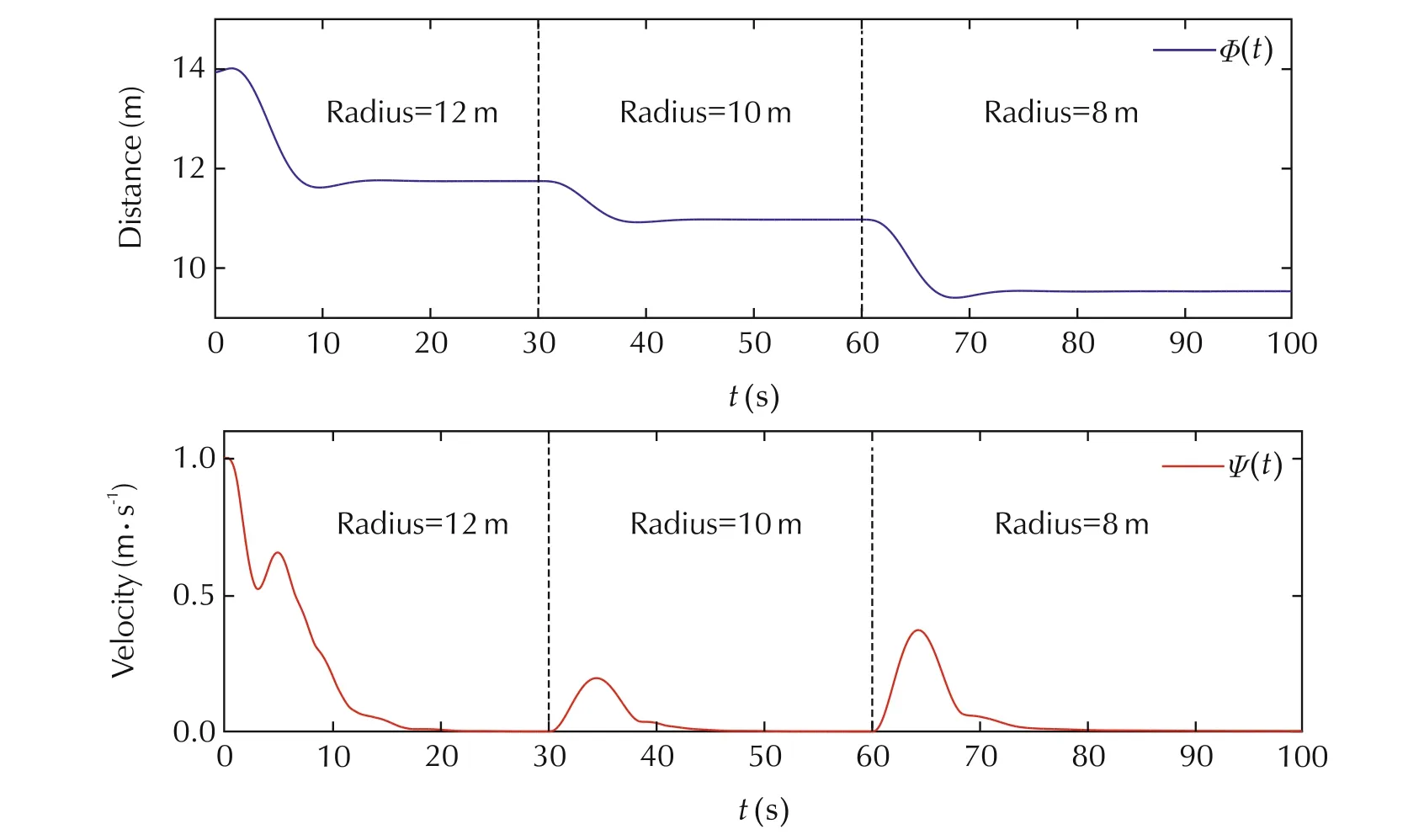
Fig.6 The average distance and velocity differences of pairwise UQHs.

5 Conclusions

This paper presents the development and application of a new flocking control algorithm on a fleet of unmanned quadrotor helicopters(UQHs)with nonlinear dynamics.The three critical characteristics of flocking,the cohesion,separation and alignment have been guaranteed in this work.First,the linearized model of unmanned quadrotor helicopter is demonstrated to be effective for designing both flocking control and motion control algorithms.Then,the satisfactory performance of the proposed method on multiple UQH nonlinear models is achieved in the numerical simulation.

In the future,it is expected to extend the proposed work to considering both sensor and actuator faults in the scheme design to enhance the reliability and safety of the system.Further experimental tests on a group of real UQHs in the authors’lab have also been planned to further validate the proposed method.

[1]C.Yuan,Y.Zhang,Z.Liu.A survey on technologies for automatic forest fire monitoring,detection,and fighting using unmanned aerial vehicles and remote sensing techniques.Canadian Journal of Forest Research,2015,45(7):783–792.

[2]C.Yuan,Z.Liu,Y.Zhang.Aerial images-based forest fire detection for firefighting using optical remote sensing techniques and unmanned aerial vehicles.Journal of Intelligent&Robotic Systems,2017,88(2/4):635–654.

[3]D.Kingston,R.W.Beard,R.S.Holt.Decentralized perimeter surveillance using a team of UAVs.IEEE Transactions on Robotics,2008,24(6):1394–1404.

[4]A.Rango,A.Laliberte,J.E.Herrick,et al.Unmanned aerial vehicle-based remote sensing for rangeland assessment,monitoring,and management.Journal of Applied Remote Sensing,2009,3(1):DOI 10.1117/1.3216822.

[5]J.E.Gomez-Balderas,G.Flores,L.G.Carrillo,et al.Tracking a ground moving target with a quadrotor using switching control.Journal of Intelligent&Robotic Systems,2013,70(1/4):65–78.

[6]J.Escareno,S.Salazar,H.Romero,et al.Trajectory control of a quadrotor subject to 2D wind disturbances.Journal of Intelligent&Robotic Systems,2013,70(1/4):51–63.

[7]Z.Liu,C.Yuan,X.Yu,et al.Retrofit fault-tolerant tracking control design of an unmanned quadrotor helicopter considering actuator dynamics.International Journal of Robust and Nonlinear Control,2017:DOI https://doi.org/10.1002/rnc.3889.

[8]Z.Liu,C.Yuan,Y.Zhang,et al.A learning-based fault tolerant tracking control of an unmanned quadrotor helicopter.Journal of Intelligent&Robotic Systems,2015,84(1/4):145–162.

[9]C.W.Reynolds.Flocks,herds and schools:A distributed behavioral model.ACM SIGGRAPH Computer Graphics,1987,21(4):25–34.

[10]R.Olfati-Saber.Flocking for multi-agent dynamic systems:Algorithms and theory.IEEE Transactions on Automatic Control,2006,51(3):401–420.

[11]F.Cucker,S.Smale.On the mathematics of emergence.Japanese Journal of Mathematics,2007,2(1):197–227.

[12]T.Vicsek,A.Czir´ok,E.Ben-Jacob,et al.Novel type of phase transition in a system of self-driven particles.Physical Review Letters,1995,75(6):1226–1229.

[13]Z.Liu,L.Guo.Connectivity and synchronization of Vicsek model.Science in China Series F:Information Sciences,2008,51(7):848–858.

[14]L.Perea,E.Pedro,G.Gerard.Extension of the Cucker-Smale control law to space flight formations.Journal of Guidance,Control,and Dynamics,2009,32(2):527–537.

[15]F.Cucker,J.G.Dong.Avoiding collisions in flocks.IEEE Transactions on Automatic Control,2010,55(5):1238–1243.

[16]J.Park,H.J.Kim,S.Y.Ha.Cucker-Smale flocking with inter particle bonding forces.IEEE Transactions on Automatic Control,2010,55(11):2617–2623.

[17]S.M.Ahn,H.Choi,S.Y.Ha,et al.On collision-avoiding initial configurations to Cucker-Smale type flocking models.Communications in Mathematical Sciences,2012,10(2):625–643.

[18]R.Olfati-Saber,R.M.Murray.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520–1533.

[19]N.Moshtagh,N.Michael,A.Jadbabaie,et al.Visionbased,distributed control laws for motion coordination of nonholonomic robots.IEEE Transactions on Robotics,2009,25(4):851–860.

[20]O.Saif,F.Isabelle,Z.R.Arturo.Real-time flocking of multiple quadrotor system of systems.IEEE Conference on System of Systems Engineering(SoSE),San Antonio:IEEE,2015:286–291.

[21]A.Belkadi,D.Theilliol,L.Ciarletta,et al.Robust flocking control design for a fleet of autonomous agents.IEEE Conference on Control and Fault-Tolerant Systems(SysTol),Barcelona:IEEE,2016:1–6.

[22]Z.Liu,C.Yuan,Y.Zhang.Active fault-tolerant control of unmanned quadrotor helicopter using linear parameter varying technique.Journal of Intelligent&Robotic Systems,2017,88(2/4):415–436.

[23]Y.Zhang,A.Chamseddine,C.A.Rabbath,et al.Development of advanced FDD and FTC techniques with application to an unmanned quadrotor helicopter testbed.Journal of Franklin Institute,2013,350(9):2396–2422.

[24]Z.Liu,Y.Zhang,X.Yu,et al.Unmanned surface vehicles:An overview of developments and challenges.Annual Reviews in Control,2016,41:71–93.

[25]K.J.Åstr¨om,B.Wittenmark.Computer-Controlled Systems:Theory and Design.Englewood Cliffs:Prentice-Hall,1984.

[26]Y.Zhang,J.Jiang.Integrated design of reconfigurable faulttolerant control systems.Journal of Guidance,Control,and Dynamics,2001,24(1):133–136.

[27]B.Kedjar,A.H.Kamal.DSP-based implementation of an LQR with integral action for a three-phase three-wire shunt active power filter.IEEE Transactions on Industrial Electronics,2009,56(8):2821–2828.