Distributed output feedback stationary consensus of multi-vehicle systems in unknown environments

Vahid REZAEI,Margareta STEFANOVIC

Department of Electrical and Computer Engineering,University of Denver,Denver,CO 80208,U.S.A.

1 Introduction

Control of vehicular systems has received a significant attention among policy makers and researchers during the past two decades due to the increased demand in transportation systems,advances in wireless communication devices,and embedded sensing and computation technologies(see[1,2])such that the market of autonomous vehicular systems will expectedly hit$42B by 2025 and,shortly after that,$85B by 2030[3].

Cooperative analysis and control of multi-vehicle sys-tems have been done from both the systems-theoretic[4,5]and graph-theoretic viewpoints.In the first,the multi-vehicle system is usually considered over a standard string or mesh topology.Along with the advances in wireless and embedded technologies,graph-theoretic tools have created a promising alternative viewpoint in which the behavior of multi-vehicle systems can be analyzed over graphs where nodes represent vehicles and edges indicate inter-vehicle communication.This approach allows to consider more complicated topologies than the standard string or mesh of vehicles[6],and design the multi-vehicle cooperative algorithm independently of the vehicle-level controllers.Reference[7]developed a feedback linearization-like scheme to transform moving robot’s nonlinear dynamics to double integrator model with the goal of cooperative formation;[8]used double integrator models for the formation of unmanned vehicles;single integrators were used in[9]to model multi-robot systems,[6]proposed double integrators to study the relationship between communication topology and the stability of coordination algorithm,and[10]designed vehicle-level controllers for linear models of vehicles and a filtering-based cooperative algorithm for multi-vehicle systems.

Motivated by their wide applications in the cooperation of multi-vehicle and multi-robot systems,significant theoretical research work has been devoted to the distributed control of first-and second-order agents[11–13].Other than multi-agent system of single integrators,it is known that distributed consensus algorithms usually result in a dynamic agreement in which all trajectories evolve during the time.References[14–17]introduced leaderless stationary consensus problem in which agents agree to stop at the same(fixed)position.Nevertheless,multi-vehicle systems are subject to unknown disturbances such as road profile[18,19]or wind[20–22]which may degrade the performance of consensus algorithm or destabilize it.Additionally,proposing a distributed algorithm with fewer absolute measurements than[14–17]may result in a less expensive multi-vehicle system.

Distributed disturbance rejection algorithms have been investigated in the literature of multiagent systems to achieve conventional leaderless or leader-follower agreement among agents.In particular,motivated by the effectiveness of integral action in control systems theory,[23]and[24]studied integral action-based consensus algorithms for multi agent systems of single-and double-integrator agents under persistent disturbances,respectively.In order to consider a wider class of the multiagent systems,[25]showed the disturbance-free algorithms do not achieve conventional consensus in the presence of unknown eventually constant disturbances,and developed an observer-based leader-follower disturbance rejection consensus strategy for linear time in variant dynamical agents.Reference[26]generalized the result to guarantee consensus in the presence of a wider class of unknown disturbances(e.g.,with sinusoidal waveforms).However,because persistent disturbances continuously excite the uncontrollable and unobservable agreement dynamics,these disturbance rejection algorithms are not able to guarantee leaderless stationary consensus in multi-vehicle systems.

Inspired by[26],we develop a dynamic output feedback leaderless stationary consensus algorithm based on the relative output information of vehicles and only a few vehicles’absolute measurements.We propose a framework to transform this dynamic output feedback problem into three low-order subproblems for disturbance rejection,consensus,and observer gain design tasks.Independently of the number of vehicles,consensus and observer gains are systematically found through two robust static state feedback formulations for loworder dynamics subject to fictitious modeling uncertainties.We further prove the proposed framework can be used to guarantee leader-follower stationary consensus in multi-vehicle systems(with a leader whose dynamics are not identical to the follower vehicles),and find analytical solutions for the consensus gains based on the design parameters and inter-vehicle communication graph.We verify the feasibility of proposed leaderless and leader-follower stationary consensus approaches in simulation.

The rest of this paper is organized as follows.In Section 2,we introduce the notation and preliminary concepts.In Section 3,we provide the first contribution of this paper and propose a distributed leaderless stationary consensus algorithm that allows multi-vehicle systems to operate in unknown environments.In Section 4,we further prove the proposed framework for the leaderless scheme can be applied to the leader-follower stationary consensus in multi-vehicle systems.In Section 5,we discuss some challenges that may arise using conventional leaderless stationary algorithms in multivehicle systems,and verify the effectiveness of the proposed approaches through simulation studies.We summarize this paper in Section 6.

2 Notation

In this paper,Rn×ndenotes real-valued n × n matrices,Inidentity matrix with dimension n,0 a matrix of all zeros with appropriate dimension,1nan n×1 vector of all ones,diag{·}a(block)diagonal matrix with elements inside{·}as its diagonal terms,col{xi}a column vector of ordered vectors(or scalars)xifor i∈ {1,2,...,n},and ‖x‖Euclidean norm of the vector x∈Rn.Also,A≻0(≥0)represents positive(semi)definite matrix A,and therow permutation matrix P ∈ Rn×nis an Inwith switched rows.For any symmetric matrix A ∈ Rn×n,there exists a unitary transformation matrix T ∈ Rn×nsuch that T−1AT= Λ is satisfied with Λ ≜ diag{λi}where λi∈ R are eigenvalues of A for i∈{1,2,...,n}[27].Moreover,the Rayleigh-Ritz inequality states λmin(A)‖x‖2≤ xTAx ≤ λmax(A)‖x‖2holds for any symmetric matrix A with λmin(A)and λmax(A)as its minimum and maximum eigenvalues.

In the leaderless scenario,a set V of N nodes is associated to vehicles and the edge set E indicates the inter-vehicle communication topology which is visualized by undirected graph G.This information is abstracted by adjacency matrix A=[aij] ∈ RN×Nin which aij=aji,and aij=1 whenever the i th vehicle receives information from j th vehicle and aij=0 otherwise where i,j∈{1,2,...,N}.This characterization is valid for graphs with no self loop,i.e.,aii=0.The graph Laplacian matrix L ∈ RN×Nis further defined by Lij= −aijforandThe following fact holds for any undirected graphs[28].

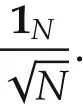
In the leader-follower scenario,we introduce a set of N+1 nodes over graph Glfwhere N vehicles serve as followers and communicate over an undirected graph G,and only a few vehicles receive updates from the leader over aset of directed edges.The information about these leader-to-follower connections is lumped in B=diag{b}where b=col{bi},bi=1 whenever the i th follower receives information from the leader,bi=0 otherwise,and i∈{1,2,...,N}.We partition the leader-follower graph Laplacian matrixas follows:

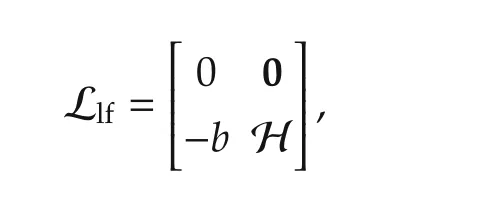
where the first row,with all zeros,implies that the leader does not receive information from followers,and H=L+B ∈ RN×Nwhere L is a graph Laplacian matrix that abstracts the undirected communication topology among followers.Having knowledge about H,it is straightforward to find the leader-to-follower connections B and asymmetric positivedefinite L based on the fact that L 1N=0(see Fact 1).In this sense,we name H a reduced-order Laplacian matrix because it completely characterizes the leader-follower communication graph Glf,and use H(instead of Llf)to develop the ideas of this paper.The following fact holds[29].

Fact 2There duced-order Laplacian matrix Hispositive definite if and only if the leader-follower graph Glfhas a spanning tree with the leader node i=0 as its root.

3 Leaderless stationary consensus

In this section,we develop a systematic framework to design output feedback dynamic stationary consensus algorithm for leaderless multi-vehicle systems.Compared to the existing results in the literature,which are disturbance-free problems with all vehicles’access to their absolute velocity measurements[14–17],the proposed strategy is based on the relative output measurements and a few vehicles’absolute output variables(potentially,only one vehicle),and ensures agreement in the presence of various unknown persistent disturbances.For such a multi-vehicle system with limited information,we first show the relative information-based dynamic consensus task can be reformulated as a set of local stability problems using heterogeneous absolute measurements.Then,in order to have a scalable design for multi-vehicle systems with a high-number of vehicles,we further recast it as three design sub-problems to find disturbance cancellation,robust feedback,and robust observer gains.

3.1 Problem statement

We consider a group of moving vehicles modeled by the following dynamics:

where xi∈R denotes position,vi∈R velocity,ui∈R control input,andrelative output measurement of the i th vehicle.Also,g2∈R are two out putgain scalars which,for g2=0,reduces to the partial measurement scenario for multi-vehicle systems.Whenever i th vehicle has access to its absolute output measurement,we set bi=1 and,otherwise,bi=0.

Fact 3The triple(C,A,B)is controllable and observable where

The effects of unknown environment on the vehicles’dynamics are modeled by a set of heterogeneous persistent disturbances di∈R:

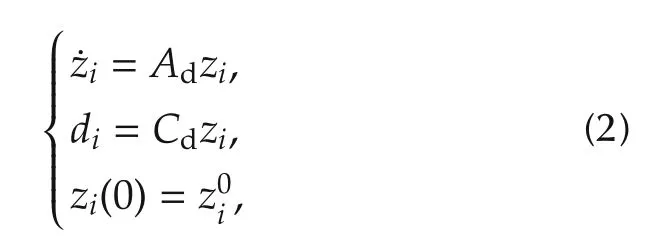
where zi∈Rnzstands for the disturbance-state of the i th vehicle,unknown initial value of the disturbancestate,andand Cd∈ R1×nzare two known constant matrices that determine the shape of disturbance.For this multi-vehicle system,the leaderless stationary consensus task is defined as follows(adopted from[15]):

which should be achieved in the presence of unknown persistent disturbances for all i,j∈{1,2,...,N}.

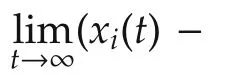
Table 1 Examples of persistent disturbances in(2).

3.2 Main result

In order to guarantee the leaderless stationary consensus of multi-vehicle system(1)in the presence of heterogeneous persistent disturbances(2),we propose a dynamic distributed stationary consensus algorithm:

where αv＞ 0 is a design scalar,and kcx,kcv∈ R and Kcd∈ R1×nzare the control gains to be determined later in this section.The i th vehicle’s estimated positionvelocityand disturbance state variableare found using the distributed observer:

where the observer gains kov,kox∈ R and Kod∈ Rnz×1which will be designed in this section.Also,Nidenotes the neighboring set of the i th vehicle over an undirected graph G which satisfies the following assumption.

Assumption 1The undirected communication graph G is connected(see Fact 1).

We define observer error variablesand find the observer er-ror dynamics based on the relative measurements in vehicles’neighborhoods:

Now,the augmented multi-vehicle system and observer error dynamics are given by

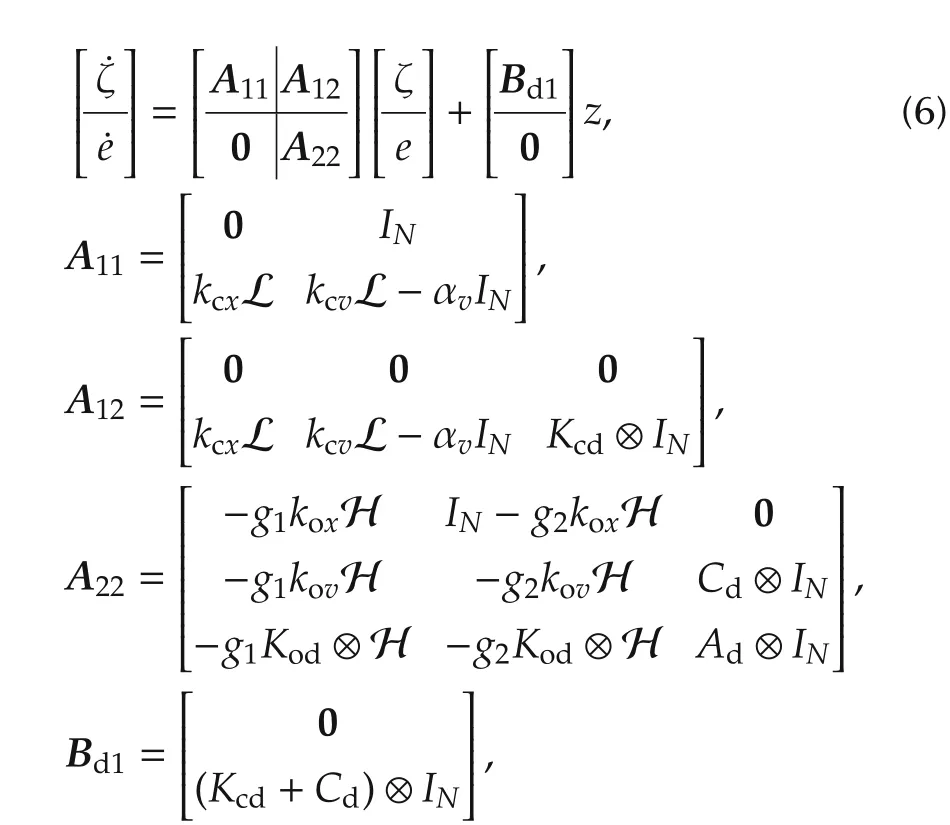
where

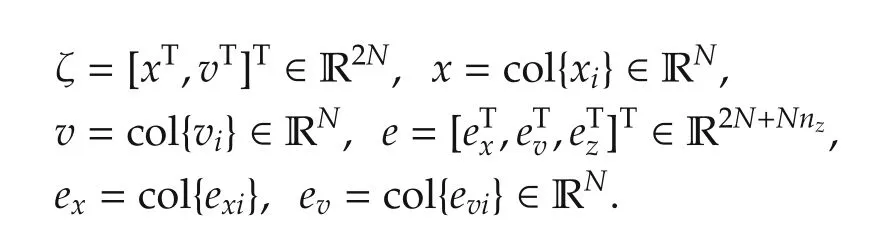
Based on the disturbance generator model(2)and Table 1,it is evident that the dimension nzof disturbance state variable zidepends on the shape of persistent disturbance;thus,wedefine z=col{col{zli},...,col{znzi}}∈RNnzand ez=col{col{ez1i},...,col{eznzi}}∈RNnzwhere

Note that,in the proposed algorithm(4)and(5),depending on g2and bi,only a few vehicles have access to their absolute output measurements.Thus,the closedloop multi-vehicle system cannot be designed following the existing results in the literature of stationary consensus(see[14–17]).On the other hand,we know the definition of adjacency and Laplacian matrices does not admit self loops in the communication graph(see Section 2).Thus,we use the reduced-order(leader-follower)Laplacian matrix H in(6)to analytically handle this situation.

We now take the diagonal blocks in(6)and find two sets of differential equations corresponding to multivehicle and observer error dynamics.In particular,˙e=A22e results in the following transformed aggregated observer dynamics:

in whichandis a unitary transformation matrix that completely diagonalizes the symmetric matrix H aswhere μi＞ 0 are eigenvalues of H≻0 for i∈{1,2,...,N}.We notice that these aggregated error dynamics are composed by N “networked”observer error models:

where μiresult in heterogeneity of the closed-loop networked observers(with kox,kovand Kodin the loop).The word “networked”refers to the effect of inter-vehicle communication topology G on the localized models(7)throughμi.Moreover,using the firstrow˙ζ=A11ζ+Bd1z of(6),the multi-vehicle system is written as follows:

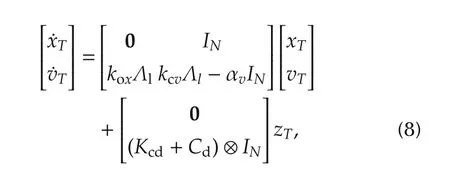
in whichwhereis a unitary transformation that completely diagonalizes the symmetric Laplacian matrix L such thatThe eigenvalue λ1=0 in the diagonal matrix Λldetermines the null space of graph Laplacian matrix L(see Fact 1),and results in a subsystem that does not satisfy the controllability condition.We apply another transformation ξ=Pζ where ζ =[xT,vT]Tand P ∈ R2N×2Nis a row switching matrix that results inandfor i∈ {2,3,...,N}.The subscriptastands for agreement subspace which is uncontrollable,anddindicates controllable disagreement subspace.Using a matrix representation,the transformed system is written as follows:

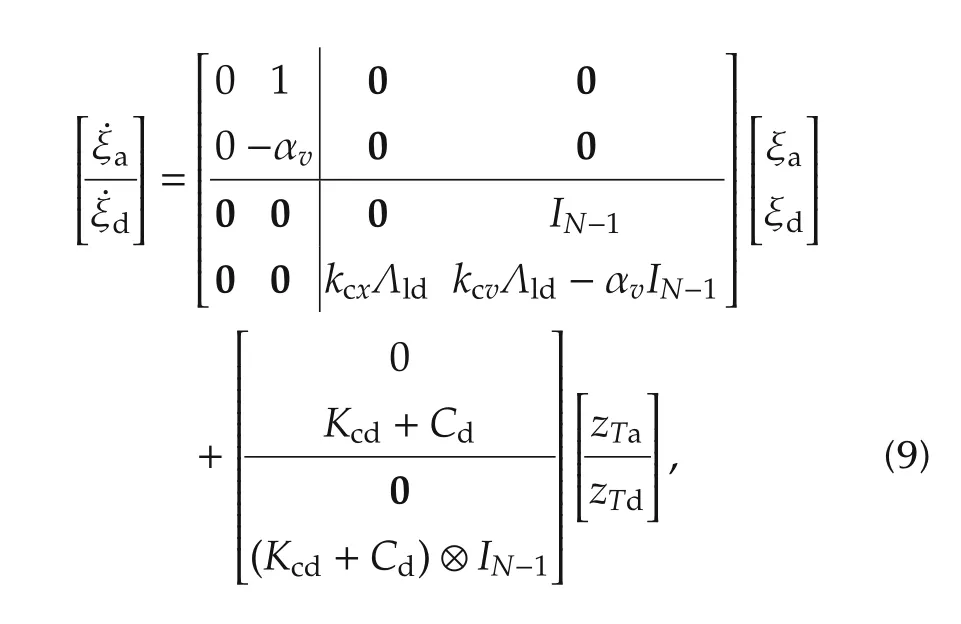
in which the agreement and disagreement dynamics are decoupled from each other.The uncontrollable agreement dynamics show their effects on the stationary consensus value,and will be discussed in Corollary 1 and Lemma 1.However,the controllable disagreement dynamics are made by N−1 heterogeneous networked vehicle models:

for all i∈{2,3,...,N}where the heterogeneity is due to the nonzero eigenvalues λiof L,and the word “networked”is used with the same interpretation as in(7).We now use(7)and(10),and characterize the relative output feedback stationary consensus problem(3)as output feedback stabilization tasks based on the heterogeneously-scaled absolute measurements(due to μiand λi),and establish three conditions for consensus gains to ensure stationary agreement(3)in multi-vehicle system(1)using algorithm(4)and(5).

Proposition 1The dynamic distributed algorithm(4)–(5)guarantees leaderless stationary consensus(3)among vehicles(1)in the presence of persistent disturbances(2)whenever Assumption 1 is satisfied and the following vehicle-level conditions are guaranteed:

1)The disturbance control gain Kcdshould accommodate the effect of unknown heterogeneous disturbances on the networked vehicle dynamics(10).

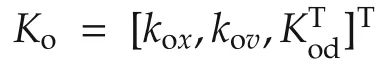
3)For an arbitrarily selected αv＞ 0,the control gain Kc=[kcx,kcv]should stabilize networked vehicle dynamics:

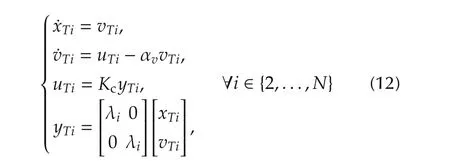
with N−1 heterogeneous measurements where heterogeneity is the effect of positive eigenvalues λiof L.(The effect of αvon the final position of vehicles will be discussed at the end of this section).

The proof of this proposition is immediate based on the aforementioned derivations and noting the fact that,satisfying Part 1 of Proposition 1,separation principle holds for designing observer and controller gains(see the structure of(6)).Although the first part of this proposition is independent of the multi-vehicle system’s dimension,we need to examine the observer gains kox,kovand Kodfor N nonzero eigenvalues μiof H,and control gains kcx,kcvfor N −1 nonzero eigenvalues λiof L.This puts question on the feasibility of using Proposition 1 for multi-vehicle systems with a high-number of vehicles.

In the literature,various viewpoints have been proposed to overcome such a problem.The dominant approaches are based on introducing a scalar correction factor into the consensus algorithm:references[30]and[31]introduced a correction factor to modify the algebraic Riccati equation-based control gain and guarantee leaderless consensus in multiagent systems(e.g.,based on the formulation of this paper,we need to implement ckcx,ckcvin consensus signal(4)where c is a correction gain that should be designed independent of the actual gains kcxand kcv),and[32]used the correction gain to modify its relative measurements(e.g.,in this viewpoint we need to use the modified relative measurements cyriin(4)and(5)with a modification factor c).In the rest of this section,we follow a recent viewpoint on addressing this challenge by reformulating the static output feedback problems(11)and(12)as state-feedback robust control challenge for the nominal networked vehicles’models subject to fictitious uncertainties(e.g.,see[26]and[33]),and provide a systematic approach to find appropriate control and observer gains that guarantee stationary consensus for the multivehicle systems operating in unknown environments.At first,we investigate the control design problem in Parts 1 and 3 of Proposition 1 and,later,we will discuss the observer gain design problem.

Design procedure 1The gains Kcd,kcx,and kcvshould be designed as follows:

1)Disturbance control gain Kcdshould minimize‖(Kcd+Cd)zTi‖where,based on the definition of disturbance generator model(2),Kcd=−Cdaccommodates all persistent disturbances.

2)Robust state feedback gains kcxand kcvshould be designed to stabilize networked robot dynamics:

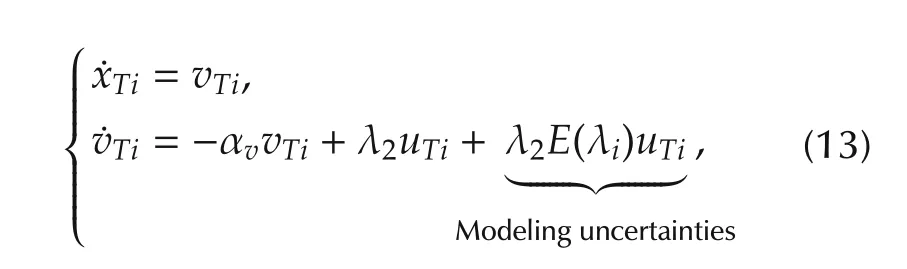
where E(λi)= λi/λ2− 1 ≥ 0 are(communication graph-induced)factitious modeling uncertainties for i∈{2,3,...,N}.

We emphasize that all eigenvalues λimight be known due to the knowledge about communication topology G,but we only use the algebraic connectivity λ2and consider the rest as the sources of modeling uncertainties in order to propose a one-step design procedure and find consensus gains in(4)(compared to the two-step methods in[30–32]).This is the reason to call λ2E(λi)uTi“fictitious”modeling uncertainties.Now,we define a second-order state space model˙ξi=Aξi+BuTifor the nominal networked vehicle dynamics in(13):

and letbe a design matrix and rc＞0 be a design scalar to respectively weigh state and control input variables.In the next theorem,we systematically derive two static consensus gains kcxand kcvthat stabilize uncertain dynamics in Step 2)of Design procedure 1 for all i∈{2,3,...,N}.

Theorem 1Assuming uTi=Kcξihas been found that achieves the minimum of quadratic cost function(15)where UTiis the set of all(admissible)stabilizing signals uTi.Then,Kc=[kcx,kcv]is the required gain to stabilize uncertain networked-vehicle dynamics(13).

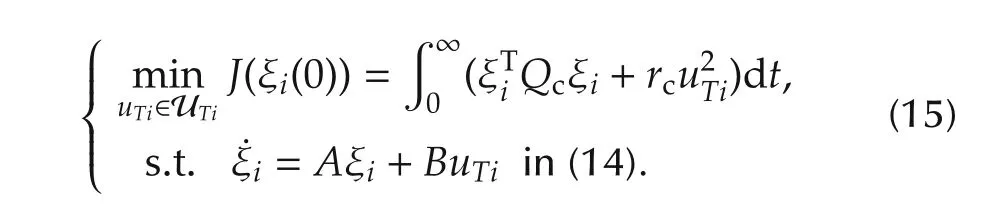
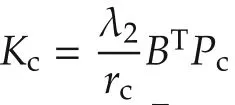
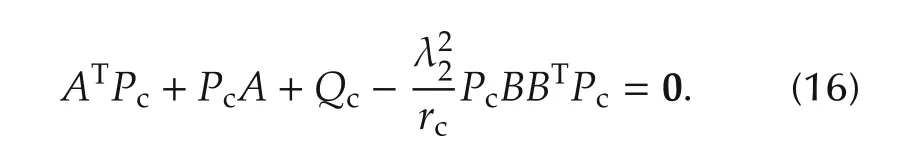
Furthermore,implementing uTi=Kcξi,we know any pairs(ξi,uTi)satisfy two fundamental properties of optimal control theory(e.g.,see Section 3.11 in[34]):

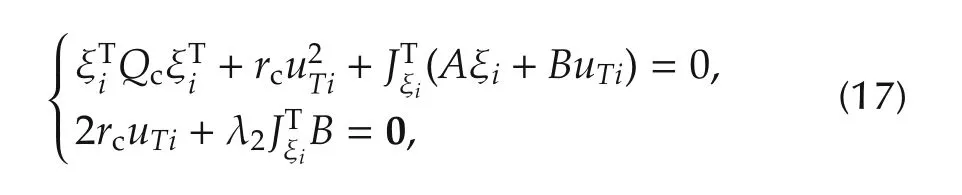
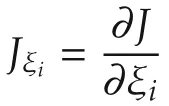
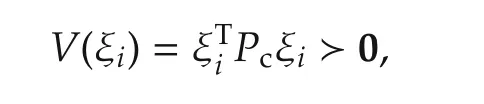
which satisfies V(ξi(0))=J(ξi(0))for any initial conditions,and find its time deviation along the uncertain trajectories in(13):

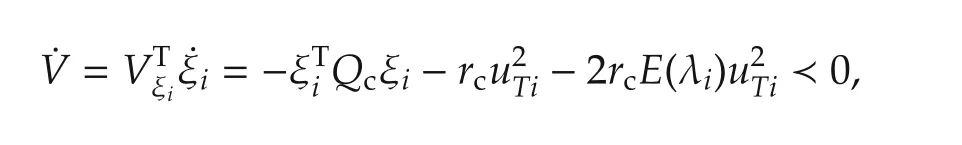
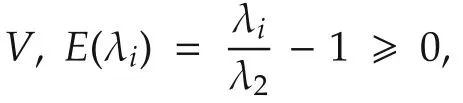
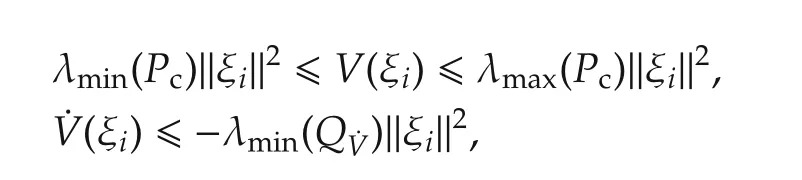
which proves exponential stability of the origin for networked vehicle systems(13)(see Thm.3.6 in[35]).□

Now,we introduce the networked observer’s nominal dynamics:

where Aois defined in(11)andAlso,letbe a design matrix and ro＞0 be a design scalar.In the next theorem,we systematically find the required observer gainto be used in(5).

Theorem 2Findthat achieves the minimum value of(19)subject to completely known dynamical system where Uoidenotes a set of admissible control signals for uoi.Then,Kois the required observer gains for dynamical system(11)in Step 2)of Proposition1.

ProofA sketch of this poof can be given by noticing that the dynamical system in(19)is dual to(18).We can similarly find the dual representation for(11).Then,this theorem is proved following the steps in the proof of Theorem 1 for the dual problem and based on ARE:

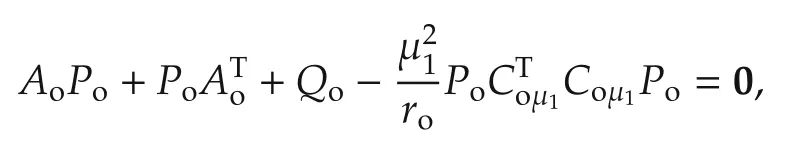
where the unique stabilizingexists by verifying observability and controllability offor□

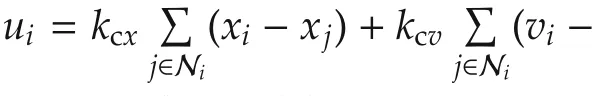
Corollary 1Assuming perfect state and disturbance measurements,the observer-free consensus algorithm(4)will result in the following stationary agreement values:

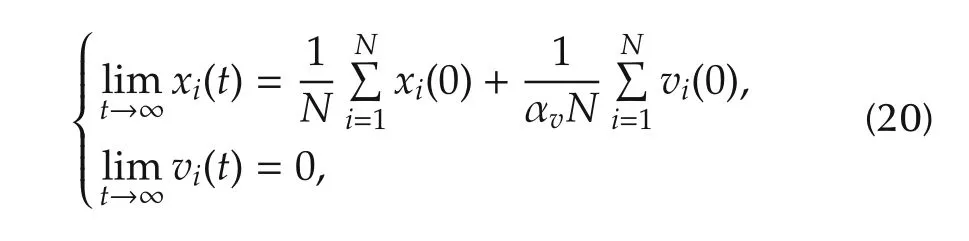
ProofBased on(9),we know agreement dynamics are decoupled from the disagreement dynamics(respectively determined by ξaand ξd).The agreement dynamics are modeled byandand we write the solution of these differential equations asandwhich result in the following limit behavior:

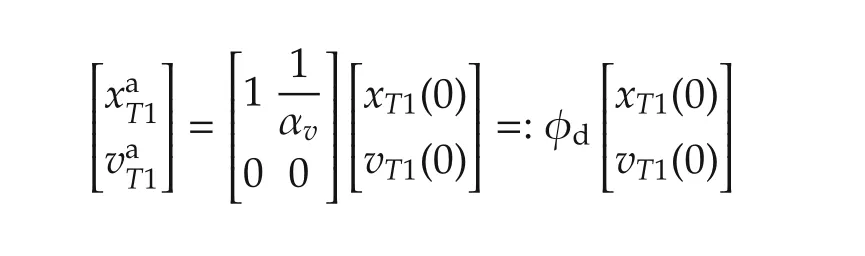
because αv＞ 0 andas(this αvis a design scalar and can be tuned to achieve desirable consensus behavior).Note that the superscriptadenotes the“agreement”value as.Letwheretion such that(see Fact 1).If we rewrite this result based on the agreement and disagreement variables and useis the diagonalizing unitary trans for ma-(based on Theorem 1),we find

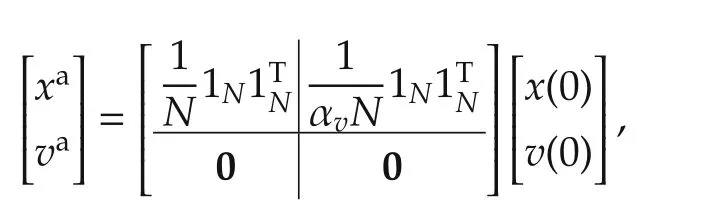
in which

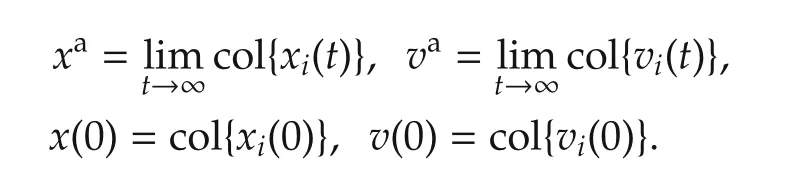
Lemma 1The observer-based output feedback stationary consensus algorithm(4)and(5)results in an agreement on the following point in the presence of unknown persistent disturbances:

ProofWe begin from the augmented multi-vehicle and observer error dynamics(6),substitute Kcdby−Cd,and find

in which

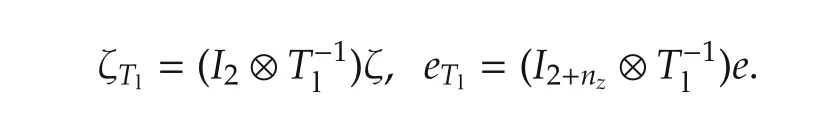
Based on a row switching transformation Pl=diag{P,whereis defined in(9),we write the disagreement dynamics as follows:

The solution of second equation iswhere,as∞,the integral converges to a constant βI∈ R(because the error variables go to zero).Thus,αv＞ 0 results in

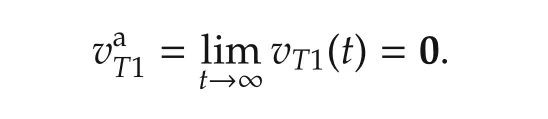
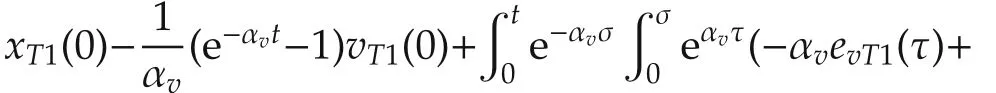
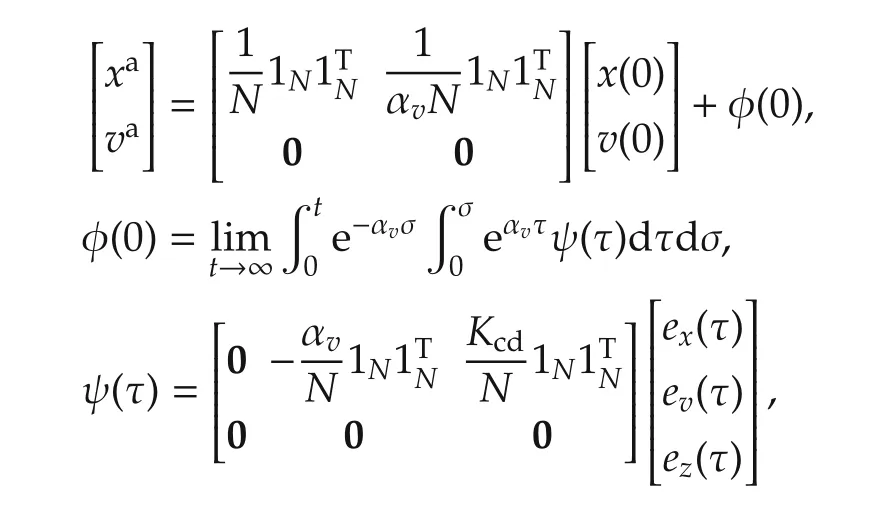
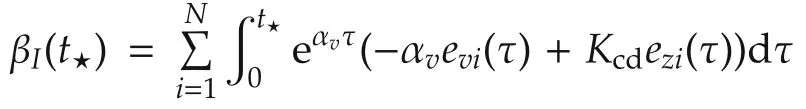
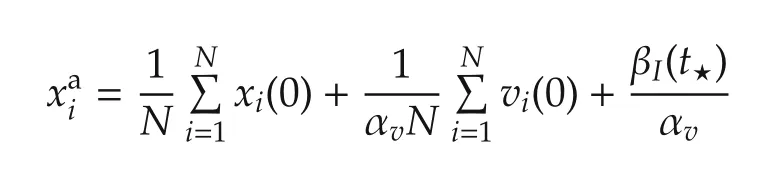
is also a constant value. □

In summary,based on the formulation(12)(also(13)),Theorem 1 guarantees the stability of disagreement dynamics in(9)is achieved for any “arbitrarily”selected αv＞ 0,and Lemma 1 shows this αvadds a level of flexibility to tune the internal behavior of multi-vehicles’agreement dynamics(although they remain“cooperatively”uncontrollable according to the partitioning in(9)).Additionally,as expected,the last term inindicates that agreement value depends on the average of velocity and disturbance state estimation errors’transient behavior.This will be discussed in the simulations of Section 5.

4 Leader-follower stationary consensus

In Section 3,we have developed an output feedback leaderless stationary consensus algorithm for multivehicle systems modeled by double integrators in which,unlike[14–17],only a few vehicles have access to their absolute output measurements and all of them are subject to unknown persistent disturbances.Now,we adopt the result of Section 3 and develop a systematic approach to design a leader-follower stationary algorithm.In particular,we find the closed-form solution for consensus gains purely based on the design matrices and smallest positive eigenvalue of the reduced-order Laplacian matrix corresponding to the leader-follower communication graph.

4.1 Problem statement

In this section,we consider a multi-vehicle system where the followers are modeled by second-order dynamics:

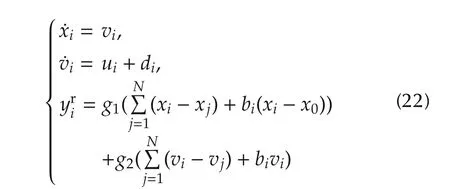
for i∈{1,2,...,N},bi=1 whenever the i th vehicle is aware of its relative distance to the reference position and potentially is aware of its absolute velocity(depending on g2),and bi=0 otherwise.All variablesare defined similar to the leaderless consensus problem in Section 3,and we emphasize that g1≠0.The reference point is commanded by a stationary leader:

which,unlike followers,is described by a first-order model and its adjustable initial state value x0(t)=x0(0)denotes the desired position.Now,we define the leader follower stationary consensus as follows:

where t0≥0 denotes the time of change in the reference command.Before proposing the main result of this section,we make an assumption on the leader-follower communication graph topology Glf.

Assumption 2The leader-follower graph Glfhas a spanning tree with the leader node i=0 as the root(see Fact 2).

4.2 Main result

In this section,we propose a dynamic distributed leader-follower stationary consensus algorithm in order to ensure agreement(24)in multi-vehicle systems(22)and(23):

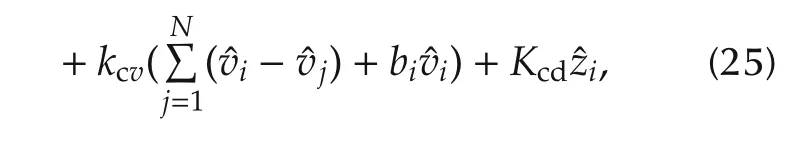
whererespectively denote position and velocity,andrepresents the disturbance state of the i th vehicle estimated by the following distributed observer:

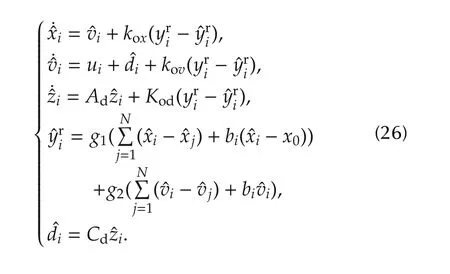
We define observer error variablesand find observer error dynamics

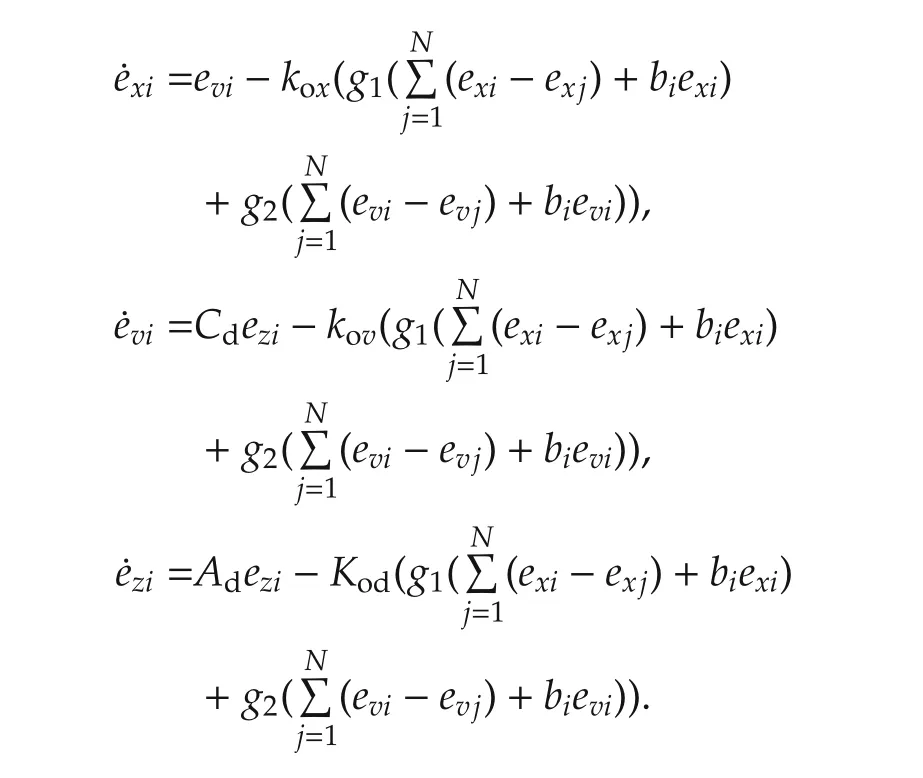
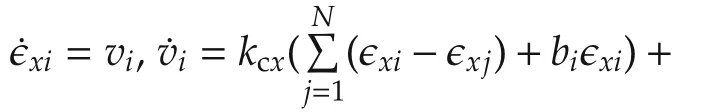
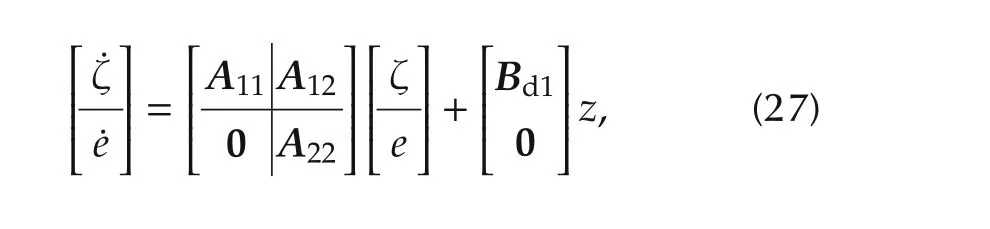
where

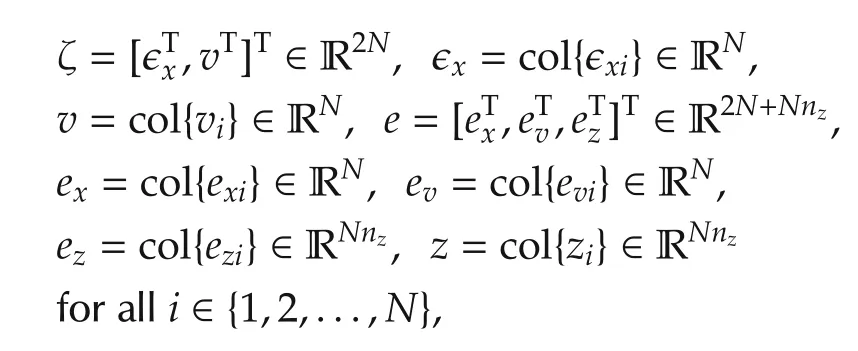
and the sub-matrices are as follows:

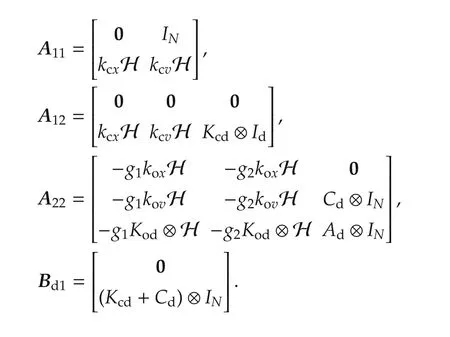
Based on the augmented system(27),we conclude the separation principle holds,and consensus and observer gains can be designed independent of each other.For the observer design purpose,we find the following networked observer dynamics:

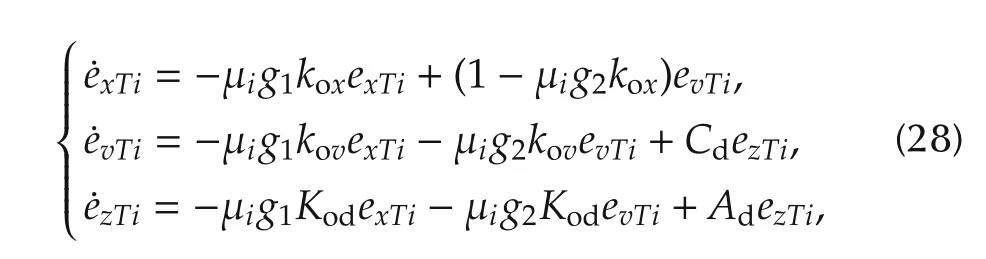
which shows the proposed leader-follower stationary consensus algorithm(25)and(26)has resulted in the same problem as the leaderless consensus scenario in(11).For the control gain design problem,since H is a symmetric positive-definite matrix,we find a completely controllable diagonal representation:

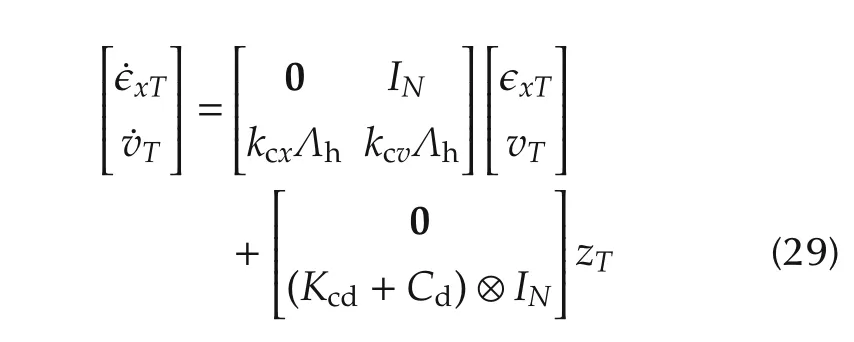
based onandwhereis defined such thatdiag{μi}for i∈ {1,2,...,N}.The transformed dynamics(29)are in fact composed by N heterogeneous networked leader-follower tracking error systems:

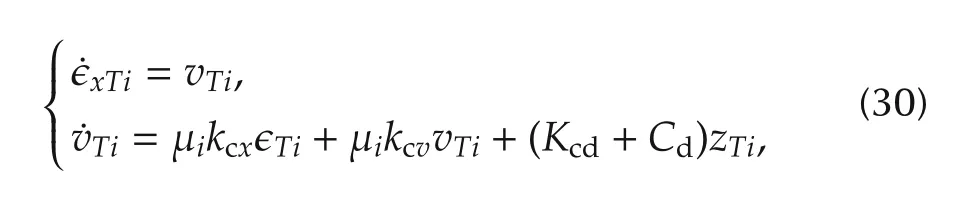
in which μi＞ 0 for all i∈ {1,2,...,N}.Therefore,the following proposition holds in this section.

Proposition 2Suppose Assumption 2 is satisfied by the communication graph Glf.The dynamic distributed algorithm(25)–(26)ensures leader-follower stationary agreement(24)in multi-vehiclesy stems(22)in the presence of unknown disturbances(2)whenever,in addition to Steps 1 and 2 of Proposition 1,the control gain Kc=[kcxkcv]stabilizes the networked leader-follower tracking error dynamics:

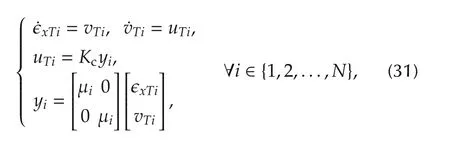
whereμi＞ 0are the eigenvalues of reduced-order Laplacian matrix H for all i∈{1,2,...,N}.

This proposition,along with the observer dynamics(28)and disturbance component in(30),shows the distributed stationary leader-follower algorithm(25)–(26)is formulated such that the disturbance control gain can be found following Step 1)in Design procedure 1,and the observer gain can be designed using Theorem 2 in Section 3.In the next design procedure,we propose a systematic framework to find the consensus gains kcxand kcvbased on a robust control formulation for modified networked leader-follower tracking error dynamics with a homogeneous nominal part and heterogeneous fictitious modeling uncertainties.

Design procedure 2Design state feedback gains kcx,kcv∈R that stabilize the networked vehicle dynamics with homogeneous nominal model and heterogeneous fictitious modeling uncertainties:

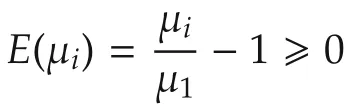
Note that we originally proposed a dynamic output feedback stationary consensus algorithm(25)and(26)using relative measurements;converted it to three subproblems to design consensus,observer,and disturbance gains in Proposition 2 where the consensus gains kcxand kcvwere the stabilizing solutions for N static“output feedback”networked vehicles using N scaled absolute measurements;and,eventually,reformulated the problem as N static“state feedback”robust stabilization tasks using vehicles’absolute state measurements(Design procedure 2).Now,we introduce a secondorder state space realization˙ξi=Aξi+BuTiwhich models the nominal dynamics of(32):

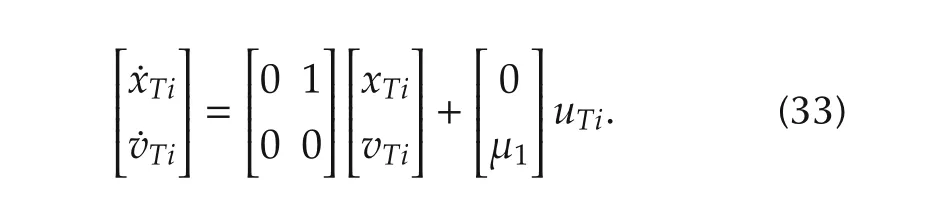
Furthermore,we defineas the state weighting,and rc＞0 as the control input weighting design matrices.In the next theorem,we propose a systematic framework to find the required consensus gains as a single robust state feedback problem.

Theorem 3The solution uTi=Kcξito the minimization problem(34),where UTidenotes the set of all stabilizing state feedback controllers uTi,stabilizes the heterogeneous networked vehicle dynamics(32)for all i∈{1,2,...,N}.

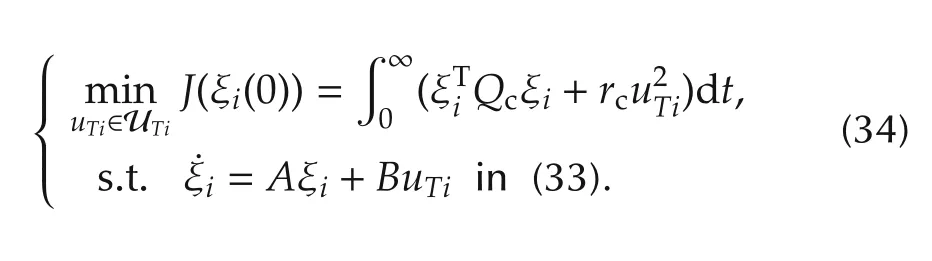
ProofWe mention that,although system matrices(A,B)in(34)is different from(15),the minimization problems are structurally the same such that the fundamental properties(17)are still valid for any pairs ξi,uTiof this leader-follower control theorem.Therefore,a detailed proof can be found by following the steps of proof in Theorem 1.This is omitted for brevity. □

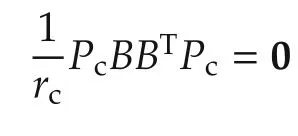
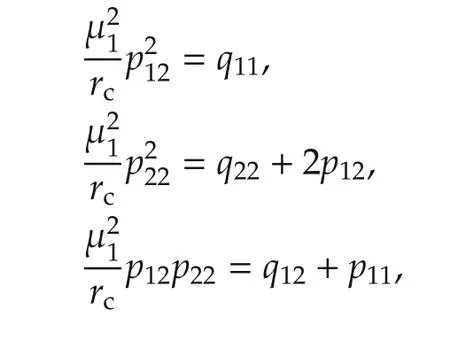
which result in a unique positive-definite stabilizing solution:

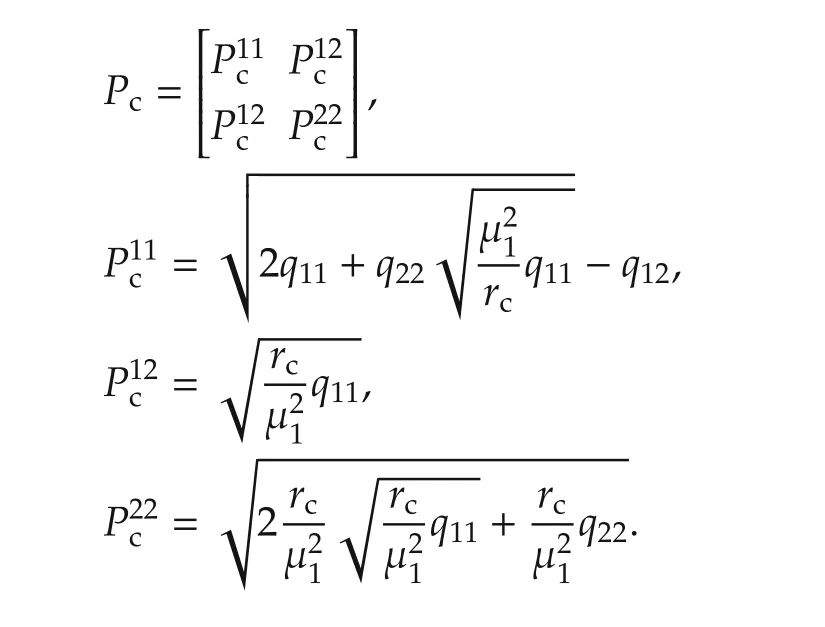
Consequently,we find closed-form solutions for the consensus gains kcxand kcvexplicitly based on the design matrix Qc,scalar rc,and smallest eigenvalue of reduced-order Laplacian matrix μ1of H:

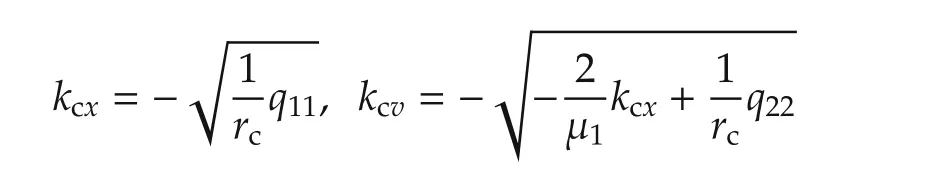
using the optimal gain formula

We note that Pc(1,1)＞0 is guaranteed based on the observability and stabilizability ofA,B).As is seen,the position consensus gain kcxis not directly affected by the communication network G(or μ1);however,a network-dependent fraction of it appears in the velocity consensus gain kcv(i.e.,seethat is added toThese closed-form solutions can be used in tuning of the weighting matrices Qcand rc,and also for the communication topology design purpose.We mention that the tuning process can be further simplified by letting q12=q21=0 or using Qc=qcI2for a scalar tuning parameter qc＞0.

5 Simulation verification

In this section,we set up leaderless and leader follower case studies to be used in the simulation verifications,review some major challenges in conventional(non-stationary)leaderless consensus problem through simulation,verify the feasibility of proposed stationary leaderless algorithm of Section 3 and leader-follower approach of Section 4.

5.1 Problem setup

In the leaderless problem,we consider a group of five vehicles modeled by(1)with g1=1 and g2=0,and assume nodes 1 and 2 have access to their absolute position information(i.e.,b1=b2=1).Vehicles are at initial conditions x1(0)=[−10,20]T,x2(0)=[15,−15]T,x3(0)=[10,15]T,x4(0)=[−30,20]T,and x5(0)=[20,−30]T(which are unknown to the designer).Moreover,vehicles are subject to heterogeneous constant disturbances d1=2,d2=5,d3=3,d4=9 and d5=4.We let vehicles to exchange information over the leaderless graph in Fig.1.

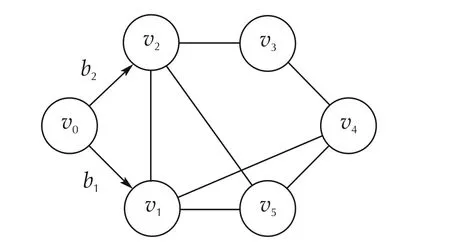
Fig.1 Leaderless communication:By removing node v0 and edges originating from it,nodes v1–v5 and the associated edges represent an undirected leaderless communication topology G with graph Laplacian matrix L.We assume agents v1 and v2 have access to their absolute measurements.Leader-Follower communication:Agents v1–v5 communicate over undirected graph G,nodes v1 and v2 are aware of their relative distance to the leader vehicle v0 such that the entire multi-vehicle system v0–v5 builds a leader-follower communication graph G lf with a reduced-order Laplacian matrix H=L+B where B=diag{1,1,0,0,0}.

In the leader-follower scenario,we add a leader agent v0modeled by(23)where its initial value can be commanded globally(and we will use a square wave input in simulation),and let vehicles to communicate over Glfin Fig.1.Moreover,vehicles are subject to sinusoidal disturbances:d1=7sin(0.5t),d2=5.5sin(0.5t),d3=6sin(0.5t),d4=2sin(0.5t),and d5=4sin(0.5t).

5.2 Overview of the literature

We overview the problems that may arise using the existing conventional leaderless consensus algorithms with disturbance rejection capability.In particular,we first upgrade the leaderless consensus algorithm of[26]to be able to include unstable vehicle dynamics,and find the following agreement and final values using an observer-based approach over the leaderless graph G of Fig.1:

where we assume all observers are at initial rest condition exceptˆx3(0)=[10,−15]T,and vehicles are subject to unknown constant disturbances(see Section 5.1).A simulation result is depicted in Fig.2 which verifies all vehicles reach to the(upgraded)agreement values in(35).

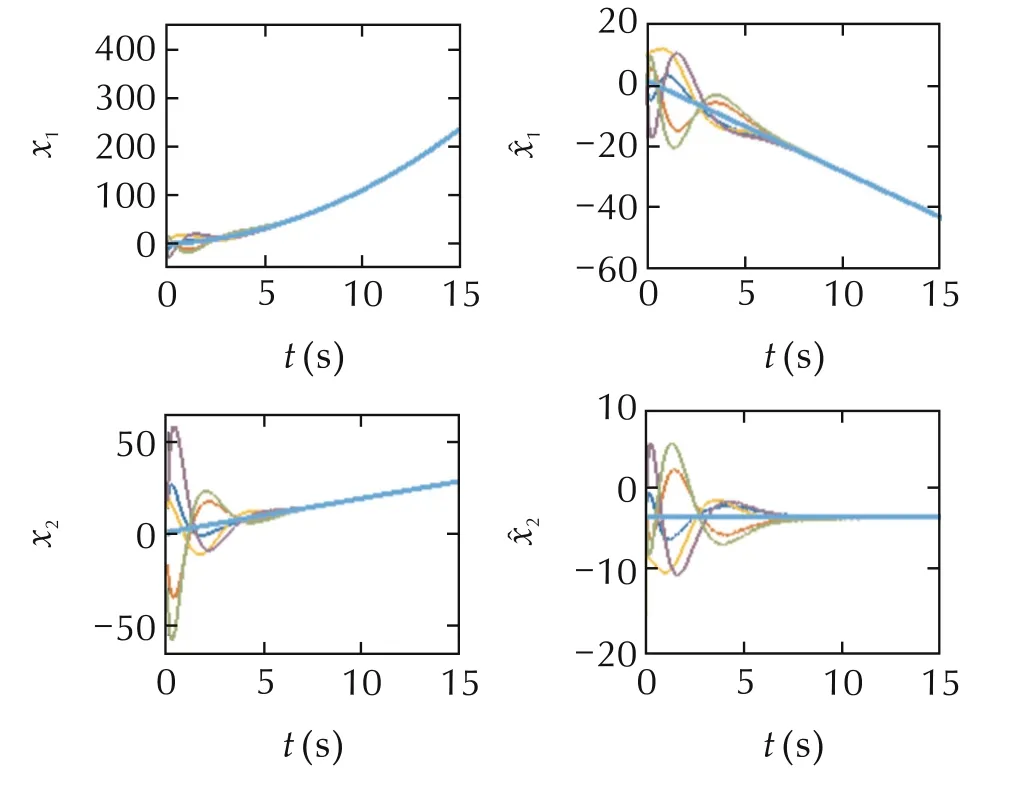
Fig.2 Simulation results using an upgraded leaderless consensus algorithm of[26](to include unstable systems)subject to unknown constant disturbances.All observers are at initial rest conditions exceptˆx3(0).As is seen,all position and velocity variables,and their estimations are unbounded.However,the estimations differ from the actual variables due to the nullity in observer dynamics.

However,we notice a practically undesirable collective behavior where vehicles continuously increase their speed because of the nullity in system and disturbance state estimations(which also results in a mismatch between the actual variables and their estimations).In the next simulation,we assume all observers are at initial rest conditions and find that,independent of vehicles’initial conditionsfor all i∈{1,2,...,5}.As is depicted in Fig.3,although the observer variables remain bounded,the nullity(unobservability)of leaderless consensus is still problematic in the presence of persistent disturbances,and results in an uncontrolled increase in vehicles’speed.

Fig.3 Simulation results for an upgraded leaderless consensus algorithm of[26]under the same scenario as Fig.2 except,now,all observers are at initial rest conditions.As is shown,although estimation variables converge to zero,the vehicles’consensus behavior remains the same as Fig.2.

We further modify the leader-follower result of[26]to beableto in cludeun stable agent dynamics and,in Fig.4,show that all vehicles v1–v5agree on the “second-order”leader’s velocity and follow its position with constant speed.

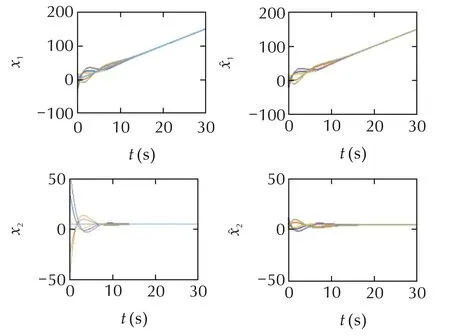
Fig.4 Simulation results using an upgraded leader-follower consensus algorithm[26](to include unstable systems)subject to unknown constant disturbances as in Figs.2 and 3.

5.3 Leaderless stationary consensus

In this section,we verify the feasibility of the proposed observer-based leaderless stationary consensus algorithm in Section 3.We show that the proposed strategy overcomes the undesirable increasing speed problem of the conventional leaderless algorithm in Section 5.2.The multi-vehicle system is implemented under the same scenario as in Section 5.1 over the leaderless graph of Fig.1.

At first,in Fig.5,we consider an observer-free algorithm and verify that vehicles velocity reach to zero and they agree on the positionas expected by Corollary 1.In Fig.6,we use the proposed observer-based algorithm(4)and(5)where all observers are at initial rest condition,and show all vehicles reach to a“stationary”agreement on their position at.Moreover,unlike the conventional leaderless scenario of Fig.3,estimations are the same as actual position and velocity variables of vehicles.We further note that the difference in agreement position values of Figs.5 and 6 is expected based on Lemma 1.

Fig.5 Observer-free leader less stationary consensus algorithm based on Corollary 1 in the presence of constant disturbances.All vehicles agree on a fixed position

Fig.6 Leaderless stationary consensus algorithm of Section 3 where all observers are at initial rest condition and the agreement is on.The dashed line show the agreement value of Fig.5(see Lemma 1).

In Fig.7,we initialize the second observer at[−10,15,0]Tand show the effect of observer error(trajectories)on the consensus value where,unlike Fig.6,the agreement is on.Finally,based on Theorem 2,we redesign observer gains by setting the state weighting matrix to be 103greater than the first design(see Fig.6),and find a new agreement onwhich is shown in Fig.8.In all of these simulation scenarios,disturbances are estimated precisely as is depicted in Fig.9.

Fig.7 Leaderless stationary consensus algorithm with all observers are at initial rest condition except.Different from Fig.6,the agreement is on.This shows the effect of observer error trajectories on agreement values(see Lemma1).

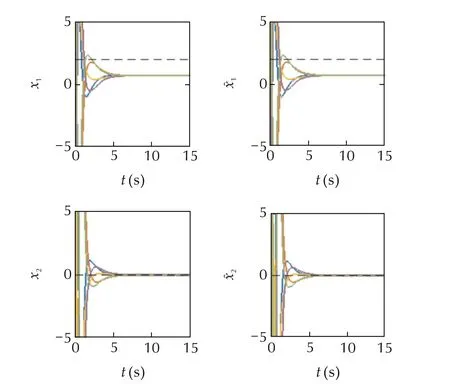
Fig.8 Leaderless stationary consensus under the same configuration as Fig.6 with a new set of design matrices.The agreement is on.This verifies the effect of observer dynamics(error trajectories)on the stationary agreement value.

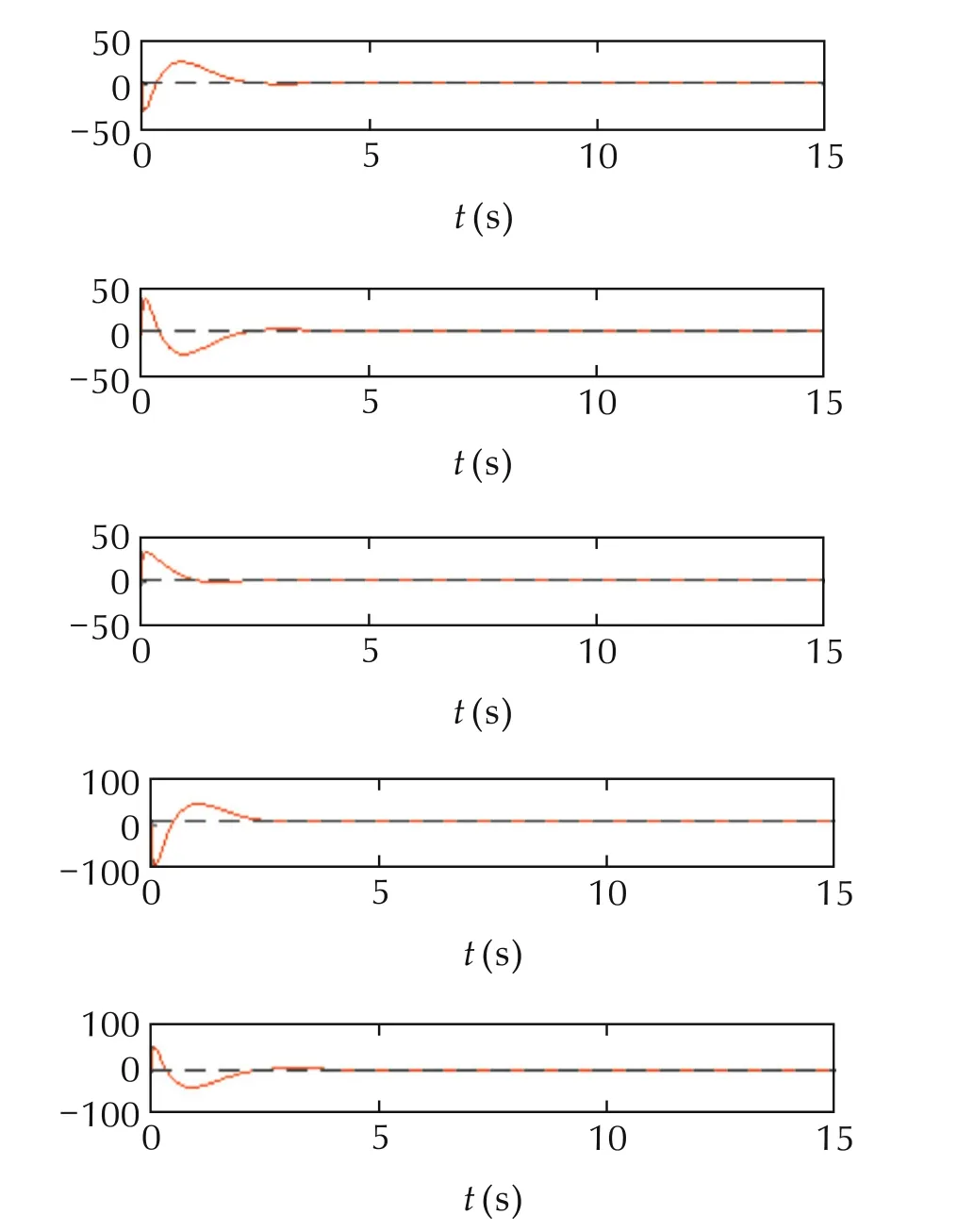
Fig.9 In all leader less stationary consensus simulations,disturbances are estimated precisely(with differences in the transient behavior).Top to bottom:w1 to w5(black)and their estimations(red).

5.4 Leader-follower stationary consensus

In this section,we investigate the effectiveness of leader-follower stationary algorithm(25)and(26)in ensuring a stationary consensus on a adjustable position with limited information about the leader(as discussed in Section 4).We consider a leader-follower setup subject to sinusoidal disturbances,as introduced in Section5.1.For this setup,we use a square wave to command the desired position of vehicles.Although only two vehicles are aware of their relative distances to the desired reference point,Figs.10 and 11 show all vehicles precisely estimate their positions,velocities,and disturbances;and agree on the commanded stationary point.

Fig.10 Leader-follower stationary consensus:State variables and their estimations.The dashed back waves represent the leader’s command.

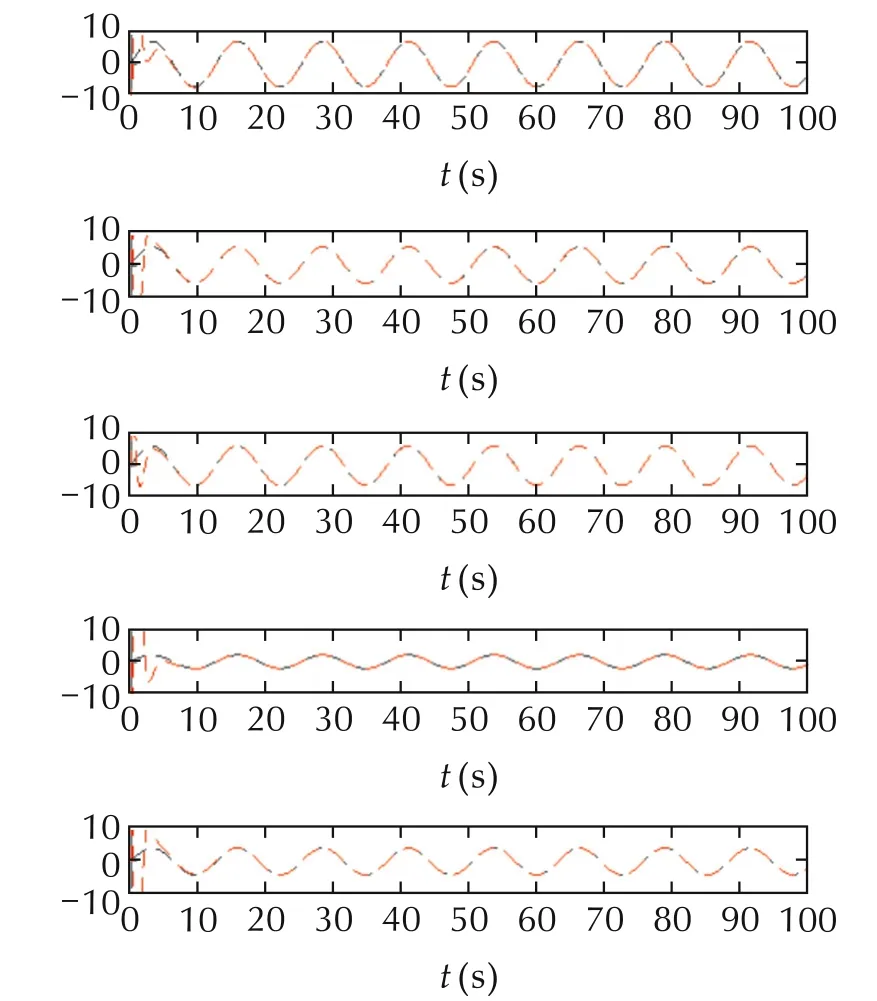
Fig.11 Leader-follower stationary consensus.Top to bottom are w1 to w5(black)and their estimations(red).

6 Summary

We design leaderless and leader-follower stationary consensus algorithms which ensure all vehicles’agreement on a fixed point in the presence of unknown persistent disturbances with only a few vehicles’absolute measurements.In both leaderless and leader follower scenarios,we provide a systematic framework that transform the high-order dynamic relative-output feedback stationary consensus challenge to three loworder subproblems to be used in designing disturbance,consensus,and observer gains.We formulate the consensus and observer gain design tasks as two robust static feedback problems for modified vehicle dynamic subject to fictitious modeling uncertainties which are induced by communication graph topology.In simulation,we discuss the challenges of applying non-stationary disturbance rejection algorithms to multi-vehicle systems,and verify the feasibility of using proposed strategies for multi-vehicle systems in unknown environments where vehicles might be subject to road profile and wind disturbances.

[1]D.Cruz,J.McClintock,B.Perteet,et al.Decentralized cooperative control.IEEE Control Systems Magazine,2007,27(3):58–78.

[2]L.Bento,R.Parafita,U.Nunes.Inter-vehicle sensor fusion for accurate vehicle localization supported by V2V and V2I communications.International Conference on Intelligent Transportation Systems,Anchorage:IEEE,2012:907–914.

[3]R.Langari.Autonomous vehicles:a tutorial on research and development issues.American Control Conference,Seattle:IEEE,2017:4018–4022.

[4]P.Seiler,A.Pant,J.Hedrick.Disturbance propagation in vehicle strings.IEEE Transactions on Automatic Control,2004,49(10):1835–1842.

[5]Y.Zhao,P.Minero,V.Gupta.On disturbance propagation in leader-follower systems with limited leader information.Automatica,2014,50(2):591–598.

[6]W.Ren,E.Atkins.Distributed multi-vehicle coordinated control via local information exchange.International Journal of Robust and Nonlinear Control,2007,17(10/11):1002–1033.

[7]J.Lawton,R.Beard,B.Young.A decentralized approach to formation maneuvers.IEEE Transactions on Robotics and Automation,2003,19(6):933–941.

[8]R.Xue,G.Cai.Formation flight control of multi-UAV system with communication constraints.Journal of Aerospace Technology Management,2016,8(2):203–210.

[9]A.Jadbabaie,J.Lin,S.Morse.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):988–1001.

[10]T.Yucelen,E.Johnson.Control of multi-vehicle systems in the presence of uncertain dynamics.International Journal of Control,2013,86(9):1540–1553.

[11]W.Ren,R.Beard,E.Atkins.A survey of consensus problems in multi-agent coordination.American Control Conference,Portland:IEEE,2005:1859–1864.

[12]W.Yu,G.Chen,C.Ming.Some necessary and sufficient conditions for second-order consensus in multi-agent systems.Automatica,2010,46(6):1089–1095.

[13]N.Huang,Z.Duan,G.Chen.Some necessary and sufficient conditions for consensus of second-order multi-agent systems with sampled position data.Automatica,2016,63:148–155.

[14]C.-L.Liu,F.Liu.Stationary consensus of heterogeneous multiagent systems with bounded communication delays.Automatica,2011,47(9):2130–2133.

[15]J.Qin,C.Yu,S.Hirche.Stationary consensus of asynchronous discrete-time second-order multi-agent systems under switching topology.IEEE Transactions on Industrial Informatics,2012,8(4):986–994.

[16]Y.Feng,S.Xu,F.Lewis,B.Zhang.Consensus of heterogeneous first-and second-order multi-agent systems with directed communication topologies.International Journal of Robust and Nonlinear Control,2015,25(3):362–375.

[17]Y.Pei,J.Sun.Necessary and sufficient conditions of stationary average consensus for second-order multi-agent systems.International Journal of Systems Science,2016,47(15):3631–3636.

[18]C.Gohrle,A.Schindler,A.Wagner,et al.Road profile estimation and preview control for low-bandwidth active suspension systems.IEEE/ASME Transactions on Mechatronics,2015,20(5):2299–2310.

[19]I.Youn,M.Khan,N.Uddin,et al.Road disturbance estimation for the optimal preview control of an active suspension system based on tracked vehicle model.International Journal of Automotive Technology,2017,18(2):307–316.

[20]A.Cho,S.Kim,C.Kee.Wind estimation and airspeed calibration using a UAV with a single-antenna GPS receiver and pitot tube.IEEE Transactions on Aerospace and Electronic Systems,2011,47(1):109–117.

[21]B.Arain,F.Kendoul.Real-time wind speed estimation and compensation for improved flight.IEEE Trans actions on Aerospace and Electronic Systems,2014,50(2):1599–1606.

[22]H.Shen,N.Li,H.Griffiths,et al.Tracking control of a small unmanned air vehicle with airflow awareness.American Control Conference,Seattle:IEEE,2017:4153–4158.

[23]T.Yucelen,M.Egerstedt.Control of multiagent systems under persistent disturbance.American Control Conference,Montreal:IEEE,2012:5264–5269.

[24]M.Anderson,D.Dimarogonas,H.Sand berg,et al.Distributed control of networked dynamical systems:static feedback integral action and consensus.IEEE Transactions on Automatic Control,2014,59(7):1750–1764.

[25]W.Cao,W.Zhang,W.Ren.Leader-follower consensus of linear multi-agent systems with unknown external disturbance.Systems&Control Letters,2015,82:64–70.

[26]V.Rezaei,M.Stefanovic.Distributed leaderless and leader follower consensus of linear multiagent systems under persistent disturbances.Mediterranean Conference on Control and Automation,Athens,Greece:IEEE,2016:386–391.

[27]R.Horn,C.Johnson,Matrix Analysis.Cambridge:Cambridge University Press,2013.

[28]M.Mesbahi,M.Egerstedt.Graph Theoretic Methods in Multiagent Networks.Princeton:Princeton University Press,2010.

[29]W.Ni,D.Cheng.Leader-following consensus of multi-agent systems under fixed and switching topologies.Systems&Control Letters,2010,59(3/4):209–217.

[30]S.-E.Tuna.LQR-based coupling gain for synchronization of linear systems.arXiv,2008:arXiv:0801.3390.

[31]H.Zhang,F.Lewis,A.Das.Optimal design for synchronization of cooperative systems:state feedback,observer and output feedback.IEEE Transactions on Automatic Control,2011,56(8):1948–1952.

[32]Z.Li,Z.Duan,G.Chen,et al.Consensus of multiagent systems and synchronization of complex networks:a unified viewpoint.IEEE Transactions on Circuits and Systems I:Regular Papers,2010,57(1):213–224.

[33]V.Rezaei,M.Stefanovic.Distributed decoupling of partially unknown interconnected linear multiagent systems:state and output feedback approaches.IFAC-PapersOnLine,2017,50(1):1766–1771.

[34]D.Kirk.Optimal Control Theory:An Introduction.Englewood Cliffs:Prentice Hall,1970.

[35]H.Khalil.Nonlinear Control.Englewood Cliffs:Prentice Hall,2014.