Consensus controller for multi-UAV navigation

Patrik KOLARIC ,Ci CHEN ,Ankur DALAL,Frank L.LEWIS,3

1.UTA Research Institute,University of Texas at Arlington,7300 Jack Newell Blvd S,Fort Worth,TX,76118,U.S.A.;

2.School of Automation,Guangdong University of Technology;Guangdong Key Laboratory of IoT Information Technology,Guangzhou Guangzhou 510006,China

3.State Key Laboratory of Synthetical Automation for Process Industries,Northeastern University,Shenyang Liaoning 110819,China

1 Introduction

Cooperative control of multiple unmanned aerial vehicles(UAVs)that share a global task has recently drawn a lot of attention.The last decades have witnessed a rapid development of micro UAVs and the idea of multiagent UAV systems performing tasks grew with it.This is due to the fact that a group of simple individual vehicles may facilitate the execution of a complex task with higher robustness to potential technical faults.Moreover,multi-agent systems also have an economical and logistical advantage,simply because the failure of a single agent does not put the whole mission into jeopardy.That makes a single agent in the system expendable and its design requirements less rigorous.Those advantages are widely recognized in research literature[1–3].

We are interested in the consensus control of multiple UAVs,especially quad copters.It is shown in[4]that a two-loop nonlinear scheme using input-output linear is ation technique can be employed to satisfy the tracking performance.Moreover,a neural network based back stepping design for UAV is provided in[5],where an inverse kinematics solution is applied akin to that in the manipulator control such as[6].Nonlinear models of UAV and linearization procedure is covered in[7,8].New control techniques have been proposed to allow multiple vehicles to work cooperatively(see[9–14]).Specific problem of UAV formation control in terms of position and attitude was addressed in[15–17].Finally,more intricate nonlinear approach to control design for multi-agent system was covered in[18,19].

More recently,further work is considered to quantify the performances of the whole multi-UAV system and the local UAV.Its formulation falls into a category of cooperative optimal control and game theory.In particular,reference[20]uses linear quadratic regulator based optimal control to achieve the synchronization of linear systems.Non-zero-sum games are studied for multiple players in[21–23],where the adaptive algorithm learns online the solution of coupled Riccati equations and coupled Hamilton-Jacobi equations.Even though good results were obtained,little research has been carried out to handle the measurement noise imposed on each local UAV.

Note that when the noise is injected into the measurement signals of each local UAV,the imperfect information propagates through distributed control protocols,which makes the multi-UAV system vulnerable to uncertainties and thus severely degrades the cooperative performance.Due to the fact that this paper considers actual implementation of the system in the lab environment,it is of great importance to treat the poor information quality in the control law accordingly.To address that problem,[24]proposed an adaptive stabilization control for cyber-physical systems against measurement noises.Moreover,a distributed adaptive leaderless control for multi-agent systems was proposed in[25].However,current results in[24,25]require that the measurement noises are restricted to certain simple types.More importantly,these papers only theoretically analyzed the measurement noise problem in the cooperative control,but few results have been experimentally validated.

In this paper,we aim to design the cooperative control of multiple UAVs under measurement noises with theoretical analysis and physical experiments.To do this,we first model the dynamics of each individual UAV and its measurement noises.Based on the sliding mode control design,we propose a distributed control protocol that stabilizes all signals in the closed-loop multi-UAV systems and ensures that the consensus errors are uniformly ultimately bounded.Moreover,we use local information to define the trustworthiness[26–28],based on which we tune the edge weights to compensate for the negative effect from noisy measurements.In addition,we bridge the gap between the theoretical framework and the physical experiment and implement our results by using Crazyflie 2.0 platform.In our experiments,we utilize the motion capture system(VICON)to coordinate UAVs through the communication topology based on a master-slave model.Furthermore,a hierarchical motion control state machine is designed in a distributed fashion and implemented as a software solution based on robot operating system environment(ROS).To ensure low latency and smooth control loop,data pipeline is implemented as a multi-threaded routine specifically tailored for the high-speed control requirements of dynamically rich UAVs.Several experiments are designed to validate the effectiveness of our algorithms.

The remaining parts of this paper are outlined as follows.In Section 2,some preliminaries on graph theory are provided.In Section 3,the dynamics of UAV are detailed.In Section 4,the controller for coordinating UAVs is proposed,and its stability analysis is carried out.In Section 5,the trustworthiness based approach is proposed to tune the edge weight.The experimental environment is detailed in Section 6,and the experimental results are given in Section 7.Finally,the conclusion is contained in Section 8.

2 Preliminaries on graph theory

In this section,we briefly give some preliminaries on graph theory that will be used in our analysis and experiments.

De finition 1Let graph G be the pair

where V denotes vertices(nodes)of a graph and E denotes the edges of a graph.In that context V can be represented as

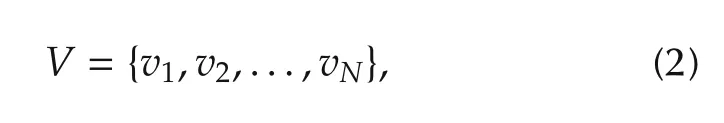
where viis vertex(node)i of a graph.Nodes are connected by links(edges).Edge E is defined as

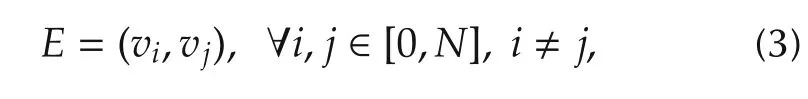
which is a connection between two nodes i and j.

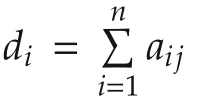
3 Quadrotor dynamics

When dealing with UAVs,states used for expressing dynamics are position ξi,velocityattitude ηiand angular rate˙ηi.Quadrotor dynamics are expressed as follows

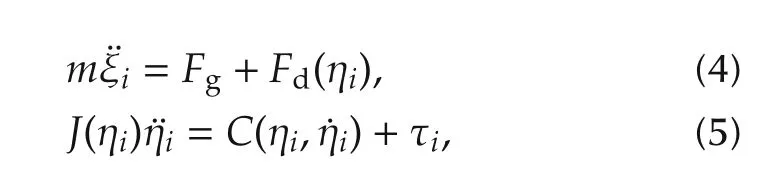
where Fgis a gravitational force,and Fdis a nonlinear input that depends on the attitude,ηare rotational states(roll,pitch and yaw),and τ is the torque generated by propellers.

Note that the focus of this paper is on efficiency of the cooperative control policy rather than the design of effective dynamical controller for a single UAV.Without the loss of generality,certain simplifications are used.UAVs that we worked with are very lightweight(27 g)which permits us to linearize the dynamical system.Consensus controller will be tested only in the x-y plane.After the linearization around the equilibrium point(similar to[29]),systems(4)and(5)can be reduced to the following form:

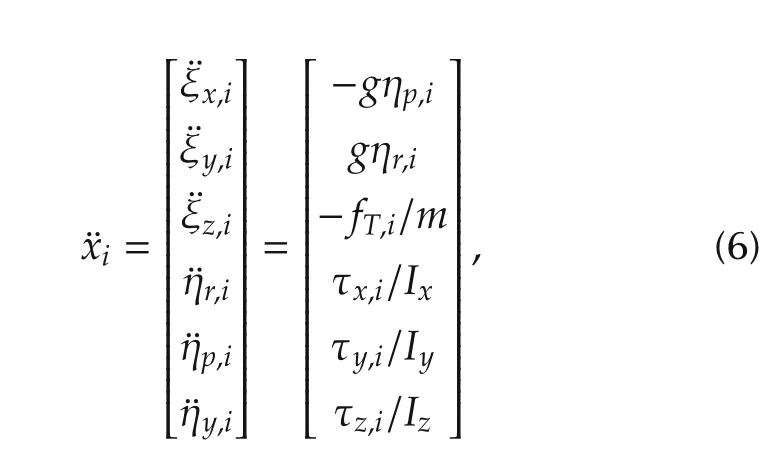
where the system state xiis given as

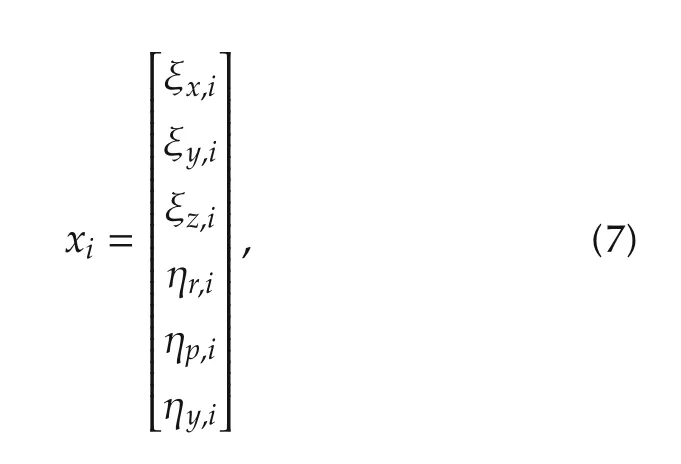
where Ix,Iyand Izdenote the idealized moments of inertia for each axis and m is the mass of the UAV.After separating the input terms from the state transition matrix,we can change(6)into

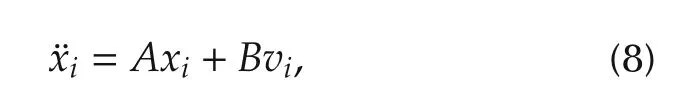
where

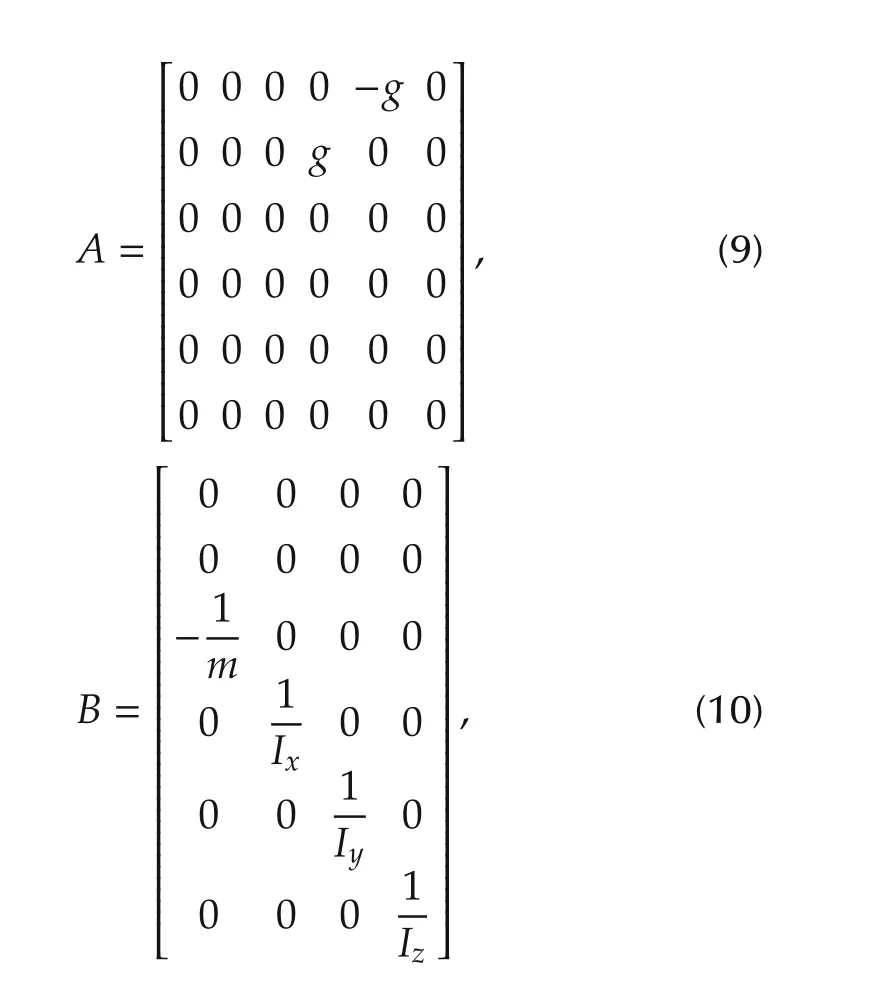
and the control input is

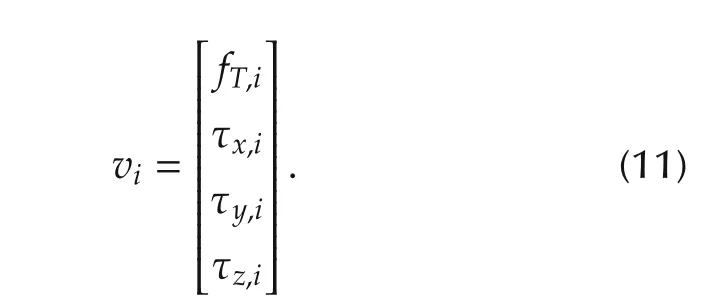
Considering that there are N UAVs in this paper,we present the system dynamics in a global form as

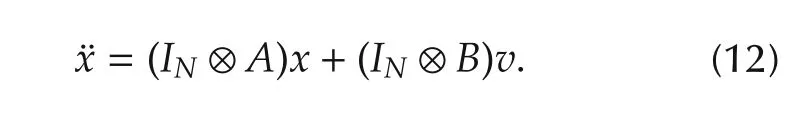
To model the group of agents with distributed information we use the graph theory.In the light of that,every link of the graph represents communication capability between connected agents,while nodes represent dynamical agents.The objective of this paper is to make the follower quad rotors in the graph G track the desired trajectory based on the distributed information,where the trajectory is generated by the leader.

4 Position consensus controller

We introduce Δias a displacement of UAVi from the center of the formation.Different combinations of Δican now be used to encode various formations.x0is the agent leader and is directly linked to those agents that have non-zero pinning gain gi.The reference is generated by the leader and is effectively transmitted to the whole system through the distributed communication network.

The neighbourhood error is defined as

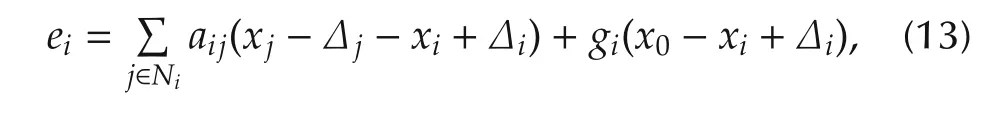
and neighbourhood time derivative of the error

If we assume that the position of the leader(x0)and the relative positions between the agents(Δi,∀i)are not changing during the experiment then

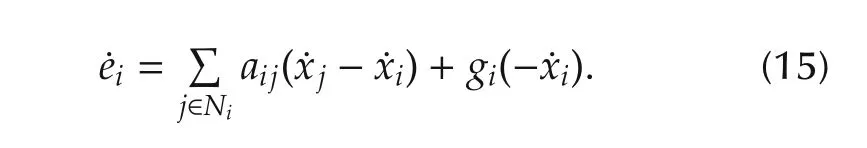
The alias of ideal positions displaced by Δiis introduced

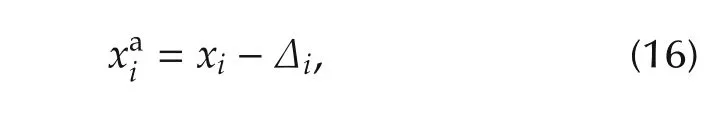
for i=1,2,...,N.From(16),position errors between the two agents are given as

From(17),the neighbourhood error defined in(13)now has the form

Definewith all N elements ones.The global forms of(18)and(19)are now expressed as

In order to further develop the discussion on that hypothesis,the second order error dynamics is first calculated

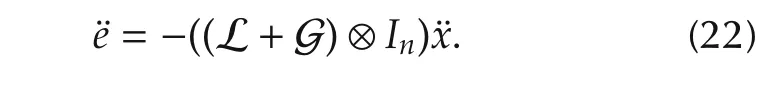
Plugging(12)in(22)gives

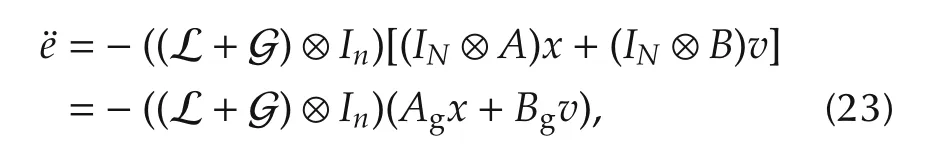
whereandWithout the loss of generality,further simplification is introduced

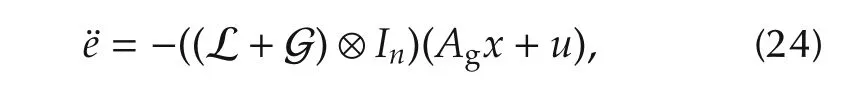
where u=Bgv is defined as the global vector of inputs.

To drive both position and velocity to zero,we use the sliding mode control and define the sliding mode error as

where Λ is positive definite.From[30],e is bounded as long as r is bounded.Let λ =diag{λi}be N dimensional diagonal matrix with λion the diagonal,each corresponding to one agent.Then Λ = λ ⊗In.Taking the time derivative of(25)yields

By using Kronecker rule(A⊗B)(C⊗D)=(AC)⊗(BD)(under the assumption that dimensions of A,B,C,D allow multiplications AC and BD),we introduce the following for convenience

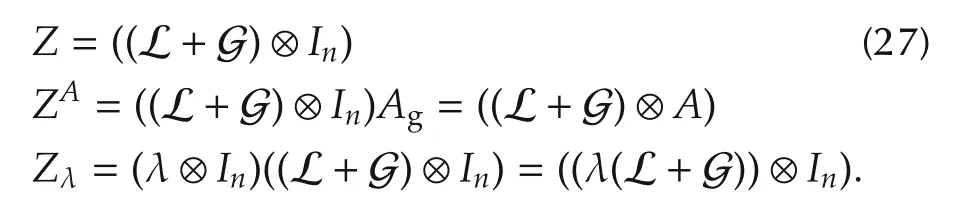
Rewrite(26)as

Based on the undirected graph topology,we make some assumptions useful for the control design.

Assumption 1L is irreducibly diagonally dominant matrix.

Assumption 2G has at least one diagonal entry.

It is not restrictive to make Assumptions 1 and 2,since many practical multi-agent systems fall under that category.

We introduce the control law locally and globally as

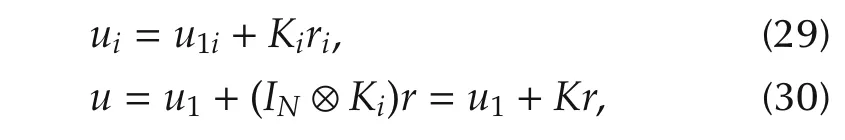
where matrix Ki=Kj,∀i,j is used for control design.Assume that u1cancels first two terms in(28).u1is specified later in the theorem.Under that assumption rewrite(28)in the global form

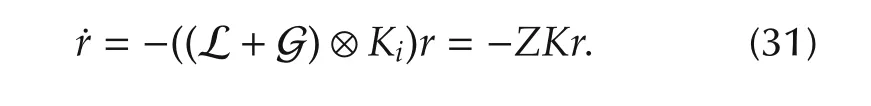
Lemma1Let Assumptions1 and 2 hold.If wedefine

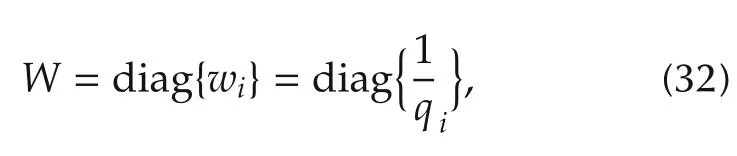
where

then,both W and Q=W(L+G)+(L+G)TWare positive definite.Additionally,if Q is positive definite then Q⊗Inis also positive definite.Q=W(L+G)+(L+G)TW.

ProofThe first assertion follows the results in[9,31].For the second assertion,we obtain that eigenvalues of a matrix generated by Kronecker product are cross-products of all possible combinations of eigenvalues from matrix Q and In.Both Q and Inare positive definite and corresponding eigenvalues all positive.This completes the proof. □

Assumption 3Let¯x be the measurement of ideal state vector x

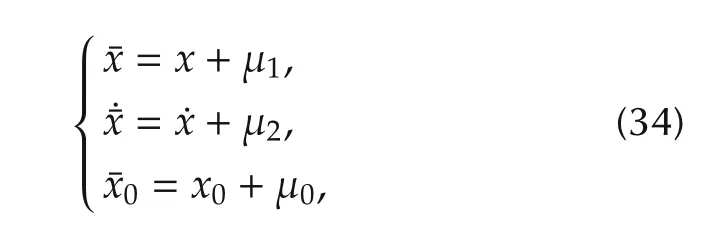
then define the bound on sensor noise

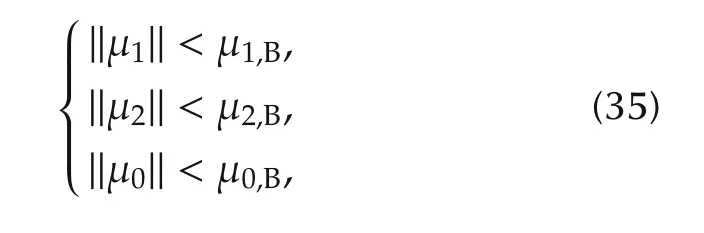
where μ0,Bdenotes the measurement error of leader’s position.

Sliding mode error injected with noises is

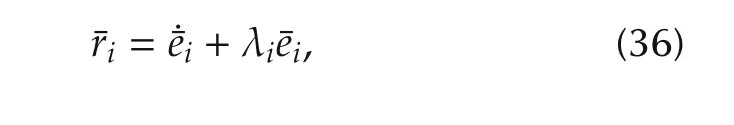
where

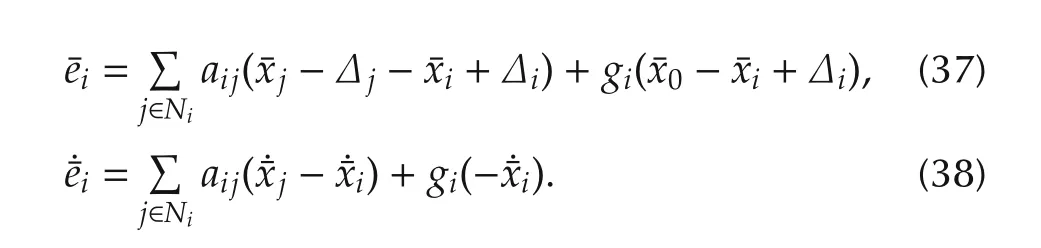
The global form of noisy error is

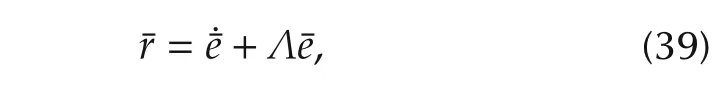
where

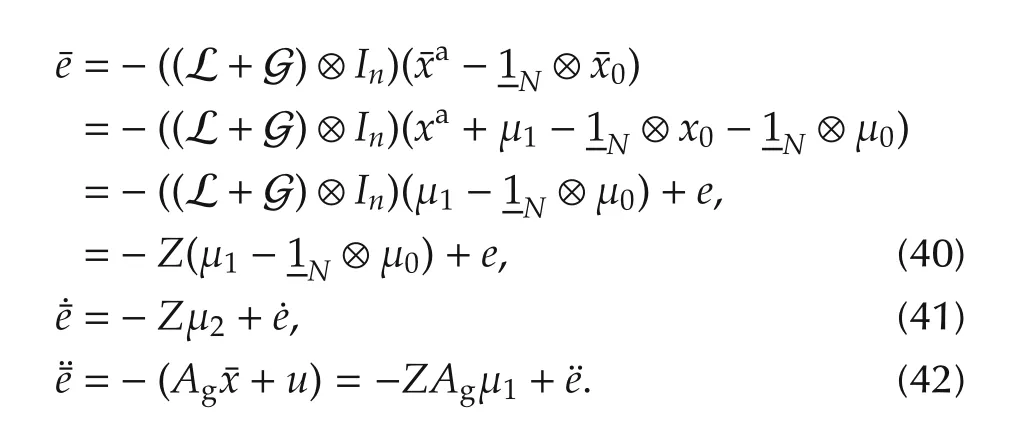
Extracting the ideal sliding mode error from the measured error gives

Substituting(42)and(41)into(26)yields

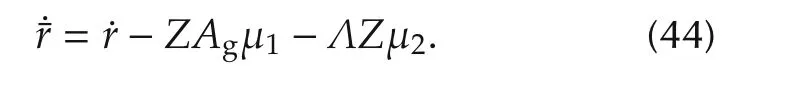
Definition 2The signal z(t)is said to be uniformly ultimately bounded(UUB)with the ultimate bound b,if given positive constants b and c,for every d∈(0,c),there exists T(d,b),independent of t0,such that

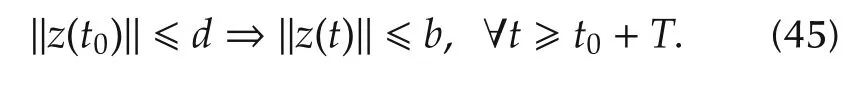
Here,we propose our distributed consensus control for UAVs in the following theorem.

Theorem 1Let Assumptions 1–3 hold.Define the sliding mode error dynamics as(26).Select the control policy for the local agent as

Assume that λi= λj,∀i,j,(46).Consider the error dynamics(31)and design matrices Q and R.Pick following control gain

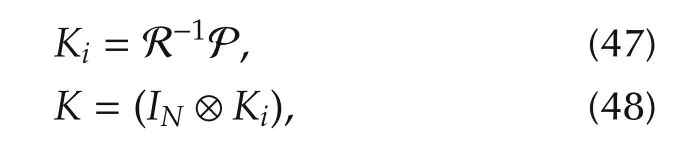
where P is the unique positive definite solution of control algebraic Riccati equation

The control law(46)with the gain(47)guarantees asymptotic stability for(31).Moreover it stabilizes the system(12)and makes the ideal tracking error(13)UUB.

ProofLet eigenvalues of(L+G)be νi= αi+jβi.Matrix L+G has αi＞ 0 because of Assumption 1 and 2.System(31)is asymptotically stable if matrices−νiKiare asymptotically stable(see[9]).Since P＞0,R＞0 and αi＞ 0 it follows that matrix −νiKiis Hurwitz and(31)is asymptotically stable.From Lyapunov theory,the stability condition for(31)is equivalent to

where Q＜0 and P＞0,PT=P,and K from(48).(50)is equivalent to

To prove stability in the presence of noisy measurements,consider following Lyapunov function candidate for multi-agent systems in global form

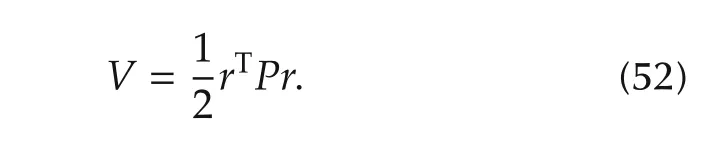
Differentiating(52)with respect to(26)yields

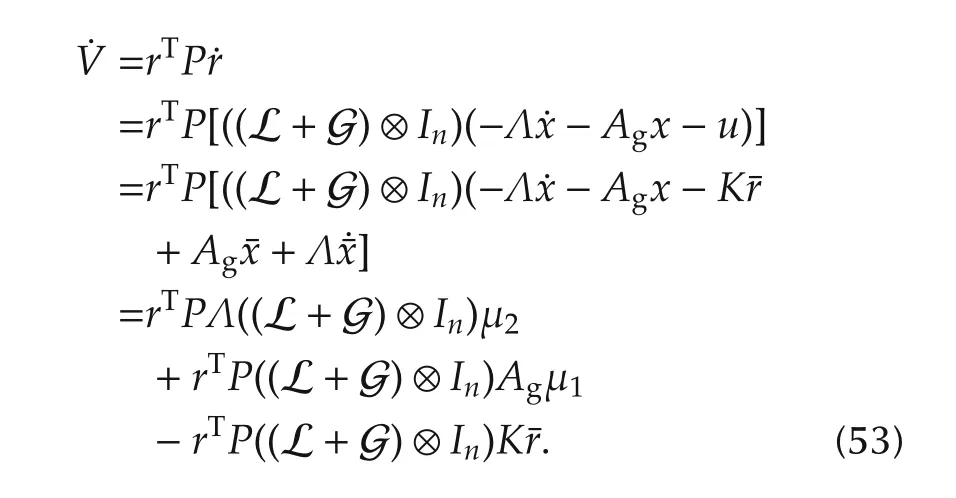
For brevity,we use(27).Combined with(43)gives

Note that the upper bound on˙V can be found through the norm algebra and the bounds that are previously assumed to limit the measurement noise vectors.To be specific,from(54),we have

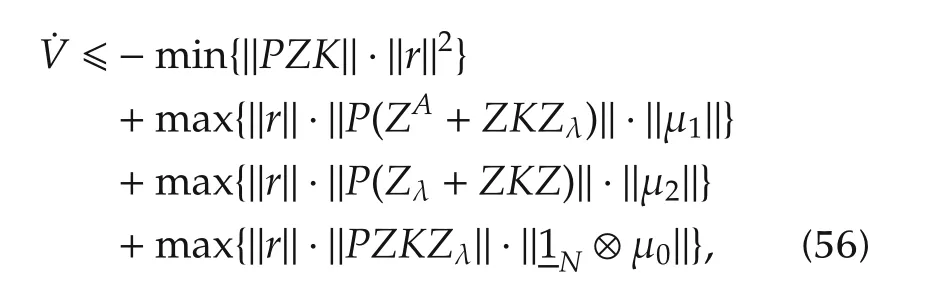
based on which(56)is changed into

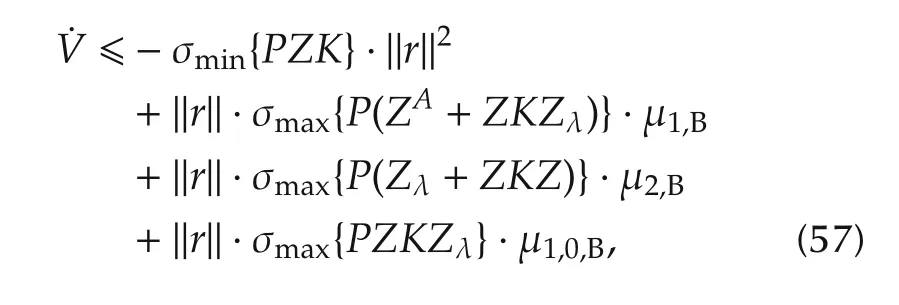
where σmax(M)and σmin(M)denote maximum and minimum eigenvalue of matrix M.From(57),it is clear that ˙V is always negative for

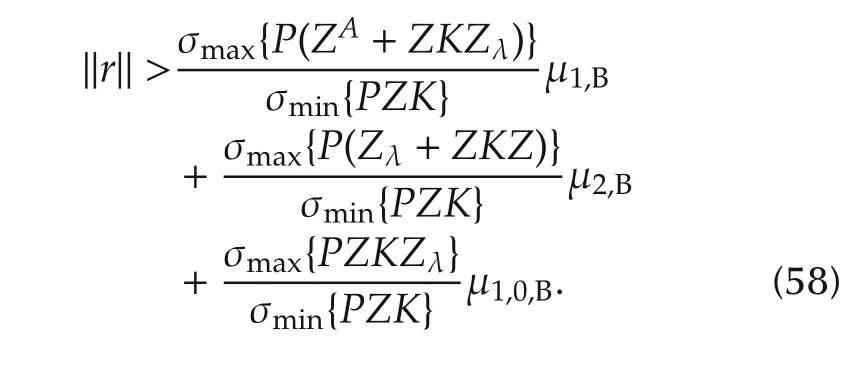
Moreover,if r is outside the bounding set given in(58),our controller will eventually drag the error inside the set.In other words,the sliding mode error r is bounded to a set which makes all the signals in the closed-loop multi-agent system UUB. □

The controller drags all aliasesfor i=1,...,N to the center of the formation.If all aliases are in the center of the formation,no action from the controller is required.Neigh bour hood errors quantify the spatial disharmony of the formation.The controller determines an action uiof the agent i such that it recovers consensus.Λ is a tuning parameter.As given,controller resembles well known standard PD controller.

5 Modifying edge weights based on trust

In this section,it is shown how UAVs in the graph can distributively modify the graph weights based on their measure of trustworthiness of the neighbors.The purpose is to maintain the consensus by eliminating negative influence of stubborn agents or extremely noisy measurement imposed on the local agent.

The trust that agent i has for agent j can be calculated as deviation from the intended average state of neighboring agents

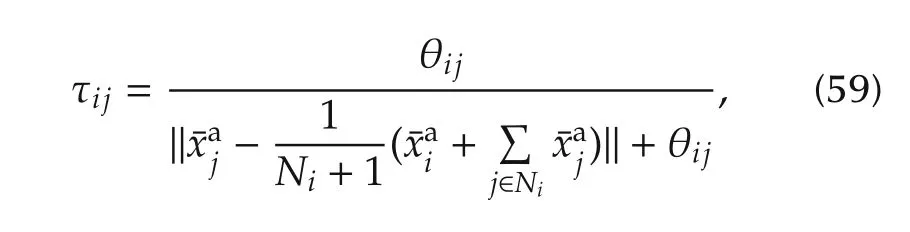
where θijis a certain positive constant that serves as a threshold value.From(59),when the local agent j approaches the average of the neigh bourhood agents,the trust value τijapproaches one;otherwise, τijapproaches zero.With this trust metric,we further propose a mechanism to modify the graph weights.To this end,we use the differential equation

where η is a certain positive constant.To take into account the trust value calculated for neighbors,the controller(46)isnow revisited by weighting all edge weights aijby dij.That is all occurrences of aijin(46)arereplaced by dijaij.

6 Experimental environment

Fig.1 shows an entire system designed at UTA Research Institute for testing distributed controllers on UAVs.Basic four elements are VICON,Crazyflie 2.0 UAVs,and the workstation that runs master program.Master is implemented as ROS package and it handles consensus controller calculation as well as local manipulation over UAVs.

As already mentioned,Crazyflie 2.0 is used as UAV and it communicates with master workstation using radio transceiver.In order to have reliable feedback information,we use motion capture system VICON.Data is transmitted to master through wireless local area network.Such communication architecture enables consensus controller to send the control commands to UAVs at 200 Hz,which is more than sufficient.

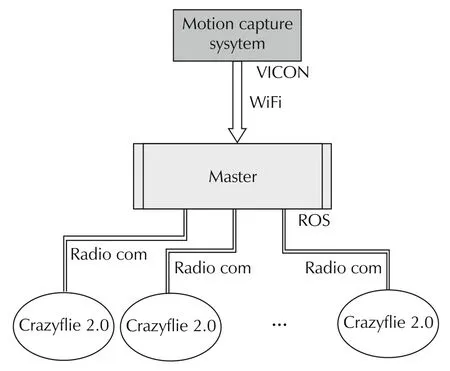
Fig.1 Motion capture and communication topology based on master-slave model architecture.

6.1 Crazy flie 2.0

Crazyflie 2.0 is a commercially available UAV suitable for research and development.It is created by Bitcraze AB.We use their hardware and modify the firmware to implement our control laws.IMU data collection,four motors with corresponding PWM modules and communication with radio(nRF51822)is all handled by micro controller(STM32F405).Attitude controller is implemented on firmware side rather than on master/server.It uses inputs from outer control loop(commanded velocities in all three dimensions and commanded yaw rate)and IMU data to stabilize UAV and to drive it to the desired position.Desired values are received from nRF51822,previously sent from the master.The output of attitude controller are signals that determine PWM cycle duty and eventually produce propeller thrusts and torques.For more hardware and construction details,as well as for a simplified mathematical model of Crazyiflie 2.0 refer to the official website[32].

6.2 Master workstation

Fig.2 shows the software architecture that is executed on the master workstation.The master controller is a ROS node that manages general control of all UAVs.Each UAV is controlled by individual outer loop controller.

The master controller is,in fact,a mission planner.It commands different tasks to UAVs by communicating with corresponding position controller.It also listens to external user input to allow manual task switching,manual takeoff,manual landing,and manual emergency landing.State machine seems to be a plausible design solution for master controller,considering its current function of switching states.As Fig.3 clearly shows,there are three different states in state machine.In way point tracking state,master controller simply sets way points to position controllers.Consensus controller is slightly more complex,as generalized formation error for each UAV has to be recalculated at every iteration.The idle state is active when all Crazy flies are off.It is important to notice that user has the control over whole state machine which is a security requirement.

Fig.2 Distributed multi-threaded software architecture with data pipeline.

The described procedure can be broken down into the following main steps:

Step 1Check the link quality.If link quality is low proceed to Step 7.Otherwise continue to Step 2.

Step 2Collect data from VICON,distribute information to agents according to adjacency matrix.

Step 3Update trust values and apply them to modify adjacency matrix.

Step 4Call local distributed controllers.Send calculated roll,pitch,yaw and thrust commands to each agent.

Step 5Calculate PWM locally on each agent and generate forces.

Step 6If no user interrupt,go back to Step 1.Otherwise go to Step 7.

Step 7Start landing sequence.Land.

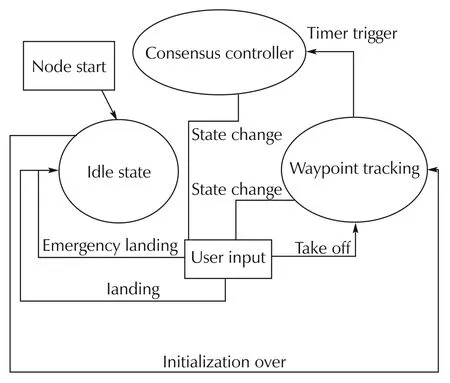
Fig.3 Distributed hierarchical motion control state machine.

7 Flight tests

Three flight tests shown in Fig.4 are carried out in this section,where different adjacency matrices are picked.For each experiment,we show two plots,x position and y position for all three UAVs.The desired reference is set(0,0,0.7)and disturbance is applied to one of three UAVs to test the behaviour of the group.To be specific,we push the UAV away from the point of global equilibrium imposed by consensus controller.Displacements from the desired reference are Δ1=(−0.5,0.5,0.0),Δ2=(0.5,0.5,0.0),and Δ3=(−0.5,−0.5,0.0).Note that in the experiment,we define the virtual input u as

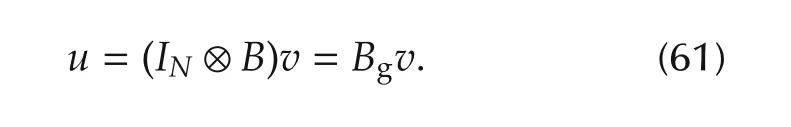
Technical control vector v can now be calculated from virtual inputs u through

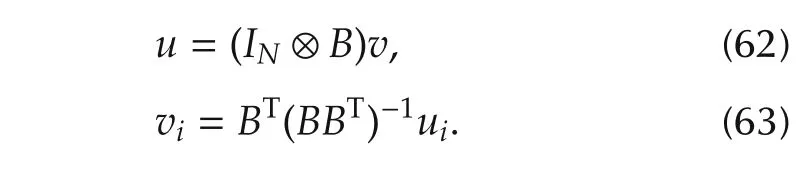
In fact,the ability to calculate v is not only a matter of convenience,but rather a necessity,since v is the command vector that is transmitted to UAV agents.uiis a distributed control signal(46).In the first 5 seconds,altitude control is applied to take off UAVs,and after that our consensus controller is activated.

Fig.4 Photograph of the experiment during consensus.

7.1 Experiment 1

In this case,we define the adjacency matrix as

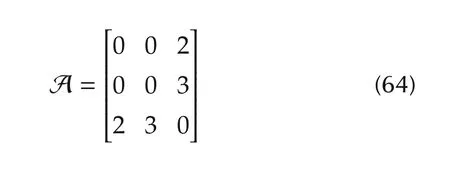
and the pinning gains as g2=3 and g1=g3=0.After applying our controller,the experimental results are presented in Figs.5 and 6,where UAVs 1–3 are labelled in red,blue,and green.Here,UAV 1 is the agent that is injected with disturbances.In this experiment,UAV 1 moves away from the consensus due to disturbances,while UAVs 2 and 3 try to follow.From(64),UAV 3 strictly follows movements of agent 1 in order to keep consensus,since it has direct link to agent 1.Note that UAV 2 is less responsive to position change of agent 1 due to the fact that agent 2 is connected to the leader.

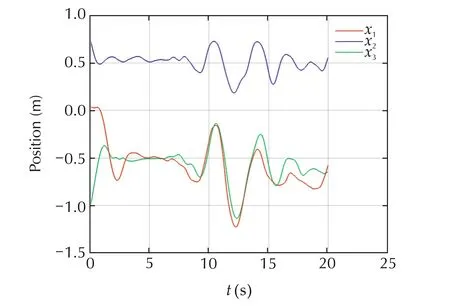
Fig.5 Experiment 1,positions x of UAVs.

Also notice that UAV 1 is first sent way out of desired position at around 9th second.At the very peak,when UAV 1 is more than 0.5m away from desired position,UAV 3 does not follow UAV 1 to the extreme deviation because it has lost trust in UAV 1(a13was close to 0).The fact that trajectories of UAVs 1 and 3 have slightly different shapes at that point confirms that(Fig.6).As UAV 1 returns and distance between UAVs 1 and 3 is back as expected,trust increases and consensus is reestablished.

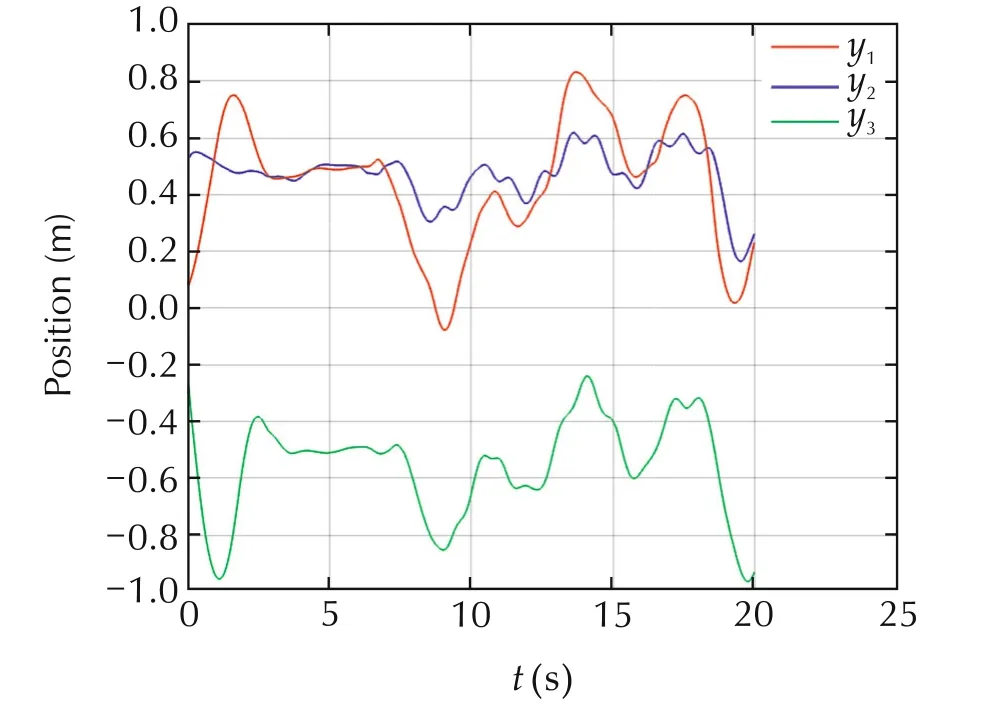
Fig.6 Experiment 1,positions y of UAVs.

7.2 Experiment 2

Here,we define the adjacency matrix as and the pinning gains as g2=3 and g1=g3=0.Adding a direct link between agents 1 and 2 makes UAV 2 a bit more responsive.Formation control in Figs.7 and 8 is better compared to that in the previous experiment.

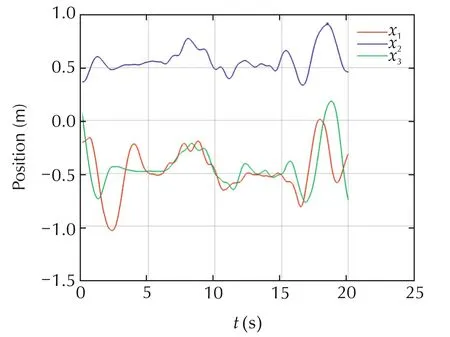
Fig.7 Experiment 2,positions x of UAVs.

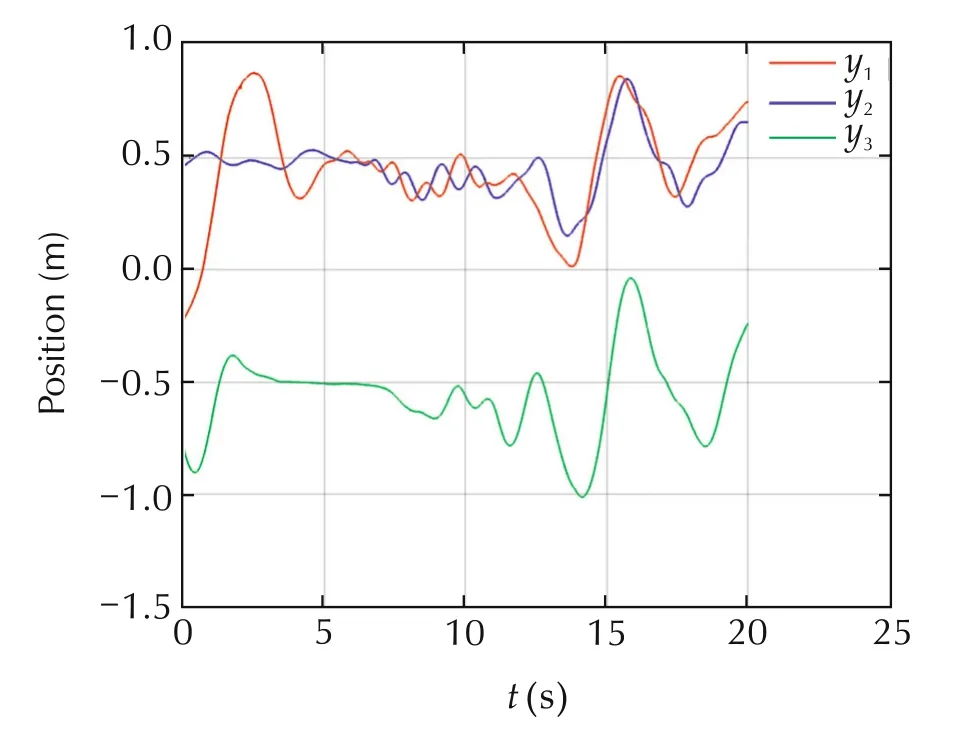
Fig.8 Experiment 2,positions y of UAVs.

7.3 Experiment 3

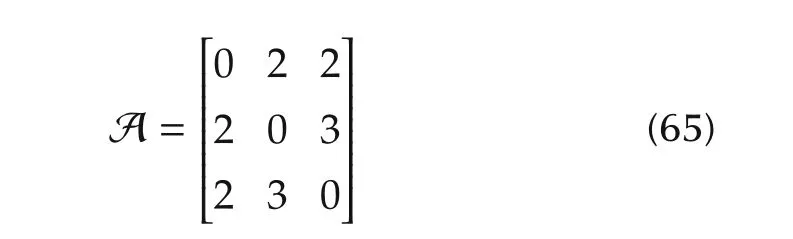
In the final experiment,the adjacency matrix is designed as

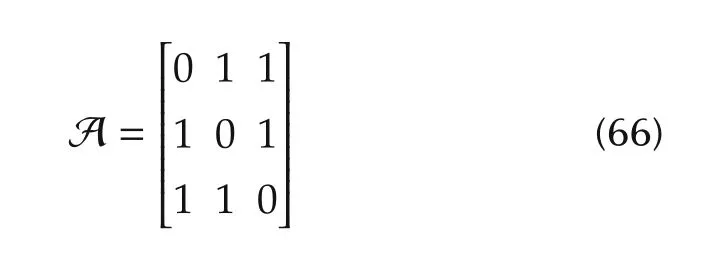
and pinning gains are given as g1=g2=g3=1.Compared to the previous experiments,(66)gives the best performance,as shown in Figs.9 and 10.Such results are expected because the graph is dense and weights are not giving preference to any neigh bouring agent.

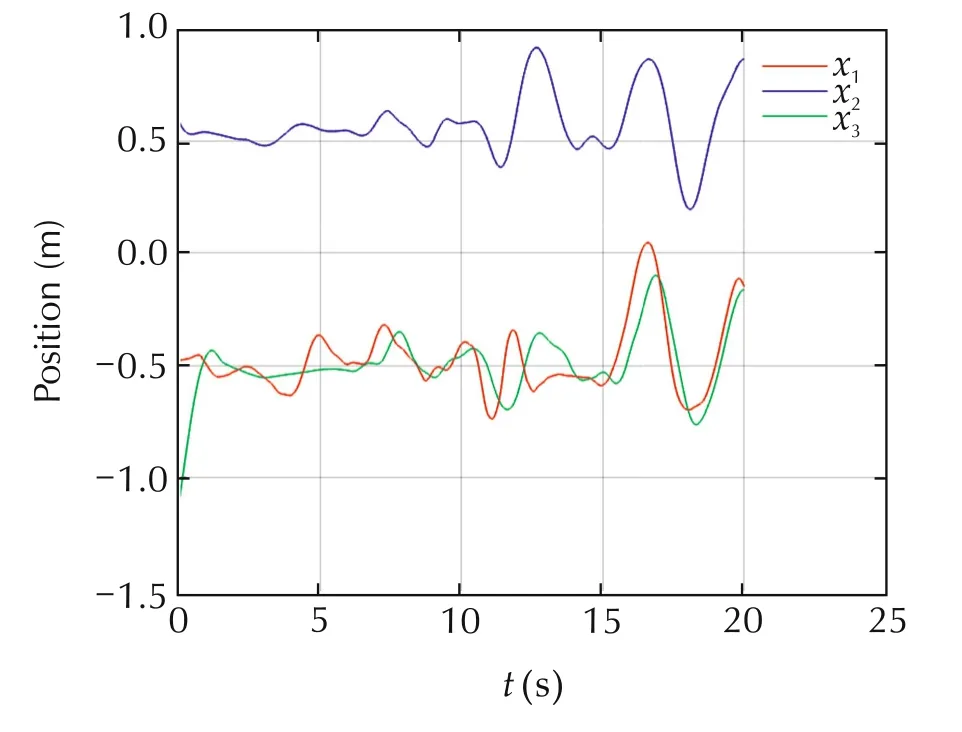
Fig.9 Experiment 3,positions x of UAVs.

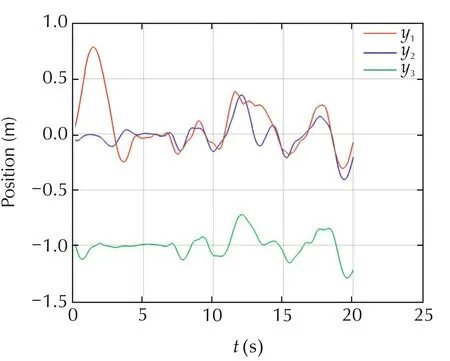
Fig.10 Experiment 3,positions y of UAVs.

8 Conclusions

Consensus control design introduced in this paper is effective in keeping a group of UAVs in the formation.Confirmation is given by using Lyapunov theory to prove the stability of the group and later in the experimental environment on the system of multi UAVs.

It is shown that the robustness of consensus depends highly on the graph topology.In that aspect,fully connected graphs will provide better basis for firm consensus control.Unfortunately,it is often the case that practical multi-agent network topology is inherent to the system to which control is applied.In other words,while designing controller,graph is predefined and cannot be changed in favor of better control.However,one thing we can do is to update the values of the links that are present based on the trustworthiness of a neigh bouring agent.Our approach achieves that.

Due to certain practical assumptions about dynamics of the nano UAV and by restricting experiments to as low flight,we were able to make some reasonable simplifications on the dynamical model of the UAV.That allowed for more transparent design of the consensus controller in the light of measurement noises imposed on the system.Future work should extend current design to the domain of non-linear control,allowing for dynamically rich experiments and treat the measurement noise with advanced tools such as distributed Kalman filter.

[1]U.S.Air Force Research Laboratories.UAV Cooperative Decision and Control;Challenges and Practical Approaches.T.Shima,S.Rasmussen(eds.).Philadelphia:SIAM.2009.

[2]R.M.Murray.Recent research in cooperative control of multivehicle systems.Journal of Dynamic Systems Measurement and Control–Transactions of the ASME,2007,129(5):571–583.

[3]Z.Qu.Cooperative Control of Dynamical Systems:Applications to Autonomous Vehicles.London:Springer,2009.

[4]A.Das,K.Subbarao,F.L.Lewis.Dynamic inversion with zerodynamics stabilisation for quadrotor control.IET Control Theory&Applications,2009,3(3):303–314.

[5]A.Das,F.L.Lewis,S.Subbarao.Backstepping approach for controlling a quadrotor using neural network.Journal of Intelligent and Robotics Systems,2009,56(1):127–151.

[6]F.L.Lewis,S.Jagannathan,A.Yesildirak.Neural Network Control of Robot Manipulators and Non-linear Systems.Boca Raton:CRC Press,1998.

[7]P.Wang,Z.Man,Z.Cao.Dynamics modelling and linear control of quadcopter.International Conference on Advanced Mechatronic Systems,Melbourne:IEEE,2016:498–503.

[8]G.V.Raffo,M.G.Ortega,F.R.Rubio.An integral predictive/nonlinear H∞control structure for a quadrotor helicopter.Automatica,2010,46(1):29–39.

[9]F.L.Lewis,H.Zhang,K.Hengster-Movric,et al.Cooperative Control of Multi-agent Systems:Optimal and Adaptive Design Approaches.London:Springer,2013.

[10]R.Olfati-Saber,J.A.Fax,R.M.Murray.Consensus and cooperation in networked multi-agent systems.Proceedings of the IEEE,2007,95(1):215–233.

[11]W.Ren,R.W.Beard,E.M.Atkins.Information consensus in multivehicle cooperative control.IEEE Control Systems,2007,27(2):71–82.

[12]Randal W.Beard,Timothy W.McLain.Small Unmanned Aircraft:Theory and Practice.Princeton:Princeton University Press,2012.

[13]S.Khoo,L.Xie,Z.Man.Robust finite-time consensus tracking algorithm for multirobot systems.IEEE Transactions on Mechatronics,2009,14(2):219–228.

[14]X.Xu,L.Liu,G.Feng.Consensus of single integrator multiagent systemswith directed topology and communication delays.Control Theory and Technology,2016,14(1):21–27.

[15]Y.Kuriki,T.Namerikawa.Consensus-based cooperative formation control with collision avoidance for a multi-UAV system.American Control Conference,Portland:IEEE,2014:2077–2082.

[16]M.Yan,X.Zhu,X.Zhang,et al.Consensus-based three dimensional multi-UAV formation control strategy with high precision.Frontiers of Information Technology&Electronic Engineering,2017,18(7):968–977.

[17]J.Wang,X.Nian,H.Wang.Consensus and formation control of discrete-time multi-agent systems.Journal of Central South University of Technology,2011,18(4):1161–1168.

[18]A.Das,F.L.Lewis.Cooperative adaptive control for synchronization of second-order systems with unknown nonlinearities.International Journal of Robust and Nonlinear Control,2011,21(13):1509–1524.

[19]J.Thunberg,W.Song,Y.Hong,et al.Distributed attitude synchronization using backstepping and sliding mode control.Control Theory and Technology,2014,12(1):48–55.

[20]H.Zhang,F.L.Lewis,A.Das.Optimal design for synchronization of cooperative systems:state feedback,observer and output feedback.IEEE Transactions on Automatic Control,2011,56(8):1948–1952.

[21]D.Vrabie,F.L.Lewis.Adaptive dynamic programming for online solution of azero-sum differential game.Journal of Control Theory and Applications,2011,9(3):353–360.

[22]K.G.Vamvoudakis,F.L.Lewis.Multi-player non-zero-sum games:Online adaptive learning solution of coupled Hamilton-Jacobi equations.Automatica,2011,47(8):1556–1569.

[23]K.G.Vamvoudakis,F.L.Lewis.Online solution of nonlinear two-player zero-sum games using synchronous policy iteration.International Journal of Robust and Nonlinear Control,2012,22(13):1460–1483.

[24]T.Yucelen,W.M.Haddad,E.M.Feron.Adaptive control architectures for mitigating sensor attacks in cyber-physical systems.American Control Conference,Boston:IEEE,2016:1165–1170.

[25]E.Arabi,T.Yucelen,W.M.Haddad.Mitigating the effects of sensor uncertainties in networked multiagent systems.American Control Conference,Boston:IEEE,2016:5545–5550.

[26]J.S.Baras,T.Jiang.Trust evaluation in anarchy:a case study on autonomous networks.Proceedings of IEEE INFOCOM,Barcelona:IEEE,2006:835–846.

[27]J.S.Baras,T.Jiang.Cooperation,trust and games in wireless networks.Symposium on Systems,Control,and Networks,Berkeley:Birkhauser,2005:183–202.

[28]T.Jiang,J.S.Baras.Graph Algebraic Interpretation of Trust Establishment in Autonomic Networks.Maryland:University of Maryland,2010.

[29]Y.Kuriki,T.Namerikawa.Formation control of UAVs with a fourth-order flight dynamics.The 52nd IEEE Conference on Decision and Control,Florence:IEEE,2013:6706–6711.

[30]J.-J.E.Slotine,W.Li.Applied Nonlinear Control.Englewood Cliffs:Prentice Hall,1991.

[31]Z.Qu.Cooperative Control of Dynamical Systems:Applications to Autonomous Vehicles.New York:Springer,2009.

[32]Bitcraze.https://www.bitcraze.io/.