大气湍流等效相位屏的仿真研究*

徐瑞超，高 明

(西安工业大学 光电工程学院， 西安 710021)

光在大气环境中传播时，由于大气温度和压强的变化会产生大气折射率的随机扰动，从而发生光束波前畸变.在激光通信领域，大气湍流对激光传输的影响会引起外场光电设备的非正常工作，因此了解湍流的变化，掌握激光在大气湍流中的传输特性对于激光通信中提高光束的光通量大有作用，所以需要对大气湍流进行相关方面的研究.在大气湍流的相关研究中，通常采用数值方法对大气湍流相位屏进行模拟仿真，其具有清晰直观的优点.模拟大气湍流等效相位屏的数值方法可以分为两大类：① 功率谱反演法，由Mcglamery[1]提出，其是通过大气湍流的功率谱密度函数得到扰动的大气湍流相位分布.文献[2]利用功率谱反演研究了一个完整的自适应光学激光大气传输的相位补偿系统的数值模拟.文献[3-4]从产生大气湍流随机相位屏的功率谱反演法原理出发，分析了均匀采样造成的随机相位屏大量低频信息泄漏的不足，并且对大气湍流功率谱非均匀采样进行了研究，认为其可以有效改善传统功率谱反演法低频采样严重不足的缺陷，实现高精度的大气湍流相位屏的模拟；② 采用正交的泽尼克多项式法来模拟大气湍流，这种方法对于大多形式的湍流功率谱研究较少，而在Kolmogrov 谱的模拟上效果比较显著.文献[5]利用泽尼克多项式对大气湍流相位屏波前补偿系统需要独立的改正数进行了解析描述.文献[6]基于泽尼克多项式对大气湍流波前相位畸变进行了模拟.文献[7]通过泽尼克多项式法仿真了大气湍流相位屏并利用相位结构函数进行了验证.以上的研究均使用单一方法对大气湍流相位屏进行了模拟，对于整个空间频率大气湍流适用哪种方法的研究较少.

因此，本文分别使用功率谱反演法和泽尼克多项式展开法模拟仿真了大气湍流畸变波前相位屏，数值模拟了两种方法产生的相位屏在不同参数下的相位结构函数曲线，通过比较相位结构函数与理论结果的差异来对比两种方法在模拟大气湍流相位屏不同空间频率部分的优缺点.

1 大气湍流相位屏模拟方法

1.1 谱反演法

采用谱反演法模拟大气湍流相位屏，首先假设一个复高斯随机数矩阵，然后使用大气湍流功率谱对其进行滤波处理，最后通过傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)得到大气湍流中大气扰动的相位分布[8].

假设有一零均值，其单位方差复值高斯随机过程a(k)满足

〈a(k)a(k′)〉=δ(k-k′)

(1)

式中：k,k′均为空间频率；δ为Dirac函数.进一步假定a(k)是Hermitian对称的，即

a(-k)=a*(k)

(2)

其中a*(k)为Hermitian共轭随机过程.

用滤波函数G(k)来得到符合湍流大气统计特性的等效相位屏S(r)，G(k)反映了相位屏上空间频率为k的起伏分量幅度的期望值.S(r)的自相关函数为

exp(ik·r-ik′·r′)dkdk′

(3)

式中：r,r′均为空间任意点；S*(r′)为等效相位屏的共轭；G*(k′)为相位屏上空间频率为k′的起伏分量幅度的共轭期望.

利用式(1)，将式(3)化简为

(4)

由于〈S(r)S*(r′)〉是大气湍流等效相位屏起伏的相关函数，所以根据Rytov理论可得复相位变换为

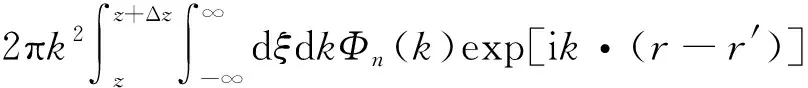
(5)

式中：z为湍流中任意点；L为空间传输距离；Φn(k)为大气折射率功率谱密度函数;ξ为比例系数；Δz为湍流薄层厚度.比较式(4)和式(5)可得

(6)

由于G(k)为一个实值非负函数，且和Φn(k)一样各向同性，则

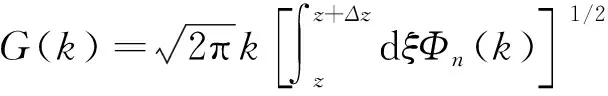
(7)

大气折射率谱采用vonkarman谱，大气折射率功率谱密度为

(8)

式中：Cn(h)为在斜程路径传输的湍流大气中随传输高度起伏的大气结构常数模型；h为接收机高度；k0,km均为谱参数.

采用简化模型，内、外尺度对模拟结果的影响并未展开讨论，所以内、外尺度统一取为内尺度l0=1 cm,外尺度L0=10 m.利用相关公式转化为

(9)

其中r0为大气相干长度.

应用谱反演法生成随机等效相位屏的公式为

(10)

利用谱反演法来模拟大气湍流等效相位屏，算法步骤为

① 首先生成一个复随机数矩阵k，其满足高斯分布；

② 依据大气折射率功率谱密度函数生成二维的功率谱密度函数矩阵Φ(k)；

(11)

④ 对矩阵Y(k)进行傅里叶逆变换，从而得到其空间域形式，即

Y(l)=IFFTY(k)

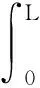
(12)

其中l为空间频率.

⑤ 对于式(12)得到的矩阵Y(l)，可以将其分解为实部和虚部.其实部和虚部均可以代表一种随机的大气湍流相位屏S1和S2,表达式为

S1=ReY(l)，S2=ImY(l)

(13)

1.2 泽尼克多项式法

泽尼克多项式由无穷数量的多项式完全集合组成，具有两个变量ρ和θ，其在单位圆内部连续正交.泽尼克多项式只有在单位圆的内部连续区域为正交，而在单位圆内部的离散的坐标上不具有正交性质.定义在单位圆上的泽尼克多项式极坐标表达式[9]为

(14)

(15)

(16)

式中：m为多项式的角向级次；n为多项式的径向级次.

泽尼克系数aj一般情况下被看作是具有零均值的Gauss 随机变量，设其系数向量为

A=[a2,a3,…,ap]T

(17)

协方差阵为

C=E[AAT]

=E(a2,a2)E(a2,a3),…,E(a2,ap)

E(a3,a2)E(a3,a3),…,E(a3,ap)

E(ap,a2)E(ap,a3),…,E(ap,ap)

(18)

其中协方差为

(19)

式中：D为光学系统的口径；Г[r]为伽马函数;δ为协方差参数；K为频率特征因子；n,n′分别为泽尼克数Zi,Zj的径向级次和角向级次，频率特征因子K依赖于Zi,Zj.由式(19)可见，在统计上泽尼克系数间的关系是相关的.所以很有必要引入Karhunen-Loeve(K-L)函数，即可通过有确定方差的随机量组合来表示大气湍流的随机波前，即

(20)

式中：Φ(r)为大气湍流的随机波前；bj为在统计独立中的随机系数；Kj(r)为K-L函数.

矩阵B为

B=[b1b2…bj]T

(21)

K-L函数目前为止还没有统一的解析式，但可以展开为Zernike多项式的形式，表达式为

(22)

式中：Zj(r)为泽尼克多项式；Vij为一般多项式.

将式(22)代入式(20)可得

(23)

比较式(19)和式(23)可见，矩阵A和矩阵B满足关系式：

A=VB

(24)

其中V为酉阵.

由于矩阵C为厄米阵，所以存在酉阵U从而使得UCUT为对角阵.同理矩阵C可分解为

C=VSVT

(25)

其中矩阵S为对角阵.令B=UA，故

E[BBT]=E[UAATUT]

=UE[AAT]UT=S

(26)

A=U-1B=UTB=VB

(27)

综上所述，应用泽尼克多项式展开法来模拟大气湍流等效相位屏，其重点在于系数aj的生成，生成步骤主要分为3步：

① 明确泽尼克多项式的阶数，得到协方差矩阵C.

② 分解协方差矩阵C的对角阵S，得到C=VSVT，其中V为酉阵.

③ 生成一个零均值随机向量，且其协方差矩阵C为对角阵S，从而得到多项式系数A=VB.

波前相位函数W(r,θ)可以应用正交的泽尼克多项式表示为

(28)

2 两种算法的模拟仿真比较

2.1 谱反演和泽尼克多项式的仿真实现

为了比较两种算法生成相位屏，特别选取了一定的大气湍流强度(使用大气相干长度r0表示)、不同口径D以及不同泽尼克多项式阶数N的数值，用两种算法分别模拟生成等效相位屏.将两种方法生成的等效相位屏作初步比较，然后再用相位结构函数进行分析比较.

图1(a)是谱反演法r0=0.01 m,口径宽度为0.3 m的波前相位图；图1(b)是泽尼克多项式法r0=0.01 m，N=100，D=0.3 m的波前相位图；图1(c)是泽尼克多项式法r0=0.01 m，N=200，D=0.3 m的波前相位图；图1(d)是泽尼克多项式法r0=0.01 m，N=400，D=0.3 m的波前相位图.

图2(a)是谱反演法r0=0.01 m,口径宽度为0.5 m的波前相位图；图2(b)是泽尼克多项式法r0=0.01 m,D=0.5 m,N=100的波前相位图；图2(c)是泽尼克多项式法r0=0.01 m,D=0.5 m,N=200的波前相位图；图2(d)是泽尼克多项式法r0=0.01 m,D=0.5 m,N=400的波前相位图.

图3(a)是谱反演法r0=0.1 m，口径宽度为0.3 m的波前相位图；图3(b)是泽尼克多项式法r0=0.1 m,D=0.3 m,N=100的波前相位图；图3(c)是泽尼克多项式法r0=0.1 m,D=0.3 m,N=200的波前相位图；图3(d)是泽尼克多项式法r0=0.1 m,D=0.3 m,N=400的波前相位图.

图1 不同参数下两种算法模拟生成的大气湍流相位屏

图2 不同参数下两种算法模拟生成的大气湍流相位屏

图4(a)是谱反演法r0=0.1 m，口径宽度为0.5 m的波前相位图；图4(b)是泽尼克多项式法r0=0.1 m,D=0.5 m,N=100的波前相位图；图4(c)是泽尼克多项式法r0=0.1 m,D=0.5 m,N=200的波前相位图；图4(d)是泽尼克多项式法r0=0.1 m,D=0.5 m,N=400的波前相位图.相位结构函数为

DΦ(r)=6.88(ρ/r0)5/3

(29)

式中：ρ为空间相干长度；r0为大气相干长度.

图3 不同参数下两种算法模拟生成的大气湍流相位屏

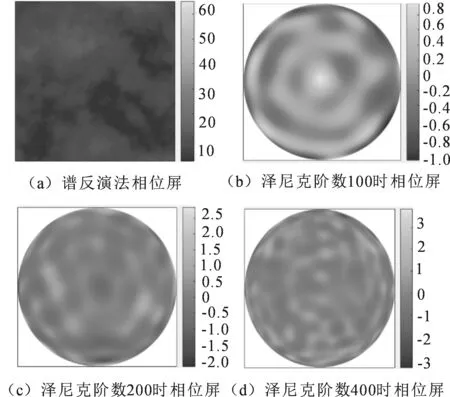
图4不同参数下两种算法模拟生成的大气湍流相位屏

Fig.4 Phase screen of atmospheric turbulence generated by two algorithms with different parameters

2.2 相位结构函数的比较评价

采用相位结构函数DΦ(r)和大气相干长度r0可以描述大气湍流中大气扰动的相位分布统计特性，对于 Kolgmgorov 谱而言，其相位结构函数的确定方法见文献[10].

图5为在波长为 6.328×10-7m ，相位屏大小为 256×256 pixel，采样点间隔为 0.003 m，相位屏间距为 500 m条件下，应用谱反演法模拟大气湍流相位屏时的相干长度r0=0.1 m，对应大气湍流结构常数为2×10-15的相位屏，并对相位屏叠加不同级次(1，2，3，4级)的次谐波后得到的相位屏相位结构函数.

图 6 为在波长为 6.328×10-7m，相位屏大小为 256×256 pixel，口径为 0.6 m 的条件下,采用不同阶次(5,100,200,400阶)Zernike多项式模拟相干长度r0= 0.1 m(中等强度)的大气湍流相位屏得到的相位结构函数.

a-理论；b-4次谐波；c-3次谐波 d-2次谐波； e-1次谐波；f-无谐波

a-理论；b-5阶泽尼克多项式；c-100阶泽尼克多项式；d-200阶泽尼克多项式；e-400阶泽尼克多项式

通过横向比较图1～4以及纵向比较图5和图6，可以看出：泽尼克多项式法产生的相位屏在低频空间部分比较吻合，但是在高频空间部分明显不如谱反演法更贴近理论曲线；通过增加泽尼克多项式的系数可以改善高频不足的现象，但不能完全消除影响；模拟仿真中应用泽尼克多项式法得到仿真结果明显慢于应用谱反演法；应用谱反演法产生大气湍流等效相位屏，低频部分会出现与理论值不吻合的现象，进行次谐波补偿产生较大计算量，而泽尼克多项式法相对来说具有计算量小的优点.

3 结 论

通过谱反演法和泽尼克多项式法对大气湍流相位屏进行了模拟仿真比较，并利用相位结构函数加以验证，得出结论为

1) 通过谱反演法生成的相位屏的结构函数高频部分与理论值吻合，但存在低频不足的现象，需要进行低频补偿来消除反演误差；

2) 泽尼克多项式法产生的相位屏的结构函数与谱反演法相反，在低频率空间部分其与理论值基本吻合，但在高频率空间部分则误差较大，可通过增加泽尼克多项式的阶数来改善高频不足的情况，随着多项式阶数的增加会引起计算量过大的问题.

3) 对于湍流的研究是为了能够及时了解湍流相位在大气中的分布，在实际研究工作中可以将两种方法结合考虑，减小了使用单一方式而造成的数值仿真误差.

参 考 文 献：

[1] MCGLAMERY B L.Restoration of Turbulence-degraded Images[J].Journal of the Optical Society of America,1967,57(3):293.

[2] YAN H X,LI S S,ZHANG D L,et al.Numerical Simulation of an Adaptive Optics System with Laser Propagation in the Atmosphere[J].Applied Optics,2000,39(39):3023.

[3] 蔡冬梅,王昆,贾鹏,等.功率谱反演大气湍流随机相位屏采样方法的研究[J].物理学报,2014,63(10):227.

CAI Dongmei,WANG Kun,JIA Peng,et al.Sampling Methods of Power Spectral Density Method Simulating Atmospheric Turbulence Phase Screen[J].Physics Journal,2014,63(10):227.(in Chinese)

[4] 蔡冬梅,遆培培,贾鹏,等.非均匀采样的功率谱反演大气湍流相位屏的快速模拟[J].物理学报,2015,64(22):248.

CAI Dongmei,TI Peipei,JIA Peng,et al.Fast Simulation of Atmospheric Turbulence Phase Screen Based on Non-uniform Sampling[J].Physics Journal,2015,64(22):248.(in Chinese)

[5] NOLL R J.Zernike Polynomials and Atmospheric Turbulence[J].Journal of the Optical Society of America,1976,66(3):207.

[6] RODDIER N A.Atmospheric Wavefront Simulation Using Zernike Polynomials[J].Optical Engineering,1990,29(10):1174.

[7] 王奇涛,佟首峰,徐友会.采用Zernike多项式对大气湍流相位屏的仿真和验证[J].红外与激光工程,2013,42(7):1907.

WANG Qitao,TONG Shoufeng,XU Huiyou.On Simulation and Verification of the Atmospheric Turbulent Phase Screen with Zernike Polynomials[J].Infrared and Laser Engineering,2013,42(7):1907.

(in Chinese)

[8] BAHR G V.Investigations into the Spherical and Chromatic Aberrations of the Eye and Their Influence on Its Refraction[J].Acta Ophthalmologica,1945,23(1):1.

[9] 刘良清.Matlab 辅助激光分析与应用[M].武汉:武汉凌云光电科技有限公司,2008.

LIU Liangqing.Matlab Assisted Laser Analysis and Application[M].Wuhan:Wuhan Lingyun Optoelecronic Technology Cooperation,2008.(in Chinese)

[10] 王立瑾,李强,魏宏刚,等.大气湍流随机相位屏的数值模拟和验证[J].光电工程,2007,34(3):1.

WANG Lijin,LI Qiang,WEI Honggang,et al.Numerical Simulation and Validation of Phase Screen Distorted by Atmospheric Turbulence[J].Opto-electronic Engineering,2007,34(3):1.(in Chinese)