结构光照明显微的结构光空间频率和相位测定算法

张尹馨，邓嘉俊，费建阳

(1. 光电信息教育部重点实验室(天津大学)，天津300072；2. 天津大学精密仪器与光电子工程学院，天津300072)

在生命科学研究领域，超分辨显微成像技术蓬勃发展，并且获得了超过衍射极限的成像分辨率[1-3].在这些技术中，结构光照明显微(structured illumination microscopy，SIM)因为其成像速度高、光毒性低和对荧光特性要求少等优点而得到广泛应用[4-7]．在SIM 中，使用周期性的结构光照明样品后，可以将原本位于光学传递函数(optical transfer function，OTF)支持域外的高频信息移动到OTF 支持域内，此时被移动的高频信息与低频信息混合形成混频信息．图像重建算法可分离低频和高频信息，并将高频信息移位，使之与低频信息合并形成扩展频谱．最后对拓展频谱进行傅里叶逆变换得到重建的超分辨图像[8-10]．

准确测定结构光的相位和空间频率对于分离和移动高频信息至关重要，也是重建超分辨率图像的关键[11-13]．有关空间频率和相位测定算法已有诸多报道，如迭代自相关算法(iterative auto-correlation algorithm，IAC)、迭代正弦相关算法(iterative sinusoidal correlation algorithm，ISC)[14]、峰值相位算法(phase of the peaks algorithm，POP)[15]、自相关算法(autocorrelation algorithm，AC)[16]和频谱分量互相关算法(spectral-components cross-correlation algorithm，SCC)等[17-18]．在结构光调制度较高时，这些算法均能准确计算结构光的空间频率和相位，然而并非所有SIM系统都能获得理想的结构光调制度．投影式SIM 系统[19]因其结构简单，图像采集速度快，相比结构复杂的干涉式SIM 系统[20]应用更为广泛．但是投影式 SIM 系统所生成的结构光调制度会受到物镜OTF 的影响，且随着结构光空间频率和成像深度的增加而减小．此外，当前SIM 系统逐步小型化，从实验室走向便携式应用也成为可能，光学结构由于震动产生移位会使得结构光调制度降低．因此，解决低调制度下的结构光空间频率和相位的准确测算问题不可或缺，算法不仅要保证估算精度，还要具备广泛适应性．

本文研究了前述几种结构光空间频率和相位估算算法在低调制度下的性能，分析发现SCC 算法能有效保证参数的估算精度，在不同调制度下具有较为广泛的适应性．之后进一步研究了SCC 算法，对其进行了简化．原始的SCC 算法对同一个重叠区域的相关值进行两次迭代来分别测定空间频率和相位，本文简化后的SCC 算法能够同时测定空间频率和相位．通过模拟仿真验证简化SCC 算法在低调制度下的性能，相比于其他算法，该算法可以更精确地测定空间频率和相位．实验上，利用自建SIM 系统对牛肺动脉内皮细胞(bovine pulmonary artery endothelial cells，BPAE)成像，使用简化SCC 算法测定了结构光的空间频率和相位，以此为基础重建的图像更为清晰，有效抑制了重建图像的伪影．

1 SIM的成像原理

在SIM 中，通常使用余弦形式的结构光照明样本，余弦结构光可以表示为

式中：r 为空间坐标；pd、φ、I0、m 分别为结构光的空间频率、初始相位、平均强度和调制度；下标d 表示结构光条纹的方向．

SIM 系统观测到的样本图像可以表示为

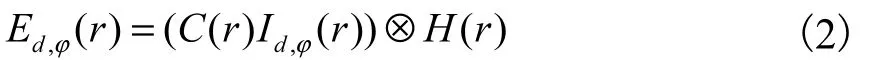
样本的荧光分子浓度 C ( r )与结构光Id,φ( r )的乘积，再卷积光学系统的点扩散函数(point spread function，PSF) H ( r )，即为SIM 原始图像Ed,φ(r)．原理如图1 所示，所得到的SIM 原始图像如图1(b)、(c)、(d)所示．

对式(2)执行傅里叶变换，可以得到SIM 原始图像的频谱表达式为

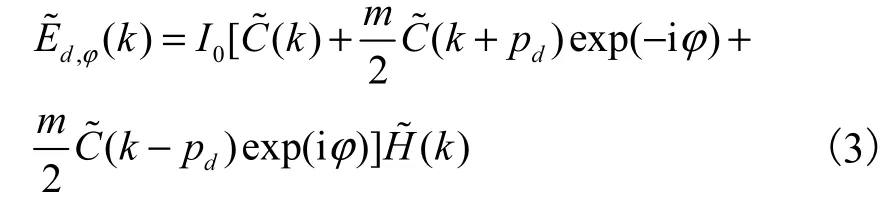
在求解出低频和高频分量之后，需要对频谱分量进行维纳滤波[14]，即

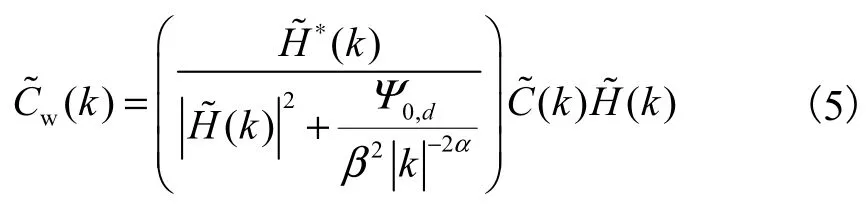
式中：上标* 代表复共轭；Ψ0,d、Ψa,d和Ψb,d是的平均噪声功率，通过和位于OTF 截止频率外频谱幅度的平方均值来估算[14]；α和β为常数，使用迭代非线性回归的方法计算[15]．滤波后的频谱分量如图1(e)、(g)、(i)所示．

图1 SIM原理示意Fig.1 Schematic diagram of structured illumination microscopy(SIM)

滤波后再对高频分量进行移位，使用傅里叶移位定理将高频分量移回到原来的空间位置[14]．如图1(f)、(h)、(j)所示．移位之后，根据式(7)将所有的频谱分量通过广义维纳滤波进行叠加，得到扩展的超分辨图像频谱，如图1(k)所示．

式中：A ( k) 为切趾函数；w 为维纳滤波常数．通过对执行傅里叶逆变换可获得重建的超分辨图像．

2 空间频率和相位测定算法原理

Lal 等[14]提出了IAC 和ISC 算法分别测定结构光的空间频率和相位．IAC 算法原理为

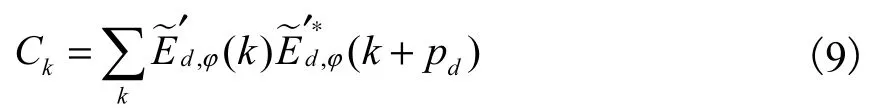
ISC 算法的原理为

式中 I1(r)=－cos(2πpdr+φ0)，φ0是一个估计的初始相位．通过迭代变换相位 φ0，并根据式(10)计算 I1( r)与SIM 原始图像Ed,φ(r)的相关值，直到迭代求出最大的相关值Cφ，此时的相位 φ0认为是准确值．但是，如果结构光调制度较低，很难将余弦函数 I1( r )与Ed,φ(r)上的结构光条纹进行准确匹配，从而产生误差.

Shroff 等[15]提出 POP 算法测定结构光的相位．根据式(3)，当k = pd时，式(3)变为

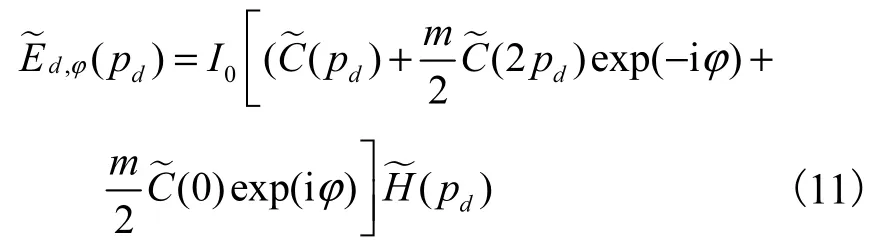
当SIM 原始图像的信噪比较高，结构光的调制度较高，空间频率适中且物频谱的高频信息衰减得足够快时，式(11)可以近似为

Wicker[16]也提出AC 算法测定结构光的相位.AC 算法的原理与IAC 算法和POP 算法原理较为相似．首先根据式(9)计算出自相关值Ck，然后根据POP 算法的近似条件对 Ck进行近似处理，可以计算出结构光的相位为

对于AC 与POP 算法，当结构光调制度较低时，无法很好地满足近似条件，此时计算结果存在误差．

3 简化频谱分量互相关算法

式中c 为白噪声的标准偏差．算法的思路如下：如果已知准确的空间频率和相位，那么就可以准确地分离出低频分量和高频分量，并能将高频分量移动到正确的空间位置上，由于重叠区域频谱信息的相似性，其互相关值较高；如果空间频率和相位不准确，那么低频与高频分量就无法准确地分离，高频分量也无法准确地移动，此时重叠区域的互相关值较低．可以利用这种性质，迭代计算出空间频率和相位．

Gustafsson 等[18]提出的SCC 算法通过迭代优化重叠区域的相关值来计算空间频率，而Wicker 等[17]使用的SCC 算法也是优化同样的重叠区域计算相位．本文的研究发现，两者是通过优化相同的重叠区域来计算不同的参数．因此，SCC 算法可以简化合并，使其能够同时计算空间频率和相位．

简化后SCC 算法流程如图2 所示．首先，设定空间频率的迭代初始值pd和相位初始值1φ 、2φ 、3φ ．然后，根据式(4)分别求出低频分量和高频分量，并利用傅里叶移位定理将高频分量进行移位．接下来根据式(14)计算重叠区域的互相关值．之后将计算出的相关值取负，将相关值和迭代的初始点代入Matlab 函数fminsearch 中，对空间频率和相位进行迭代优化[21]，当－为极小值时，所对应的空间频率和相位就是准确值．该过程可用式(16)表示．函数fminsearch 的搜索原理是基于Nelder-Mead 的单纯形算法，其具体原理可参考文献[21]．

图2 简化SCC算法流程Fig.2 Flow chart of simplified spectral-component crosscorrelation(SCC) algorithm

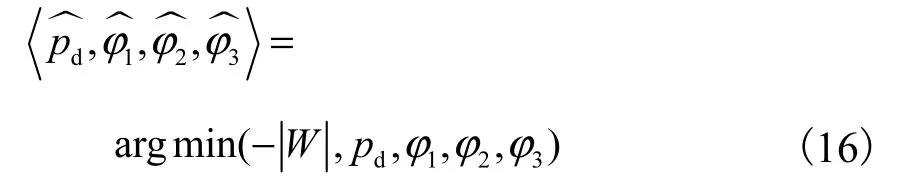
图1(k)中包括两个重叠的区域，但是这两个重叠的区域所包含的信息在数学上是相同的，所以只需要计算任意一个重叠区域的互相关值即可．关于迭代初始点的选择，可以将实验中直接测定的空间频率和相位值作为迭代的初始点．上述是0°方向结构光条纹的空间频率和相位的计算方法，其他条纹方向的计算方法与之相同．

简化的SCC 算法是一种迭代的算法，不存在近似的过程，所以理论上迭代出的空间频率和相位值即为准确值．而且简化SCC 算法是对分离后的频谱分量的重叠区域计算相关值，相比于IAC 算法，其避免了其他频谱分量对相关值产生影响，所以在低调制度下也能保持准确的结果．

在测定出结构光的空间频率和相位之后，还可以利用重叠区域内的频谱信息来测定结构光的调制度m[20]，其计算式为

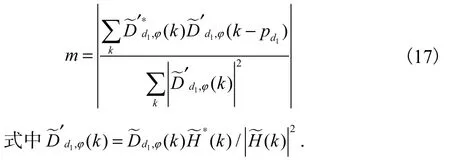
4 仿 真

通过仿真对算法进行验证．仿真条件如下：结构光的空间频率为(165 nm)－1，样本空间的像素尺寸设定为30 nm，激发波长488 nm，发射波长512 nm，物镜的数值孔径为1.49，结构光条纹的方向分别为0°、60°和120°，结构光的理想相位分别为0、2 π /3和4 π /3，并且给相位引入了一个随机的误差．

在不同的结构光调制度下，模拟不同的空间频率和相位测定算法的计算结果．结构光调制度的范围设定为0.01～1.00．为了分析噪声的影响，给SIM 的原始图像添加高斯噪声和泊松噪声．高斯噪声的方差为0.001．对于泊松噪声，使图像中最亮的像素总计为1 000 个预期的光子，作为所有单个SIM 原始图像的总和．在空间频率的估算仿真上，将简化的SCC算法与IAC 算法的结果进行比较，结果如图3 所示．

由于结构光的空间频率为矢量，通过分别计算空间频率的长度误差和方向误差来表征空间频率误差．对于简化的SCC 算法，在所讨论的调制度范围内空间频率的长度误差均低于0.065%，空间频率的方向误差低于0.02°．而对于IAC 算法，当调制度为0.18 时，空间频率的长度误差分别为0.64%(无噪声)、1.37%(泊松噪声)和1.82%(高斯噪声)．空间频率的相位误差分别为0.024 5°(无噪声)、0.072 7°(泊松噪声)和0.226 3°(高斯噪声)．当调制度低于0.18时，IAC 算法的空间频率误差还会继续增大．当调制度大于0.18 时，这两种算法的空间频率误差都很小．所以，简化的SCC 算法在低调制度下有更准确的计算结果．

在相位的估算上，将简化的SCC 算法、AC 算法和ISC 算法的相位误差进行比较，仿真结果如图4所示．简化后的SCC 算法可以同时计算结构光的空间频率和相位．但是AC 算法和ISC 算法需要提前知道空间频率才能够计算相位．在后面的讨论中，AC算法和ISC 算法使用IAC 算法所计算出来的空间频率去计算相位．

在图4 中，简化的SCC 算法在无噪声且调制度低于0.03 时相位误差低于5°，当调制度大于0.03时，相位误差低于2.5°．如果存在泊松噪声，该算法在调制度低于0.04 时相位误差接近5°，当调制度大于0.04 时，相位误差稍大于2.5°．假设存在高斯噪声，在调制度低于0.07 时，该算法的相位误差大于5°，当调制度大于0.07 时，其相位误差低于5°，并随着调制度增大而逐渐减小．对于AC 算法和ISC 算法，当调制度低于0.18 时，由于IAC 算法存在误差，因此AC 和ISC 算法也受其影响存在较大的误差．当调制度大于0.18 时，虽然IAC 算法的空间频率误差已经很小，但是受到噪声和调制度的影响，AC 算法和ISC 算法的相位误差仍然大于简化SCC 算法．所以，在整个调制度范围内，简化SCC 算法的相位误差更小．

为了获得较高的分辨率，结构光的空间频率设定约为96.7%的OTF 截止频率．有学者证明，当结构光的空间频率很高时，POP 算法会失效[17]．因此，文中没有讨论POP 算法的相位误差．

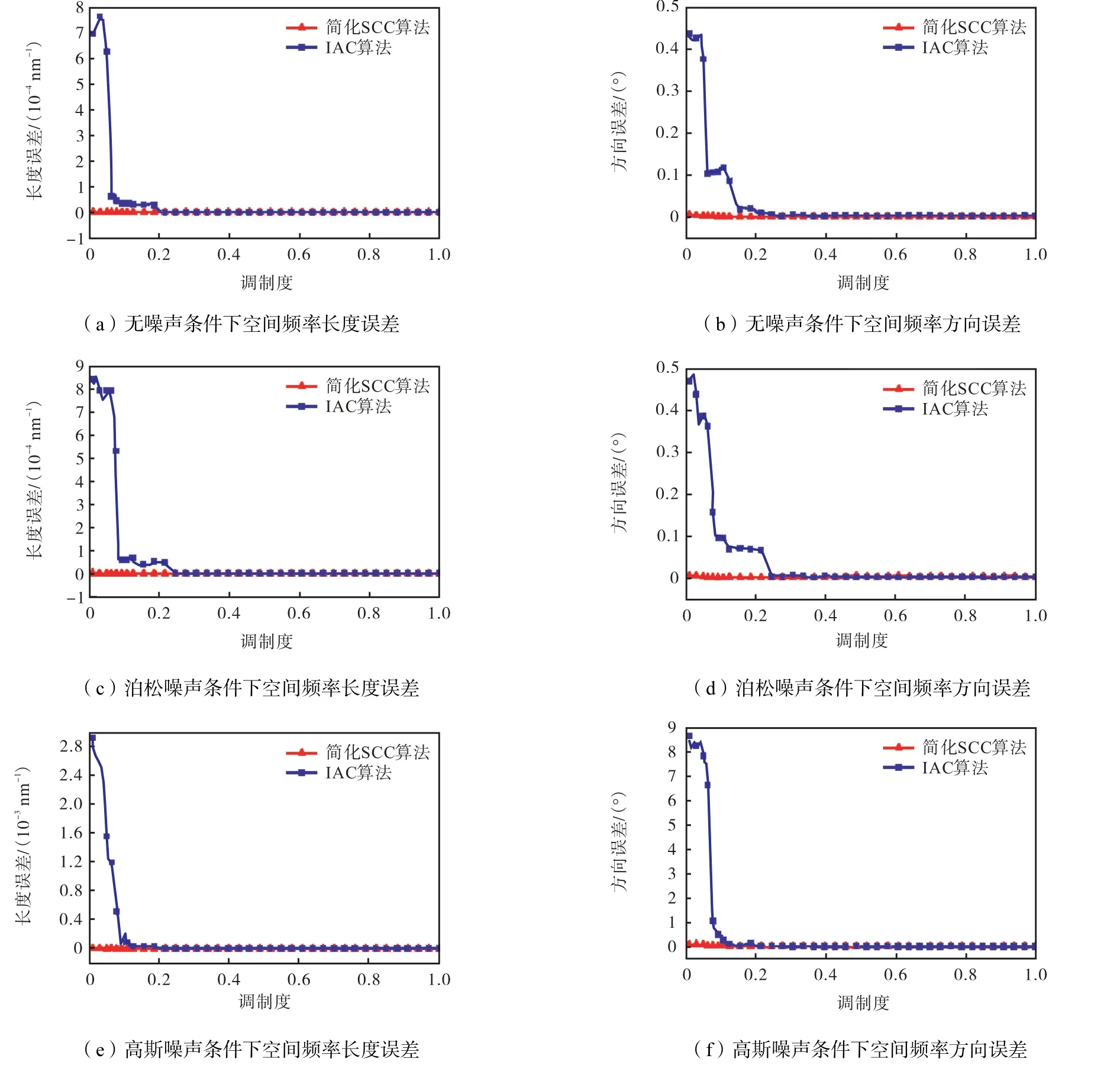
图3 在不同的调制度和噪声水平下，简化SCC算法与IAC算法的空间频率长度与方向误差Fig.3 Simulation of the magnitude and direction errors of the spatial frequencies of simplified spectral-component crosscorrelation(SCC)and IAC algorithms at different modulation depths and SNRs

在使用不同的算法计算出空间频率和相位后，利用所计算出的空间频率和相位值来重建超分辨图像，结果如图5 所示．图5(a)是仿真时使用的样本图像，图5(b)是反卷积宽场图像，图5(c)～(k)是使用了不同的空间频率和相位测定算法并结合式(4)～(8)在不同的调制度下所重建的图像．可以看到，当调制度为0.12 时，使用IAC、ISC 算法(图5(f))和IAC、AC算法(图5(i))重建的图像存在很大的误差，而简化的SCC 算法可以成功地重建超分辨图像(图5(c))．当调制度为0.18 时，使用简化SCC 算法重建的图像(图5(d))比使用IAC、ISC 算法和IAC、AC 算法(图5(g)和图5(j))重建的图像质量更好．当调制度为0.80 时，上述算法均能获得良好的重建效果．

为了定量地比较使用不同的算法在不同的调制度下所重建的图像的质量，对重建图像的峰值信噪比(peak-signal-to-noise ratio，PSNR)进行计算．计算结果如表1 所示．

图4 在不同的调制度和噪声水平下，简化SCC 算法、AC算法和ISC算法的相位误差Fig. 4 Phase errors of the simplified spectral-component cross-correlation(SCC)，AC，and ISC algorithms at different modulation depths and SNRs

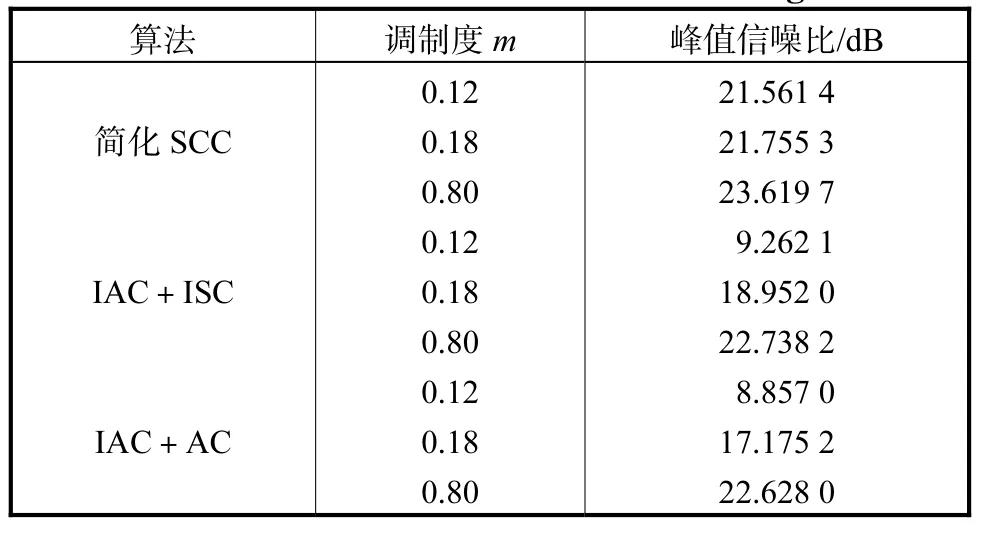
表1 重建图像的峰值信噪比Tab.1 PSNRs of the reconstructed images

PSNR 的值越大，说明重建图像的质量越好．首先分析结构光调制度对重建图像质量的影响．当结构光调制度为0.80 时，无论使用哪种算法，其重建图像的PSNR 均最大．所以随着结构光调制度的增加，重建图像的质量也逐渐提升．对于不同的算法而言，在不同的结构光调制度下，简化SCC 算法重建的图像PSNR 比其他算法重建的图像PSNR 更大，这说明简化SCC 算法重建的图像的质量更好．所以由表1 可知，无论结构光调制度高或低，使用简化的SCC 算法所计算的结构光空间频率和相位所重建的图像质量均优于以其他算法为基础的重建图像．

图5 图像重建仿真Fig.5 Simulations of reconstructed images

5 实 验

在自建的 SIM 系统上对牛肺动脉内皮细胞(bovine pulmonary artery endothelial cells，BPAE)成像，检验简化SCC 算法在超分辨图像重建上的效果.SIM 系统所使用的物镜是 Nikon CFI APOTRIF 100XH，数值孔径1.49．显微镜主体的中间放大倍率为1.5 倍，总的放大倍率为150 倍．显微镜的探测器是灵敏的sCOMS(Andor Zyla 4.2 Plus)，像素尺寸为6.5 μm. 样品是三色染色的 BPAE 细胞，用MitoTracker®Red CMXRos 标记线粒体，蓝色荧光DNA 染料DAPI 标记细胞核，Alexa Fluor 488 鬼笔环肽标记F-肌动蛋白．激发波长488 nm，发射波长512 nm．结构光的调制度约为0.17．在重建图像之前，需要对原始图像进行预处理．首先，通过Matlab函数 adapthisteq 来提高原始图像的局部对比度．然后，选择其中一张原始图像作为参考基准，调整其他原始图像的强度直方图与参考图像的直方图匹配，可使用Matlab 函数imhistmatch 来进行[12]．

用不同算法计算出的空间频率和相位所重建的图像如图6 所示．在结构光调制度为0.17 时，使用简化SCC 算法所计算出的空间频率和相位重建的图像(图6(b))明显优于以其他算法为前提的重建图像(图6(c)和(d))．与反卷积后的宽场图像(图6(a))相比，图6(b)中重建图像呈现的结构更为精细，如白色箭头标注的位置能清晰展现3 个分支，而反卷积宽场图像则无法分辨．此处的归一化强度曲线如图6(e)所示，重建图像的分辨率明显提升．实验结果表明，简化SCC 算法在低调制度下有助于更清晰地重建超分辨图像．

图6 实验图像重建结果比较Fig.6 Comparison of the experimentally reconstructed images

6 结 语

本文研究了结构光在低调制度下空间频率和相位的测定算法，通过对多种算法的分析和对比发现SCC 算法能在不同调制度下具有更广泛的适应性，精确地测算相关参数．文中对SCC 算法做了进一步研究，通过合并空间频率和相位的迭代过程实现了SCC 算法的简化，简化后的SCC 算法可以同时精确地测定空间频率和相位．仿真结果表明，该算法在结构光调制度较低时仍能准确地计算参数，相比于其他算法，其空间频率和相位误差更小．在自建的SIM 系统中对BPAE 细胞样本成像，在低调制度下，用简化的SCC 算法测定空间频率和相位，更为清晰地重建了BPAE 细胞图像，分辨率明显提升，并抑制了重建图像的伪影．简化的SCC 算法能适应不同SIM 系统对结构光空间频率和相位精确测定的需求，也能提高SIM 系统的鲁棒性．