基于稀疏贝叶斯的多跳频信号二维波达方向估计
2020-05-07李红光苏令华
李红光,郭 英,眭 萍,蔡 斌, 2,苏令华
(1. 空军工程大学 信息与导航学院, 西安 710077; 2. 北京信息技术研究所, 北京 10094)
跳频(FH)通信作为一种重要的扩频通信类型,在军事通信系统中得到了广泛应用[1-3].FH信号的空域信息是一项重要参数,能够为FH通信网台分选和干扰引导等任务提供重要依据.Lin等[4]通过构造空时频矩阵,实现FH信号波达方向(DOA)估计,但该类算法需要满足信源数小于阵元数的超定条件,在实际应用过程中受限.陈利虎[5]将空时频分析与多重信号分类(MUSIC)算法相结合,实现了FH信号在超定和欠定条件下的DOA估计,但是该算法复杂度较高.张东伟等[6]通过建立FH信号的极化敏感阵列观察模型,结合空时频分布矩阵和多项式求根方法实现DOA估计,该类算法的计算复杂度较低,但对接收阵列结构要求较为严格.Fu等[7-8]利用盲源分离的方法进行单源点检测,根据估计出的载频信息和混合矩阵实现FH信号的DOA估计,能够实现欠定条件下的多跳频信号DOA估计,但该算法只适用于正交组网方式的FH通信,在低信噪比条件下,单源点检测容易受到噪声干扰,算法鲁棒性较差.上述算法均只能完成一维DOA估计,而对于FH网台的分选和定位,二维DOA的信息特征辨识度更高.现有文献对于FH信号的二维DOA估计较少,于欣永等[9]首先构造每一跳信号的空时频矩阵,将共轭子空间的思想引入到MUSIC算法中,通过半普搜索实现多跳频信号的二维DOA估计,该算法在一定程度上降低了MUSIC的计算复杂度,但只适用于不相关信源.张东伟等[10-11]通过设计阵元时频点选取策略,构建了每跳信号空间极化时频矩阵,并利用最小二乘旋转不变子空间(ESPRIT)算法完成多跳信号的二维DOA估计,但该算法必须预先知道信源个数,运算量较大.
随着压缩感知技术不断发展,基于稀疏重构理论的DOA估计算法[12-13]相继出现,这类算法不易受信源数量和相干性的影响,对接收天线阵列误差和噪声敏感度低.目前,基于压缩感知的DOA算法主要应用于非FH信源.韩树楠等[14]对近似0范数稀疏类算法进行改进,利用奇异值分解估计出DOA,提高了算法在低信噪比、低快拍数条件下的DOA估计性能.但是,该算法在求解凸优化问题的过程中计算复杂度较高,而且容易受空间谱伪峰和正则化参数变化的影响,导致DOA估计不准.Lei等[15-16]采用稀疏贝叶斯学习(SBL)方法完成了DOA估计,此类算法保持了L1范数稀疏重构算法的估计性能,具有更强的可拓展性,计算复杂度也有所降低.
为了实现对FH信号二维DOA估计,更好地辅助于FH信号网台分选,本文利用L型阵列的结构特点,将FH信号方位向和俯仰向的二维DOA估计问题转化为两个一维DOA估计问题,再构建空间频率的过完备字典,通过SBL重构方法求得方位向和俯仰向的空间频率,再由Capon[17-18]空间频率配对算法完成FH信号频率和空间频率的正确配对,最终解算出FH信号跳频率、方位角和俯仰角三维信息.为了降低算法计算复杂度,利用奇异值分解方法对两个子阵的接收矩阵进行降维预处理,降低矩阵维数,减少运算时间.
1 数学模型
1.1 FH信号L型阵列接收模型
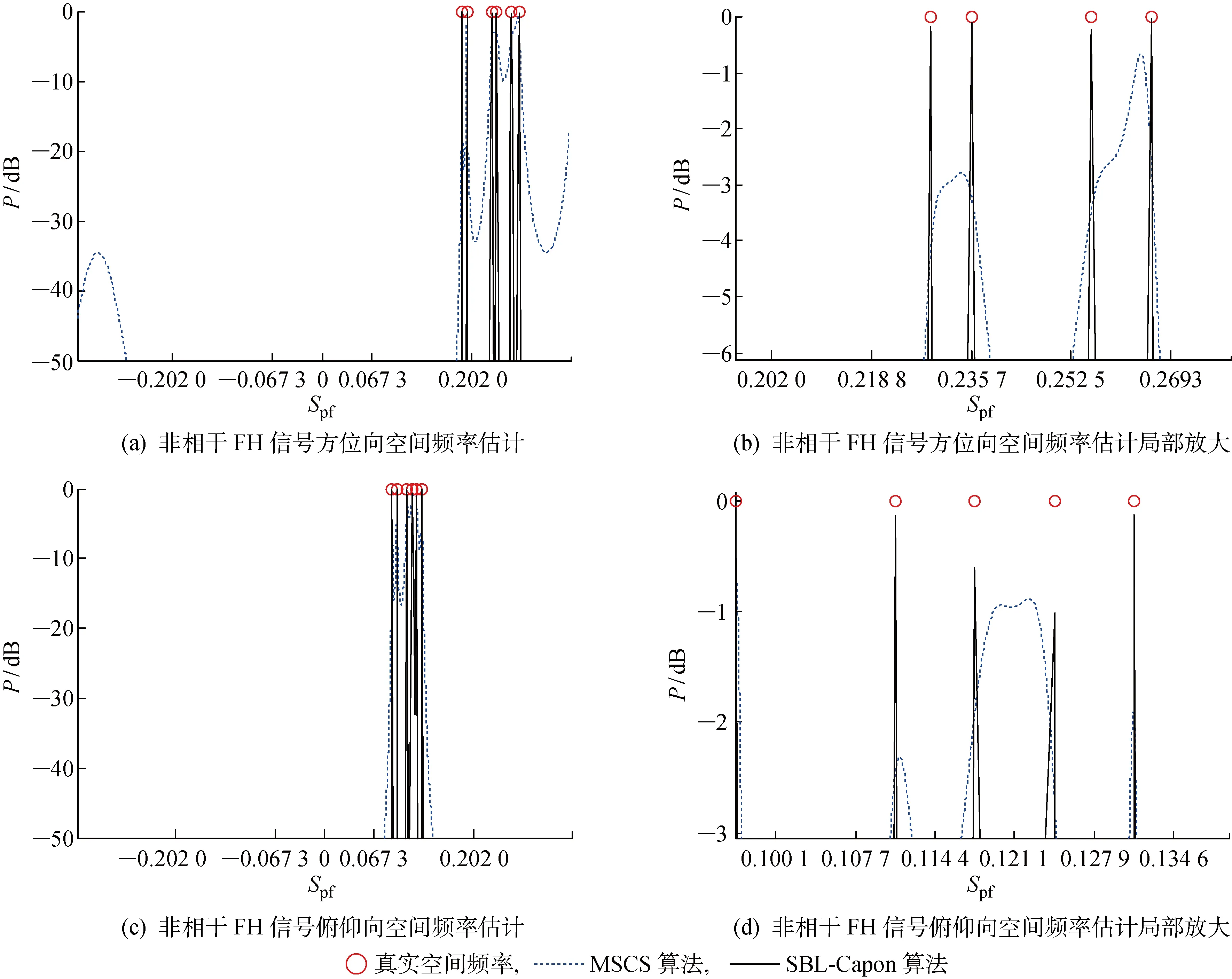
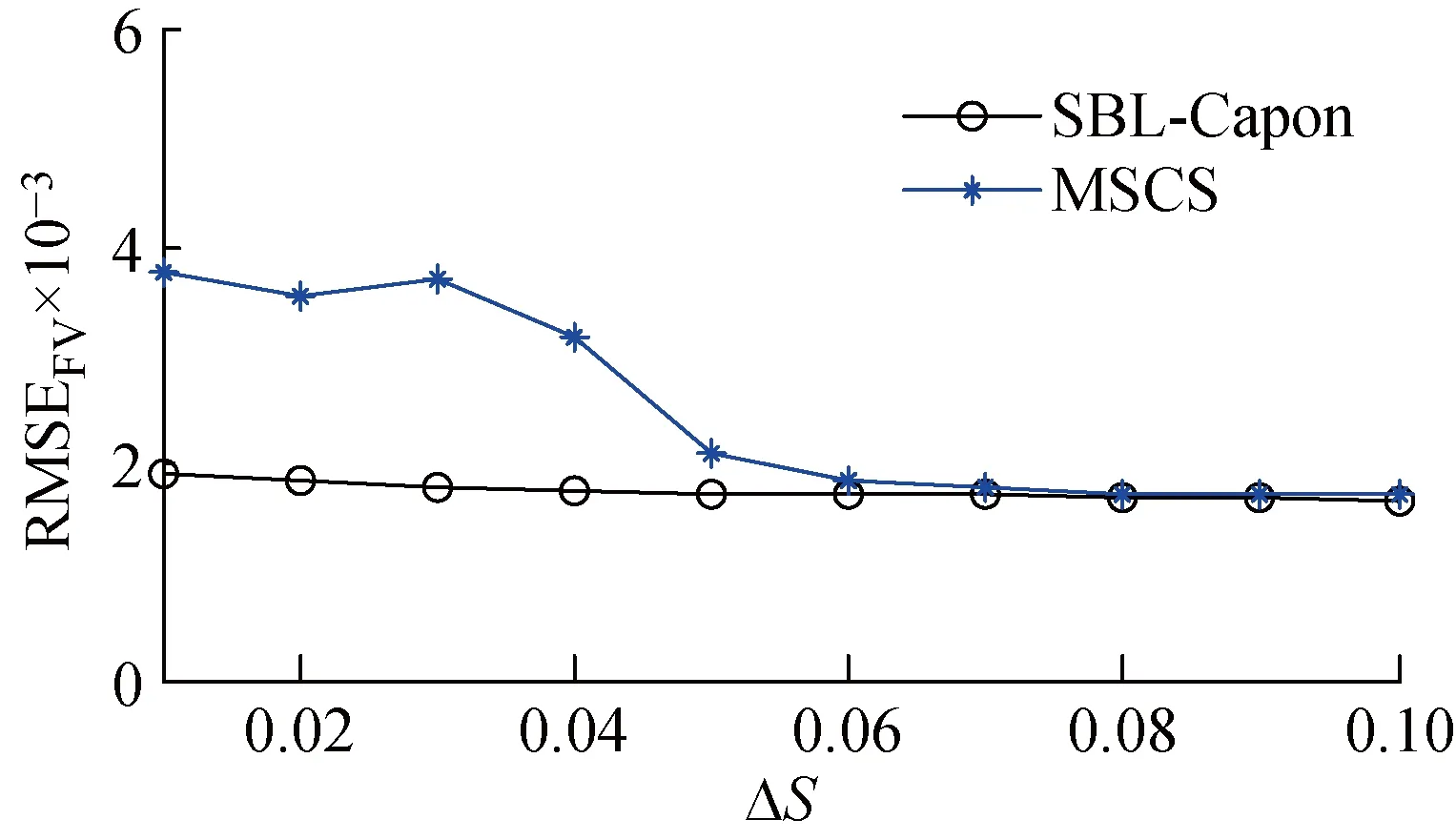
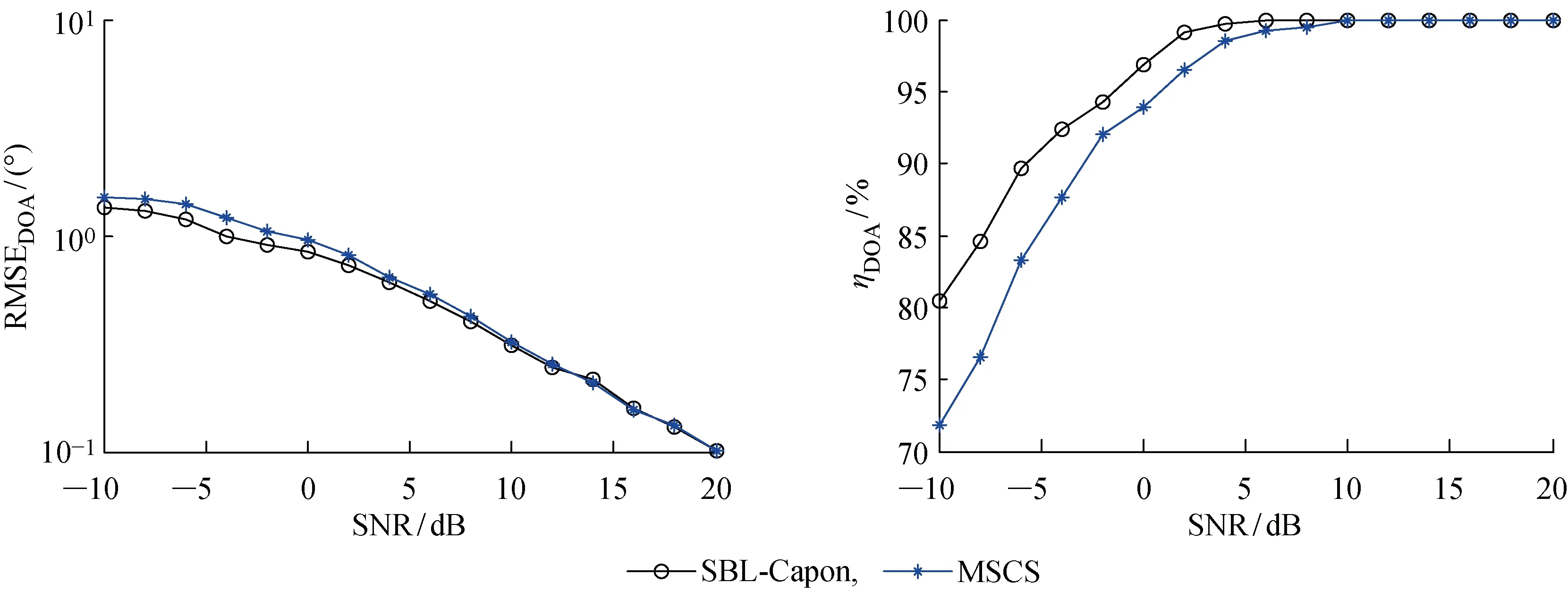
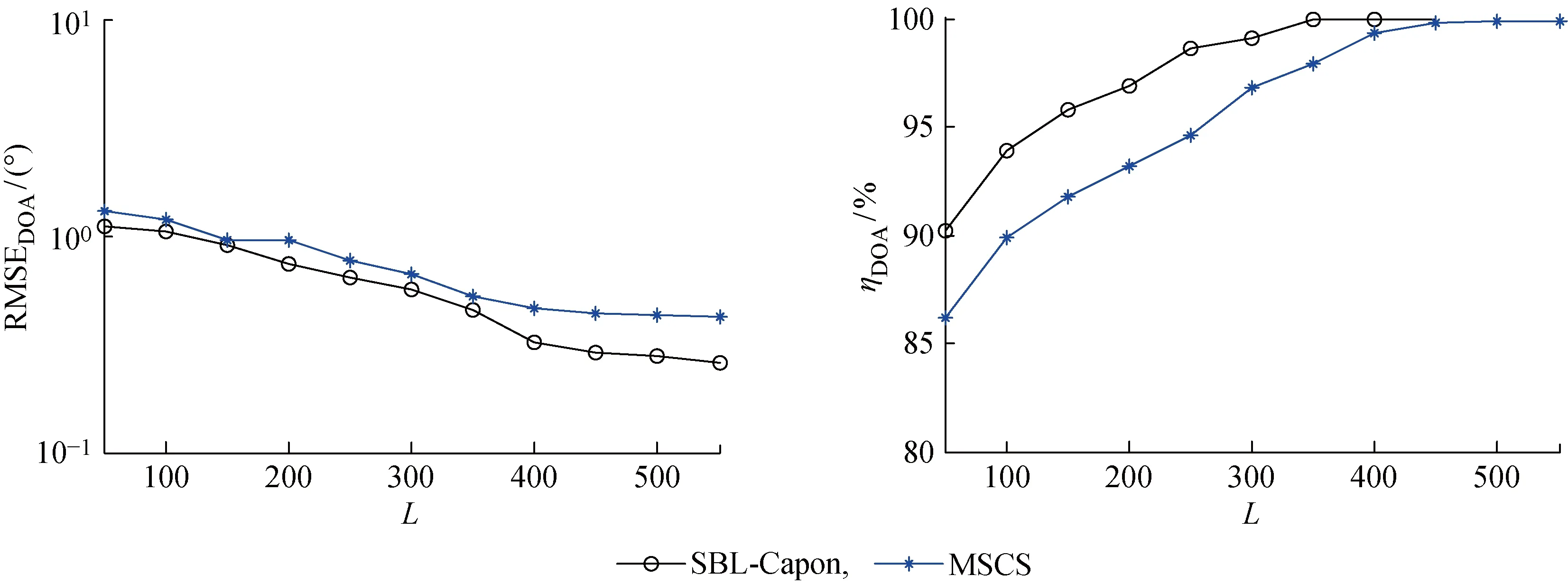
假设有K个远场FH信号s(t)=[s1(t)s2(t) …sK(t)]T入射到一个L型阵列,如图1所示,图中αi和βi分别为FH信号si(t) (i=1,2,…,K)入射方向与子阵x及y的夹角.该L型阵列位于x-y平面,子阵x和y互成90°,每个子阵分别由M(M>K)个阵元组成,阵元间距均为d且d 图1 FH信号L型阵列接收示意图Fig.1 Schematic diagram of FH signal L-array reception 在观测时间内,第i个FH信号可表示为 (1) 式中:νi为si(t)的幅度;Bi为在观测时间内si(t)的总跳数;fi,bi为si(t)第bi跳的载频;Ti为si(t)的跳频周期;t′为观测时长,t′=t-(bi-1)Ti. 假设接收阵列中各阵元是各向同性的,则第i个FH信号在子阵x和y的导向矢量分别为 (2) (3) 式中:τi,m=(M-m)fi,bidcosθisinφi/c;υi,m=(M-m)fi,bidsinθisinφi/c,m=1,2,…,M. 由图1所示的空间几何关系可得 将式(4),(5)代入式(2),(3)得 (6) (7) 由式(6)和(7)可知,FH信号在子阵x和y的方位角、俯仰角和跳频率三维信息可由空间角和跳频率二维信息表示.为了进一步降低算法求解难度,现定义第i个FH信号在频率fi,b处的方位向空间频率为Hi,b,俯仰向空间频率为Vi,b,其表达式为 由式(8)和(9)可知,子阵x和y的导向矢量为 (10) (11) 由式(10)和(11)可知,FH信号在子阵x和y只有空间频率一维信息,则接收阵列流型矩阵可分别表示为 (12) (13) 从而得到子阵x和y接收的FH信号分别为 考虑到子阵x和y接收的FH信号空间频率具有稀疏性,分别将方位向空间频率和俯仰向空间频率进行均匀离散划分,得到超完备的空间频率集合,分别为F={F1,F2,…,FN}和G={G1,G2,…,GN},Fn和Gn分别表示空间频率集合F和G中的第n个空间频率元素,n=1,2,…,N,N为划分网格数且N≫M>K.则由式(14)和(15)可得基于空间频率的子阵x和y单测量阵列输出模型: 在多快拍数条件下,将子阵x和y每次接收的快拍数据L作为1个快拍帧进行运算,则基于空间频率的稀疏表示为 (20) 同理,对于子阵y接收的FH信号也可以估计出其俯仰向空间频率,即 (21) 在实际应用过程中,为了提高FH信号DOA的估计精度,一般需要增加FH信号的快拍数L,但是随着快拍数L的增加,输出矩阵的维数增多,这必然会导致计算量大幅增加,算法的时效性降低.为了在保证算法估计精度的基础上减少算法运算时间,采用奇异值分解(SVD)的方法分别对输出矩阵X和Y进行降维处理.根据文献[19-20],矩阵X和Y的SVD表达式为 式中:Ux和Uy分别为X和Y的M×M维左特征正交矩阵;Σx和Σy为M×L维对角阵;Wx=[Wx1Wx2]和Wy=[Wy1Wy2]分别为X和Y的L×L维右特征正交矩阵,Wx1和Wy1分别为Wx和Wy的前K列.Wx1和Wy1中分别包含了X和Y经过SVD分解后的特征值所对应的所有特征向量,因此可得X和Y经SVD降维后的矩阵Xsvd和Ysvd分别为 Xsvd和Ysvd包含了子阵x和y接收的所有FH信号空间频率信息,可将式(18)和(19)转化为 本节利用SVD算法将M×L维输出矩阵X和Y降低到M×K维,且SVD算法本身对子阵接收的噪声产生抑制作用.由于噪声的奇异值相对于FH信号非常小,所以在SVD过程中能够将FH信号中的大部分噪声分离出来,提高了算法在低信噪比条件下的估计性能. 本节以子阵x为例,求解方位向空间频率.根据式(26),其观测噪声矩阵Ex-svd各列均是相互独立的,且服从均值为0,协方差矩阵为(σ2/L)IM(IM为M×M维单位矩阵)的高斯分布.则Xsvd关于FH信号幅度的概率密度函数可表示为 (28) 本节SBL引入中间参数γ=[γ1γ2…γN]T表示FH信号在空间频率集Dx上的功率谱分布,各参数间相互独立,且有 (29) 式中:N(0,Γ)为均值为0,协方差矩阵为Γ的高斯分布,Γ=diag(γ). (30) (31) (32) 式中:US为均值;ΣS为方差. 对式(30)取对数并忽略其常数项,即可得到优化γ的目标函数: (γ, (33) (34) 通过式(34)的j次迭代运算后,可估计出所有FH信号的方位向空间频率集 则其对应噪声功率的无偏估计值为 (35) (36) 式中:λm表示Xsvd的第m个奇异值. 根据式(8),其方位向空间角可表示为 αi=arccos(cHi,b/fi,b) (37) 可见,只要将FH信号的跳频率和空间频率正确配对,即可估计出方位向和俯仰向的空间角,从而解算出方位角、俯仰角和跳频率三维信息. 将式(14)进行傅里叶变换,可得到子阵x接收的混合信号在fi,b处的频域输出为 x(fi,b)=Ax(Hi,b)sx(fi,b)+ex(fi,b) (38) 式中:sx(fi,b)为子阵x接收的FH信号在fi,b处的频域输出;ex(fi,b)为子阵x接收的噪声在fi,b处的频域输出. 根据Capon波束形成思想,对方位向空间频率上的FH信号功率进行归一化处理,并最小化子阵x输出功率,其约束方程为 (39) 式中:ω为最优权值系数,根据文献[24]有 (40) Rx(fi,b)为频率fi,b处的频域协方差矩阵, Rx(fi,b)=E[x(fi,b)xH(fi,b)] (41) (42) (43) (44) (45) (46) 本文算法的具体步骤如下: (1) 构造方位向和俯仰向空间频率字典F和G. (2) 根据式(18)和(19)构造方位向和俯仰向空间频率的阵列输出矩阵X和Y,流型矩阵Dx和Dy. (3) 根据式(24)和(25)降低输出矩阵X和Y经过SVD分解得到降维后的矩阵Xsvd和Ysvd,减少计算量. τ= (47) 图2 相干FH信号的空间频率估计和空间角与频率配对结果Fig.2 Spatial frequency estimation and pairing results of coherent FH signals 本节通过实验验证,对比分析本文算法和文献[13]基于MUSIC的对称压缩谱算法(MSCS)的二维DOA估计性能.假设有若干个远场FH信号分别从不同角度入射到L型均匀阵列上,子阵阵元数均为8,阵元间距为1 m,角度范围 -90°~90°,频率范围0~100 MHz,则空间频率Hi,b和Vi,b的范围为 -0.333 3~0.333 3,超完备字典网格数N=400. 实验1验证本文算法对相干FH信号的空间频率估计以及与跳频率正确配对的有效性.假设两个远场相干FH信号的入射角分别为(-25°,57°)和(33°,-48°),FH周期均为100 μs,频率集均为{41,62,87} MHz,采样率为200 MHz,采样时长为1 ms,信噪比为0.经计算,两个FH信号的空间频率分别为(0.103 9,-0.048 4),(0.157 1,-0.073 3),(0.220 4,-0.102 8)和(-0.085 2,-0.055 3),(-0.128 8,-0.083 6),(-0.180 7,-0.117 4).图2所示为两个相干FH信号在快拍数为80条件下的空间频率估计和配对结果.图中:P为功率;Spf为空间频率;Spa为空间角.从图2(a)和2(b)可知,SBL-Capon算法能够实现对相干FH信号空间频率的有效估计.从图2(c)和2(d)可知,在完成空间频率正确估计后,利用基于FFT变换的频率估计和Capon空间频率配对算法, 将空间频率和跳频率进行正确配对并得到空间角,根据入射角空间几何关系,计算出方位角和俯仰角,实现了FH信号跳频率和二维DOA的联合估计.由图2(c)还可以看出,SBL-Capon算法能够将FH信号频率集进行分选,即相同空间角度的跳频率来自于同一个FH信号,当观测时间足够长时,即可完成FH信号的跳频率集估计,能够有效辅助FH网台分选. 实验2对比分析SBL-Capon和 MSCS两种算法在不同空间频率间隔下的空间频率估计精度.由空间频率定义和空间角几何关系可知,空间频率的估计精度对DOA的解算精确性有重要影响.为了方便控制仿真中各FH信号间的空间频率间隔,由于MSCS算法只适用于非相干信源,所以取入射角相近的两个非相干FH信号.其入射角分别设为(25°,64°)和(27°,62°),频率集均为{71,86,97} MHz,跳周期分别为100和50 μs,采样率为200 MHz,采样时长为1 ms,信噪比0 dB,快拍数为80.经计算,两个FH信号的空间频率分别为(0.192 8,0.089 9),(0.233 5,0.108 9),(0.263 4,0.122 8)和(0.186 2,0.094 9),(0.225 5,0.114 9),(0.254 4,0.129 6).图3为SBL-Capon和 MSCS两种算法的空间频率估计结果.从图3(b)和3(d)可知,当FH信号源的空间频率间隔较小时(即空间角度相近),SBL-Capon算法的估计精度优于 MSCS算法的估计精度. 图3 非相干FH信号的空间频率估计结果Fig.3 Spatial frequency estimation results of non-coherent FH signals 图4所示为空间频率估计的方均根误差随最小空间频率间隔的变化情况,图中ΔS为最小空间频率间隔,空间频率范围为0.01~0.1,最小间隔0.02,空间频率的方均根误差为 RMSEFV= (48) 从图4可知,当两个FH信号的最小空间频率间隔较小时,SBL-Capon的空间频率估计性能优于MSCS算法的空间频率估计性能.随着空间频率间隔增加,MSCS算法的空间频率估计精度逐渐提高,SBL-Capon算法的估计性能基本保持不变,不易受空间频率间隔影响,当空间频率间隔大于0.07时,SBL-Capon和MSCS算法的估计性能基本一致. 实验3对比分析SBL-Capon和 MSCS两种算法在不同信噪比下DOA方均根误差和估计成功率.假设:3个非相干远场FH信号,入射角在 -90°~90° 范围内随机产生,角度间隔不小于2°;FH周期分别为150,100和80 μs;频率集分别为65~95 MHz范围内的3个随机频率,且同一个FH信号的相邻跳点频率间隔大于5 MHz;采样率为200 MHz,采样时长为1 ms,快拍数为80;信噪比范围 -10~20 dB,间隔为2 dB. 图4 空间频率估计的方均根误差随最小空间频率间隔变化Fig.4 Root mean square error varies of the spacial frequency with minimum spatial frequency interval DOA方均根误差RMSEDOA和估计成功率ηDOA分别为 RMSEDOA= (49) (50) 图5 不同信噪比下DOA估计性能Fig.5 DOA estimation performance under different SNR 图6 不同快拍数下DOA估计性能Fig.6 DOA estimation performance under different snapshots 图5所示为RMSEDOA和ηDOA随信噪比SNR增加的变化情况.从图5可知,随着信噪比增加,两种算法的DOA估计方均根误差逐渐减小,估计成功率逐渐提高.在低信噪比条件下,SBL-Capon算法的估计精度和成功率均高于MSCS算法.主要原因是由于SVD降维预处理和SBL稀疏求解过程都对噪声起到抑制作用,当信噪比大于10 dB时,两种算法的估计性能基本一致. 实验4对比分析SBL-Capon和 MSCS两种算法在不同快拍数下DOA方均根误差和估计成功率.假设:3个非相干远场FH信号,入射角在 -90°~90° 范围内随机产生,角度间隔不小于2°;FH周期分别为150,100和80 μs;频率集分别为 65~95 MHz范围内的3个随机频率,且同一FH信号的相邻跳点频率间隔大于5 MHz;采样率为200 MHz,采样时长为1 ms,信噪比0 dB;快拍数范围50~550,间隔50.图6所示是RMSEDOA和ηDOA随快拍数变化情况.从图6可知:随着快拍数的增加,两种算法的DOA估计性能逐渐提高;在低快拍数条件下,SBL-Capon的DOA估计精度和成功率均优于MSCS算法;当快拍数大于450后,两种算法的估计性能基本保持不变. 实验5对比分析SBL-Capon算法在不同字典网格数N下DOA方均根误差RMSEDOA和运算时间t.假设:3个非相干远场FH信号,入射角在 -90°~90° 范围内随机产生,角度间隔不小于2°;FH周期分别为150,100和80 μs;频率集分别为65~95 MHz范围内的3个随机频率,且同一FH信号的相邻跳点频率间隔大于5 MHz;采样率为200 MHz,采样时长为1 ms,快拍数为80;信噪比范围 -10~20 dB,间隔2 dB;N取值分别为300,400和500.运算时间均是在MATLAB2014环境下,通过TIC和TOC指令计算平均运算时间t. 图7所示为不同网格数N条件下RMSEDOA和t随信噪比增加的变化情况.从图7可知,在相同信噪比条件下,字典网格数越小,算法运算时间越短.这主要是由于字典网格数减少使得流型矩阵各列之间相关性减弱,从而减小了超参数求解的迭代次数,加快了算法收敛,但是DOA估计精度也有所下降.因此,在实际应用中,要根据FH信号带宽范围合理划分字典间隔. 图7 不同网格数下DOA估计性能和运算时间Fig.7 DOA estimation performance and operation time under different grid numbers 为了更好地辅助FH信号网台分选,本文提出一种基于稀疏贝叶斯学习的FH信号二维DOA估计算法.该算法首先根据入射角的空间几何关系,将方位角、俯仰角和跳频率三维信息转换为一维空间频率信息,降低了稀疏重构算法复杂度.然后经过SVD降维处理,减少矩阵运算维数,通过SBL算法估计出空间频率,利用FFT频率估计算法和Capon空间频率配对算法将空间频率和跳频率正确配对,解算出方位角和俯仰角.实验结果表明,在低信噪比或低快拍数条件下,该算法能有效估计出相干或非相干多FH信号的二维DOA信息,而且不易受空间频率间隔影响.如何进一步提高本算法时效性,以及实现FH信号DOA和极化参数的联合估计是下一步研究工作.

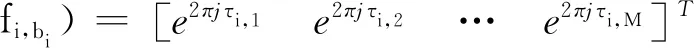


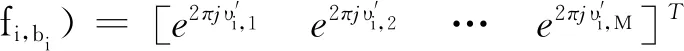
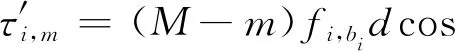

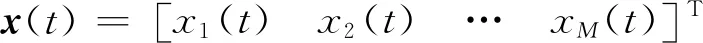
1.2 基于空间频率的FH信号稀疏表示
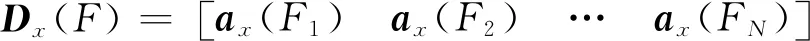

2 算法原理
2.1 输出矩阵降维预处理

2.2 基于SBL的空间频率估计



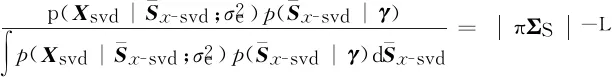


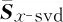
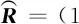
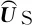


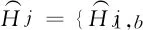

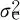

2.3 Capon空间频率配对方法
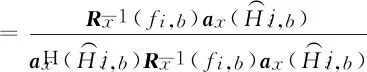



2.4 算法流程及复杂度分析





3 实验结果与分析




4 结语
