农业技术推广效率测度及影响因素研究*

赵玉姝，焦 源，高 强

(1.西安工业大学 经济管理学院，西安 710021；2.中国海洋大学 管理学院，青岛 266100)

农业技术(简称农技)推广效率是指农技推广人员完成一定量任务的基础上耗用或占用推广资源的情况.农技推广作为连接技术研发和技术采纳的中间环节，其效率的高低直接影响技术成果转化及“产学研用”四维一体发展模式的顺利运行.当前，我国农技推广体系部分呈现出“线断、网破、人散”尴尬局面，部分行政化推广方式忽视农民需求，造成农业科技成果产、学、研、用环节的相互割裂，推广效率低下.从方法论角度来看，当前学术界对农技推广效率的研究有非参数数据包络分析法(Data Envelopment Analysis，DEA)和基于参数随机前沿生产函数方法(Stochastic Frontier Approach,SFA)两类.数据包络研究有对1990-2005年间中国的农业技术推广效率分析[1]，以2005年31个省的数据，使用DEA建立优势农业技术推广效率模型并提出效率模型评价的缺点[2]，以SFA模型为基础分别对中国食品技术、工业用水和高技术产业创新进行测度[3-5].部分研究使用传统DEA模型测度相关效率问题时无法摒弃随机变量和环境因素的作用，导致实证结果难以客观反映现实状态.文中在筛选农技推广效率影响因素的基础上，以国内31个省市自治区(不含香港、澳门和台湾)相关数据为对象，利用三阶段DEA模型进行实证分析，探究影响我国农技推广效率的制约性因素，并提出相应解决措施.

1 模型方法与指标选取

1.1 模型方法

针对传统DEA模型无法消除环境变量和随机因素等非经营因素影响的缺陷，参考Fried提出三阶段 DEA 模型，旨在更好的评价决策单元的效率水平[6].三阶段DEA模型构建如下：

1) 第一阶段传统DEA模型.传统数据包络模型多用于测度“多投入多产出”条件下决策单元(Diesel Multiple-Unit，DMU)之间的相对有效性[7].采用规模报酬可变(Variable Return to Scale，VRS)假设下的BCC(Banker，Charnes and Cooper)模型测度国内农技推广效率水平，其基本原理是以推广资源不变为前提，计算农技推广的最优产出与实际产出之间距离，距离越远表征推广的效率水平越低.对于决策单元DMU,投入导向下对偶形式的 BCC模型用线性规划方程表示为

minθi

式中:i为决策单元序列号；j为输入变量序列号；r为输出变量序列号；s+，s-为输出变量的界值；i= 1,2,…,n;j= 1,2,…,m;r= 1,2,…,s;θi为决策单元的效率值；n,s和m分别表征决策单元、输出变量和输入变量的个数；xij,yir,λi分别为第i个决策单元的第j个投入要素、第r个产出要素和权重系数.通过BCC模型测度的效率值θi可继续分解成纯技术效率和规模效率的乘积，其中效率值是推广资源合理配置和使用的综合反映，纯技术效率是受技术和管理要素影响的推广效率，规模效率是受推广服务涵盖范围和规模影响的效率水平.

2) 相似SFA 分析模型.第一阶段DEA模型所得决策单元效率值及松弛变量受管理效率、环境变量和随机变量三个方面的影响，松弛变量指最优投入和实际投入的差额[8].为排除后两类外生变量对原始数据的作用，在第二阶段构建相似SFA分析模型对环境变量和随机变量进行分离，得出仅由管理无效率造成的决策单位投入冗余.假定松弛变量ski=xji-λixji，对每个DMU的投入松弛变量进行SFA分析，其模型为

ski=fk(Zi,βk)+vki+uki,k=1，2，…,K，

i=1，2，…，n

式中：Zi，βk分别为环境变量与待估参数；uki为混合误差项；vki为随机干扰；K为随机干扰数；fk(·)为环境评估误差函数.

假设vki～N(0,σ2);uki为管理无效率，假定其服从截断正态分布.σ2为方差.

利用SFA模型结果，对DMU的各项投入量做出调整.调整方法是在随机因素、农技推广环境最恶劣的基础上，将决策单元的其他投入样本向上增加，具体方程为

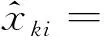
利用这一方法计算出的效率值可以准确反映DMU的内部管理情况，减少误差影响并提高计算的准确性.

1.2 变量选取与数据来源

遵循统计口径一致性和数据可得性原则，选取农业技术推广面积和农业生产总值作为计算农技推广效率的产出变量.其中农业技术推广面积是指一年农技推广人员服务覆盖及成果应用的面积统计；农业总产值是指以货币表示的农林牧渔产品及其相关服务的价值总量.投入变量选取农技推广人员数量，推广部门承担的省级以上科研项目数和推广部门获得的财政投资强度(用于农技推广活动的财政拨款占农业生产总值的比重).文中农技推广面积、省级以上推广项目数和农技推广人员数据来源于各地农业统计年鉴；农技推广人员受教育水平、农民受教育水平财政扶持强度、受灾面积和农业生产总值来源于《中国农村统计年鉴》，并经过相应整理和统计；各地国内生产总值数据摘自《中国统计年鉴》.

1) 投入及产出变量的选取及说明

利用三阶段DEA模型对农技推广效率进行测度之前，验证投入要素和产出要素的同向性关系，即投入要素的增加将至少保证产出要素不会减少[9-11].利用spss18软件，对投入要素和产出要素进行Pearson相关系数检验，计算结果见表1.可以看出，投入量和产出量之间的相关系数均能通过10%的显著性水平检验，且符合同向性特征.

2) 环境变量的选取及说明

环境变量的选取原则为对农技推广效率产生影响但不受主观意愿制约的因素[12-13].基于此，文中选择国内生产总值、农民与农技推广人员受教育水平和受灾面积3种变量进行考察与测度.① 国内生产总值.地区国内生产总值对农技推广效率的影响主要在于国民生产总值能够充分反映地区经济实力，有利于提升财政扶持水平，优化农技推广体制机制.② 农民与农技推广人员受教育水平.农民的受教育水平不但影响其对农业技术的理解，而且将在很大程度上决定农业技术的采纳意愿；农技推广人员的受教育程度与农技推广效率的关系更为密切，如果推广人员受教育程度不高，不具备良好的个人素质和沟通能力，将无法有效完成推广，农技推广效率将大打折扣.③ 受灾面积.自然灾害对农技推广效率的影响虽非常态化，但灾害的频繁发生会影响农民技术采纳，进而制约农技推广效率.

表1 2016年部分农业技术推广投入量和产出量的Pearson相关系数检验

注：*,**,***分别为变量在1%,5%和10%通过显著性水平检验，括号内的数字为检测P值.

2 实证分析

2.1 第一阶段传统DEA模型分析

基于传统DEA模型，利用deap2.1软件测度31个省市自治区农技推广效率，所得结果见表2.其中， PTE,SE,TE分别表示技术推广的纯技术效率、规模效率与综合技术效率.从表2中可看出，国内31个省市自治区尚未摒弃随机变量和环境变量情况下的3项效率值.此外，通过比较技术前沿面和实际效率值，计算出各地农技推广效率的松弛变量，为第二阶段SFA模型构建提供数据.

2016年国内31个省市自治区农技推广的综合技术效率平均值为0.828，其中东部11省市自治区,包括北京市、天津市、河北省、辽宁省、上海市、江苏省、浙江省、福建省、山东省、广东省和海南省等的平均效率值为0.932，中部8个省市自治区,包括山西省、吉林省、黑龙江省、安徽省、江西省、河南省、湖北省和湖南省等的平均效率值为0.857，西部包括四川省、重庆市、贵州省、云南省、西藏自治区、陕西省、甘肃省、青海省、宁夏自治区、新疆自治区、广西自治区和内蒙古自治区等12省市自治区的平均效率值为0.715，中部和西部有关农技推广效率与东部地区差距较为明显.从全国范围来看，山东和江苏两省的综合技术效率为1，处于技术前沿面；纯技术效率的全国平均值为0.907，规模效率的均值为0.907，两个统计数值差距不大且整体水平较好.由于环境因素和随机因素的干扰，所得结果未反映各地农业生产效率的实际水平，仍需进一步调整和测量.

2.2 第二阶段SFA模型分析

将4项环境因素作为自变量，前沿面与实际效率值之差计算出的松弛变量为因变量构建SFA模型，利用frontier4.1软件进行测度，软件处理结果见表3.

表2 2016年农技推广的综合技术效率、纯技术效率和规模效率水平

注：irs为规模效益递增；drs为规模效益递减；—为规模效益不变.

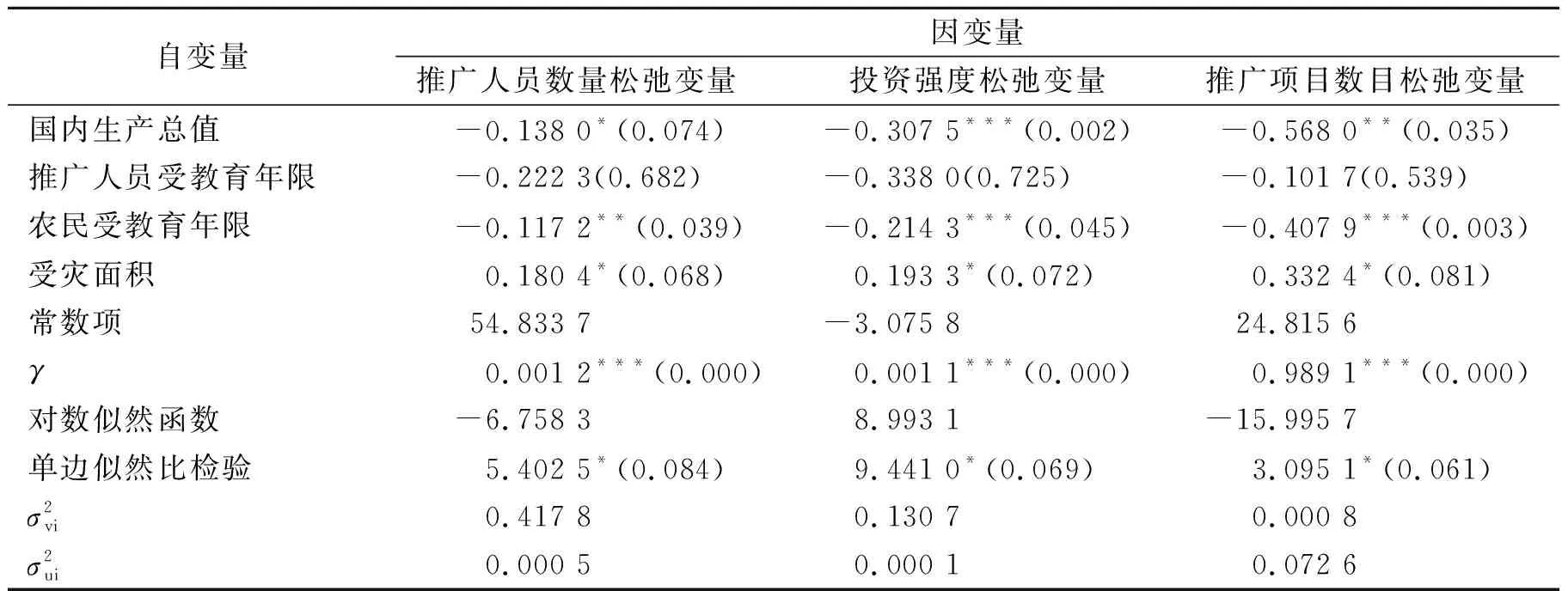
表3 SFA模型数据处理结果

从数据与模型的拟合情况来看，3个回归方程的单边似然比检验能够通过10%显著性水平检验;γ通过1%的显著性水平检验，表明数据与模型的契合度较好.具体而言，推广人员数目和投资强度松弛变量的γ值为0.001 2和0.001 1，表征随机误差对两种松弛变量的影响占主导地位；推广项目数目松弛变量的γ值是0.989 1，说明管理因素对该松弛变量产生较大影响.此外，四项环境变量在推广人员数量、投资强度和推广项目数模型中的回归系数分别通过1%,5%和10%的显著性水平检验，可以判断环境变量在不同程度上影响松弛变量的大小与方向.

国内生产总值变量在3个回归方程中的系数同为负值，说明随着各省、市和自治区国内生产总值的增长松弛变量数值不断下降，农技推广效率随之上升.国内生产总值与农技推广效率同步增长的原因包含两个方面：首先，经济增长有利于优化农业生产环境和相应配套设施，化解因投资不足而导致的农技推广形式单一、内容落后的尴尬困境[14].其次，国内生产总值的增加为提高基层农技推广人员待遇提供物质基础，进而激发推广人员服务热情,提升技术推广效率.

从回归系数角度来看，推广人员受教育水平在3个回归方程中的系数为负值，表明推广人员受教育程度与农业技术推广效率值呈正相关.这一变量均未通过10%的显著性水平检验，高学历推广人员对农技推广效率提升的作用很不明显.其原因主要在于受职称评审、升迁和工作环境等综合影响，高学历人员多承担行政与科研任务，从事基层农技推广工作的可能性较低[15].此外，获取学历过程中的知识储备同现实农业生产服务存在差距，推广人员眼高手低的情况较为普遍.

农民受教育水平在3个回归方程中的系数同

为负值，且通过1%的显著性水平检验，表征随着农民受教育程度的增长松弛变量数值不断下降，农技推广效率提升明显.农民受教育程度越高，对农业技术的需求及采纳意愿越明显，这种技术需求将引发农民自主性学习动力，在提升农技推广效率的同时充分发挥科技要素在推动经济发展中的积极作用.需要强调地是，高学历农民或技术能人的指导行为能够形成以其为核心的技术扩散区域，如农民专业合作社的运作模式和发展实践，有利于产生全新的技术扩散路径，进而提高农技推广效率.受灾面积在各回归方程中的系数同为正值，通过10%的显著性水平检验，表明这一变量的增加，将促使松弛变量数值提高，农技推广效率水平下降.农业灾害为非常规性变量，对农业产量和农民生产积极性造成负面影响，包含农技推广服务在内的各项生产要素投入将无法获取经济效益.

2.3 第三阶段调整后的DEA模型分析

将调整过后的投入变量和原始产出量重新代入BCC模型，得到31个省市自治区消除环境因素和随机变量后的实际农技推广效率值，具体结果见表4.

表4 2016年农技推广的综合技术效率、纯技术效率和规模效率水平

注：irs为规模效益递增；drs为规模效益递减；—为规模效益不变.

对比第一阶段和第三阶段的数据处理结果发现，在剔除随机变量和环境因素之后，国内31个省市自治区综合技术效率、纯技术效率和规模效率的平均值由原来的0.828，0.907，0.907分别下降至0.790，0.887，0.882，说明在随机变量和环境因素交互作用下的综合技术效率数值虚高.与规模效率相比，纯技术效率下降幅度较为明显，各省市自治区的农技推广纯技术效率远未达到最佳状态.第一阶段农技推广效率前沿面有江苏省、山东省，在第三阶段为江苏省；河北省、辽宁省、浙江省、湖北省、四川省和陕西省的综合技术效率值有所增加，导致其第一阶段效率值不高的主要原因有推广环境恶劣及随机因素较差等；天津市、山西省和吉林省等13个省市自治区的农技推广效率的规模报酬处于递增状态，此时增加单位推广投入要素可以带来更大收益.这种规模报酬递增的状态来源于基层农技推广人员的专业化分工、大机器设备等生产要素的集约化高效利用以及农业生产中的联合化多样化经营模式.

3 结 语

综上得出结论：① 全国范围内的农技推广效率值较高，但地区之间的差距较大，东部省市的优势明显.② 传统DEA模型无法剔除环境因素和随机变量对效率值的影响，所得结果无法准确反映国内农技推广效率的现实情况.③ 环境变量对农技推广效率的作用明显，其中国内生产总值和农技推广人员受教育程度和农民受教育水平3个变量同农技推广效率呈正相关，受灾面积与效率值的变动方向相反.④ 江苏省处于农技推广效率的前沿面，其他省份在技术管理和推广规模等环节存在较大改进空间.

提高农技推广效率的路径与改进措施如下：① 深入开发农村人力资本，着力提高广大农民的受教育水平，广泛开展农村职业技能教育与技术指导，增加其对农技理解并激发使用热情，实现生产要素的集约化利用.② 提升农技推广工作的扶持力度，利用专项补贴等形式改善基层农技推广环境和农技推广人员待遇，激发人员工作活力.③ 改变传统行政命令式的农技推广方式，重视农民需求的变化与表达，形成“自下而上”的农技扩散路径，实现农业技术供求的高度契合.④ 加强农业灾害的预警和监测，利用农业保险等方式对受灾农户给予保护，减缓农民对技术采纳的抵触情绪.⑤ 重新布局基层农技推广网络，改变现阶段“线断、网破、人散”的窘境，扩大基层农技推广人员服务范围，尤其是发展村级农技推广队伍,由新型农业经营主体和村中能人组成，解决农技推广最后一公里问题.⑥ 在贯彻落实“乡村振兴”战略的基础上，借助“互联网+农业”的发展契机，快速推进农村网络平台的建设和普及，利用现代化手段快速搜集农技信息，摆脱农技在时间和空间传播扩散中的限制，及时解决农技推广及农业生产经营困难，确保农技推广高效展开，全地区覆盖，全方位见成效.

参 考 文 献：

[1] 时悦.农业生产效率变动分析、分解及调整目标——基于DEA方法的实证研究[J].华南农业大学学报(社会科学版)，2007,6(4):30.

SHI Yue.Agricultural Production Efficiency Change,Decomposition and Adjustment Goal—An Empirical Study Based on DEA[J].Journal of South China Agricultural University(Social Science Edition),2007,6(4):30.(in Chinese)

[2] 宋增基，徐叶琴，张宗益.基于DEA模型的中国农业效率评价[J].重庆大学学报(社会科学版)，2008,14(3):24.

SONG Zengji,XU Yeqin,ZHANG Zongyi.A DEA Efficiency Analysis of Chinese Agriculture[J].Journal of Chongqing University(Social Science Edition),2008,14(3):24.(in Chinese)

[3] 亢霞，刘秀梅.我国粮食生产的技术效率分析——基于随机前沿分析方法[J].中国农村观察，2005(4):32.

HANG Xia,LIU Xiumei.Analysis of Technology Efficiency of Grain Production in China-An Empirical Research Based on the Stochastic Frontier Analysis[J].China Rural Survey,2005(4):32.(in Chinese)

[4] 雷玉桃，黄丽萍.中国工业用水效率及其影响因素的区域差异研究——基于SFA的省级面板数据[J].中国软科学，2015(4):155.

LEI Yutao,HUANG Liping.Regional Differences in Industrial Water Consumption Efficiency and Its Influencing Factors for China’s Major Industrial Provinces—A Study of Provincial Panel Data Based on SFA[J].China Soft Science,2015(4):155.

(in Chinese)

[5] 韩晶.中国高技术产业创新效率研究——基于SFA方法的实证分析[J].科学学研究，2010,28(3):467.

HAN Jing.An Empirical Analysis on China’ High-Technology Industry Innovation Efficiency Based on SFA[J].Studies in Science of Science,2010,28(3):467.(in Chinese)

[6] FRIED H O,LOVELL C A K,SCHMIDT S,et al.Accounting for Environmental Effects and Statistical Noise in Data Envelopment Analysis[J].Journal of Productivity Analysis,2002,17(1):157.

[7] CHARNES A,COOPER W W,RHODES E.Measuring the Efficiency of Decision Making Units[J]．European Journal of Operational Reasearch,1978，2(6):429．

[8] 徐晓雯,时鹏将.基于DEA和SFA的我国商业银行效率研究[J].数理统计与管理，2006，25(1):68.

XU Xiaowen，SHI Pengjiang.Efficiency Comparative Study on Commercial Bank in China Based on DEA and SFA[J].Application of Statistics and Management,2006,25(1):68.(in Chinese)

[9] 白玛雍珍.我国农业生产的技术效率及其影响因素分析——基于SFA的实证分析[J].商业经济研究，2016(23):172.

PEMA Yongzhen.A SFA Analysis of Technology Efficiency and Its Influence Factor of Chinese Agriculture[J].Journal of Commercial Economics,2016(23):172.(in Chinese)

[10] 单玉红，朱枫，刘梦娇.湖北省县际种植业生产要素调控对策研究——基于三阶段DEA模型[J].资源科学，2017,39(2):367.

SHAN Yuhong，ZHU Feng,LIU Mengjiao.Structural Regulation Countermeasures of Planting Industry Production Factors for Counties in Hubei According to Three-stage DEA Modeling[J].Resources Science,2017,39(2):367.(in Chinese)

[11] 贾帅帅，王孟欣.基于三阶段DEA的工业企业科技创新效率研究[J].科技管理研究，2017,37(16):197.

JIA Shuaishuai,WANG Mengxin.Research on the Innovation Efficiency of Industrial Enterprises Based on Three-stage DEA Model[J].Science and Technology Management Research,2017,37(16):197.(in Chinese)

[12] 王谦，李超.基于三阶段DEA模型的我国财政支农支出效率评价[J].财政研究，2016(8):66.

WANG Qian,LI Chao.Efficiency Evaluation of Fiscal Expenditure for Agriculture Based on Three-stage DEA Model [J].Public Finance Research，2016(8):66.(in Chinese)

[13] 刘亦文，胡宗义.中国碳排放效率区域差异性研究——基于三阶段DEA模型和超效率DEA模型的分析[J].山西财经大学学报，2015，37(2):23.

LIU Yiwen,HU Zongyi.Research on Regional Difference about Carbon Emission Efficiency in China—Based on Three Stage DEA Model and Super Efficiency DEA Model[J].Journal of Shanxi University of Finance and Economics,2015，37(2):23.

(in Chinese)

[14] 焦源，赵玉姝，高强.我国沿海地区农业技术推广效率及其制约因素[J].华南农业大学学报(社会科学版)，2013，12(4):12.

JIAO Yuan,ZHAO Yushu,GAO Qiang.The Study of Agriculture Extension Efficiency in Coastal Area of China[J].Journal of South China Agricultural University(Social Science Edition),2013，12(4):12.

(in Chinese)

[15] 王武科,李同升，张建忠.市场机制下的农业技术推广体系构建[J].科技进步与对策，2008，25(7):102.

WANG Wuke,LI Tongsheng,ZHANG Jianzhong.Construction of Agricultural Technology Extension System under Market Mechanism[J].Science & Technology Progress and Policy,2008,25(7):102.(in Chinese)