DYB-3 航空有机玻璃风挡鸟撞数值模拟

陈贺贺， 原梅妮， 李立州， 史明东， 何小晶， 韩玉杰， 姜 波,3

(1. 中北大学 机电工程学院， 山西 太原 030051； 2. 中国航空制造技术研究院， 北京 100024；3. 北京科技大学， 北京 100083)

0 引 言

飞鸟与飞机在空中相撞所产生的事故称为“鸟撞”. 飞鸟的撞击会给飞机造成严重后果， 甚至发生机毁人亡的事故. 风挡是飞机上重要且易遭鸟撞击的部件之一， 其抗鸟撞研究一直是每个国家在飞机设计过程中一个必不可少的过程， 风挡的设计准则要求风挡在飞机巡航速度下能够抵抗 1.8 kg 的飞鸟撞击而不击穿[1-4].

风挡鸟撞问题的研究一般采用试验或数值模拟等方法. 朱书华[5]等通过某型飞机全尺寸风挡鸟撞试验， 研究了鸟撞风挡的动响应过程， 所获结果为建立准确的鸟撞风挡有限元模型提供了重要的试验依据和验证算例. 姚小虎[6]从试验和数值模拟两方面研究了鸟撞飞机风挡的动力响应问题， 数值模拟结果与试验吻合较好， 验证了有限元模型的正确性. 另外， 由于鸟撞试验成本极为昂贵， 所以鸟撞问题的研究广泛采用数值模拟方法. 目前国内外鸟撞问题的仿真研究， 在分析方法上多运用拉格朗日(Lagrange)、 光滑粒子流体动力学(SPH)法定义鸟体模型. 王富生等[7]通过Lagrange方法建立塑性动力学鸟体模型， 采用多岛遗传算法等优化方法实现了鸟体材料参数的反演. 贾建东等[8]采用SPH方法建立鸟体有限元模型， 对某飞机圆弧风挡鸟撞过程进行了数值模拟， 计算结果与试验基本吻合； 同时与鸟体采用任意拉格朗日法(ALE)和无网格伽辽金方法(EFG)进行对比， 验证了SPH方法在分析鸟撞问题中的优越性. 朱书华等[9]还分别采用耦合解法和解耦解法研究了圆柱形和两端半球形、 中间圆柱形的鸟体形状对风挡鸟撞动响应的影响， 结果表明： 两种形状的鸟体模型计算结果与试验结果都基本相符. 王猛等[10]对一种非对称结构飞机前风挡的鸟撞动态响应进行了三维数值模拟， 计算结果表明这种非对称结构设计并不会使鸟撞风挡临界速度产生明显的降低. Uzair Ahmed Dar等[11]还研究了不同撞速和不同撞击角度下风挡的鸟撞动响应. 但在风挡鸟撞问题研究中， 影响因素众多， 目前并未对全部影响因素一一展开研究.

本文采用有限元仿真方法开展了飞机风挡鸟撞问题的研究， 重点对不同鸟体力学模型、 风挡上不同撞击位置以及风挡不同材料等因素进行了研究.

1 鸟撞飞机风挡有限元模型

1.1 Lagrange法和SPH法

在鸟撞问题仿真研究时， 鸟体模型一般采用Lagrange或SPH方法定义， 材料模型一般选择弹塑性或自定义材料模型. 其中Lagrange[12]法多用于固体力学的有限元计算中， Lagrange网格将节点固定在分析对象上， 单元由节点连接形成， 并组成网格. 网格固定在物体上随物体一起运动， 当分析对象发生变形时， 网格节点随之移动， 并与物质点始终保持重合， 同时， 单元也随之变形. SPH是Lucy等人于1977年最早提出的一种无网格粒子法， 首先被应用于解决无边界天体问题， 后逐渐在流体动力学、 侵彻、 碰撞等领域得到广泛应用. SPH把分析对象离散化， 使用固定质量的可动点即质点或节点代替网格单元， 减少了有限元法中单元划分的工作， 也没网格畸变等问题.

1.2 鸟体有限元模型

鸟体几何模型[7]采用中间圆柱、 两端半球体的实体， 长径比约为2∶1， 球体半径为0.053 m， 中间圆柱长为0.141 8 m， 鸟体质量为 1.8 kg. 采用Lagrange， SPH方法分别定义鸟体有限元模型， 在Lagrange方法中， 鸟体采用Solid164实体单元， 鸟体节点数为4 390， 单元数为3 480. 在SPH法中， 鸟体模型在后处理器LS-PrePost中被离散成光滑粒子， 粒子数为4 425. 两种鸟体有限元模型， 如图 1 所示.

在分析中， 弹塑性模型选用带有失效模式的Plastic Kinematic材料模型. 该模型采用剪切失效准则， 当鸟体应变达1.25时， 单元失效， 失效单元将从网格中自动删除. 材料参数值[7]见表 1 所示.

贾建东、 李冶方[8,13-14]等人采用自定义材料模型， 选用*MAT_NULL材料模型和*EOS_GRUNEISEN状态方程定义鸟体材料模型， 研究表明仿真结果与实验结果一致， 鸟体模型具体参数[14]， 如表 2 所示.

表 1 鸟体弹塑性模型参数Tab.1 Parameters of the bird model based on plastic kinematic

表 2 鸟体材料模型参数Tab.2 Parameters of the bird model based on hydrodynamic model

*EOS_GRUNEISEN状态方程能用两种方法确定压力与体积之间的关系， 从而判断出材料为压缩性质还是膨胀性质. 用来确定压缩性质材料的表达式为

(1)

用来确定膨胀性质材料的表达式为

P=ρ0C2μ+(γ0+aμ)E,

(2)

式中：μ=ρ/ρ0-1称为压缩系数；ρ,ρ0为即时和初始鸟体密度；C,γ0,a,S1～S3为与材料冲击压缩特征有关的常数；E为内能.

1.3 风挡有限元模型

飞机风挡模型[6,15]为单层等厚度圆弧风挡， 材料为DYB-3航空有机玻璃， 厚度为18 mm， 沿风挡表面对称线前后跨度为800 mm， 图 2 给出风挡模型及风挡表面对称线上3个位置：A点为前1/3点， 距前缘266.7 mm；B点为中点， 距前缘400 mm；C点为后1/3点， 距前缘533 mm.

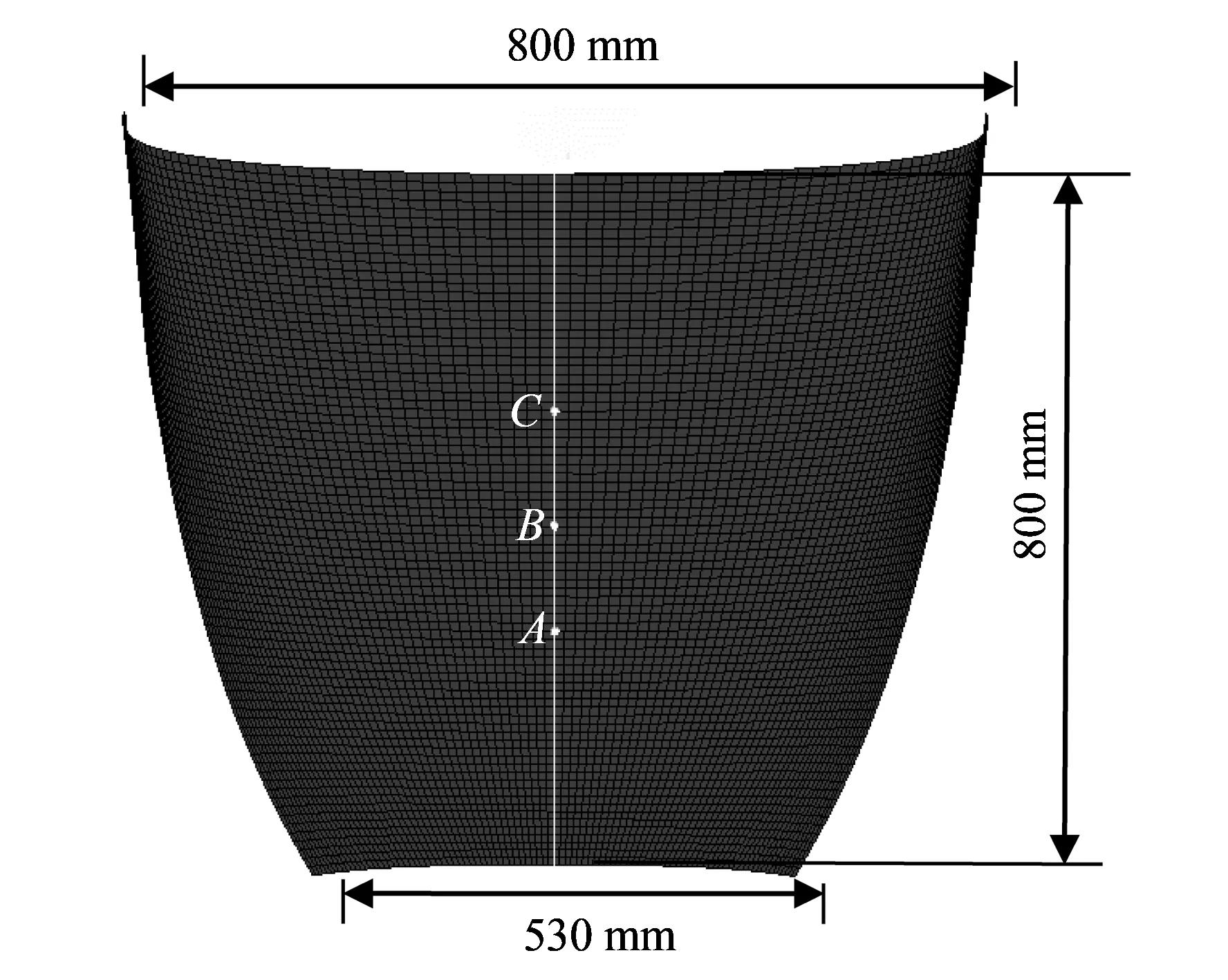
图 2 飞机风挡模型及其对称线上位置示意图Fig.2 FE model of the windshield and the position in its symmetrical line

风挡模型采用Lagrange法定义， 并采用壳单元Shell163进行网格划分， 划分单元时将前后边缘分成96份， 两侧分成80份， 风挡模型共包含7 856个节点和7 680个单元. 风挡边界采用固支约束， 材料模型选为线弹性材料， 材料参数[8]如表 3 所示. 有限元模型中鸟体与风挡接触方式选用基于罚函数的接触算法.

表 3 风挡材料参数Tab.3 Parameters of the windshield material

2 鸟体力学模型研究

选择不同材料模型和方法建立鸟体有限元模型， 研究不同鸟体模型对风挡遭撞击的动响应影响. 为了叙述方便， 对有限元模型进行编号， 见表 4， 其中风挡模型均一致， 采用线弹性模型和Lagrange方法.

对有限元模型进行仿真计算， 4种鸟体模型分别以515 km/h的速度撞击风挡对称线前1/3点， 模拟时间均为15 ms. 表 4 同时给出了4种有限元模型与试验[6]在4.5 ms时刻的撞击瞬间图， 可以看出， 此时鸟体模型滑移至风挡后部， 采用弹塑性模型的模型一和模型三鸟体变形相似， 鸟体未发生大变形； 采用自定义模型的模型二和模型四中鸟体模型表现出大变形状态， 但是采用Lagrange方法的模型二出现网格严重畸变， 会对鸟撞后风挡响应数据的精度产生影响， 而模型四中鸟体被离散成粒子， 不存在网格畸变问题， 能较好呈现鸟体在高速冲击下呈流体状飞溅的状态， 与风挡耦合效应明显， 与试验中鸟体变形模态更加接近.

表 4 4种鸟撞风挡有限元模型及4.5 ms撞击瞬间图Tab.4 Four FE models of the bird-impact windshield and the picture of impact in 4.5 ms

取4种鸟体模型中风挡对称线上中点B的位移和应变数据与试验实测数据[6]进行对比， 结果见表 5. 可以看出， 当选择弹塑性模型时， Lagrange方法的结果最优， 与试验数据相比， 误差在5%以内； 当选择自定义材料模型时， SPH方法的结果最优， 与试验数据相比， 平均误差在5%以内. 所以， 模型一和模型四均能准确预测风挡的鸟撞动态响应.

表 5 计算结果对比Tab.5 Comparison of calculation results

综上， 采用SPH方法和自定义材料的模型四可以模拟鸟体高速撞击风挡呈流体状飞溅的过程， 而且仿真结果接近试验结果， 因此模型四最适合模拟鸟撞风挡过程， 接下来选择模型四做进一步分析.

3 风挡不同撞击点处鸟撞响应

对鸟撞过程进行仿真计算， 鸟体的撞速范围是450～650 km/h， 对风挡的撞击位置分别为风挡对称线上前1/3点、 中点、 后1/3点， 对应图 2 中的A，B，C点， 模拟时间均为15 ms.

3.1 不同速度下的撞击力变化

图 3 为鸟体以不同速度撞击风挡A点时， 中间B点位置的撞击力时程曲线. 从图 3 中可以看出， 随鸟体撞击速度增大， 风挡所受撞击力也增大， 而且达到峰值的时间提前， 速度650 km/h的撞击力峰值比速度450 km/h的撞击力峰值提前0.5ms左右， 并且从图中可以看出整个鸟撞时间约4 ms. 从650 km/h的撞击力曲线可以看出， 0.9～3.4 ms为鸟体刚撞上风挡， 速度急剧减小， 风挡撞击力急剧增大， 在3.4 ms撞击力达到最大值71.8 kN； 但由于鸟体流变， 风挡表面撞击力又迅速衰减， 6.2 ms开始风挡撞击力又重新增大， 在8.4 ms左右达到峰值后又开始衰减， 这是由于鸟撞载荷冲击波回弹造成风挡所受撞击力二次增大. 速度为550 km/h和450 km/h的撞击力曲线变化趋势也类似. 这说明， 风挡遭受鸟撞之后， 一方面撞击力会迅速增大， 并向风挡周围扩散， 另一方面应力波还会在风挡中来回振荡传递， 从而对风挡不断地产生作用.

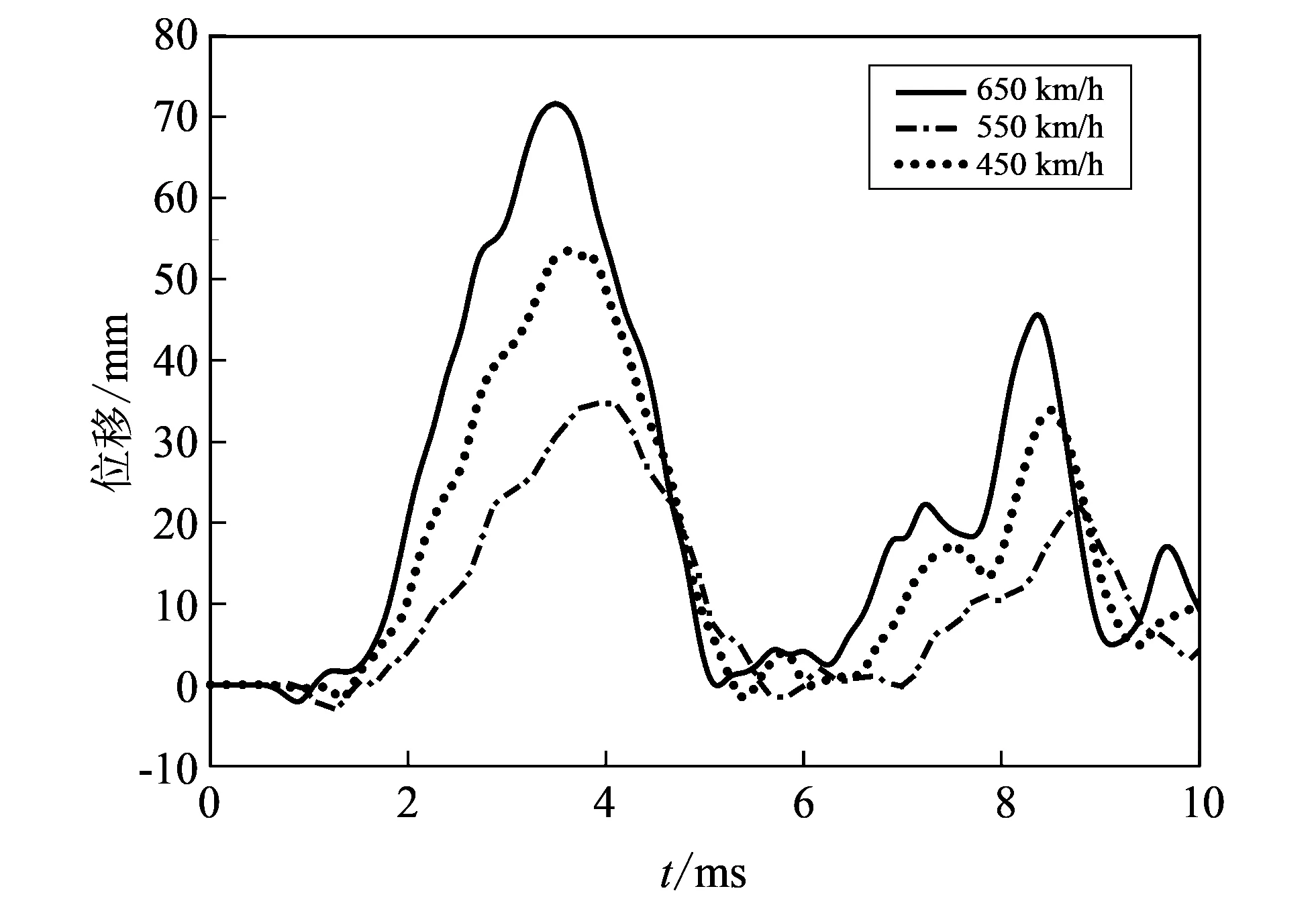
图 3 不同撞击速度下风挡的撞击力时程曲线Fig.3 Impact force history curves of windshield under different impact velocities

3.2 不同撞击点处发生失效的临界条件

有限元模型中风挡采用最大主应力失效模式， 当最大主应力达到失效强度78 MPa时[8]， 风挡单元失效. 仿真计算了风挡不同撞击位置所发生失效破坏的临界撞速及对应的临界撞击力， 见表 6.

表 6 不同撞击点的临界撞速和临界撞击力Tab.6 Critical impact velocities and force at different impact points

可以看出， 鸟撞风挡A点时， 撞击速度超过595 km/h风挡会发生失效破损， 撞击点为B点时， 风挡发生失效的临界速度为545 km/h， 撞击点为C点时， 临界撞速为480 km/h. 在风挡的3个撞击点处， 风挡发生失效破坏的临界撞速和临界撞击力在前1/3点最大， 中点次之， 后1/3点最小.

3.3 不同撞击点处的位移分析

图 4 为鸟体以562 km/h的速度撞击风挡A,B,C点时对称线上最大位移随风挡玻璃表面位置变化曲线.

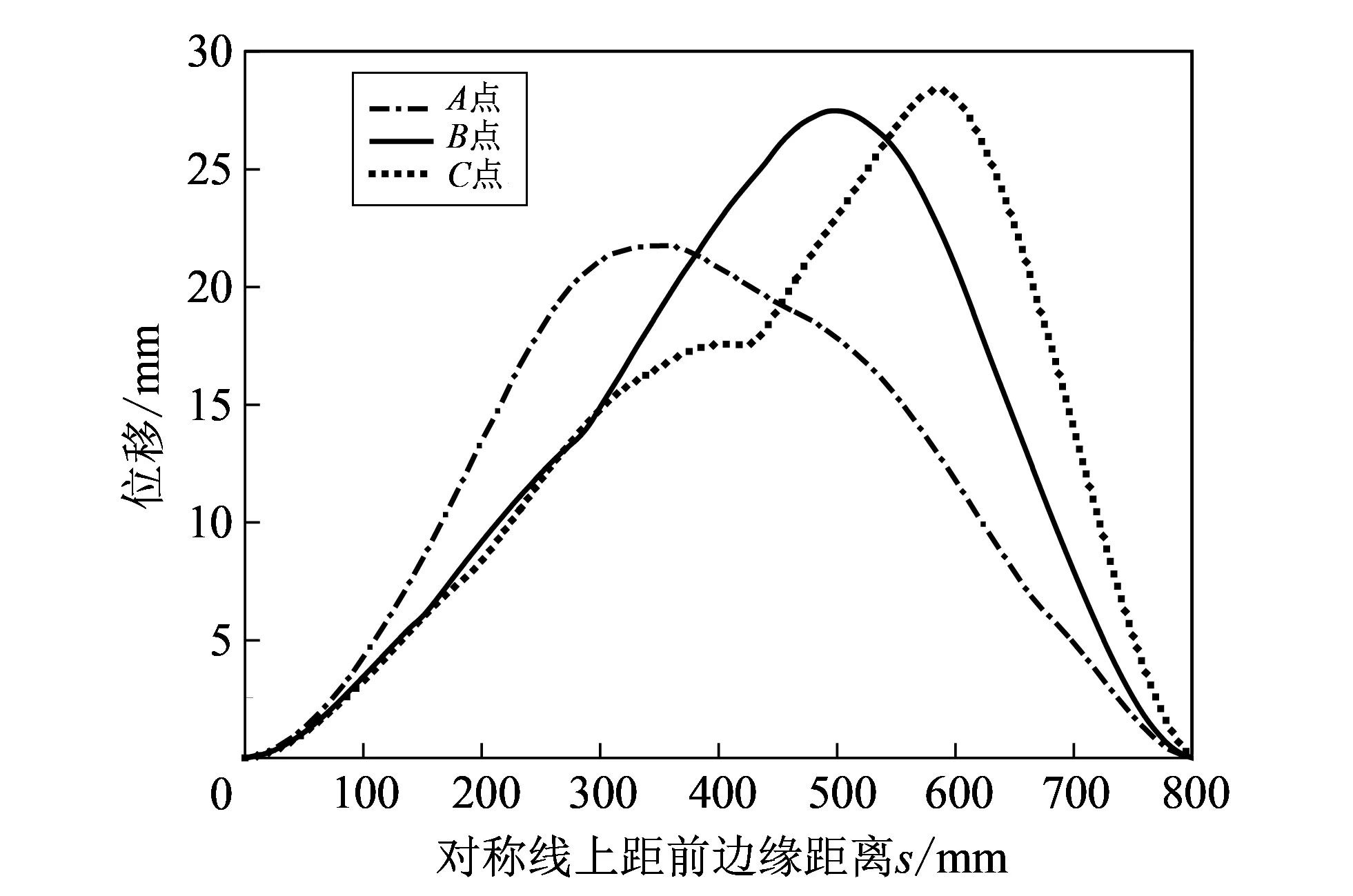
图 4 风挡对称线上最大位移随风挡表面位置变化的曲线Fig.4 The history curves of maximum displacement change with thewindshield surface position at windshield symmetrical line

当鸟体撞击风挡A点(距前边缘266.7 mm)时， 风挡位移沿风挡对称线从前往后先增大， 在距前边缘350 mm处达到最大值21.75 mm， 随着鸟体动能的逐渐减小， 风挡位移沿对称线向后逐渐减小， 由于风挡四边固支约束， 所以前边缘和后边缘的位移为0. 撞击点为B和C的曲线变化趋势类似， 撞击点为B点(距前边缘400 mm)时， 风挡对称线上最大位移为27.5 mm， 发生在距前边缘500 mm处； 撞击点为C点(距前边缘533 mm)时， 风挡对称线上最大位移为28.38 mm， 发生在距前边缘590 mm处. 可以得出， 撞击点从A点到C点， 越往后， 风挡的位移就越大， 且无论撞击点在哪， 风挡的最大位移均未发生在撞击点处， 而是在撞击点后57～100 mm处. 风挡位移达到25 mm(约风挡厚度1.4倍)以上的区域在距前边缘435～630 mm范围内， 说明风挡的最大变形发生在其中后部区域.

综上， 在风挡3个撞击点中， 前1/3点处抗鸟撞的临界速度和临界撞击力最大， 沿风挡向后的两个点依次减小； 撞击点沿风挡对称线向后， 风挡变形越大， 且最大变形发生在风挡中后部. 所以， 可以得到， 风挡前部抵抗飞鸟撞击能力最强， 中后部较弱.

4 不同风挡材料抗鸟撞性能对比分析

YB-3和DYB-3航空有机玻璃(PMMA)是国内飞机应用较广泛的两种飞机风挡材料[16]， 本节对两种风挡材料进行鸟撞性能对比分析. YB-3 PMMA的材料参数详见文献[5].

表 7 为两种材料风挡不同撞击位置的临界撞速， 可以看出YB-3 PMMA风挡发生失效的临界撞速为310～385 km/h， 小于 DYB-3 PMMA风挡临界撞速.

表 7 两种材料风挡的临界撞速Tab.7 Critical impact velocities of windshield by two materials symmetrical line

鸟体以350 km/h的速度分别撞击DYB-3和YB-3 PMMA风挡A点时， 获得了B点的位移时程曲线(见图 5)， 以及B点的应变时程曲线(见图 6).

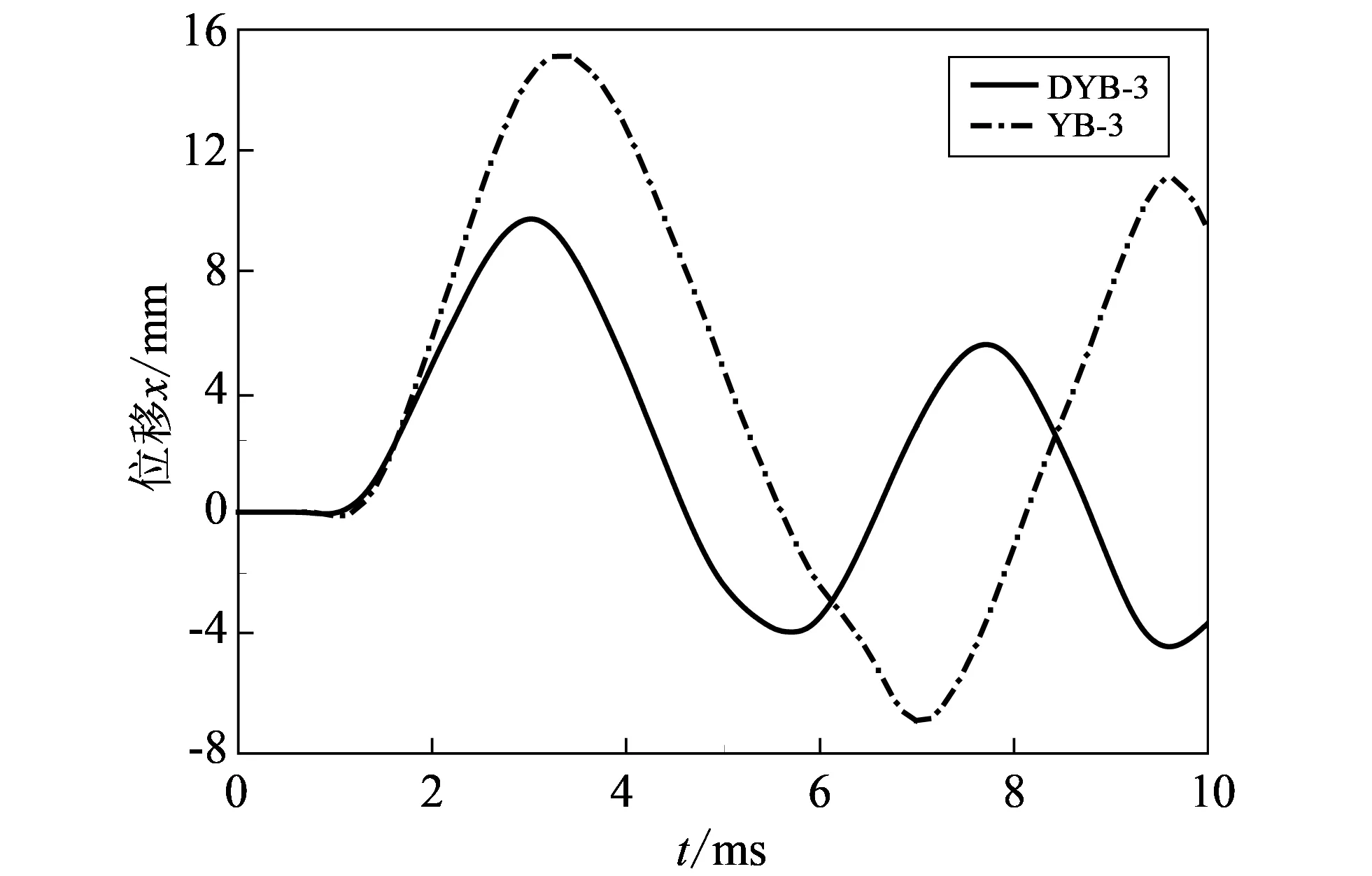
图 5 两种材料风挡位移时程曲线Fig.5 Displacement history curves of windshield by two materials

由图 5 可以看出， YB-3 PMMA的位移峰值为15.2 mm， 大于DYB-3 PMMA的最大位移9.7 mm， 但DYB-3 PMMA的位移时程曲线频率大于YB-3 PMMA； 由图 6 可以看出， YB-3 PMMA的应变峰值为10.5×10-3， 大于DYB-3 PMMA应变峰值近一倍. DYB-3 PMMA刚度相对较大、 变形较小， 从而风挡位移、 应变较小， 但遭鸟撞后发生振荡的频率较大.

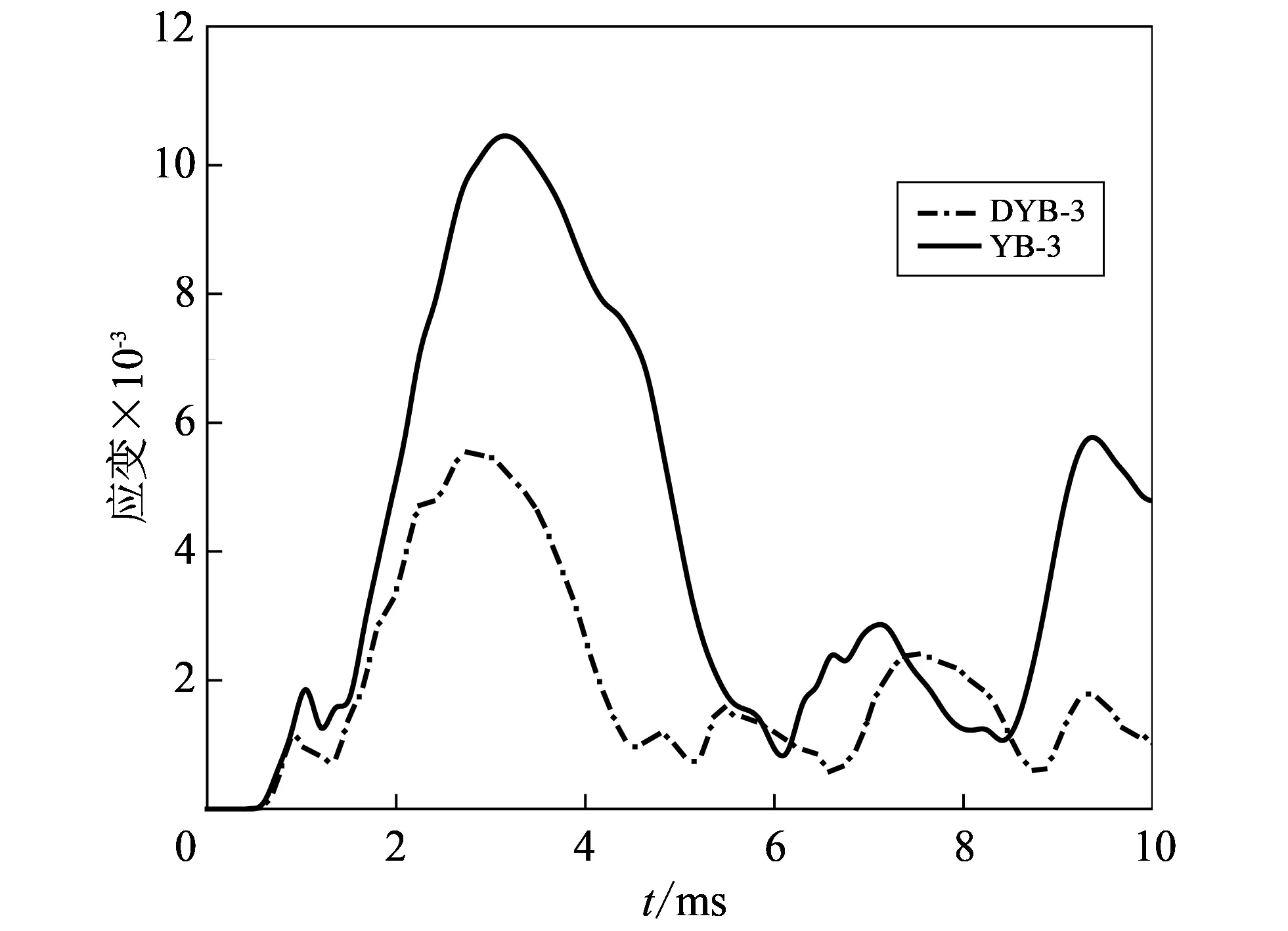
图 6 两种材料风挡应变时程曲线Fig.6 Strain history curves of windshield by two materials

综上可以看出， DYB-3 PMMA风挡在鸟撞仿真中表现出较高的耐冲击性， 而且DYB-3 PMMA是由YB-3板定向拉伸而成， 分子链经过拉伸取向后， 使其具备更好的抗银纹和抗裂纹扩展等性能[16]. 所以， DYB-3 PMMA更适合用在气动载荷较大的部位或者巡航速度较大的飞机风挡.

5 结 论

1)采用SPH方法和自定义材料的鸟体模型可以模拟鸟体高速撞击风挡呈流体状飞溅的过程， 并能准确预测风挡的鸟撞动态响应.

2)风挡所受撞击力随鸟体撞击速度增大而增大， 且达到峰值的时间提前. 飞鸟撞击风挡对称线前1/3点时， 风挡发生失效破坏的临界撞速和临界撞击力较大， 中点次之， 后1/3点最小.

3)撞击点从前1/3点到后1/3点， 越往后， 风挡鸟撞后的位移就越大； 无论撞击点在哪， 风挡的最大位移均未发生在撞击点处， 而是在撞击点后57～100 mm处； 风挡位移达到25 mm(约风挡厚度1.4倍)以上的区域在距前边缘435～630 mm范围内.

4) DYB-3 PMMA风挡在鸟撞仿真中表现出较高的耐冲击性， 适合用在气动载荷较大的部位或者巡航速度较大的飞机风挡.

参考文献：

[1] 李玉龙, 石霄鹏. 民用飞机鸟撞研究现状[J]. 航空学报, 2012, 33(2)： 189-198.

Li Yulong, Shi Xiaopeng. Investigation of the present status of research on bird impacting on commercial airplanes[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(2)： 189-198. (in Chinese)

[2] Mccarty R, Gran M, Baruch M. MAGNA nonlinear finite element analysis of T-46 aircraft windshield bird impact[C]. Aircraft Systems, Design and Technology Meeting, 2013: 263.

[3] 王富生, 岳珠峰, 冯震宙, 等. 鸟撞飞机风挡动态响应数值模拟方法研究现状[J]. 飞机设计, 2008, 28(5)： 39-46.

Wang Fusheng, Yue Zhufeng, Feng Zhenzhou, et al. Present study of numerical simulation methods of dynamic response for aircraft windshield under bird strike[J]. Aircraft Design, 2008, 28(5)： 39-46. (in Chinese)

[4] Mohagheghian I, Wang Y, Zhou J, et al. Deformation and damage mechanisms of laminated glass windows subjected to high velocity soft impact[J]. International Journal of Solids & Structures, 2017(109)： 46-62.

[5] 朱书华. 鸟撞飞机风挡动响应分析与仿真试验平台研究[D]. 南京： 南京航空航天大学, 2009.

[6] 姚小虎. 鸟撞飞机圆弧风挡的实验研究及数值模拟[D]. 太原： 太原理工大学, 2001.

[7] 王富生, 李立州, 王新军， 等. 鸟体材料参数的一种反演方法[J]. 航空学报, 2007, 28(2)： 344-347.

Wang Fusheng, Li Lizhou, Wang Xinjun, et al. A method to identify bird’s material parameters[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2)： 344-347. (in Chinese)

[8] 贾建东, 李志强, 杨建林, 等. 用SPH和有限元方法研究鸟撞飞机风挡问题[J]. 航空学报, 2010, 31(1)： 136-142.

Jia Jiandong, Li Zhiqiang, Yang Jianlin, et al. A study of bird impact on aircraft windshield using SPH and finite element method[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(1)： 136-142. (in Chinese)

[9] 朱书华, 童明波. 鸟体形状对飞机风挡鸟撞动响应的影响[J]. 南京航空航天大学学报, 2008, 40(4)： 551-555.

Zhu Shuhua, Tong Mingbo. Study on dynamic responses of bird striking an aircraft windshield and virtual test platform[J]. Nanjing University of Aeronautics and Astronautics, 2009： 16-86. (in Chinese)

[10] 王猛, 黄德武, 罗荣梅. 飞机前风挡非对称结构的鸟撞数值模拟[J]. 机械科学与技术, 2012, 31(2)： 291-294.

Wang Meng, Huang Dewu, Luo Rongmei. Simulating aircraft’s asymmetrical windshield subjected to bird impact[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(2)： 291-294. (in Chinese)

[11] Dar U A, Zhang W, Xu Y. FE analysis of dynamic response of aircraft windshield against bird impact[J]. International Journal of Aerospace Engineering, 2013(4)： 1-12.

[12] 李利莎, 谢清粮, 郑全平, 等. 基于Lagrange、 ALE和SPH算法的接触爆炸模拟计算[J]. 爆破, 2013, 28(1)： 18-22.

Li Lisha, Xie Qingliang, Zheng Quanping, et al. Numerical simulation of contact explosion based on Lagrange ALE and SPH[J]. Blasting, 2013, 28(1)： 18-22. (in Chinese)

[13] 张志林, 张启桥, 李铭兴. 飞机圆弧风挡鸟撞动响应分析[J]. 航空学报, 1992, 13(9)： A538-A542.

Zhang Zhilin, Zhang Qiqiao, Li Mingxing. Bird impact dynamic response analysis for aircraft arc windshield[J]. Acta Aeronautica et Astronautica Sinica, 1992, 13(9)： A538-A542. (in Chinese)

[14] 李冶方. 风挡鸟撞模型的有限元分析[D]. 郑州： 郑州大学, 2013.

[15] 白金泽. 基于神经网络方法的鸟撞飞机风挡反问题研究[D]. 西安： 西北工业大学, 2003.

[16] 秦瑞祥, 欧迎春, 张保军, 等. YB-3与DYB-3航空有机玻璃综合性能对比[J]. 中国建材科技, 2011(1)： 29-31.

Qin Ruixiang, Ou Yingchun, Zhang Baojun, et al. The contrast of competitive properties between YB-3 and DYB-3 aviation sheet[J]. China Building Materials Science & Technology, 2011(1)： 29-31. (in Chinese)