基于改进型主元分析和SVR的煤矿瓦斯涌出量预测
2018-06-04张文东
张文东, 胡 彧
(太原理工大学 测控技术研究所, 山西 太原 030024)
0 引 言
煤炭是我国重要的基础能源之一, 在我国的社会发展过程中扮演着重要的角色. 但是, 大多煤矿地形复杂, 分布广泛, 各种灾害的发生也一直伴随着煤矿的开采过程. 其中由瓦斯涌出造成的事故后果极为严重, 人员伤亡惨重, 经济损失巨大. 瓦斯涌出是在煤矿井建设和生产过程中, 受采动影响的煤层、 岩层以及被采落的煤和岩石内向矿井下空间释放瓦斯的现象, 也有学者将其形象地描述为“霰弹”模型[1]. 国内外对瓦斯引起的各种灾害评估也一直在进行, 如使用模糊评价方法对瓦斯风险的评估[2]. 若能提前预测则会使损失降到最低, 因此对瓦斯涌出量的准确预测对于煤矿安全作业就显得尤为重要. 从国内的研究近况来看, 矿井瓦斯涌出量的主要预测方法有: 矿山统计法、 分源预测法和各种基于数据挖掘技术的预测方法等. 矿山统计法是生产矿井根据以往生产过的矿井、 采区或工作面的相对瓦斯涌出量与开采深度的统计规律, 对未回采区域的相对瓦斯涌出量进行预测的一种预测方法[3]. 它是建立在准确的统计资料的基础之上, 虽然模型较简单, 但预测精度较差. 分源预测法实质是按照矿井生产过程中瓦斯涌出源的多少、 各个涌出源瓦斯涌出量的大小, 来预测矿井、 采区、 回采面和掘进工作面等的瓦斯涌出量[4]. 在现实情况中的煤矿地质分布情况有很大差别, 最终预测结果必然会有一些误差. 近年来, 基于数据挖掘技术的预测方法也被用被用于瓦斯涌出量的预测, 并能够达到一定的预测精度[5], 但其中大部分方法都需要足够多的样本和较大的计算量.
煤矿矿井的瓦斯涌出受到各种各样自然因素以及环境因素的影响, 并且其具有多变性和不均衡性的特点. 基于上述原因, 难以对煤层瓦斯的涌出量有一个准确、 及时的预测, 这会直接影响到煤矿的安全生产与瓦斯防治. 本文运用基于Spearman相关系数加权改进后的主元分析SPCA(Spearman Principal Component Analysis, SPCA)和支持向量回归机Support Vector Regression, SVR)技术对瓦斯涌出量进行预测研究, 取得了较好的预测效果.
1 主元分析
1.1 主元分析基本原理
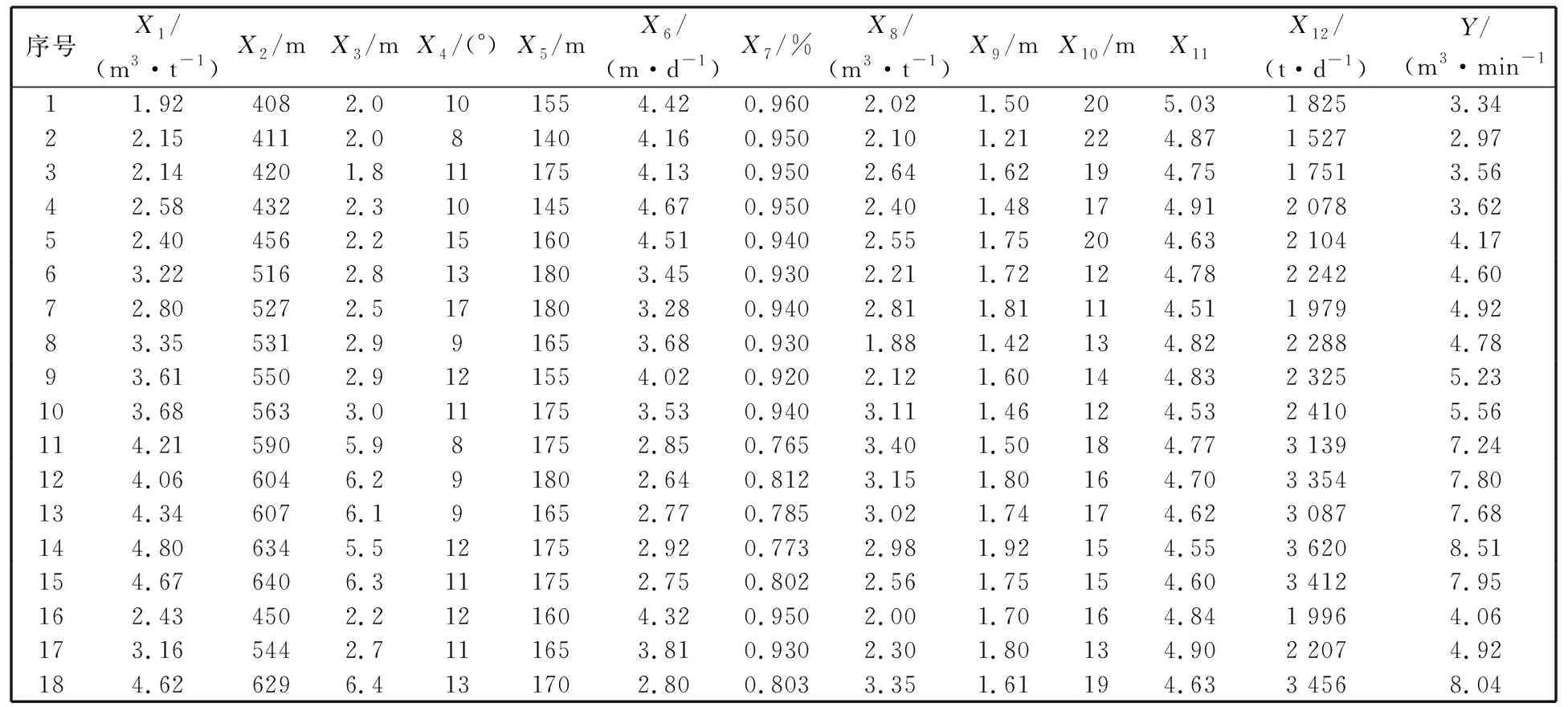
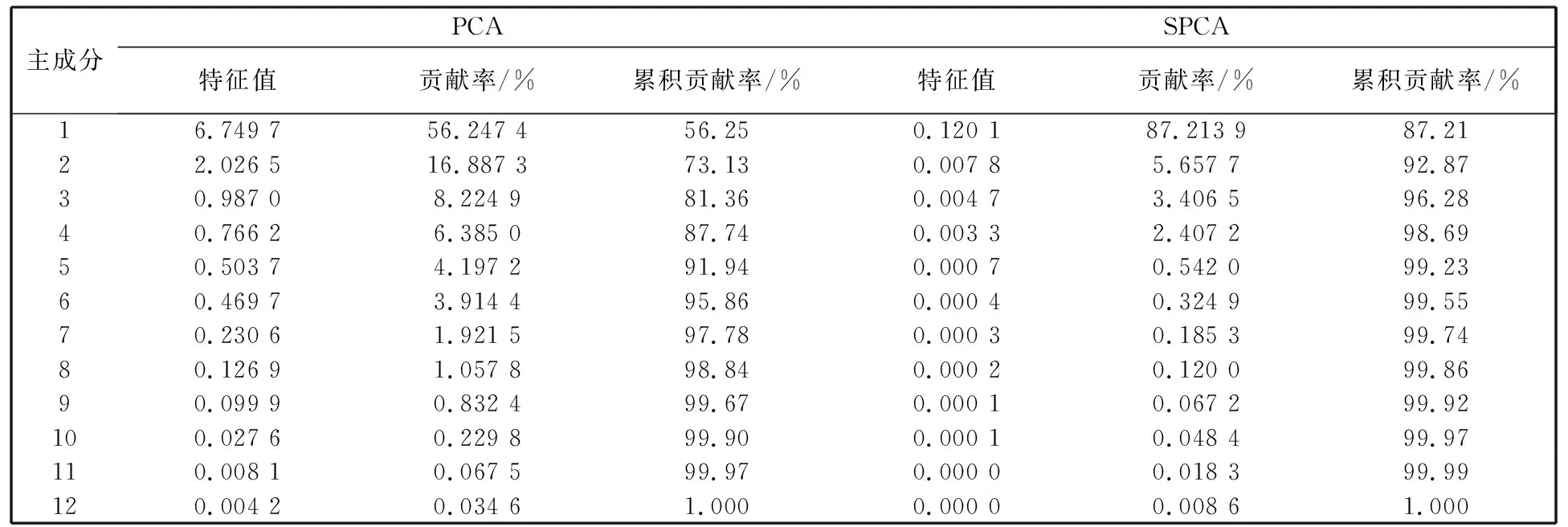
由于现代科技进步及人类社会的不断发展, 人们接触到的信息和数据越来越多, 这些数据很多都是高维的, 伴随这些数据而来的就是维数灾难. 高维的数据通常具有很多特征, 包含有大量的冗余和无关信息, 而这在很大程度上会影响机器学习的效率[6]. 这种情况需要一种特征降维的方法来减少数据的特征数、 数据噪音、 冗余及过度拟合的可能性. 而PCA就是这样一种专门用于处理此类情况的分析并且简化数据集的技术. PCA将输入变量中可能或近似相关的变量通过数学变换转化成为线性无关的变量, 是一种丢失原始数据集信息最少的线性降维方式[7]. 通过降维,可以降低数据的特征维度, 减少冗余信息所造成的误差,提高识别(回归、 聚类)的精度. PCA的算法思想是将n维特征映射到k维上(k 由于不同的变量特征常常具有不同的单位和不同的变异程度, 当特征自身具有较大差异的变异时, 会使得计算出的关系系数中, 各个特征所占的比重不同. 为了消除不同单位量纲和数值大小的影响, 需要将数据集标准化[8]. 而标准化通常也是进行正式主元分析前的一个重要步骤. 但是, 在数据标准化后, PCA在处理过程中会平等地对待每一维特征, 也即每一维特征的权重都是相等的. 实际上不同的特征向量对最终分类(回归、 聚类)的作用是不同的, 假如我们对数据的特征已经有了一些先验知识却并不能把它用在PCA的处理过程中, 无疑会对后续的机器学习的预测结果有一定的影响. 针对这个问题, 本文使用了Spearman相关分析, Spearman相关分析是利用原始的两变量的秩次大小来进行线性相关分析, 它对变量的分布没有要求, 因此适用范围较广, 是一种比较通用的相关分析方法[9]. 对标准化后的数据特征进行Spearman相关分析, 分别求出每维特征与最终结果向量的相关性, 根据相关系数赋予每维特征合适的权值, 得出新的数据矩阵交由PCA进一步处理, 这种算法称为SPCA. SPCA算法的具体步骤为: 1) 给定原始训练样本Xm×n, 它由m个样本,n个特征组成; 2) 对原始数据集进行标准化, 得到标准化后的矩阵Ym×n; 3) 对标准化矩阵Ym×n的每一维特征分别与结果向量Lm×1进行Spearman相关分析, 得到相关系数矩阵 其中,rjj(j=1,2,…,n)为第j维特征向量与结果向量的相关系数; 4) 根据Spearman秩相关系数临界值表, 结合数据样本数量选择对应的临界值, 由于这些相关值的大小一定程度上说明了其对应特征与最终结果的相关程度, 而临界值以下的特征对于最终结果的影响很小, 所以对临界值以下的相关系数赋予一个合适的较低的值作为对应特征向量的权重(经多次实验权衡后本文选为0.1), 其它特征向量的权重为其各自对应的相关系数; 5) 将矩阵Ym×n的每一列向量, 乘以其对应的权重得矩阵 6) 求出协方差矩阵 7) 求出矩阵C的特征值以及C对应的特征向量 λjαj=Cαj, (j=1,…,n), 其中,λj为矩阵的特征值,αj为特征向量; 8) 将特征向量按对应特征值λj的大小从大到小排列成矩阵, 并依据λj的值计算主成分的贡献率和累积贡献率, 通常以85%为界限确定前k个主成分; 9) 由k个主成分组成的新矩阵即为降维后的数据矩阵Im×k. 支持向量机是由Vapnik领导的AT&TBell实验室研究小组在1963年提出的一种新的通用学习方法, 它是一种基于统计学习理论的模式识别方法, 主要应用在模式识别领域, 它在解决样本数量少、 非线性问题和高维模式识别等方面相比其它算法具有很大的优势[10]. 支持向量机在一定程度上克服了“过学习”和“维数灾难”等问题, 被称为数据挖掘领域的十大经典算法之一[11]. 支持向量回归机(SVR)是支持向量机(SVM)的回归算法, SVR的主要思想是在原始训练数据的特征空间中寻找一个具有最大分割距离的超平面, 通过引入损失函数, 用于解决回归问题, 其本质就是寻找一个最优的分类面使所有训练样本离这个最优分类面的距离误差最小. SVR的基本思想是将影响因素作为输入变量(x1,x2,x3,…,xm)映射到一个高维的特征空间(φ(x1),φ(x2),φ(x3),…,φ(xn)), 将非线性模型转化为一个在高维特征空间中的线性回归模型,其线性回归函数形式为 f(xi)=ωTφ(xi)+b, 式中:f(xi)为回归函数返回的预测值;ω为权重向量;φ(xi)为非线性映射函数;b为阈值. 利用最小化结构风险的原理, 得到经验风险函数 式中:C(ej)是损失函数; ‖ω‖2是置信风险. 求经验风险函数的最小值, 等同于求解以下式子最小值的优化问题 为了求解上式, 引入Lagrange函数并将以上问题转化成为对偶问题, 可得对偶函数为 在求解上述问题后可得非线性回归函数 其中,K(xi,x)为核函数, 与多项式核函数、 线性核函数和sigmoid核函数等相比, 高斯核函数存在适用性广, 参数少等优势[12], 再结合文献利用各种核函数经过实验仿真得出的结果分析, 使用高斯核作为SVM的核函数训练出的模型是最合适的. 故本文拟采用高斯核函数:K(xi,x)=exp(-γ‖xi-x‖2). 经过上述分析可知, 只需确定惩罚因子C和参数γ便可得到预测模型. 基于上文的分析, 本文将SPCA与SVR结合来进行建模, 具体操作步骤如下: 1) 将原始数据集Dm×n标准化处理, 消除各维特征之间量纲影响, 得到新数据集Sm×n; 2) 按照1.2节SPCA算法步骤对矩阵Sm×n进行分析处理, 得到新矩阵Pm×n; 3) 在矩阵Pm×n中, 根据每维特征的贡献率大小, 选取贡献率为85%以上所对应的前k维特征(若要求精度, 也可选取90%或更高的贡献率)组成矩阵Im×k; 4) 将矩阵Im×k按照合适的比例分为训练集Im1×k和测试集Im2×k(注:m1+m2=m); 5) 将训练集Im1×k及其所对应的结果作为SVR的输入并按照第2节算法步骤进行学习训练, 得到最终预测函数为 6) 将测试集Im2×k中的样本代入预测函数中, 求出预测值并与实际值对比, 得到模型的预测精度. 整个算法流程如图 1 所示. 图 1 预测模型算法流程Fig.1 Process of prediction model algorithm 瓦斯涌出的多少受到很多种因素的影响, 主要的影响因素有开采因素、 自然因素、 地质因素等, 其中煤层的地质因素是影响矿井瓦斯涌出的最重要条件之一[12]. 本文结合某煤矿18个月回采工作面的统计数据进行分析, 采集到的因素有原始瓦斯含量、 煤层埋深、 煤层厚度、 开采强度等12个相关因素, 完整的数据如表 1 所示(其中,X1为煤层瓦斯含量,X2为煤层埋深,X3为煤层厚度,X4为煤层倾角,X5为工作面长度,X6为推进速度,X7为工作面采出率,X8为邻近层瓦斯含量,X9为邻近层厚度,X10为层间距,X11为层间岩性,X12为开采强度,Y为瓦斯涌出量)[13]. 在本例中, 选取前15个样本进行学习训练, 后3个样本用来预测并与真实值对比, 也就是1~15号为训练集, 16~18号为测试集. 根据上文分析, 用Matlab软件对原始数据进行标准化和SPCA处理, 在维持高信息的前提下简化模型的复杂度. 同时, 为了对比, 也对数据进行了传统的PCA处理, 分析结果如表2所示. 可以看到, 相比PCA而言, 用SPCA方法得到的第一主元素的贡献率为87.21%, 而用传统PCA方法得到的第一主元素的贡献率仅为56.25%, SPCA仅前三维的累积贡献率就超过了95%, 而PCA需要前六维主成分才可达到这一数据. 由此可见, 本文提出的改进型SPCA算法的降维效果良好. 接下来选择累积贡献率超过85%的主元作为SVR的输入变量, 瓦斯涌出量作为输出. 按照3.1节求解步骤, 选择表1中的样本1~15号进行SVR训练, 其中SVR中核函数的参数和参数经优化算法分别求得为7.755和0.012, 然后对样本16~18号用训练出的模型进行预测并检验. 拟合仿真结果见图 2 所示. 表 1 煤矿回采面瓦斯的涌出量与影响因素关系表Tab.1 Relationship between gas emission and influencing factors in coal mining face 表 2 PCA与SPCA分析结果Tab.2 Analysis results of PCA and SPCA 图 2 SPCA-SVR模型预测的训练值及测试值与实际值的对比Fig.2 Comparison of the training and testing values with the actual values predicted by SPCA-SVR model 可以看到, 利用SPCA-SVR模型的预测值与实际值拟合较好, 为了对比分析, 本文还对相同的样本分别利用SVR、 PCA-SVR、 矿山统计法和BP-NN模型进行了预测分析. 关于矿山统计法预测, 由于在瓦斯地带, 通常情况下相对瓦斯涌出量与开采深度近似呈线性相关, 因此矿山统计法实质上是求一个线性回归方程, 预测模型简单, 预测结果精度较差. BP-NN, 即BP神经网络, 是由输入层, 隐含层和输出层三层构成, 是引用比较广泛的神经网络模型之一, 它的学习过程由正向传播信号和反向传播误差组成, 每一次的误差反传都将对各层的各个单元的权值进行调整, 通过不断迭代, 达到一定的学习次数或者使最终误差达到一个合适的水平为止[14]. 该方法模型较为复杂, 学习速度较慢. 本文用Matlab软件对上述预测方法进行仿真, 训练预测结果如表 3 所示, 仿真拟合结果如图 3 所示, 其中偏差值为实际值与预测值差的绝对值. 由图 3 可见, 相比来说SPCA-SVR模型的预测效果要优于其他4种模型的预测效果. 为了更加直观地展示模型预测性能的优劣, 本文选用测试集中预测值与实际值的均方误差(MSE)和平均相对误差(MAPE)来评价模型的性能好坏. 均方误差和平均相对误差的计算公式分别为 (i=1,2,3,…,m), 表 3 5种训练模型的预测值与实际测试值的偏差Tab.3 Deviation between predictive values of five models and actual values (m3·min-1) 图 3 5种模型的实际测试值与训练预测值仿真Fig.3 Simulation of the actual values and predictive values of five models 根据以上公式计算得到5个模型的性能指标评价如表 4 所示. 表 4 模型评价Tab.4 Model evaluation 数理统计中均方误差(MSE)是指参数估计值与参数真值之差平方的期望值. MSE可以评价数据的变化程度, MSE的值越小, 说明预测模型描述实验数据具有更好的精确度. 从表 4 中可以看到矿山统计法预测精度最差, 也从侧面证实了其实质上是求一个线性回归方程, 预测模型简单, 使得预测结果精度较差. BP-NN、 SVR、 PCA-SVR三者的均方误差和平均相对误差都比较低且较为接近, 说明这3种模型都比较适用于瓦斯涌出量的预测, 而多数文献中也正是应用BP-NN模型和SVR模型来进行预测. 与单纯的SVR相比, PCA-SVR的均方误差和平均相对误差都较低, 说明利用PCA进行前期处理起到了一定作用, 减少了冗余信息所造成的误差. SPCA-SVR则在PCA-SVR的基础上对PCA进行加权改进, 更加优化了其去噪及降维能力, 使均方误差和平均相对误差更低, 预测精度进一步提高. 1) 煤矿瓦斯涌出受多种因素共同影响, 针对PCA提取特征上存在的缺点, 提出了一种基于权重的改进型PCA, 即SPCA, 经实验仿真结果证明, SPCA的降维能力要优于PCA. 由于对初始数据的每维特征赋予了合适的权值, 使得处理结果更客观, 在所包含的信息累积贡献率相同或相近的情况下, 经SPCA处理后的数据的特征维数较之传统PCA明显要少, 可以减少训练时间, 减小系统复杂度. 2) 根据SPCA和SVR的原理, 针对小样本的特点, 建立了基于SPCA-SVR的煤矿瓦斯涌出量预测模型. 为了与本文提出的模型对比, 分别利用了单独的SVR模型、 PCA-SVR模型、 矿山统计法和BP-NN模型来进行预测, 结果表明这4种方法的预测精度在一定程度上都不及本文提出的SPCA-SVR模型的预测精度. 由于Spearman相关系数和PCA算法本身存在的特点, 当数据的特征与因变量之间近似成线性关系或低阶相关时该方法预测结果比较准确, 通常鉴于煤层瓦斯的涌出量与其主要影响因素之间大多不会存在太过复杂的高阶相关, 所以, 本文提出的方法比较适合于瓦斯涌出量的预测, 并且预测效果也较好. 参考文献: [1] 逄焕东, 高文乐, 杨永杰. 煤与瓦斯突出的“霰弹”模型及其变化规律[J]. 中国科技论文, 2015, 10(3): 296-299. Pang Huandong, Gao Wen Le, Yang Yongjie. Grapeshot model of coal-gas outburst and its transformation law[J]. China Sciencepaper, 2015, 10(3): 296-299. (in Chinese) [2] Nuotan W U, Luo W, Tang X. Fuzzy evaluation method based on coal mine gas explosion risk assessment[J]. Mineral Engineering Research, 2015, 30(2): 22-26. [3] 赵鹏伟. 矿山统计法预测综放工作面瓦斯涌出量[J]. 机械管理开发, 2006(3): 18-19. Zhao Pengwei. Combined roof blasting face firedamp gush aount forecasting with mine statistical methd[J]. Mechanical Management and Development, 2006 (3): 18-19. (in Chinese) [4] 徐涛, 郝彬彬, 张华. 分源预测法在新建矿井瓦斯涌出量预测中的应用[J]. 煤炭技术, 2009, 28(7): 104-106. Xu Tao, Hao Binbin, Zhang Hua. Application of forecast from different sources in new mine gas emission forecast[J]. Coal technology, 2009, 28(7): 104-106. (in Chinese) [5] Li R, Shi S, Wu A, et al. Research on prediction of gas emission based on self-organizing data mining in coal mines[J]. Procedia Engineering, 2014, 84(4): 779-785. [6] 王永欣, 张化祥, 王爽. 基于属性加权的主成分分析算法[J]. 济南大学学报(自然科学版), 2015, 29(6): 438-443. Wang Yongxin, Zhang Huaxiang, Wang Shuang. An attribute-weighted principal-component analysis algorithm[J]. Journal of University of Jinan (Science and Technology), 2015, 29(6): 438-443. (in Chinese) [7] 钟用禄, 李海山, 刘发圣, 等. 基于PCA-SVR的燃煤锅炉NOx排放预测[J]. 热力发电, 2015(1): 87-90. Zhong Yonglu, Li Haishan, Liu Fasheng, et al. PCA-SVR model based NOxemissions prediction for coal-fired boilers[J]. Thermal Power Generation, 2015(1): 87-90. (in Chinese) [8] 卢国斌, 康晋恺, 白刚, 等. PCA-BP 在回采工作面瓦斯涌出量预测中的应用[J]. 辽宁工程技术大学学报, 2015, 34(12): 1329-1334. Lu Guobin, Kang Jinkai, Bai Gang, et al. Application of PCA - BP to gas emission prediction of mining working face[J]. Journal of Liaoning Technical University(Natural Science), 2015, 34(12): 1329-1334. (in Chinese) [9] Puth M T, Neuhäuser M, Ruxton G D. Effective use of Spearman’s and Kendall’s correlation coefficients forassociation between two measured traits[J]. Animal Behaviour, 2015(102): 77-84. [10] Vapnik V. The Nature of Statistical Learning Theory[M]. New York: Springer Verlag, 1995. [11] Settouti N, Bechar M E A, Chikh M A. Statistical comparisons of the top 10 algorithms in data mining for classication task[J]. International Journal of Interactive Multimedia & Artificial Intelligence, 2016, 4(1): 46-51. [12] 杨驭东. 基于数据挖掘技术的瓦斯涌出量预测方法研究[D]. 内蒙古: 内蒙古科技大学, 2013. [13] 朱红青, 常文杰, 张彬. 回采工作面瓦斯涌出BP神经网络分源预测模型及应用[J]. 煤炭学报, 2007, 32(5): 504-508. Zhu Hongqing, Chang Wenjie, Zhang Bin. Different-source gas emission prediction model of working face based on BP artificial neural network and its application[J]. Journal of China coal society, 2007, 32(5): 504-508. (in Chinese) [14] Zhang L, Wang F, Sun T, et al. A constrained optimization method based on BP neural network[J]. Neural Computing & Applications, 2016, 7(11): 1-9.1.2 基于加权改进的主元分析
2 支持向量回归机
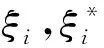
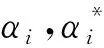
3 基于SPCA-SVR的瓦斯涌出量预测模型
3.1 预测模型的建立
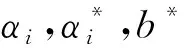

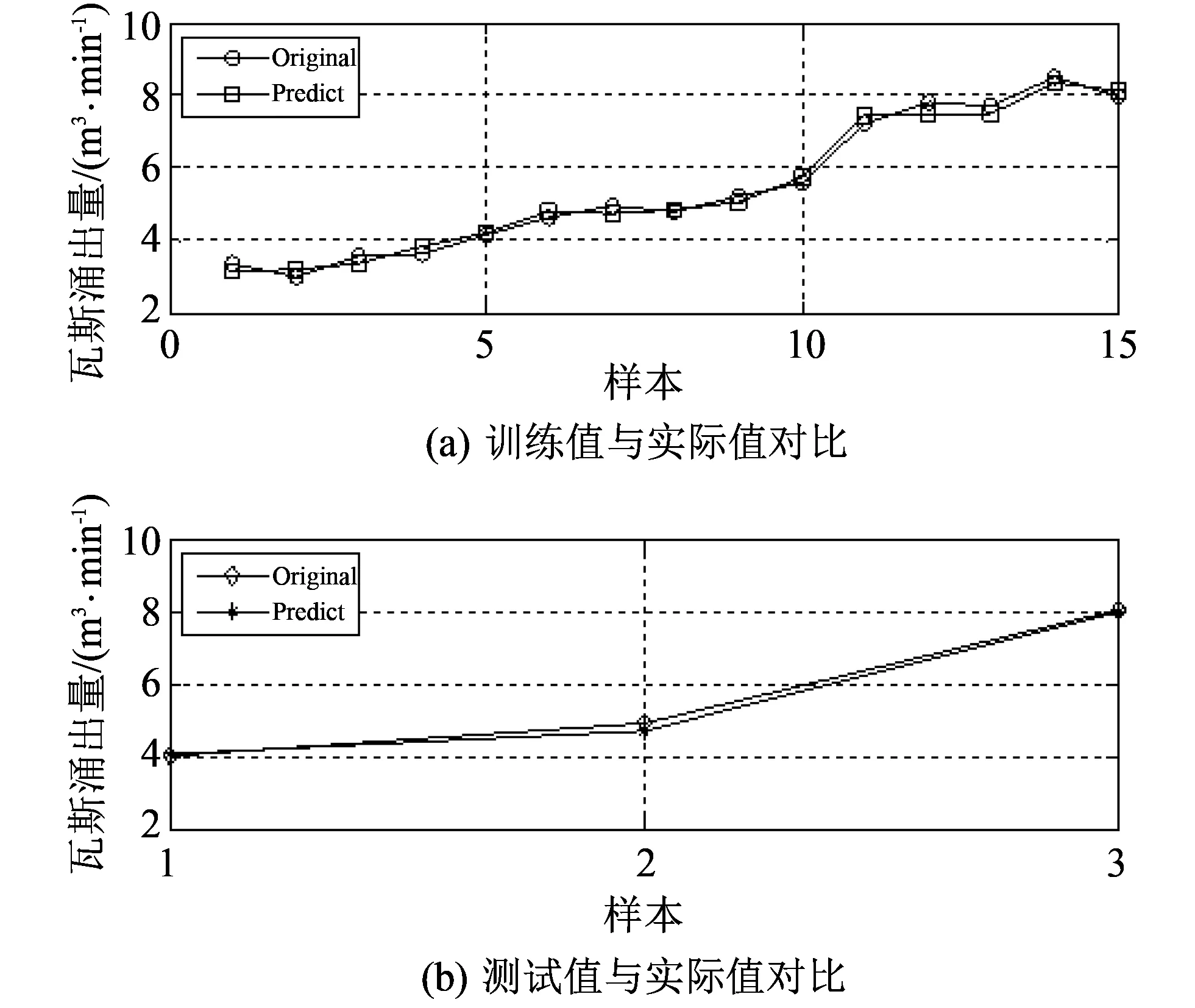
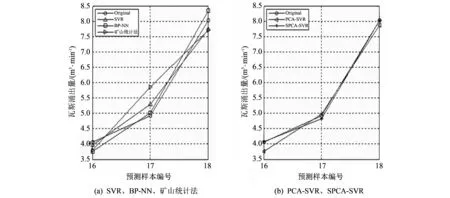
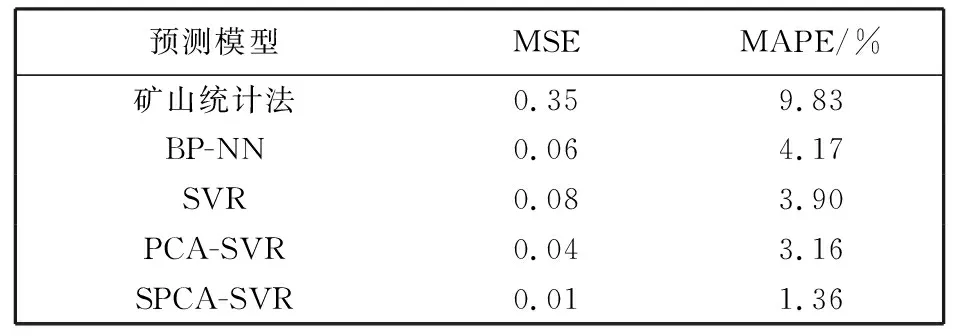
3.2 煤矿瓦斯涌出量预测实验仿真


4 结 论
