功率耦合与阻感比结合的MMC-RPC新型下垂控制策略

宋平岗，周振邦，林家通，董 辉

（1.华东交通大学电气与自动化工程学院，南昌330013；2.厦门轨道交通集团有限公司，厦门361000）

电气化铁路凭借其高速、重载、环保等优势，从20世纪初出现至今已得到了普遍的重视与推广[1]。与其他的供电系统类似，牵引供电系统中也存在着大量的电能质量问题，其中负序、谐波和无功等问题尤为突出[2-3]。20世纪90年代末期，日本学者提出了铁路功率调节器RPC（railway power conditioner）的概念，并在电气化铁路中投入使用，这种传统RPC采用多个晶闸管串联的形式，其存在着耐压等级低、开关器件数量多和制造成本高等缺陷，使其无法大规模投入使用[4]。

2003年，德国学者Marquart等提出了模块化多电平换流器 MMC（modular multilevel converter）的概念，它具有传统换流器无可比拟的优势[5,6]。文献[7-9]中采用单相模块化多电平换流器SPH-MMC（singlephase modular multilevel converter）作为RPC的换流器，使用这种结构的RPC相对于传统的RPC具有耐压等级高、补偿容量大、开关频率低等优点。

为使RPC达到有效治理牵引供电系统中电能质量的效果，对其控制方式的选取尤为重要。文献[10]采用双闭环PI控制的方式，达到了消除负序、平衡功率的效果；文献[11]通过序列二次规划法SQP（sequential quadratic programming）算法，对所需的补偿电流进行了精确计算，把所得电流期望值引入控制系统，有效地消除了负序电流；文献 [8]对MMC-RPC采用直接功率控制的方式，从功率角度对线路中的电能质量进行治理，并达到了快速精准的效果。但是，由于在RPC与供电臂间的传输线路中电阻与电感会产生额外的损耗，这种损耗使RPC输入到牵引网中的电能与期望值产生偏差无法精确的进行补偿。以上文献所提的控制方式均未考虑到传输线路的损耗对RPC治理效果的影响。

文献[12,13]提出了下垂控制的概念，这种控制方式模拟发电机中的下垂曲线。通过设计有功功率P-频率f、无功功率Q-电压幅值U之间的关系达到控制并稳定电压幅值、频率的效果。由此，本文对MMC-RPC引入下垂控制，设计了MMC-RPC的P-f、Q-U下垂控制系统。同时，考虑传输线路上的阻感影响，推导出系统输出有功、无功功率的耦合关系，设计了一种改进型的下垂控制系统，此控制系统可降低对线路参数的敏感度，更为有效地跟踪参考功率，同时也可维持换流器输出的电压与频率更加稳定，进一步提升牵引供电系统的电能质量。

1 MMC-RPC建模及其等效电路

图1为MMC-RPC及一段牵引线路的结构示意。图中，牵引变电所将公共电网上220 kV/110 kV的三相交流电变为牵引网上27.5 kV的单相交流电，变电所副边所连接的左右两个供电臂用j=R,L表示。左右两侧SPH-MMC背靠背连接成MMC-RPC，分别并联在左右供电臂上，由于MMC优越的耐压特性，可无需降压变压器直接与供电臂相连[10,14]。供电臂上的电压、电流分别为uj、iwj，从j侧供电臂流入RPC的电流为 ijk，k=a、b表示 SPH-MMC的两相桥臂，每个SPH-MMC中包含4N个子模块SM（submodule）右上角虚线框内为其结构示意。

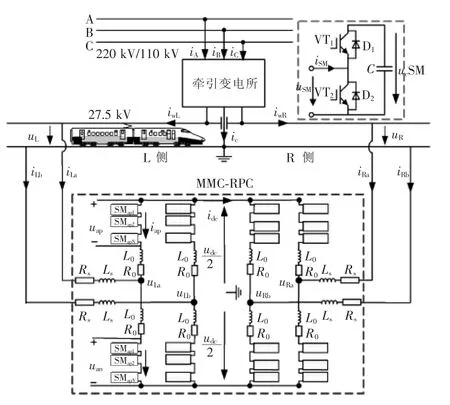
图1 MMC-RPC拓扑结构Fig.1 Topological structure of MMC-RPC

图1中，j侧SPH-MMC的k相上桥臂N个子模块的电压和为ujkp，流过其电流为ijkp；下桥臂的电压和为 ujkn，电流为 ijkn；中间直流环节电压为 udc，Rs、Ls为传输线路上的电阻与电感，R0、L0为桥臂上的电阻与电感。

由于供电臂上的电压基本上维持衡定，故可近似等效为一个电压源，MMC-RPC左右两个SPHMMC可看作两个受控电压源，由此可构建出MMCRPC的等效受控电压源模型，如图2所示。

图2中，uj表示供电臂上的电压矢量，ij表示流入/出 SPH-MMC的电流矢量，uja、ujb为传输线路与SPH-MM中a、b相桥臂连接点的电压矢量，uspj=ujaujb表示SPH-MMC输出端口的电压矢量。其中，传输线路阻抗，阻抗角，阻抗向量 Zs=Zs∠φs。令 uj=Uj∠φj、uspj=Uspj∠φspj， 其中φspj和φj分别为j侧SPH-MMC端口电压相位角与j侧供电臂电压相位角；Uj、Uspj为供电臂上电压幅值和输出端口电压幅值。由基尔霍夫电压定律，对于SPH-MMC的交流侧，有

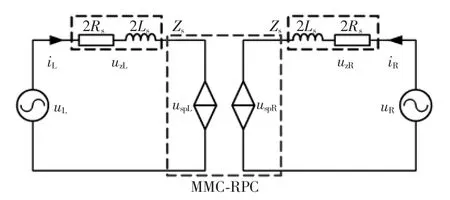
图2 MMC-RPC受控电压源等效模型Fig.2 Equivalent controlled voltage source model of MMC-RPC

对于SPH-MMC的直流侧，有

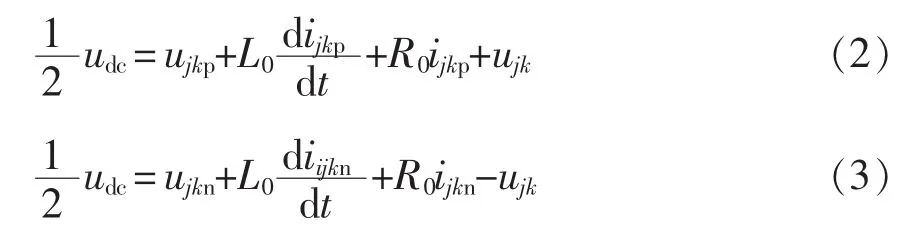
式（2）、式（3）相加，可得到 SPH-MMC 直流侧的数学模型为

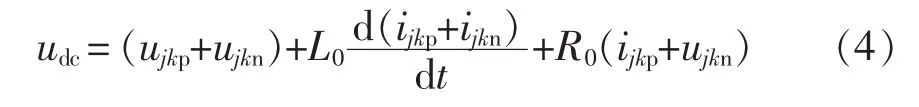
式（2）与式（3）相减，可得到 SPH-MMC 内部的数学模型为

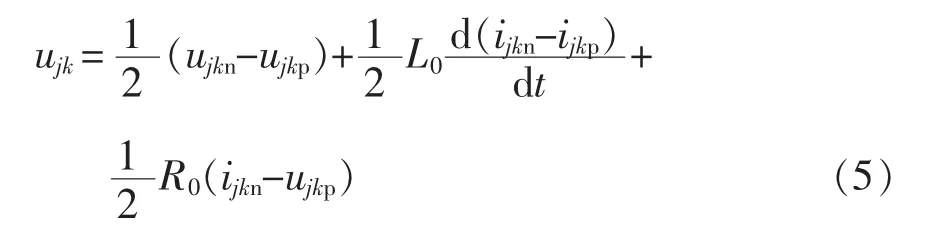
由SPH-MMC内部数学模型可知，通过合理的控制方式来安排SPH-MMC桥臂上子模块的投切可控制 ujkp、 ujkn、ijkp、ijkn进 而调控 RPC 输端电压与电流，使其发挥治理牵引供电系统电能质量的作用。

2MMC-RPC的P-f/Q-U下垂控制原理

下垂控制模仿电机的控制方式，通过构造换流器输出的有功功率、无功功率与输出的电压幅值、频率之间的关系来设计其期望的输出电压[15-16]。

通过式（1）可求得SPH-MMC输出电流矢量为

RPC中其中一侧SHP-MMC向供电臂输出的复功率为

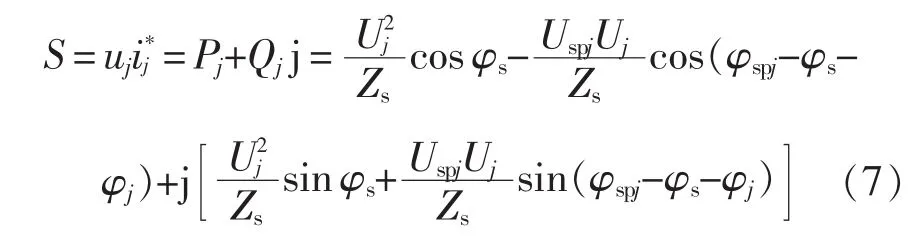
故有

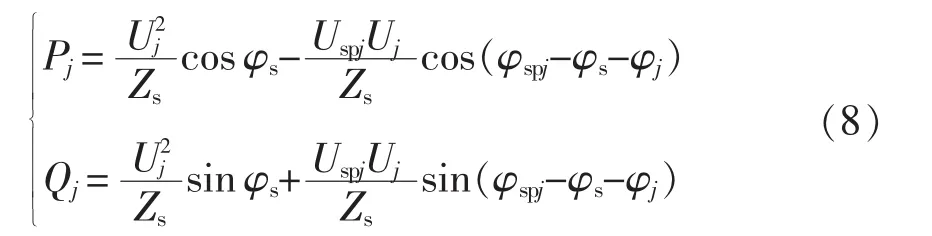
当SPH-MMC与供电臂线路连接线上的阻抗近似为感性，即 φs≈90°时，则式（8）可以化简为

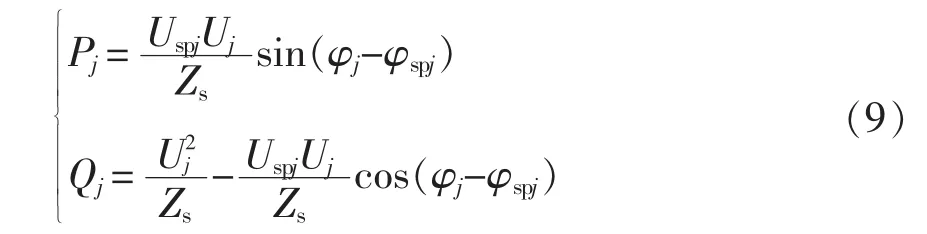
对有功功率、无功功率分别求换流器输出电压幅值Uspj、相位角φspj的偏微分，可得

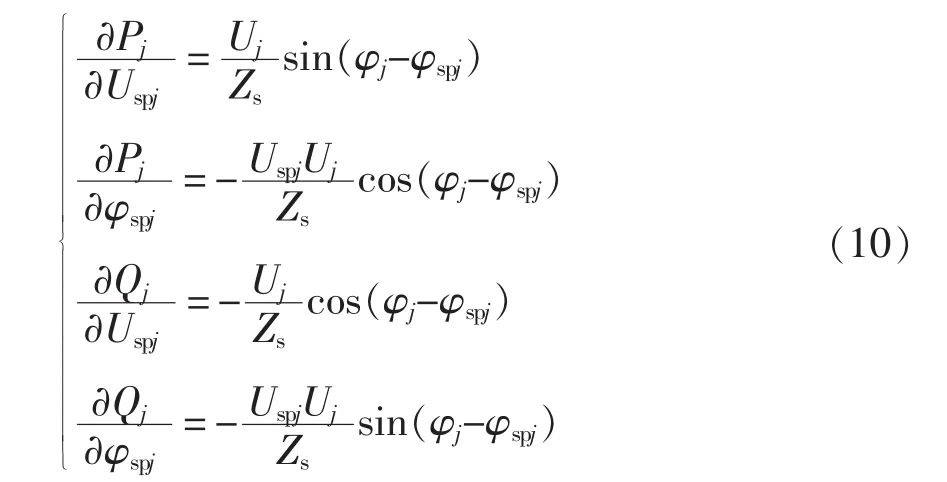
由于在实际中，传输线路上阻抗Zs上的电压uzj（uzj=Zsij）相对于换流器输出端口电压与供电臂上电压数值非常小，又由于uj=uzj+uspj故可近似认为φj-φspj≈0 ，由此可将式（10）进一步化简为

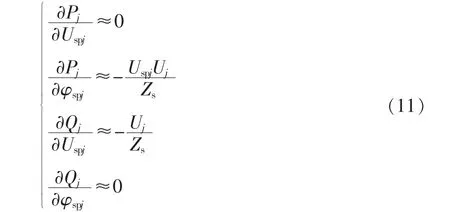
从式（11）可知，电压相位角φspj的变化对于有功功率的影响较大，电压幅值Uspj的变化对于无功功率的影响较大。由此可以通过调控电压相位角对输出有功功率进行控制，控制电压幅值来控制无功功率，由于相位角φspj不便于检测，常用角频率ωspj替代[17]。控制方程为

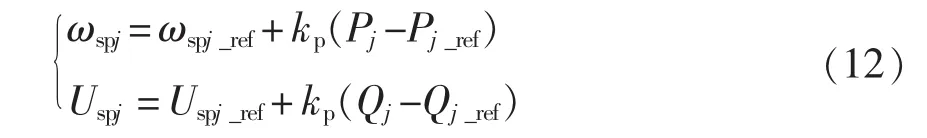
式中，ωspj_ref、Uspj_ref、Pj_ref、Qj_ref分别为 SPH-MMC 期 望的输出电压角频率、幅值以及有功功率、无功功率，kp、kq为下垂控制系数。图3为这种传统下垂控制的控制框图（L侧SPH-MMC）

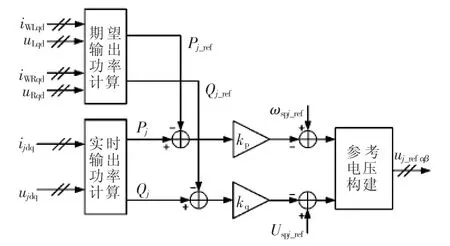
图3 L侧SPH-MMC传统下垂控制框图Fig.3 Block diagram of traditional droop control of SPH-MMC on L side

3 改进型P-f/Q-U下垂控制

由于RPC与牵引网的连接线路上的阻抗往往不呈纯感性，并且线路阻抗的存在也会对RPC的补偿量造成一定的偏差，同时，左右两侧的传输线上的阻感参数可能出现不相等的现象。为此，设计一种改进型的下垂控制策略，使得传输线路对RPC治理效果的影响最小化，并提升控制性能。

设RPC其中一侧SPH-MMC输出端口的电压uspj=Uspj∠0，即 φspj=0。将其代入式（8）中，可得

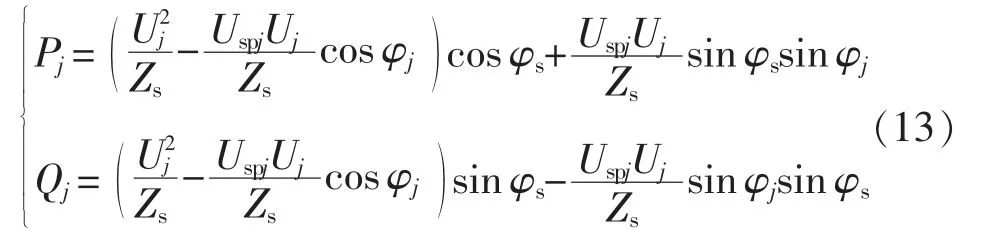
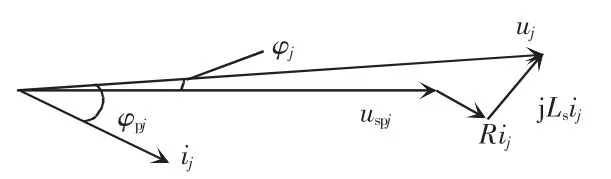
图4 SPH-MMC交流侧向量Fig.4 Vectors of SPH-MMC on AC-side

SPH-MMC交流侧向量如图4所示，其中，φpj为j侧供电臂的功率因数角。

在向量图中，因为 φspj=0，可知 φj→0，则 sin φj≈0、cosφj≈1。令

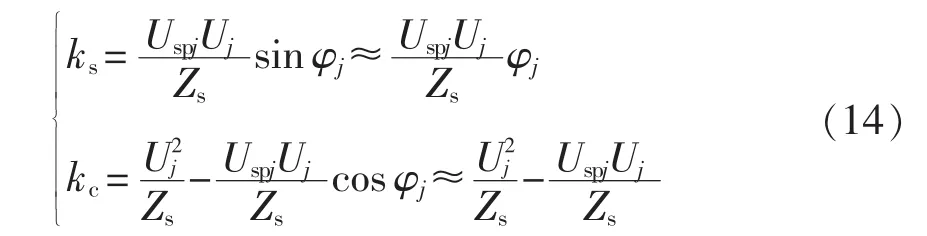
代入式（13），可以得到有功功率、无功功率的另一种表达方式为

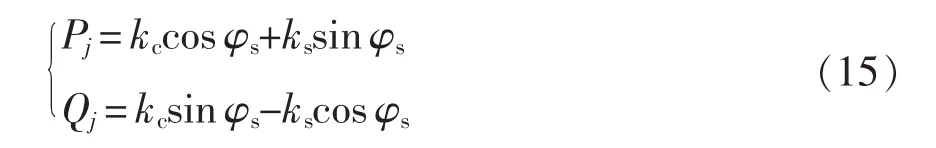
由传输线路上的阻抗角对应关系可知sin φs=，由此可以得到ks、kc的矩阵表达式

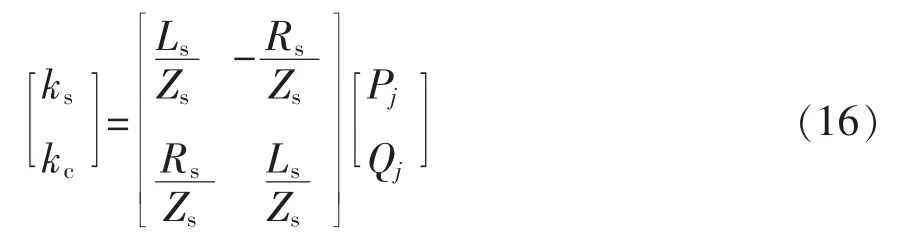
把式（14）代入式（16），进一步推导可以得到

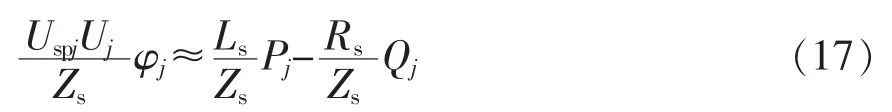
进一步变换可得

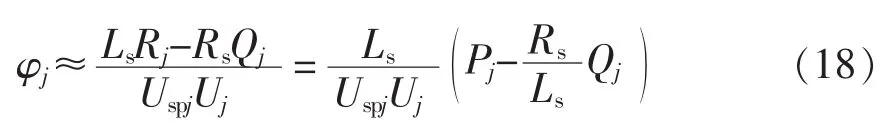
同样情况，有

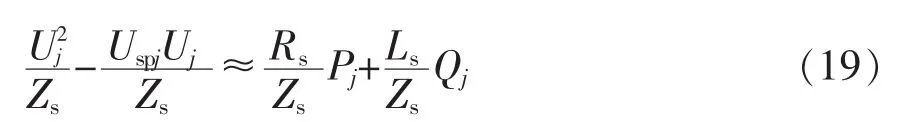
进一步变换有

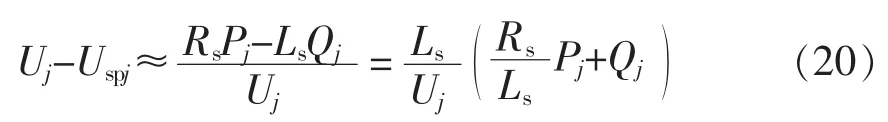
可见，RPC系统期望输出电压的相位角及其幅值由有功功率与无功功率相互耦合计算得来。由此可以推导出采用功率解耦并结合阻感比的改进型下垂控制方程为

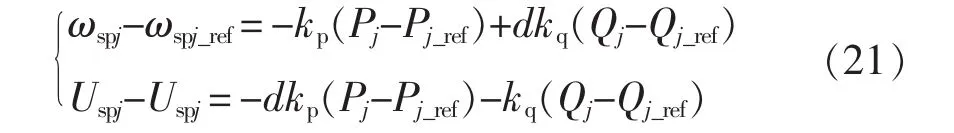
式中，d为传输线路的阻感比，。值得注意的是，当左右两侧传输线路上的阻感参数不相等时，则此左右两侧SPH-MMC控制器中的阻感比分别为dL、dR分别对应左右两侧的电阻与电感之比。由于我国的牵引供电系统采用50 Hz、有效值为27.5 kV的单相交流电，故参考电压幅值Uspj_ref=27.5×，角频率 ωspj_ref=2πf=100π rad/s。图5为改进型SPH-MMC下垂控制的结构框图。

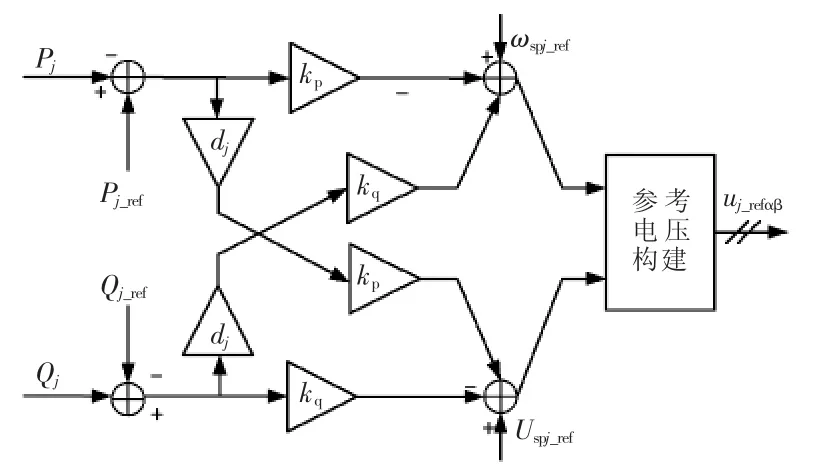
图5 改进型SPH-MMC下垂控制框图Fig.5 Block diagram of improved droop control of SPH-MMC

4 控制器的设计

本文采用电压、电流双环的方式对RPC进行控制，其中，电压环控制SPH-MMC的期望输出电流，其输入参考电压由下垂控制环节产生，电流环控制SPH-MMC交流侧节点电压，其输入参考电流由电压环产生。最后由式（2）、式（3）、式（5）并通过电容电压排序算法来控制桥臂上子模块的投切[18]，进而控制MMC-RPC的输出。

4.1 电压环的设计

由SPH-MMC交流侧数学模型并经过坐标变换可知，换流器输出的电压、电流间存在积分与耦合的关系。若使下垂控制所产生的参考电压变换到dq旋转坐标轴上，再通过使用比例积分PI（proportional integral）环节的电压环，这种控制系统存在稳态误差大、相应速度慢的缺点。文献[19]提出了一种采用比例复数积分PCI（proportional complex integral）策略的控制器，它能有效地消除稳态误差，无需dq变换，加快了系统反应速度。本文电压环采用PCI控制器，其结构框图如图6所示，其传递函数[20]为

式中：kp、kci为比例系数与复数积分系数；ω0为谐振角频率，ω0=2πf=2π×50=100π rad/s。

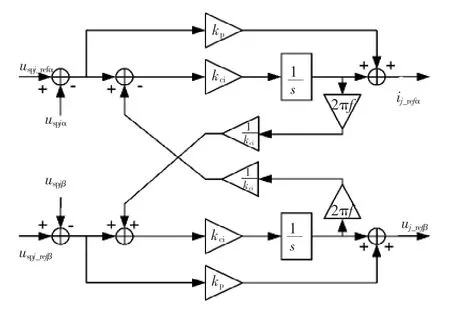
图6 电压环PCI控制器框图Fig.6 Block diagram of voltage loop PCI controller

4.2 电流环的设计

考虑到比例积分控制器具有动态响应快、结构简单、设计方便的优点，电流环采用较为常见的比例积分控制器，其主要功能在于平衡两侧供电臂电流，进而消除三相电网中的负序电流以及降低负载不对称的影响，增强系统鲁棒性[21,22]。图7为电流环PI控制器的结构框图。由于PI控制器对于非直流量不具有零稳态误差控制的效果[20]，故先采用dq变换模块把输入电流变换为dq旋转坐标上的直流量。

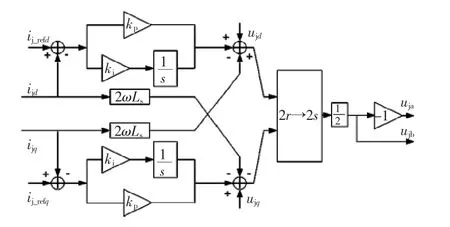
图7 电流环PI控制器框图Fig.7 Block diagram of current loop PI controller

4.3 整体控制器

把上述下垂控制环节和电压电流环等控制环节有机结合起来，即可构成对MMC-RPC的整体控制器，其结构简图如图8所示。

其中，电容电压排序算法根据SPH-MMC桥臂上电流的正负对子模块电容电压进行升/降排序，决定SPH-MMC桥臂上所投入的子模块，进而控制SPH-MMC的输出电压。

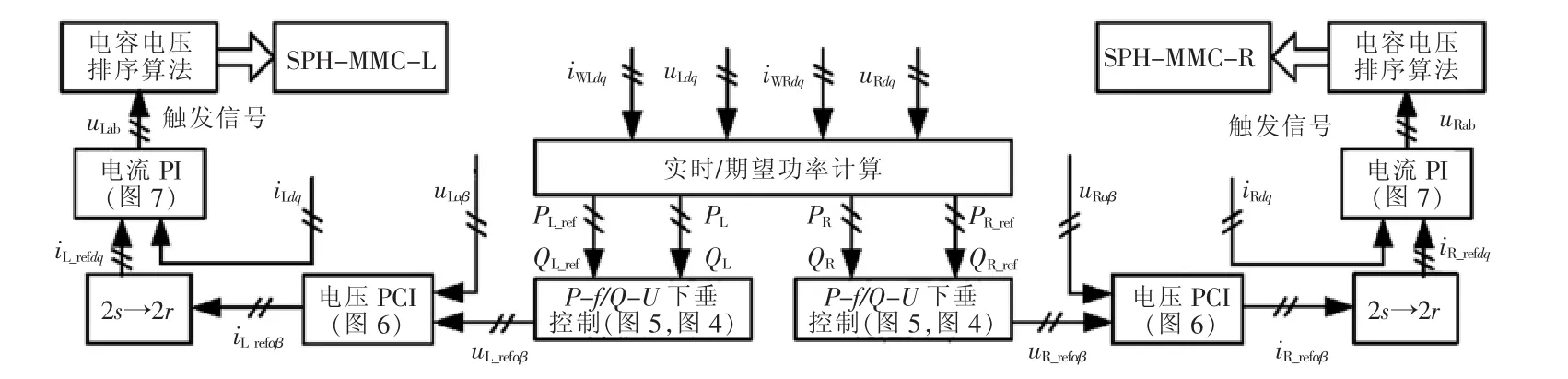
图8 整体控制框图Fig.8 Block diagram of overall control

5 仿真分析

为验证所提下垂控制应用于MMC-RPC的有效性与优越性，在MATLAB/Simulink环境中模拟一种较严重的牵引线路负载不平衡现象进行仿真。仿真模型中，R侧供电臂上带有有功功率为8 MW、无功功率为0.5 Mvar的机车负载，L侧供电臂上暂无受电弓接触。表1为仿真系统的基本参数。

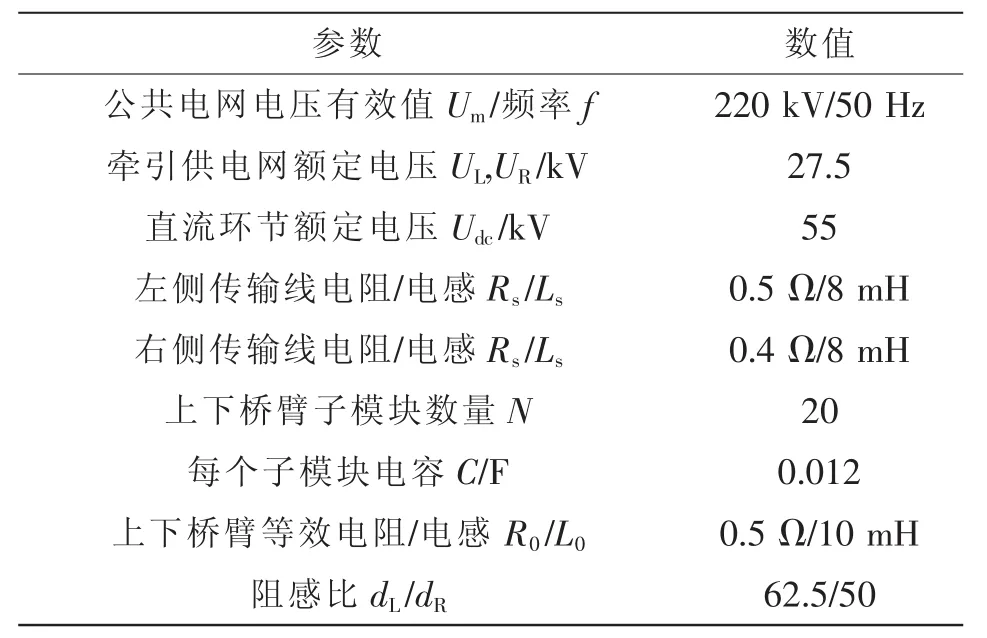
表1 仿真参数Tab.1 Simulation parameters

5.1 控制性能对比

图9为采用传统P-f/Q-U下垂控制与改进型下垂控制两种控制方式下MMC-RPC对牵引供电系统治理前后左右两侧供电臂上的有功功率与无功功率变化曲线。从图中可以看出，MMC-RPC治理前后由于改进型下垂控制考虑了传输线路上的阻抗损耗，在控制系统中引入了阻感比及功率耦合，在其控制下MMC-RPC所连接的两侧供电臂上的功率相比于传统下垂控制方式更趋近于相等。图10为两种下垂控制方式下角频率与电压幅值的对比波形。

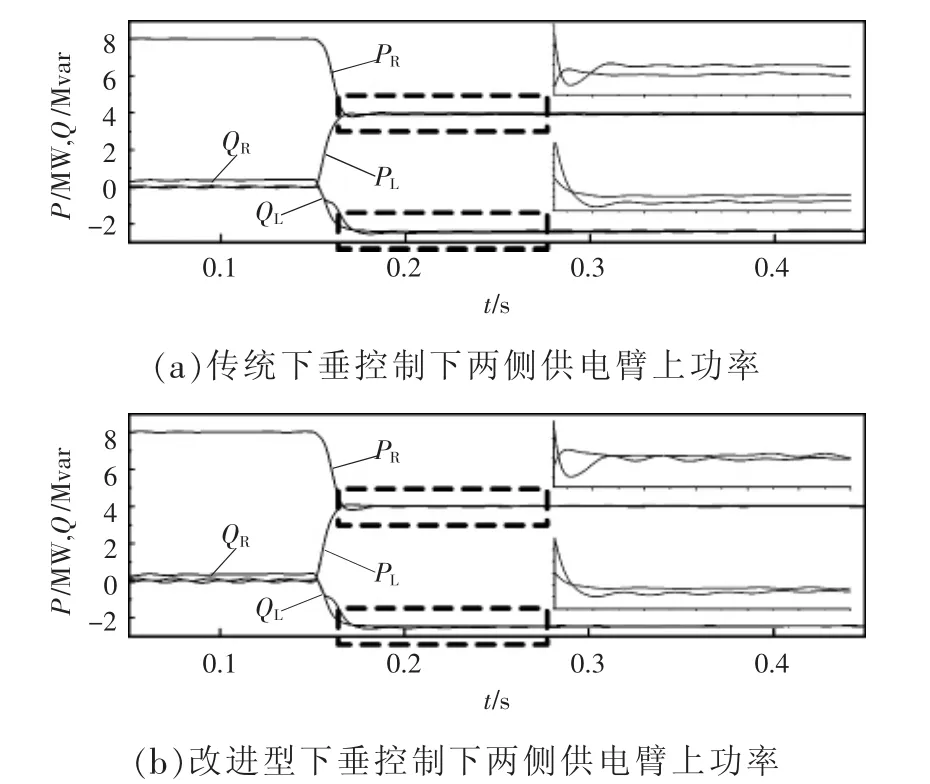
图9 MMC-RPC投入前后功率对比Fig.9 Power comparison before and after deployment of MMC-RPC

从图10中可以观察到，改进型下垂控制所输出的电压角频率及其幅值相对于传统P-f/Q-U下垂控制输出波形更为稳定。由此验证了改进型下垂控制具有更好的控制性能。

5.2 改进型下垂控制对于负序电流的治理效果

由于左右两侧供电臂上所带的负载不平衡，两侧的电流也相差迥异，图11为在改进型下垂控制下，MMC-RPC投入前后左右两侧供电臂上的电流波形，以及牵引变电所原边三相供电系统中的电流波形。

从图11可知，在MMC-RPC投入使用之前，R、L两侧供电臂上的电流不平衡，由于L侧上无负载，其电流趋近于0，变电所原边的三相电流不对称，存在大量的负序电流。在0.15 s后，由于MMCRPC的治理作用，L、R侧电流能较快的达到平衡状态，随之原边三相电流也趋于平衡，负序分量得以消除。由此可知这种改进型下垂控制下的MMC-RPC能有效，迅速地使电流达到平衡的状态，进一步验证了这种下垂控制方式的有效性。同时观察0.15 s后短时间内的电流变化过程可得知，这种改进型下垂控制方式具有较快的反应速度与动态性能。

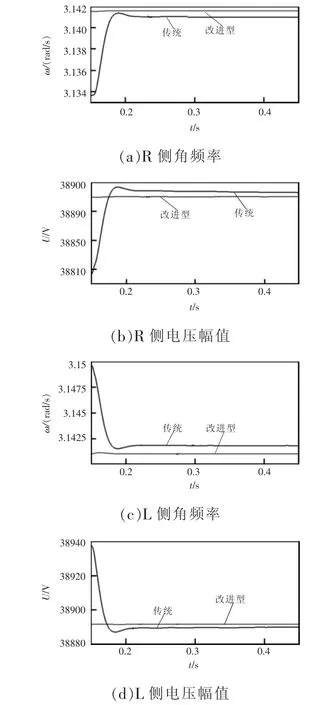
图10 两种下垂控制方式下的输出角频率、电压幅值波形Fig.10 Waveformsofoutputangularfrequency and voltage amplitude in two droop control modes

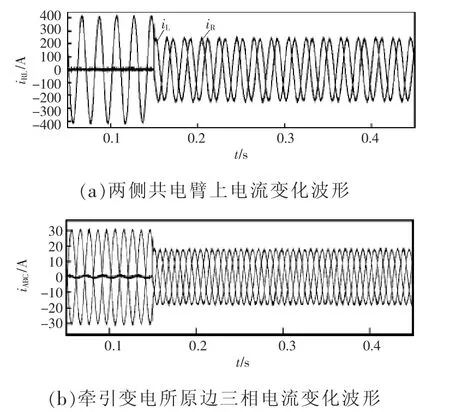
图11 MMC-RPC投入前后电流波形Fig.11 Current waveform before and after the deployment of MMC-RPC

6 结语

本文提出了应用于MMC-RPC的下垂控制方式，并在此基础上考虑传输线路上的阻感影响，提出了一种采用功率耦合与阻感比结合的新型下垂控制方式，它可实现MMC-RPC更为精确有效的治理牵引供电系统中的电能质量。

仿真结果进一步说明了本文所提的新型下垂控制方式相对于传统的P-f/Q-U下垂控制有较为优越的控制性能，其反应速度更快，控制部分输出的频率与电压幅值能更快更平稳地达到期望的稳定状态，MMC-RPC对供电臂两侧的功率治理也能使其两侧功率更趋于平衡。改进型下垂控制作用MMC-RPC能使得两侧供电臂上的电流与变电所原边的三相电流能较快地达到平衡状态，有效地消除负序电流。

[1]Mousavi G S M,Tabakhpour L A,Fuchs E F,et al.Power quality issues in railway electrification:a comprehensive perspective[J].IEEE Transactions on Indu-strial Electronics,2015,62（5）:3081-3090.

[2]Kaleybar H J,Fallah M,Kojabadi H M,et al.A new robust dynamic control method for railway power quality compensator[C].2016 IEEE 8th International Power Electronics and Motion Control Conference（IPEMC-ECCE A-sia）.Hefei,China,2016,8:1345-1349.

[3]Hu Haitao,He Zhengyou,Li Xin,et al.Power-quality impact assessment for high-speed railway associated with high-speed trains using train timetable-Part I:Methodology and modeling[J].IEEE Transactions on Power Delivery,2016,31（2）:693-703.

[4]徐千鸣,马伏军,何志兴,等.双星型多电平铁路功率调节器及其控制方法[J].中国电机工程学报,2016,36（13）:3609-3619.Xu Qianming,Ma Fujun,He Zhixing,et al.A railway power conditioner and its control method based on double star bridge cells[J].Proceedings of the CSEE,2016,36（13）:3609-3619（in Chinese）.

[5]郭高朋,姚良忠,温家良.模块化多电平变流器的子模块分组调制及均压控制[J].中国电机工程学报,2016,36（1）:145-153.Guo Gaopeng,Yao Liangzhong,Wen Jialiang.The grouping modulation and voltage balance control of the submodules in modular multilevel converter[J].Proceedings of the CSEE,2016,36 （1）:145-153（in Chinese）.

[6]董云龙,汪楠楠,田杰,等.一种新型模块化多电平换流器[J].电力系统自动化,2016,40（1）:116-121.Dong Yunlong,Wang Nannan,Tian Jie,et al.A novel modular multilevel converter[J].Automation of Electric Power Systems,2016,40（1）:116-121（in Chinese）.

[7]荆龙,唐芬,王之赫,等.基于模块化多电平换流器的牵引供电系统电能质量治理方法[J].电力系统自动化,2015,39（11）:173-179.Jing Long,Tang Fen,Wang Zhihe,et al.A power quality compensating method for traction power supply system based on MMC[J].Automation of Electric Power Systems,2015,39（11）:173-179（in Chinese）.

[8]宋平岗,林家通,李云丰,等.基于模块化多电平的铁路功率调节器直接功率控制策略[J].电网技术,2015,39（9）:2511-2518.Song Pinggang,Lin Jiatong,Li Yunfeng,et al.Direct power control strategy of railway static power conditioner based on modular multilevel converter[J].Power System Technology,2015,39（9）:2511-2518（in Chinese）.

[9]宋平岗,林家通,李云丰,等.基于模块化多电平换流器的牵引供电负序治理[J].电源学报,2015,13（6）:18-27.Song Pinggang,Lin Jiatong,Li Yunfeng,et al.Negative sequence governance for traction power supply based on modular multilevel converter[J].Journal of Power Supply,2015,13 （6）:18-27.

[10]王卫安,桂卫华.两相牵引供电系统电能质量有源综合治理技术研究[J].铁道学报,2013,35（9）:31-38.Wang Weian,Gui Weihua.Comprehensive active power quality compensation technology for two phase traction power supply system[J].Journal of the China Railway Society,2013,35（9）:31-38（in Chinese）.

[11]Zhang Dinghua,Zhang Zhixue,Wang Weian,et al.Negative sequence current optimizing control based on railway static power conditioner in V/v traction power supply system[J].IEEE Transactions on Power Electronics,2016,31（1）:200-212.

[12]芦思晨,潘再平.无储能风电微网系统的下垂控制策略[J].电工技术学报,2016,31（18）:169-175.Lu Sichen,Pan Zaiping.Droop control strategy of wind power microgrid system without energy storage device[J].Transactions of China Electrotechnical Society,2016,31（18）:169-175（in Chinese）.

[13]Liu Ming'ao,Zhao Bing,Chen Jie.Research on circulating current reduction of droop-controlled parallel inverters[J].IEEE,Power Electronics and Applications（EPE'16 ECCE Europe）,2016,18:1-10.

[14]Khamphakdi P,Sekiguchi K,Hagiwara M,et al.A transformerless Back-To-Back（BTB） system using modular multilevel cascade converters for power distribution systems[J].IEEE Transactions on Power Electronics,2015,30（4）:1866-1875.

[15]Xin Huanhai,Huang Linbin,Zhang Leiqi,et al.Synchronous instability mechanism of P-f Droop-Controlled voltage source converter caused by current saturation[J].IEEE Transactions on Power Systems,2016,31（6）:5206-5207.

[16]冉晓洪,苗世洪,吴英杰,等.基于最优功率分配的多端直流网络改进下垂控制策略[J].电工技术学报,2016,31（9）:16-24.Ran Xiaohong,Miao Shihong,Wu Yingjie,et al.An improved droop control strategy for multi-terminal DC grids based on optimal active power allocation[J].Transactions of China Electrotechnical Society,2016,31（9）:16-24（in Chinese）.

[17]彭春华,王立娜,李云丰.低压微电网三相逆变器功率耦合下垂控制策略[J].电力自动化设备,2014,34（3）:28-33.Peng Chunhua,Wang Lina,Li Yunfeng.Strategy of powercoupling droop control for three-phase inverter in lowvoltage microgrid[J].Electric Power Automation Equipment,2014,34（3）:28-33（in Chinese）.

[18]郭裕群,赵成勇,许建中,等.模块化多电平换流器子模块平均开关频率的精确控制方法[J].电力系统自动化,2016,40（19）:94-100.Guo Yuqun,Zhao Chengyong,Xu Jianzhong,et al.Precision control method of average sub-module switching frequency for modular multilevel converters[J].Autonation of Electric Power Systems,2016,40（19）:94-100（in Chinese）.

[19]郭小强.光伏并网逆变器通用比例复数积分控制策略[J].中国电机工程学报,2015,35（13）:3393-3399.Guo Xiaoqiang.Generalized proportional complex integral control scheme for PV grid-connected Inverters[J].Proceedings of the CSEE,2015,35（13）:3393-3399（in Chinese）.

[20]Yang Qiuxia,Xu Jinling,Gao Rui.Research on control strategy for single-phase grid-connected inverter based on proportional complex integral control[J].Intelligent Human-Machine Systems and Cybernetics（IHMSC）,2010,2:26-28.

[21]Jagatheesan K,Anand B,Dey N,et al.Automatic generation control of an interconnected multi-area reheat thermal power systems with conventional proportional-integral controller considering various performance indices[J].IEEE International Symposium on Applied Computational Intelligence and Informatics,2016,11:289-294.

[22]冯全源,严宏举.一种变参数比例积分控制BUCK变换器设计[J].电机与控制学报,2016,20（5）:68-76.Feng Quanyuan,Yan Hongju.Design of variable parameter proportional integral controlled BUCK converter[J].Electri c Machines and Control,2016,20（5）:68-76（in Chinese）.