三电平直流变换器混杂系统建模与控制

杨国润，肖 飞，范学鑫，王瑞田，刘计龙

（海军工程大学舰船综合电力技术国防科技重点实验室，武汉430033）

直流变换器的建模与控制一直是电力电子方向研究人员关注的重点[1-3]。与其他电力电子系统一样，直流变换器是高度非线性、变结构的系统。最常用的方法是用状态空间平均法[4]建立稳态工作点附近的小信号模型，在s域中进行控制器设计。这样设计的控制器虽然在稳态工作点附近能够稳定运行，但当系统出现大扰动时动态性能较差，同时，状态空间平均模型还丢失了状态变量的高频响应。

现代控制理论的发展给直流变换器的控制带来了新的变化，诸如滑模控制[5]、鲁棒控制[6]、线性二次型调节器控制[7]、模糊控制[8]和最优控制[9]等相继应用于直流变换器中。但这些应用都有一定的局限性，有些控制方法需针对电流连续模式CCM（continuous current mode）和电流断续模式DCM（discontinuous current mode）建立不同的模型，有些控制方法甚至忽略了DCM模式。直流变换器在全工况范围内通常都包含CCM和DCM两种工作模式，因此需要一种能够在全工况范围内统一的建模方法。

文献[10]将混杂系统建模方法引入了boost变换器，将boost变换器建模成一个混杂自动机，为直流变换器统一建模提供了一种新思路和新方法。所谓混杂系统，就是指同时存在相互作用的连续动态特性和离散事件特性的系统，由此可见直流变换器是一个典型的混杂系统[11]。文献[12-13]基于混杂自动模型分别设计了buck变换器和boost变换器的闭环控制策略，实现了系统的稳定运行。

在三电平直流变换器中，因其三电平拓扑结构可使功率器件的电压应力降至输入电压的一半，广泛应用于高压输入场合[14]。本文将建立三电平直流变换器混杂自动机模型，并设计其闭环控制策略。

1 三电平直流变换器混杂自动机模型

三电平直流变换器的电路如图1所示，中压直流电能在高压侧经二极管箝位三电平全桥逆变电路逆变后成为脉宽可控的双极性五电平方波，再经单相中频隔离变压器降压后输入到单相不控整流桥，经过LC滤波器滤波后获得低压直流电能。在如图2所示的移相脉宽调制PWM（pulse width modulation）控制下，三电平直流变换器呈现出多种工作模态，每一种工作模态对应着一个离散状态，而工作模态之间的相互切换又可以用连续状态来表示。

三电平直流变换器的混杂自动机模型如下。设X=x1，x2，…，xn是系统连续状态变量 xi（i=1,2,…，n）的有限集，S=s1，s2，…，sn是系统的离散状态 si（i=1,2,…，n）的有限集，对应系统不同的工作模态，则对于任意一个s，系统的状态方程可以表示为

其中：x∈X；As∈Rn×n；Bs∈Rn×1。

混杂自动机模型可以表示为 H=（X，S，f，E，F，init，∑），其中，f为系统的状态方程，E 为可能的切换集合，F为切换条件，init为初始条件，∑为系统事件。状态切换一次即发生一次事件，混杂自动机模型如图3所示。从图3中可以看出，离散状态的切换取决于系统的连续状态变量，同时离散状态的切换又会导致连续状态变量的变化，两者之间相互耦合、相互影响，构成了一个典型的混杂自动机模型。

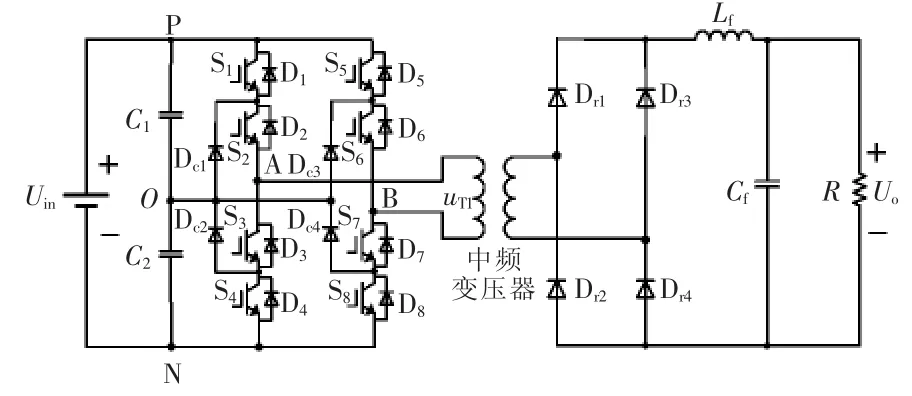
图1 三电平直流变换器拓扑结构Fig.1 Topology of three-level DC-DC converter

图2 移相PWM原理Fig.2 Principle of phase-shifted PWM

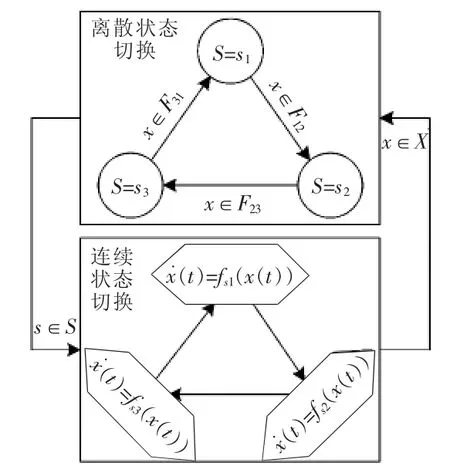
图3 混杂自动机模型Fig.3 Hybrid automaton model

混杂自动机模型的关键是确定离散状态之间的切换条件，切换条件决定系统在每一个离散状态停留的时间，基于切换条件可实现系统闭环控制。

三电平直流变换器有8个全控型功率器件，在移相PWM的控制下，根据不同的负载程度，系统可以划分为4种工作模式，分别是CCM模式、DCM1模式、DCM2模式和DCM3模式。每一种工作模式都包含了多种离散状态，定义系统的连续状态变量的有限集为X=[iLuo]，其中iL为滤波电感电流，uo为输出电压。系统的输入电压为Uin，中频隔离变压器的变比为KT，滤波电感为Lf，滤波电容为Cf，负载电阻为R。

2 三电平直流变换器闭环控制设计

三电平直流变换器的闭环控制可以等效为4种工作模式的切换和每种工作模式中各个工作模态的切换。离散状态的切换取决于状态变量的变化，状态变量的变化又基于离散状态。闭环控制的核心是确定离散状态之间的切换条件，使系统的状态切换轨迹周期性地变化并满足输出电压调节约束。闭环控制稳定的特征是周期固定和输出电压维持在参考值，考虑到三电平直流变换器有4种工作模式，分别进行分析。

2.1 CCM

三电平直流变换器工作在CCM时，电感电流和输出电压的波形如图4所示，每种离散状态对应的状态方程系统矩阵如表1所示。

由图4可知，s1切换至s2的条件为

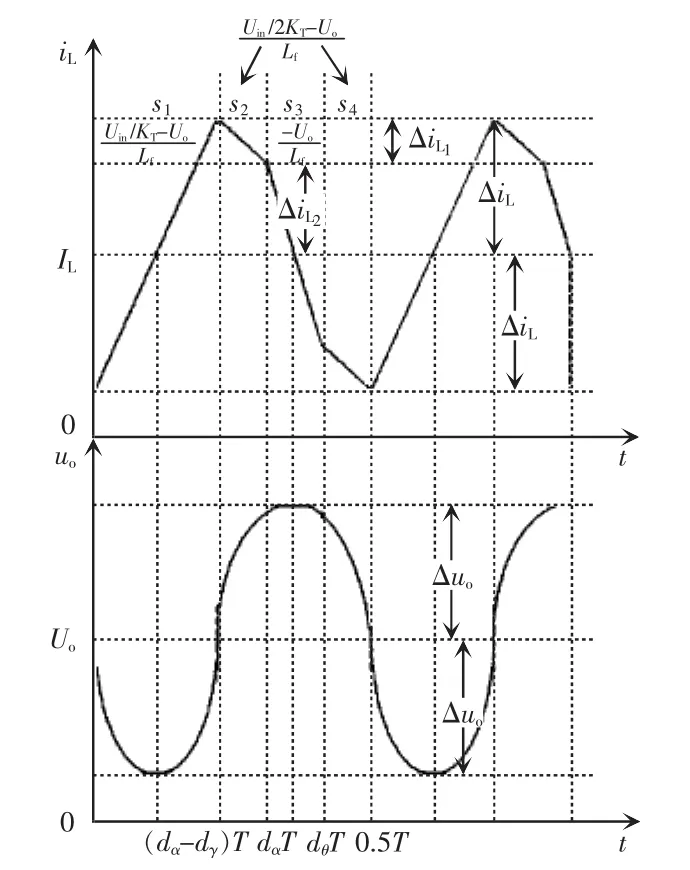
图4 CCM电感电流和输出电压理论波形Fig.4 Theoretical waveforms of inductor current and output voltage in CCM

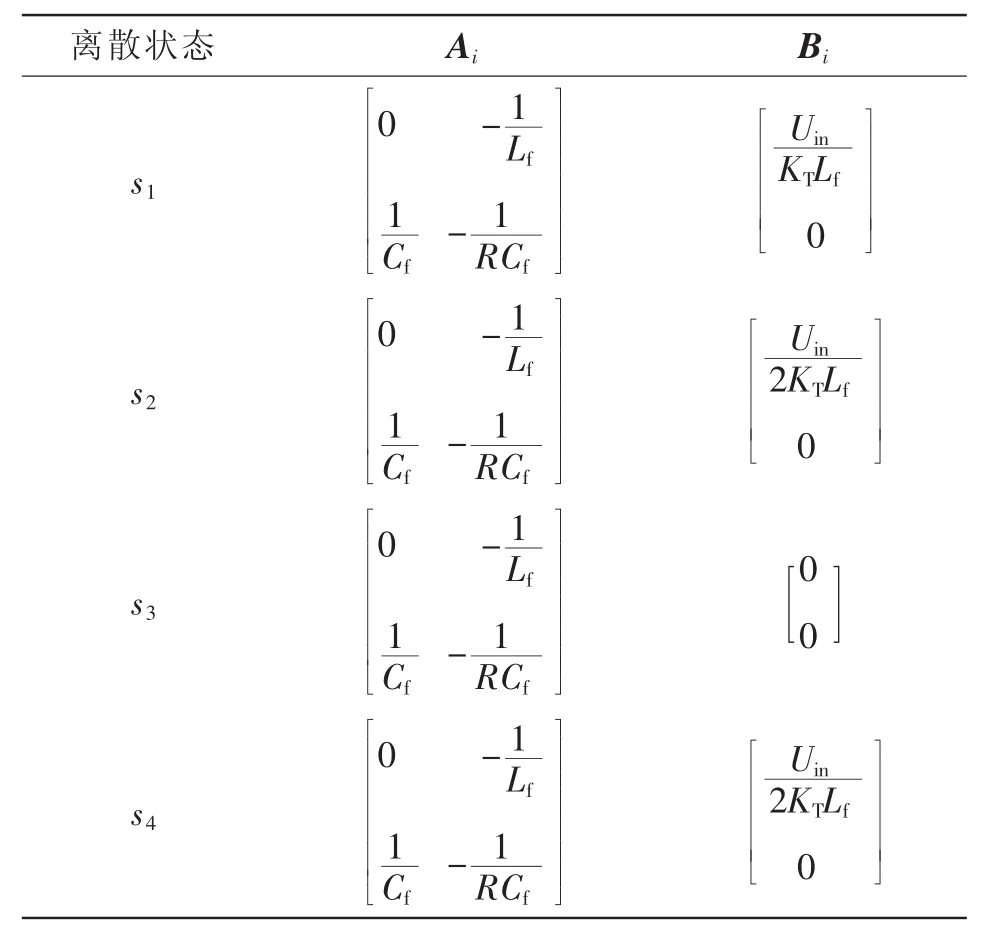
表1 CCM时不同离散状态的系统矩阵Tab.1 System matrices under different discrete states in CCM

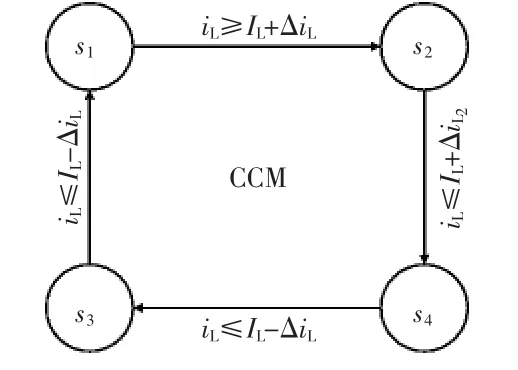
图5 CCM时离散状态转换过程Fig.5 Transition of discrete states in CCM

s2切换至s3的条件为

s3切换至s4的条件为

s4切换至s1的条件为

式中：IL为电感电流平均值；ΔiL为电感电流峰峰值的一半；ΔL2为s2与s3交界处电感电流与其平均值的差。CCM时，离散状态切换过程如图5所示。

2.2 DCM1

三电平直流变换器工作在DCM1时电感电流和输出电压的波形如图6所示，每种离散状态对应的状态方程系统矩阵如表2所示。

由图6可知，s1切换至s2的条件为

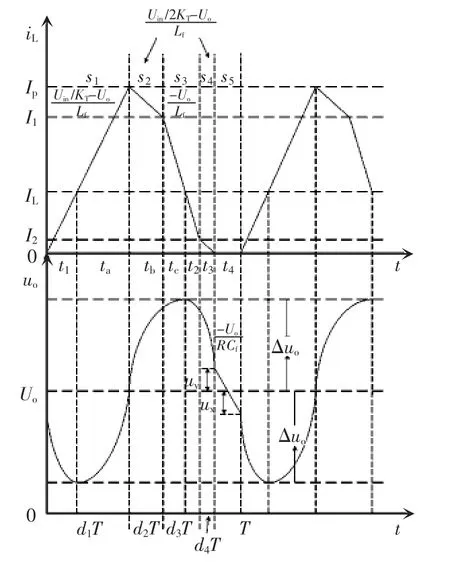
图6 DCM1模式电感电流和输出电压理论波形Fig.6 Theoretical waveforms of inductor current and output voltage in DCM1

表2 DCM1时不同离散状态的系统矩阵Tab.2 System matrices under different discrete states in DCM1

s2切换至s3的条件为

s3切换至s4的条件为

s4切换至s5的条件为

s5切换至s1的条件为

式中：Ip为电感电流峰值；I1为s2与s3交界处电感电流；I2为s3与s4交界处电感电流；ux51为输出电压平均值与s5和s1交界处输出电压的差。

DCM1模式时离散状态切换过程如图7所示。

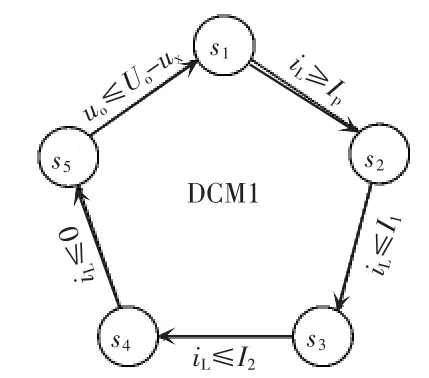
图7 DCM1时离散状态转换过程Fig.7 Transition of discrete states in DCM1

2.3 DCM2

三电平直流变换器工作在DCM2时电感电流和输出电压的波形如图8所示，每种离散状态对应的状态方程系统矩阵如表3所示。

由图8可知，s1切换至s2的条件为

s2切换至s3的条件为

s3切换至s4的条件为

图8 DCM2时电感电流和输出电压理论波形Fig.8 Theoretical waveforms of inductor current and output voltage in DCM2

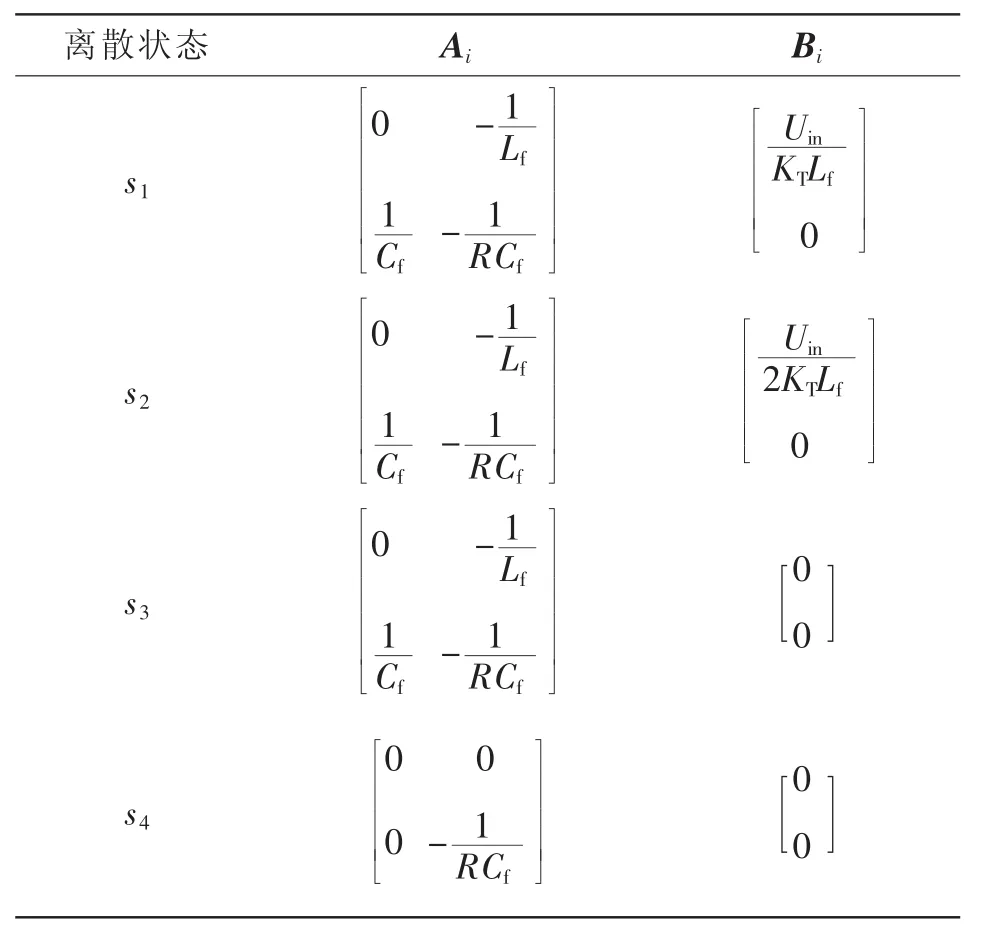
表3 DCM2模式不同离散状态的系统矩阵Tab.3 System matrices under different discrete states in DCM2

s4切换至s1的条件为

式中，ux41为输出电压平均值与s4和s1交界处输出电压的差。

DCM2模式时离散状态切换过程如图9所示。

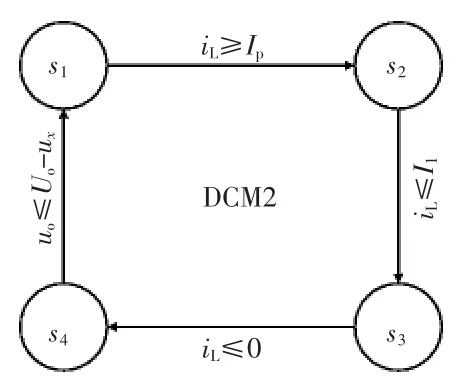
图9 DCM2时离散状态转换过程Fig.9 Transition of discrete states in DCM2

2.4 DCM3

三电平直流变换器工作在DCM3模式时电感电流和输出电压的波形如图10所示，每种离散状态对应的状态方程系统矩阵如表4所示。

由图10可知，s1切换至s2的条件为

s2切换至s3的条件为

s3切换至s1的条件为

式中，ux31为输出电压平均值与s3和s1交界处输出电压的差。

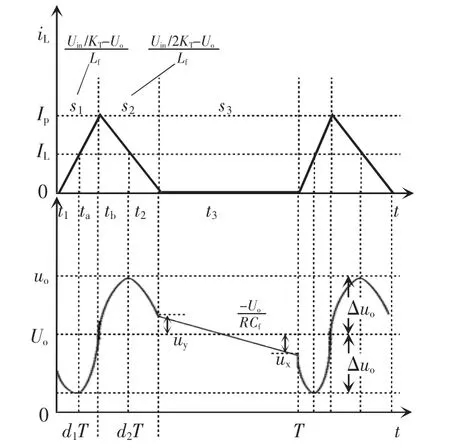
图10 DCM3时电感电流和输出电压理论波形Fig.10 Theoretical waveforms of inductor current and output voltage in DCM3

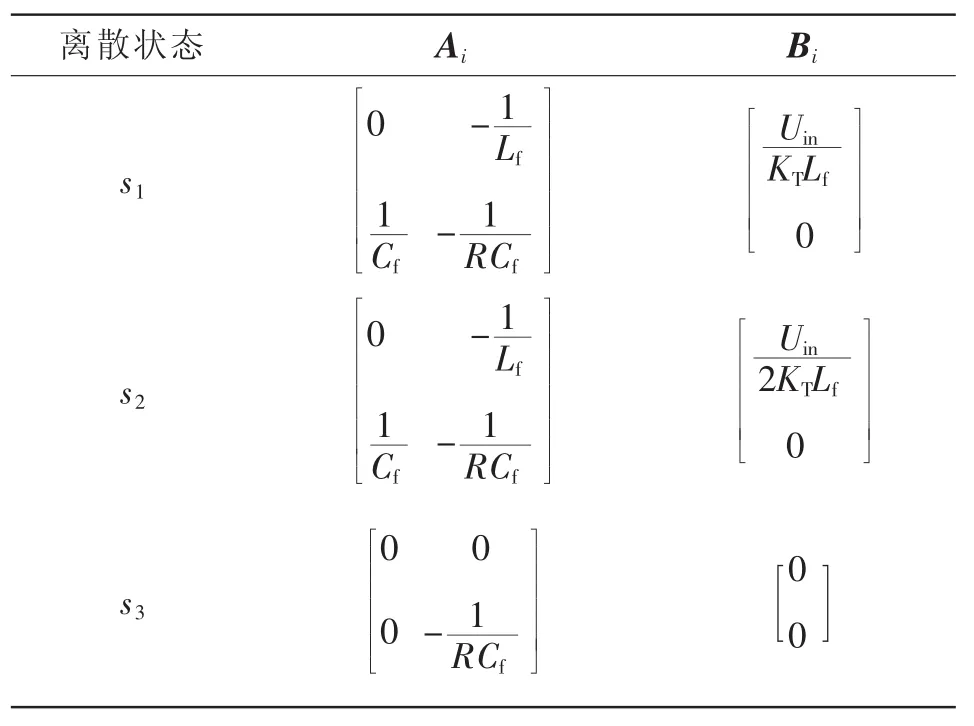
表4 DCM3模式不同离散状态的系统矩阵Tab.4 System matrices under different discrete states in DCM3

DCM3时离散状态切换过程如图11所示。

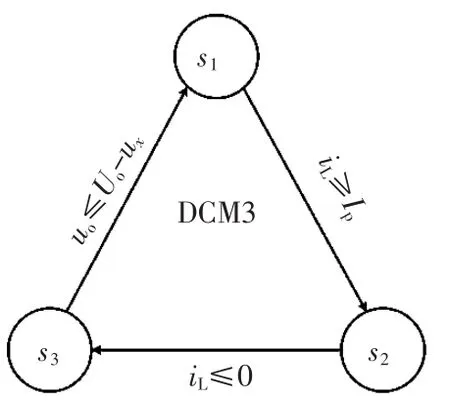
图11 DCM3时离散状态切换过程Fig.11 Transition of discrete states in DCM3

2.5 模式切换

随着负载电阻的增大，移相占空比逐渐减小，移相占空比与负载电阻的关系如图12所示。

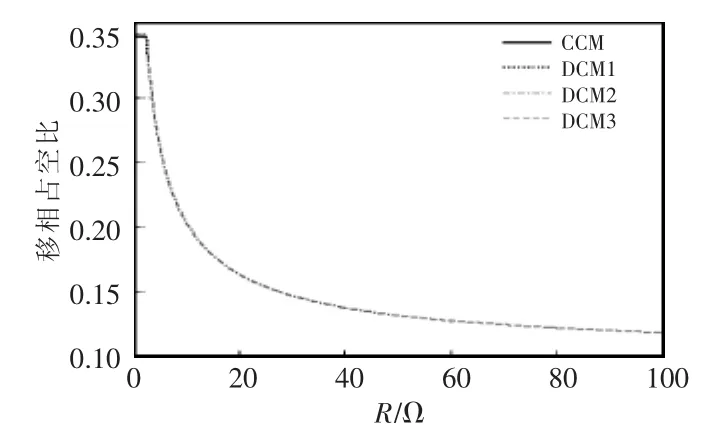
图12 移相占空比与负载电阻的关系曲线Fig.12 Curve of phase-shifted duty cycle versus load resistance

根据前述推导可得，CCM切换至DCM1的条件为

DCM1切换至CCM的条件为

DCM1切换至DCM2的条件为

DCM2切换至DCM1的条件为

DCM2切换至DCM3的条件为

DCM3切换至DCM2的条件为

因此，各模式间的切换过程如图13所示。

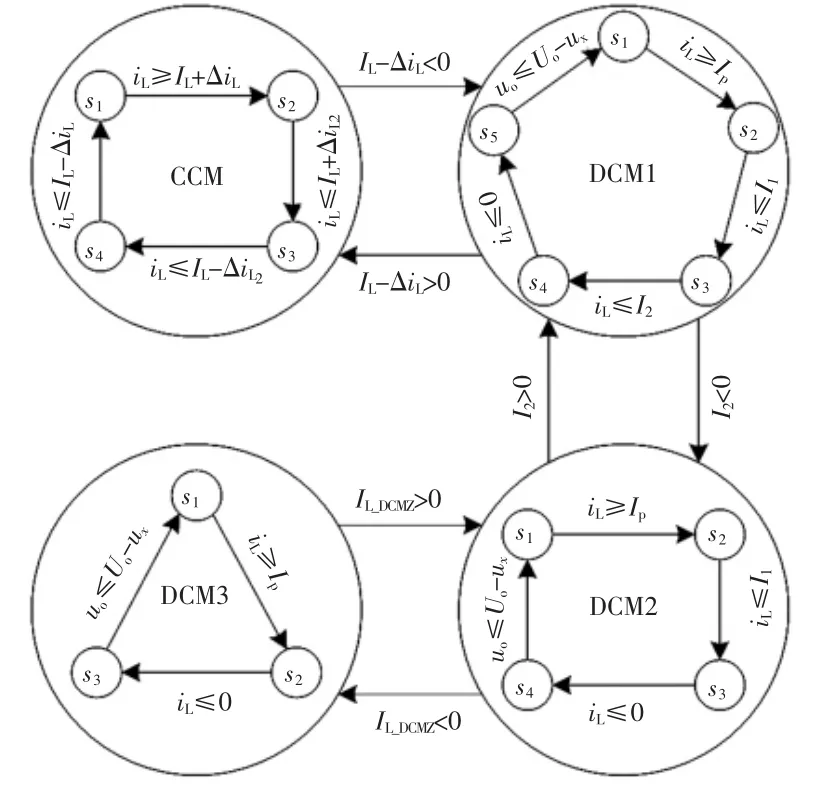
图13 各模式间的转换过程Fig.13 Transition of different modes

3 仿真验证

混杂自动机模型可以借助Matlab/Simulink中的Stateflow工具箱进行仿真研究。在Simulink中分别搭建了三电平直流变换器开环混杂自动机模型和电路模型，模型参数与理论分析时一致，两者仿真结果如图14所示，图形曲线验证了开环混杂自动机模型的可行性和正确性。

为了验证三电平直流变换器闭环控制时离散状态切换条件正确性，同样在Simulink中搭建了仿真模型，模型参数为：Uin=4 000 V，Uo=710 V，Δuo=7 V，Lf=250 μH，Cf=5 mF，KT=3.921 6，CCM 时 R=2 Ω，DCM1时 R=2.667 Ω，DCM2 时 R=3 Ω，DCM3 时R=49.1 Ω。仿真结果分别如图15～图18所示，由图可以看到，仿真结果与理论分析一致，系统进入周期循环稳定工作中。图19～图21为CCM与3种DCM相互切换时暂态过程，从图中可以看出，输出电压表现出了快速的动态响应，且超调小。

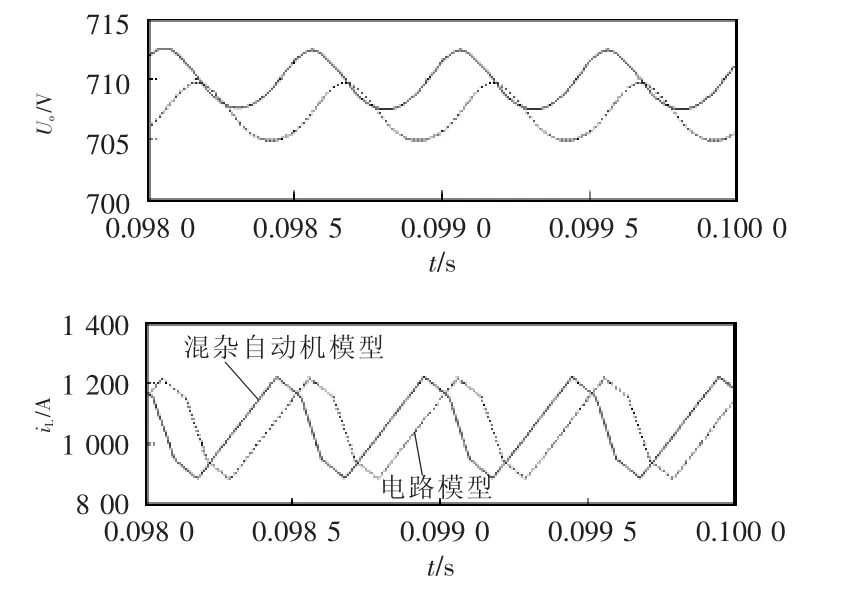
图14 开环输出电压和电感电流仿真波形Fig.14 Simulation waveforms of output voltage and inductor current in open-loop

图15 CCM时输出电压和电感电流仿真波形Fig.15 Simulation waveforms of output voltage and inductor current in CCM

图16 DCM1时输出电压和电感电流仿真波形Fig.16 Simulation waveforms of output voltage and inductor current in DCM1

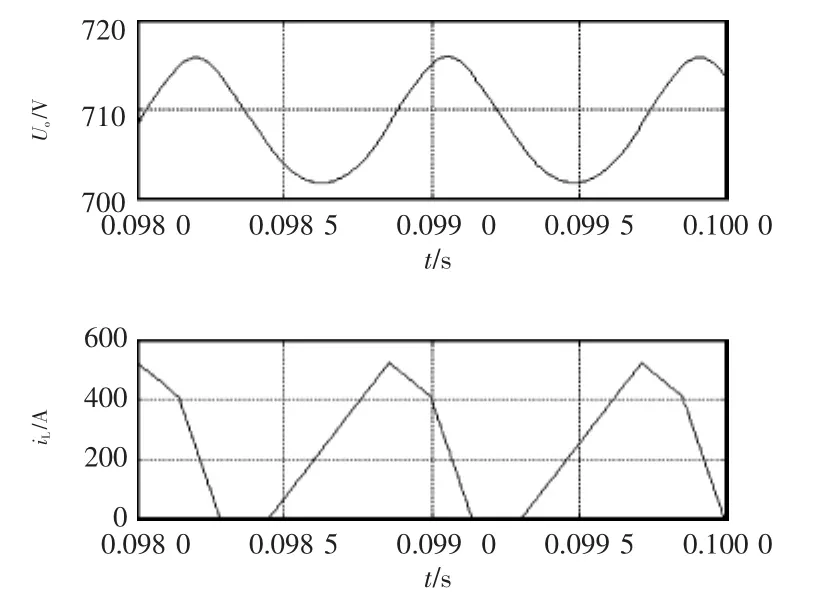
图17 DCM2时输出电压和电感电流仿真波形Fig.17 Simulation waveforms of output voltage and inductor current in DCM2

图18 DCM3时输出电压和电感电流仿真波形Fig.18 Simulation waveforms of output voltage and inductor current in DCM3

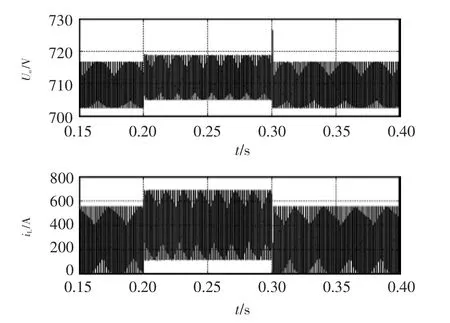
图19 DCM1与CCM切换时输出电压和电感电流仿真波形Fig.19 Simulation waveforms of output voltage and inductor current during the transition between DCM1 and CCM

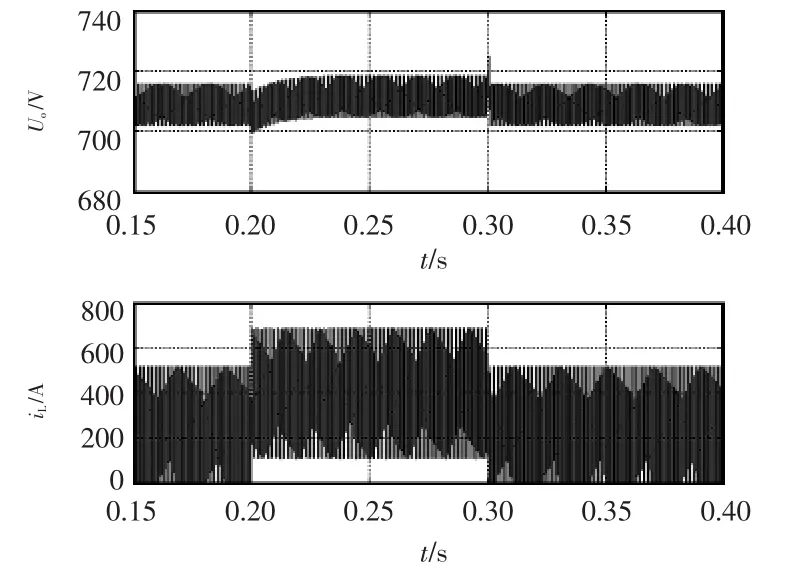
图20 DCM2与CCM切换时输出电压和电感电流仿真波形Fig.20 Simulation waveforms of output voltage and inductor current during the transition between DCM2 and CCM

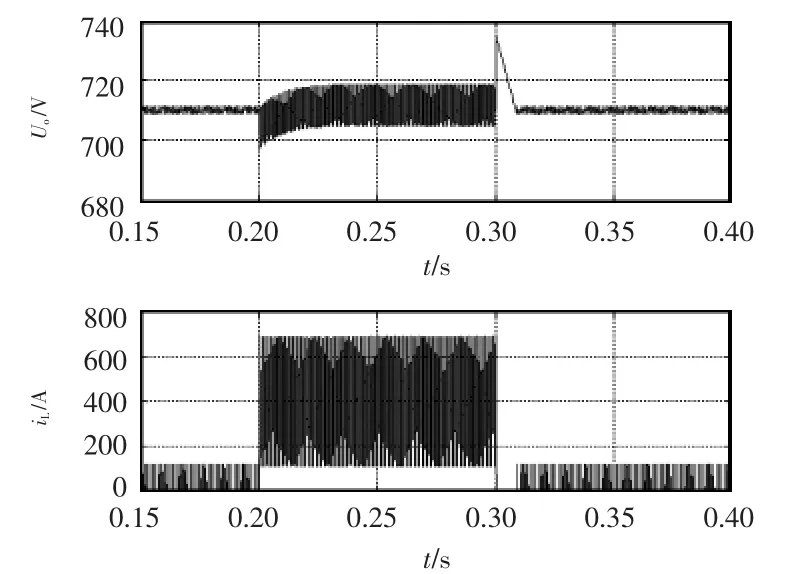
图21 DCM3与CCM切换时输出电压和电感电流仿真波形Fig.21 Simulation waveforms of output voltage and inductor current during the transition between DCM3 and CCM

4 结论

本文建立了三电平直流变换器混杂自动机模型，理论推导了4种工作模式的离散状态切换条件，仿真结果验证了切换条件的正确性，系统能够进入周期循环稳定的工作中。该模型特点如下：

（1）将输出电压稳压调节问题转化为离散状态切换条件选择问题；

（2）涵盖了 CCM、DCM1、DCM2 及 DCM3 4 种工作模式，属于大信号建模方法；

（3）4种工作模式的稳态性能均良好，模式切换过程中，动态响应快且超调小；

（4）离散状态切换条件推导过程完全在时域中进行，只需根据电路理论进行计算。

[1]Middlebrook R D,Cuk S.A general unified approach to modelling switching-converter power stages[C]//1976 IEEE Power Ele-ctronics Specialists Conference.Cleveland,USA,1976:521-550.

[2]Lee Y S.A systematic and unified approach to modeling switches in switch-mode power supplies[J].IEEE Transactions on Industrial Electronics,1985,32（4）:445-448.

[3]Sun J,Mitchell D M,Greuel M F,et al.Averaged modeling of PWM converters operating in discontinuous conduction mode[J].IEEE Transactions on Power Electronics,2001,16（4）:482-492.

[4]Erickson R W,Maksimovic D.Fundamentals of power electronics[M].2nd ed.Norwell,MA:Kluwer,2001.

[5]He Y,Luo F L.Sliding-mode control for dc-dc converters with constant switching frequency[J].IEE Proceedings-Control Theory and Applications,2006,153（1）:37-45.

[6]Naim R,Weiss G,Ben-Yaakov S.H∞control applied to boost power converters[J].IEEE Transactions on Power Electronics,1997,12（4）:677-683.

[7]Leung F H F,Tam P K S,Li C K.The control of switching dc-dc converters-a general LQR problem[J].IEEE Transactions on Industrial Electronics,1991,38（1）:65-71.

[8]Gupta T,Boudreaux R R,Nelms R M,et al.Implementation of a fuzzy controller for dc-dc converters using an inexpensive 8-b microcontroller[J].IEEE Transactions on Industrial Electronics,1997,44（5）:661-669.

[9]Geyer T,Papafotiou G,Morari M.On the optimal control of switch-mode dc-dc converters[C]//IEEE Workshop on Computers in Power Electronics.Urbara,USA,2004:148-155.

[10]Senesky M,Eirea G,Koo T J.Hybrid Modelling and control of power electronics[J].Lecture Notes in Computer Science,2003,2623:450-465.

[11]吕京航.双向直流变换器混杂系统边界条件研究[D].哈尔滨:哈尔滨工业大学,2011.Lü Jinghang.Boundary selection of hybrid system for bidirectional dc-dc switching converter[D].Harbin:Harbin Institute of Technology,2011（in Chinese）.

[12]Sreekumar C,Agarwal V.Hybrid control approach for the output voltage regulation in buck type dc-dc converter[J].IET Electric Power Applications,2007,1（6）:897-906.

[13]Sreekumar C,Agarwal V.A hybrid control algorithm for voltage regulation in dc-dc boost converter[J].IEEE Transactions on Industrial Electronics,2008,55（6）:2530-2538.

[14]Ruan Xinbo,Li Bin,Chen Qianhong.Three-level converters-a new approach for high voltage and high power DC-to-DC conversion[C]//2002 IEEE 33rd Annual Power Electronics Specialists Conference.Cairns,Australia 2002:663-668.