交错并联磁耦合双向直流变换器中多相耦合电感的设计准则

杨玉岗，张书淇，苗 闯 ，王金海 ，李秀菊

（1.辽宁工程技术大学电气与控制工程学院，葫芦岛125105；2.国网葫芦岛供电公司电力调度控制中心,葫芦岛 125000）

多相磁耦合电感因其自身结构特点，很难达到多相之间的完全对称。随着相数的增加，非对称电感的不平衡性将越来越明显，其参数与对称电感参数的差异也会越来越显著。多相并列式排布的磁耦合电感因其结构特点，各相电感之间也存在着一定的对称性和非对称性，因而磁路模型的结构形式具有一定的统一性和多样性。针对该类磁耦合电感进行设计时，要兼顾其结构特点的对称性和非对称性，以此达到更高的设计精度。

本文以四相（并列式排布）非对称磁耦合电感结构为研究基础，分析非对称耦合电感的对称度、占空比以及耦合系数的变化对双向直流变换器稳态和暂态性能的影响。给出四相非对称耦合电感运行于交错并联磁耦合双向直流变换器下的设计准则，根据设计指标，限定一定占空比下耦合系数的选取范围，即在一定的参数区域内，通过本设计准则，能够同时解决减小稳态相电流纹波、提高暂态总输出电流响应速度两大设计问题。最终通过验证此类结构的电感模型，证明理论分析的有效性。

1 磁集成交错并联双向直流变换器Buck工作模态

1.1 工作模态

四相磁集成交错并联双向直流变换器的拓扑结构和Buck工作模态如图1所示。占空比0＜D≤1/4，Buck模态下的主开关管依次滞相90°导通，而副管的导通是为了在此模态下起续流作用。四相并列式非对称耦合电感模型结构如图2所示，根据其结构对称性的特点，自感L1=L4，L2=L3；互感包括M12、M13、M14、M23、M24、M34，且有对称关系M12=M34，M13=M24。

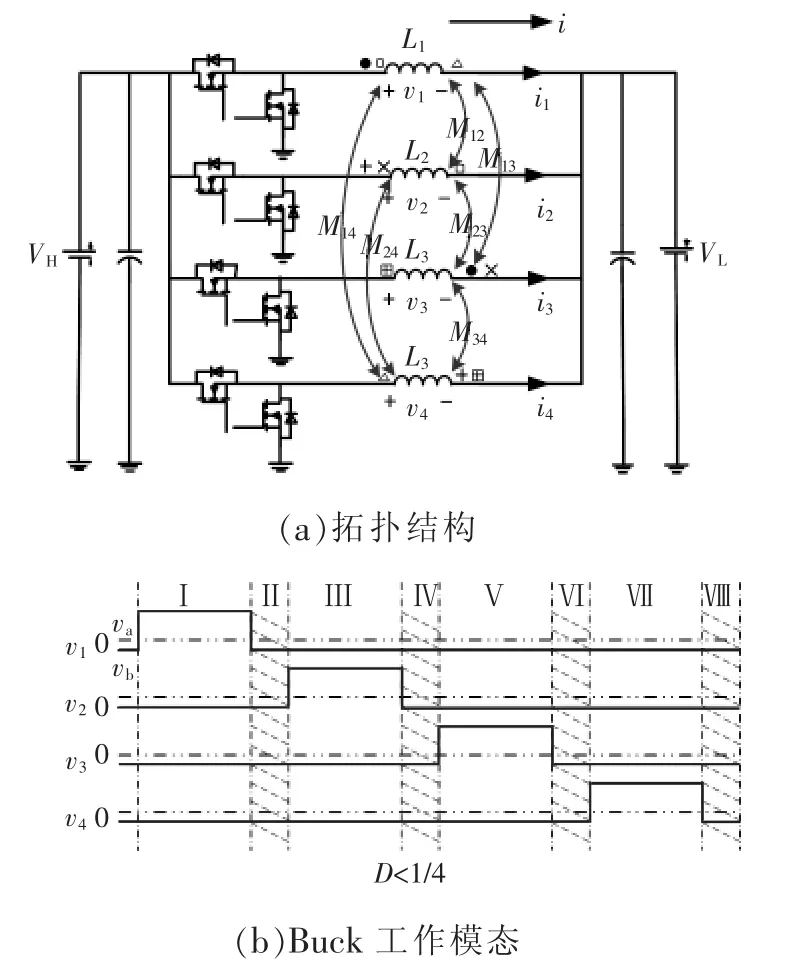
图1 四相磁集成交错并联双向直流变换器的拓扑结构及Buck工作模态Fig.1 Topology and Buck working mode of 4-phase magnetically integrated interleaving bidirectional DC-DC converter

图2 四相非对称耦合电感模型结构Fig.2 Structural model of four-phase asymmetric coupled inductors

耦合电感应用于交错并联双向直流变换器中时，各相电感两端的电压是由自身相电感与其他相互感以及各相电流共同决定的。在仅考虑两两耦合（不考虑耦合方式为正向耦合或反向耦合）的条件下，各相电感两端的电压方程[11]可以表示为

变换器高、低压侧的电压分别为VH和VL，当该通道主管导通时，由于电压钳位的作用，该相电感两端电压为va=VH-VL，而其他相电感两端电压为vb=-VL。运用解耦的方式，将各相电感两端电压表示为仅与该相电流及解耦后的等效电感有关。对照图1工作模态，分析变换器运行于各工作模态下各相电感的等效工作情况。

为简化计算结果的表达方式，用函数A1～A7进行简单等效，即

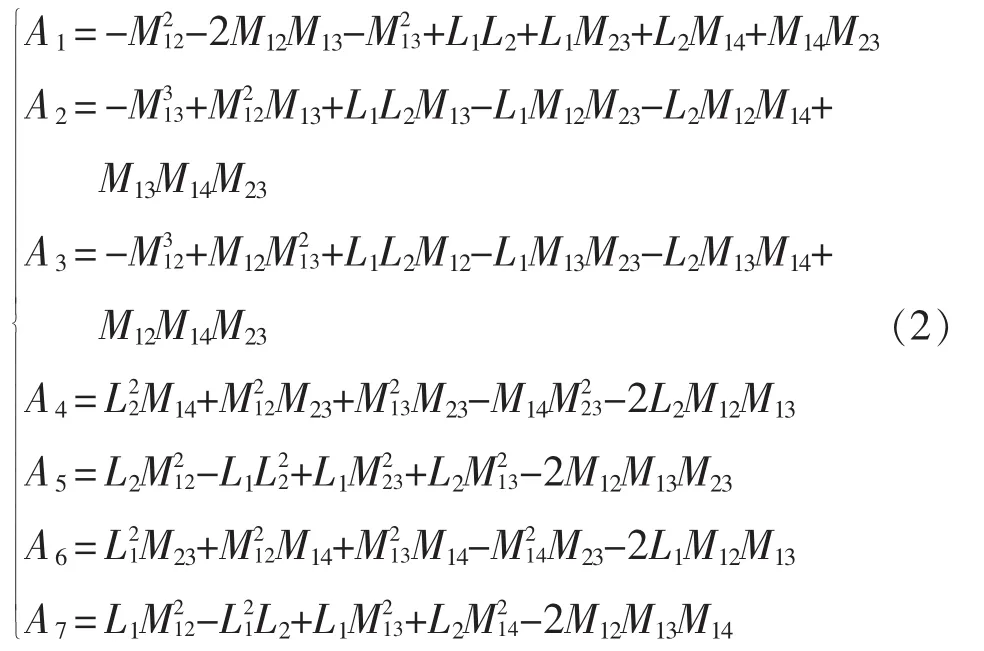
（1）工作模态 I，如图1（b）所示，v1=va，v2=v3=v4=vb，将各相电压代入式（1）可得解耦后各相的等效电感，即

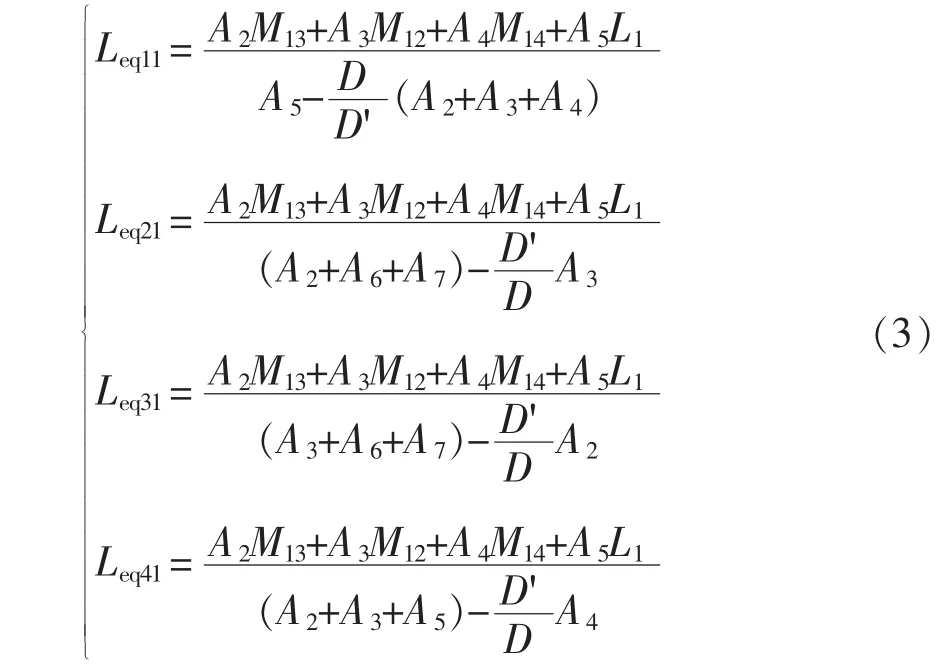
式中：D为变换器工作的占空比，D=VL/VH；D'=1-D。

同理，可得到以下等效电感。

（2）工作模态 III，v2=va，v1=v3=v4=vb，有

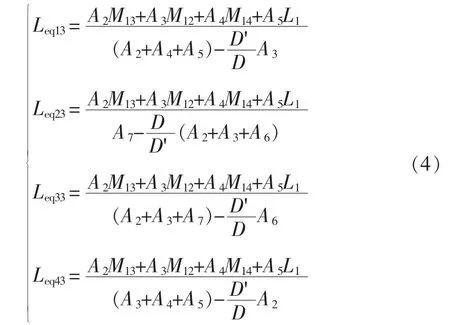
（3）工作模态 V，v3=va，v1=v2=v4=vb，有

（4）工作模态 VII，v4=va，v1=v2=v3=vb，有

（5）对于工作模态 II、IV、VI、VIII，其各相电感两端电压情况均有v1=v2=v3=v4=vb，因而得其各相解耦电感为

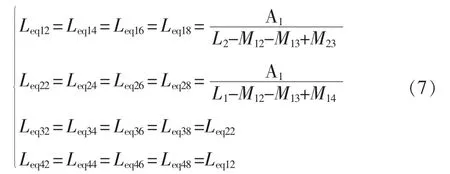
1.2 耦合电感的稳态电流和暂态电流的分析

（1）稳态分析。以耦合电感的第1相电感为例，四相非对称耦合电感的等效解耦电感Leqij（i=1；j=1,2，…,8）及各模态电流的波形如图3所示。

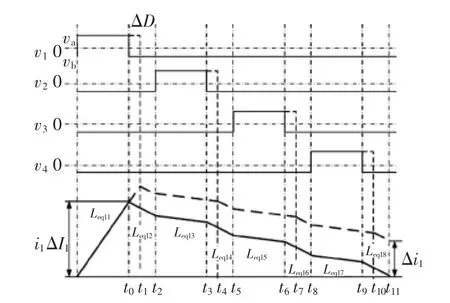
图3 四相耦合电感的稳态和暂态相电流波形Fig.3 Steady-and transient-state phase current waveforms of 4-phase coupled inductors

耦合电感的相电流波形在1个开关周期内，各通道电流的增量之和为0，因此有

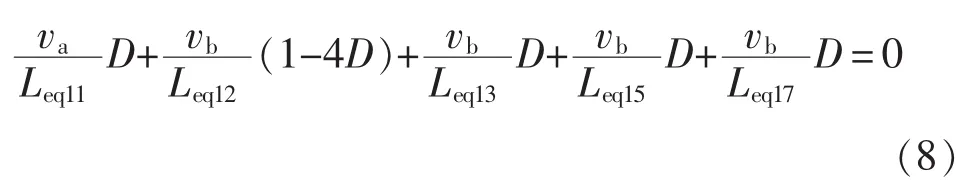
则第1相电流纹波即为第1相等效电感所引起的电流上升量，即

式中：fs为变换器的工作频率；LS1为第1通道耦合电感的等效稳态电感，可以表示为LS1=Leq11；同理其他3相绕组的等效稳态电感为：LS2=Leq23、LS3=Leq35、LS4=Leq47。

（2）暂态分析。当变换器在运行过程中负载突然发生变化时，可以通过改变工作通道的占空比来确保输出电压的变化不超过规定允许的范围[7]。若占空比增加ΔD，则四相非对称耦合电感的第1相电流变化情况（即暂态电流）如图3虚线所示，耦合电感的暂态相电流增量Δi1可表示为

把式（8）代入式（10），有

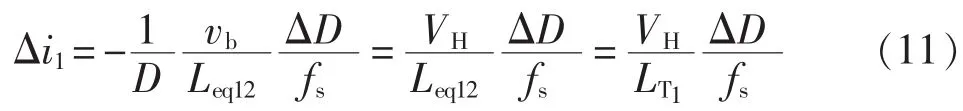
式中，LT1为第1通道耦合电感的等效暂态电感，LT1=Leq12。同理其他三相绕组的等效暂态电感为：LT2=Leq24、LT3=Leq36、LT4=Leq48。

在一个开关周期内，四相耦合电感的总输出电流增量即为各相暂态相电流增量之和，即

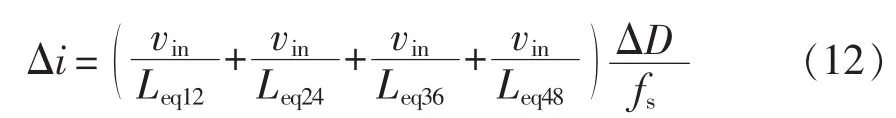
1.3 分立电感的稳态电流和暂态电流分析

（1）稳态分析。分立电感由于各通道独立，变换器工作时各相稳态电流纹波为

（2）暂态分析。当变换器占空比增加ΔD时，相电流的增量为

变换器采用分立电感的总输出电流增量即为各相暂态相电流增量之和，即

比较式（9）和式（13）、式（11）和式（14）、式（12）和式（15）可以得出，耦合电感和分立电感的稳态性能和暂态性能的差异是由于耦合电感各相解耦后的等效电感与分立电感的电感量不同所导致的。耦合电感可以通过反向耦合的耦合方式增大稳态电感或减小暂态电感。为此，对耦合情况下的稳态相电流纹波的减小量和暂态电流的增量进行定量化分析。

2 稳态电流纹波和暂态电流响应速度分析

2.1 耦合电感的稳态、暂态电感与耦合系数的关系

设k为四相非对称耦合电感的非对称度，k1、k2、k3、k4为考虑对称关系及耦合方式后的每两相之间的耦合系数（正向耦合时为正，反向耦合时为负），它们的表达式分别为

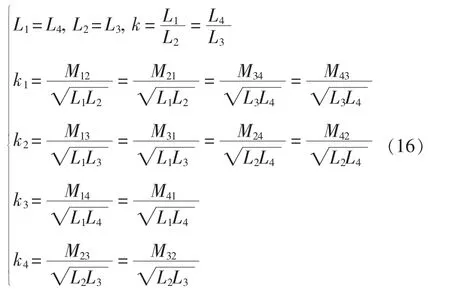
本文采取的四相耦合电感绕向相同，起始端并联接在电源侧，结束端并联接在负载侧，4个电感两两之间形成了反向耦合的关系。根据该条件，有-1/3≤ki≤0（i=1,2,3,4），0＜k＜1。将式（16）代入式（3）～式（7），得

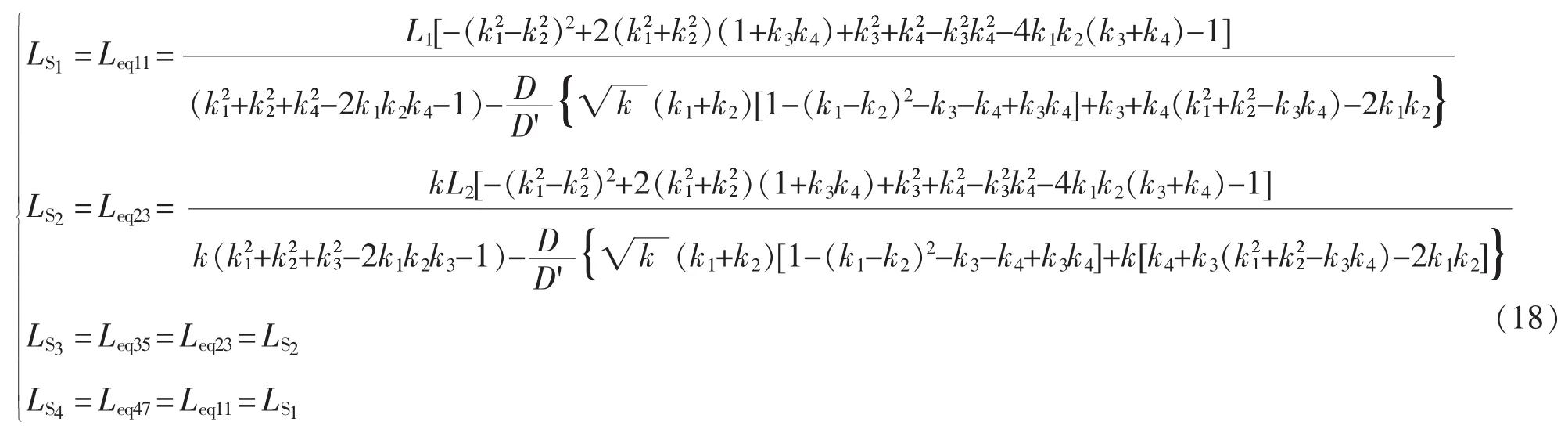
2.2 耦合电感对稳态相电流纹波和暂态响应速度的影响

根据式（9）和式（13）以及本文所研究的耦合电感的结构特点，可以得到耦合电感与分立电感的稳态相电流纹波之比，即

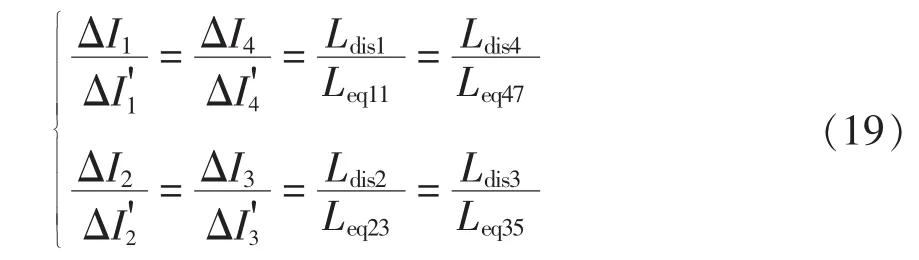
固定二者的暂态电流增量，即令变换器在采用耦合电感与分立电感时有相同的暂态相电流和总输出电流的响应速度，由式（17）和式（18）可得

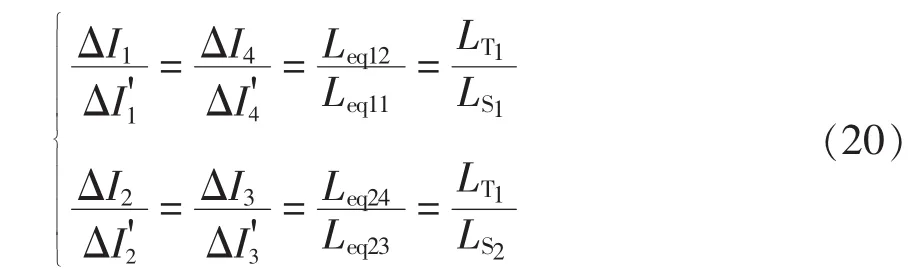
图4所示为式（20）表示的，对称度k=0.95的曲线。从曲线变化趋势来看，恒有＜1，即耦合电感的稳态相电流纹波小于分立电感；且反向耦合越强（k1、k2、k3、k4越大且数值越接近），占空比越大，相电流纹波减小得也越多。

仅改变耦合电感的对称度k=0.3时式 （20）的曲线如图5所示。比较图4和图5曲线的变化趋势，发现对称度的变化导致了非对称耦合电感相电流纹波变化的不平衡。k越小，第1、4相耦合电感的相电流纹波的减小量越小，但第2、3相耦合电感的相电流纹波减小量变大；k越近1时，四相通道的纹波减小量越接近。对于变换器而言，各通道的对称性越好，其性能越稳定；对称性越差，性能越不好，导致输出的结果越差。

耦合电感与分立电感的暂态相电流响应速度之比为

图4 k=0.95时非对称耦合电感与分立电感的稳态相电流纹波之比Fig.4 Ratio of steady-state phase current ripple of asymmetric coupled inductor to that of uncoupled inductor when k=0.95

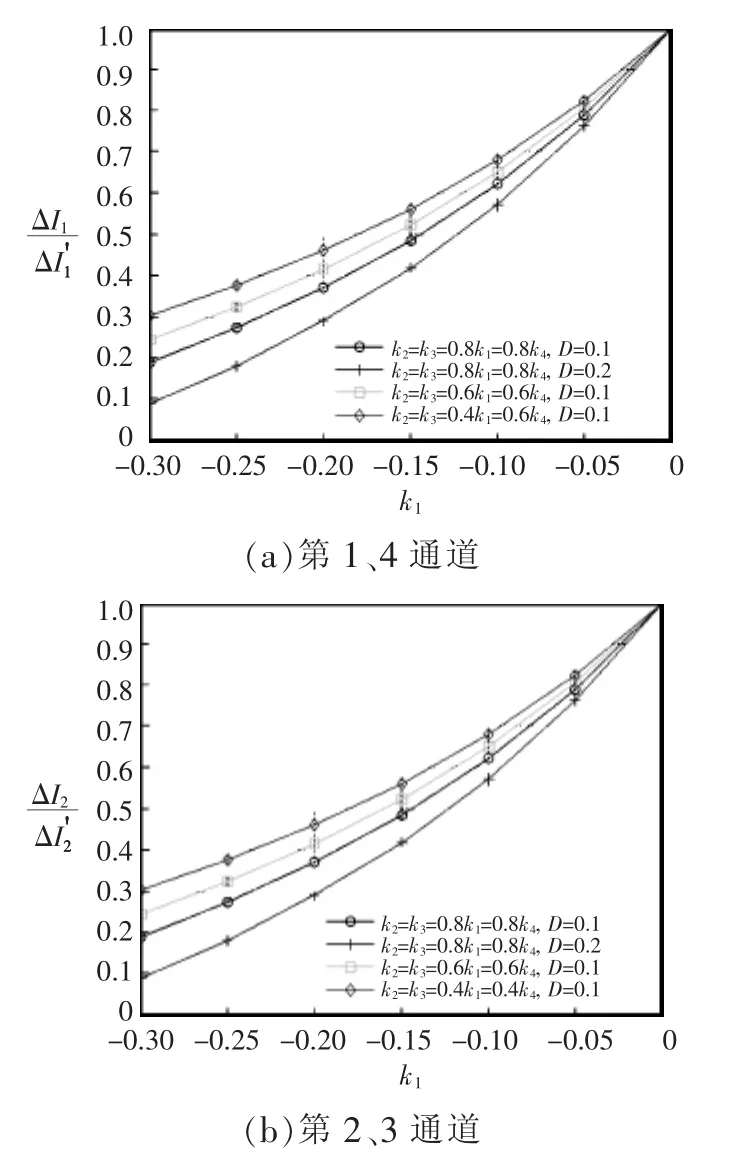
图5 k=0.3时非对称耦合电感与分立电感的稳态相电流纹波之比Fig.5 Ratio of steady-state phase current ripple of asymmetric coupled inductor to that of uncoupled inductor when k=0.3

对比四相非对称耦合电感与分立电感的暂态相电流增量与耦合系数的关系，固定二者的稳态相电流增量，由式（17）、式（18）及式（21）可得

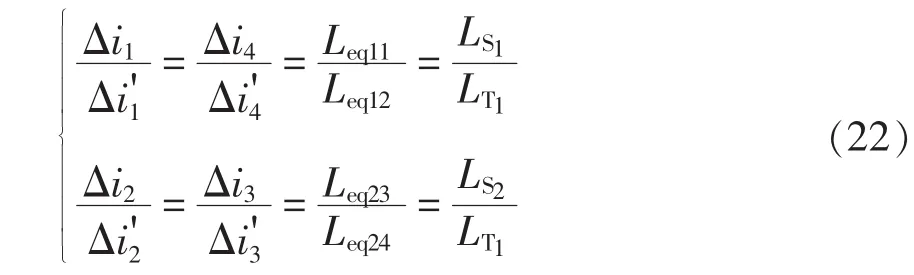
可以看出，式（22）和式（20）互为倒数关系，也就是说在对称度k=0.95的前提下，恒有，即四相非对称耦合电感的暂态电流增量均大于分立电感的暂态电流增量，且反向耦合越强（k1、k2、k3、k4越大且数值越接近）， 占空比越大，电流的增量也越大。

根据式（12）和式（15）可得，在一个开关周期内，变换器在采用四相非对称耦合电感与分立电感时，暂态总电流增量的比值为

根据式（23）绘制曲线如图6所示，在保持稳态相电流纹波相同的情况下，耦合电感的暂态总输出电流增量均大于分立电感，而且反向耦合越强，对称度越高（k 越接近于 1，k1、k2、k3、k4越大且数值越接近），占空比越大，增量越大，性能越稳定。

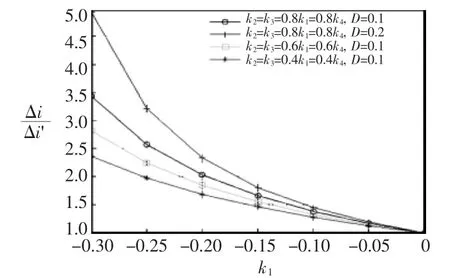
图6 非对称耦合电感与分立电感的暂态总输出电流响应速度之比Fig.6 Ratio of the total transient-state output current response speed of asymmetric coupled inductor to that of uncoupled inductor

2.3 四相交错并联磁耦合双向直流变换器中非对称耦合电感器的设计准则

以上分析的两种情况都是就改进变换器某一性能而言的，然而，在实际设计时，希望能够兼顾变换器运行过程中的稳态性能和暂态性能，这就需要在设计时兼顾耦合电感的对称度、耦合系数和占空比等一系列的相关参数。

由式（19）、式（21）、式（22）限定耦合电感同时满足减小稳态相电流纹波和增大暂态电流增量的条件为

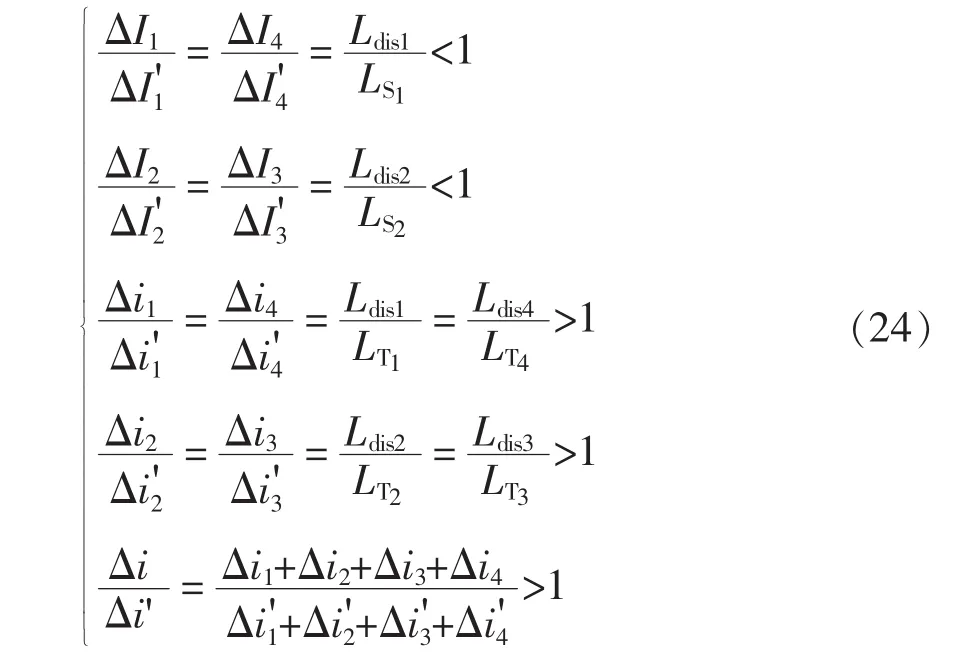
由式（23）和式（24）整理可得

Δi/Δi'、ΔI1/ΔI1'和 ΔI2/ΔI2'的三维关系如图7所示，即三者之间的取值相互制约。四相非对称耦合电感的稳态性能及暂态性能不能同时做到无限提高，当确定其中2个参数后，另一个参数也被相应确定。因此，可以通过图7粗略地选择出预期能够达到的合理化设计效果。

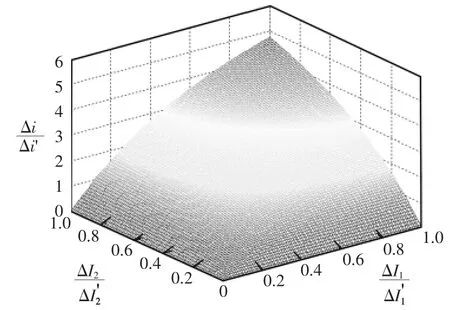
图7 Δi/Δi'、ΔI1/ΔI1'和 ΔI2/ΔI2'之间的关系Fig.7 Relationship among Δi/Δi',ΔI1/ΔI'1and ΔI2/ΔI2'

当设计四相非对称交错并联直流变换器时，根据所给出的设计指标，如通道电流纹波和暂态电流增量的要求，以及变换器的工作频率、输入输出电压、占空比等，利用式（17）、式（18）、式（24）和式（25）以及图7，合理选择四相非对称耦合电感的对称度 k 以及反向耦合系数 k1、k2、k3、k4，从而使得变换器工作于所要求的设计指标下，这就是四相非对称耦合电感应用于四相交错并联双向直流变换器的设计准则。

3 设计准则的验证

实验平台以FPGAEP4CE10E22C8为主控芯片，主电路以ISL78420为驱动芯片，在Buck模式下对四相非对称磁耦合电感的设计准则进行验证。实验条件设定为：VH=12 V，VL=1.5 V，工作频率f=125 kHz，占空比 D=0.125，ΔD=0.005，分立电感 Ldis=0.55 μH，需满足条件 ΔI1/ΔI1'≤0.5，ΔI2/ΔI2'≤0.5，Δi/Δi'≥1.5。

（1）取 k=0.973、k1=-0.263、k2=-0.239、k3=-0.232、k4=-0.248，代入式（20）～式（23），解得在 ΔI1/ΔI1'=0.5，ΔI2/ΔI2'=0.5 时，Δi/Δi'=1.56＞1.5，满足设计条件。

（2）由 Ldis=0.55 μH，据式（19）、式（21）得 L1=1.404 μH，L2=1.442 μH。

根据以上计算结果进行耦合度的选取，根据设计指标及四相非对称耦合电感的对称度要求，实验采用本实验室自主设计的四相“梯形”耦合电感结构。耦合电感的参数如表1所示，实验系统如图8所示。根据电感参数，计算耦合电感的等效暂态电感 LT1=LT4=0.366 μH，LT2=LT3=0.367 μH，等效稳态电感 LS1=LS4=1.135 μH，LS2=LS3=1.157 μH。

表1 四相非对称耦合电感参数Tab.1 Parameters of 4-phase asymmetric coupled inductors

根据以上条件，图9为稳态时的相电流的波形，可见变换器采用四相非对称耦合电感时的第1、4相和2、3相的稳态相电流纹波分别为ΔI1=9.18 A、ΔI2=9.07 A，分立电感的稳态相电流纹波ΔI1'=18.41 A， 计算得 ΔI1/ΔI1'=0.498＜0.5，ΔI2/ΔI2'=0.492＜0.5，满足设计要求。

图8 实验系统Fig.8 Experimental system

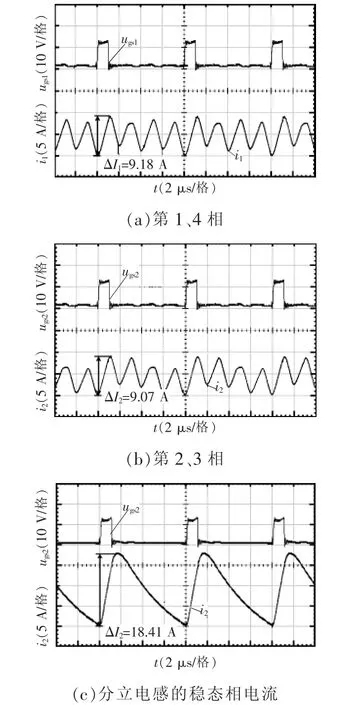
图9 耦合电感和分立电感的稳态相电流波形Fig.9 Steady-state phase current waveforms of converter with/without coupled inductors

图10为暂态时总输出电流波形。实验结果显示：耦合电感的暂态总输出电流增量Δi=6.49 A，分立电感的暂态总输出电流增量Δi'=3.84 A，计算得Δi/Δi'=1.69＞1.5，满足设计要求。由此验证了设计准则的正确性。

图10 变换器采用耦合电感器和分立电感器时的暂态总输出电流波形Fig.10 Total transient output current waveforms of converter with/without coupled inductors

4 结语

四相非对称耦合电感应用于交错并联双向直流变换器中，占空比在0～1/4的范围内，根据占空比的不同，耦合电感的对称度k以及耦合系数k1、k2、k3、k4有一个设计区域，在该设计区域内，能够同时实现变换器稳态和暂态性能的提升。耦合电感的对称度越大，耦合系数的数值越大且越接近，变换器稳定性越高。在设计四相非对称耦合电感时，根据占空比、稳态相电流纹波和暂态总输出电流响应速度的要求，利用本文给出的公式和关系合理地进行对称度和耦合系数的选择，变换器工作在理论分析设计的区域范围，满足设计要求，这就是应用于四相交错并联磁集成双向Buck-Boost变换器中非对称耦合电感的设计准则。

[1]Xie Yanhui,Sun Jing,James S.Power flow characterization of a bidirectional galvanically isolated high-power DC/DC converter over a wide operating range[J].IEEE Transactions on Power Electronics,2010,25（1）:54-66.

[2]Liang T J,Chen S M,Yang L S,et al.Ultra-large gain step-up switched-capacitor DC-DC converter with coupled inductor for alternative sources of energy[J].IEEE Transactions on Circuits and Systems,2012,59（4）:864-874.

[3]陈乾宏.开关电源中磁集成技术的应用研究[D].南京:南京航空航天大学,2001.Chen Qianhong.The application of the magnetic-integration techniques in switching power supply[D].Nanjing:Nanjing University of Aeronautics And Astronautics,2001（in Chinese）.

[4]胡海兵,王万宝,孙文进,等.LLC谐振变换器效率优化设计[J].中国电机工程学报,2013,36（18）:48-56.Hu Haibing,Wang Wanbao,Sun Wenjin,et al.Optimal efficiency design of LLC resonant converters[J].Proceedings of the CSEE,2013,33（18）:48-56（in Chinese）.

[5]杨玉岗,马杰,马云巧,等.多相交错并联双向DC/DC变换器中耦合电感的通用设计规则[J].中国电机工程学报,2015,35（23）:6122-6134.Yang Yugang,Ma Jie,Ma Yunqiao,et al.The universal design criterion of coupled inductors in multiphase interleaving and magnetically integrated bidirectional DC/DC converters[J].Proceedings of the CSEE,2015,35（23）:6122-6133（in Chinese）.

[6]杨玉岗,李涛,李海光,等.交错并联磁耦合双向 DC-DC变换器非对称耦合电感的研究[J].电工技术学报,2014,29（10）:147-156.Yang Yugang,Li Tao,Li Haiguang,et al.Research on asymmetric coupled inductor of interleaving magnetic integration bidirectional DC-DC converter[J].Transactions of China Electrotechnical Society,2014,29（10）:147-156（in Chinese）.

[7]Yang Yugang,Ma Jie,Ho N M,et al.A new coupled-inductor structure for interleaving bidirectional DC-DC converters[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2015,3（3）:841-849.

[8]李洪珠,郝文慧,杨玉岗.无气隙可改变耦合度阵列式集成磁件在交错并联变换器中的应用[J].电工技术学报,2007,22（7）:98-102.Li Hongzhu,Hao Wenhui,Yang Yugang.Application of changeable coupling degree array integrated magnetics with no air gap to staggered-shunt converter[J].Transactions of China Electrotechnical Society,2007,22（7）:98-102（in Chinese）.

[9]Liang T J,Chen S M,Yang L S,et al.Ultra-large gain step-up switched-capacitor DC-DC converter with coupled inductor for alternative sources of energy[J].IEEE Transactions on Circuits and Systems,2012,59（4）:864-874.

[10]Ho N M,Breuninger H,Pettersson S,et al.A comparative performance study of an interleaved boost converter using commercial Si and SiC diodes for PV applications[J].IEEE Transactions on Power Electronics,2013,28（1）:289-299.

[11]马杰,杨玉岗,马云巧.交错并联双向 DC/DC变换器Buck模式下的耦合电感设计规则[J].电源学报,2014,12（3）:80-86.Ma Jie,Yang Yugang,Ma Yunqiao.Coupled inductor design rule for interleaving bidirectional DC/DC converter in Buck mode[J].Journal of Power Supply,2014,12（3）:80-86（in Chinese）.