DC-DC变换器的通用大信号自适应控制策略构建

刘宿城，李晴晴，刘晓东，方 炜

（安徽工业大学电气与信息工程学院，马鞍山243032）

近年来，新能源电力的发展使得各种交直流电力电子接口的应用越来越广泛。在直流分布式电力网络中，为了便于集成光伏和储能等直流单元，DCDC开关变换器成为重要的功率接口电路，其控制要求正从以满足负载动态特性为主转向以获取最大功率为主要目标；同时一次侧能源供给和负载类型呈现出多样化和复杂性等特征，其典型表现为控制系统长期处于大信号工作状态，因此直接应用传统小信号综合方法无法确保系统在较宽工作范围内的控制性能[1-4]。

考虑到现有小信号建模与补偿的局限性，诸多学者提出了针对DC-DC开关变换器的大信号非线性控制策略，其代表性成果主要有：基于Lyapunov直接法的稳定控制[5,6]、大信号鲁棒控制[7,8]和反馈线性化控制[9,10]等。这些非线性控制方法的实现目标总体上可归结为两方面：一是借助非线性控制理论推导控制率，使DC-DC变换器非线性模型中的反馈环路尽可能线性化；二是保证系统在大信号扰动下的全局稳定性。文献[11]从系统角度推导和实验验证说明非线性控制策略能够提高DC-DC变换器系统的稳态和动态性能。然而，此类适于一般非线性系统的控制理论在用于DC-DC变换器的过程中，侧重于数学变换和处理，丢失了原有基于小信号模型的经典频域法在控制设计中所具备物理意义明确和易于补偿的优势。

为此，本文在分析DC-DC变换器的平均化大信号模型特性的基础上，以不失原有线性系统频域补偿法的优点为前提，提出一种DC-DC变换器的大信号控制策略构建思路：将系统的整体工作区间分割为若干局部子区域，针对各子区域依次设计相应的局部线性控制器，并借助权函数根据不同的工作条件实时匹配相应局部线性控制器的作用权重系数，以此达到全局自适应调节效果。首先推导了DC-DC变换器的全局化动态模型，并由此得到借助权函数凸组合构建大信号自适应控制器结构，最后分别以基本Buck变换器和Boost-Buck级联变换器为应用实例，通过仿真和实验验证了该控制策略的可行性。

1 DC-DC开关变换器的全局化模型

对于一般DC-DC变换器，平均化后的全局状态空间模型可以描述为

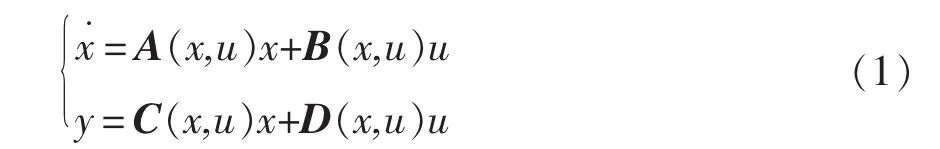
式中：x为系统状态变量；u为输入变量；y为输出变量；A、B、C、D 分别为相应的系统矩阵。

DC-DC变换器的全局模型可以通过有限个局部模型来近似描述，与非线性系统的凸多面体辨识方法是相通的。目前，已有研究将凸多面体建模思路应用于DC-DC变换器的黑箱建模中[12]，为DC-DC变换器的大信号控制设计行性提供了依据。利用该建模思想，假设将工作区域分割为n个子区域，则非线型模型（1）可以表示为

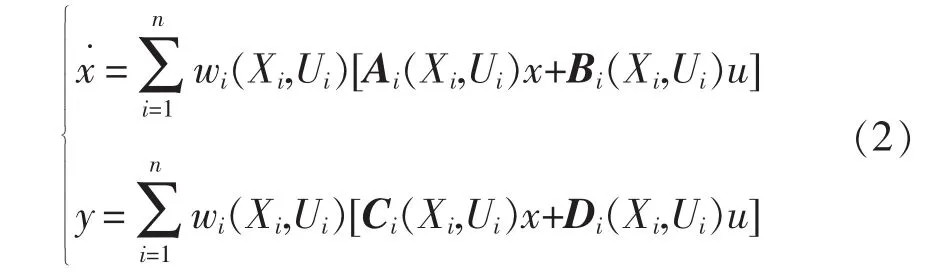
式中：Xi、Ui分别为第i个局部模型的状态变量和输入变量；wi为第i个局部模型对应的权函数，权函数可以选择高斯函数[13]、三角函数[14]和指数函数[15]等，且满足

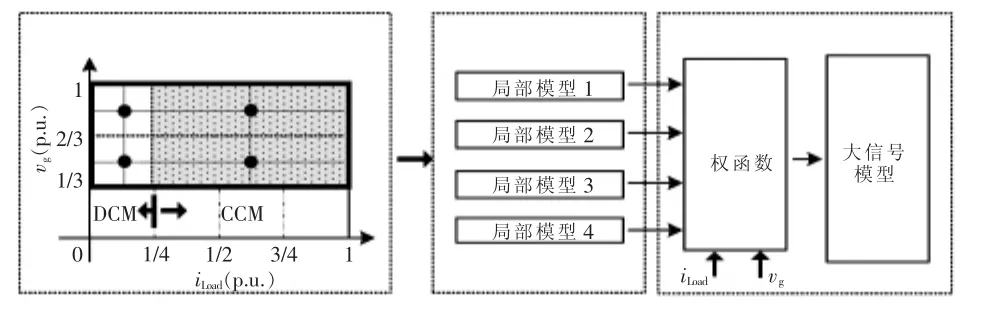
图1 DC-DC变换器的大信号建模推导过程Fig.1 Formulation the process of the large-signal modeling for DC-DC converter

图1举例说明了DC-DC变换器的全局建模推导过程，其中负载电流iLoad和输入电压vg作为工作点信息定义系统的工作区间。首先根据工作模式将DC-DC变换器全局工作区域分成4个局部工作区，然后得到每个子区域的小信号模型，再进行权函数的设计，最后通过凸组合得到DC-DC变换器的全局模型。

以具体Buck变换器为例进行说明。图2为Buck变换器的主电路原理，假设电路参数为：输入电压范围Vg=16～60 V，输出电压VO=12 V，电感L=300 μH， 电容 C=100 μF， 负载电流范围 iLoad=0～4 A，rL=0.12 Ω,rC=0.06 Ω，开关频率为 60 kHz。根据变换器的工作特性，将其工作区域分割为3个子区域，如图3所示。以每个子区域的中心作为基准工作点，分别为（16 V，2 A）、（32 V，2 A）和（48 V，2 A）。基于状态空间平均法，连续导电模式CCM（continuous conduction mode）和断续导电模式DCM（discontinuous conduction mode）Buck变换器的局部小信号模型分别为

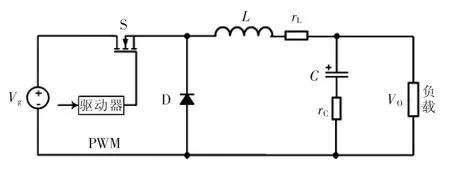
图2 Buck变换器的主电路Fig.2 Main circuit of Buck converter converter

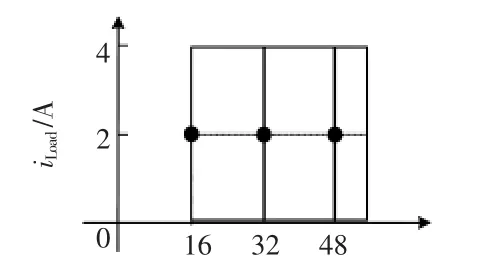
图3 Buck变换器的区域分割Fig.3 Partitioning of operation space for Buck converter

同时，从复杂度和精确性的折中考虑，将权函数选择为

当分别考虑输入电压和负载电流变化时，权函数设计为

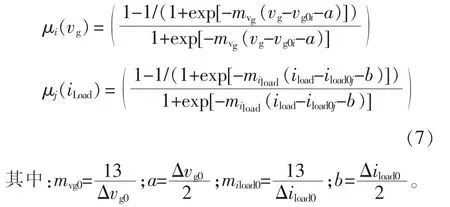
因此，Buck变换器的全局模型可近似表示为

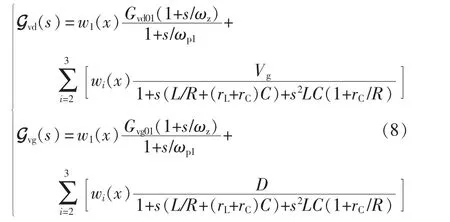
为了验证采用区域分割法建模的正确性，对Buck变换器进行了仿真验证，仿真结果如图4所示，图4（a）中包含输入电压在20 ms时刻从43 V跃变至22 V和负载电流在40 ms时刻从2.4 A跃变至1.2 A下的响应波形。从图中可以看出大信号模型基本跟踪了实际开关变换器电路的暂态响应，图4（b）为两者之间的误差，可以看出大信号模型仅在暂态响应的初期存在微小误差。由此可以看出：基于区域分割法的大信号建模能基本拟合实际开关变换器电路的大信号瞬态行为。

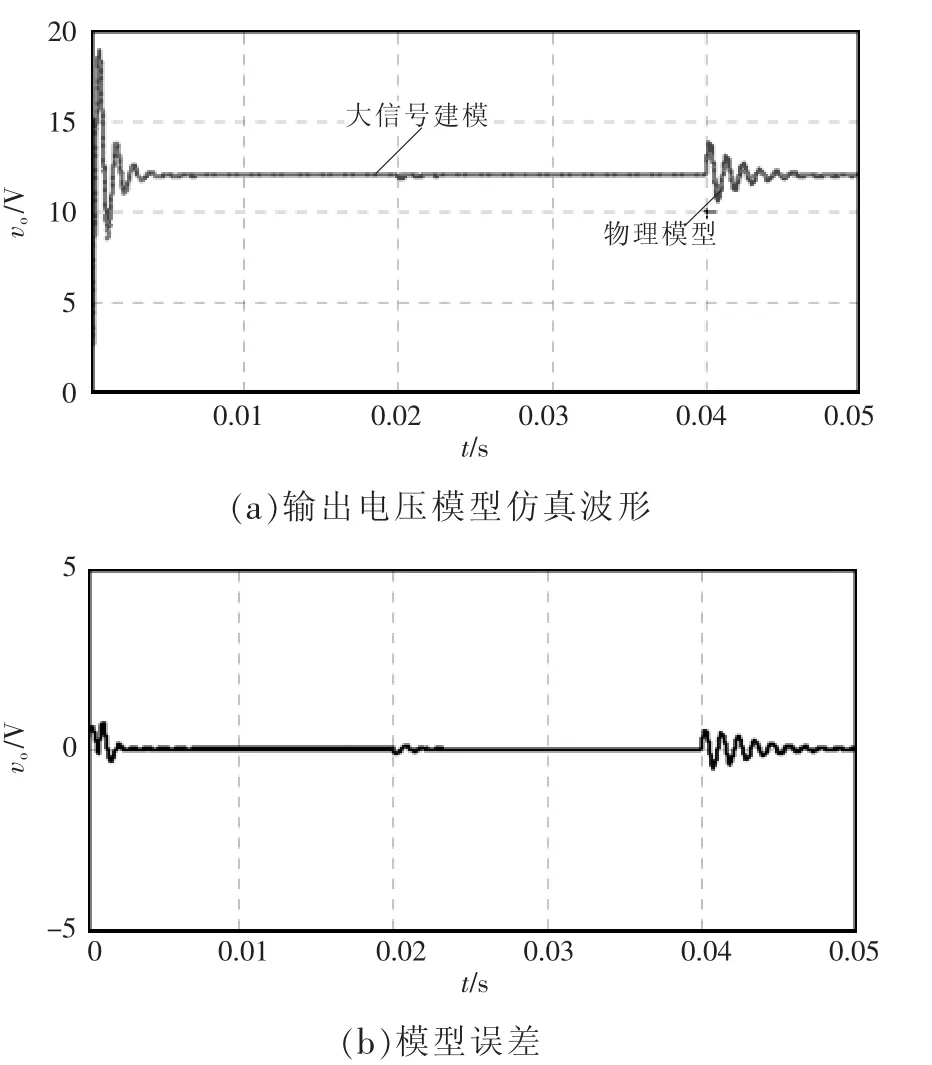
图4 大信号模型与实际电路的瞬态响应比较Fig.4 Comparison of transient responses between largesignal model and actual circuit

2 大信号自适应控制策略构建

前述分析结果表明，DC-DC变换器的全局大信号模型可通过有限局部模型近似模型，其理论依据在于每一个局部模型均存在自身的有效工作区域。以此类推，可以构建DC-DC变换器系统的通用大信号自适应控制策略，如图5所示，其中局部控制器从工程实用角度而言可选为线性控制器。控制器结构既适用于电流模式控制，也适用于电压模式控制，大信号控制策略主要应用于电压环路的自适应调节。同时，局部控制器的设计依赖于变换器相应工作子区域的局部线性模型；而权函数的输入通常为输入电压Vg和负载电流iload，由图中可知：输出到控制信号的传递函数为

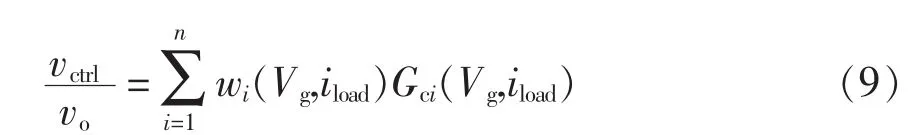
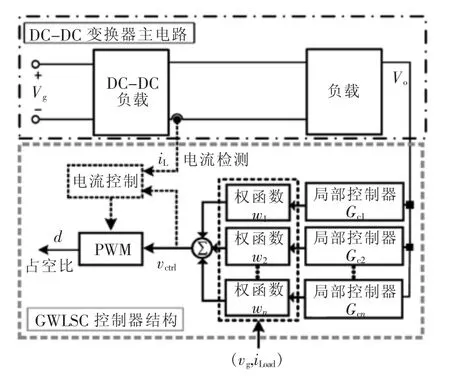
图5 DC-DC变换器的通用大信号控制器结构Fig.5 Structure of the general large-signal controller for DC-DC converter

根据式（9），DC-DC变换器系统的控制器工作机理可描述为：当变换器的工作条件（Vg和iload）处于大范围变化时，权函数实时监测工作条件的变化，并以此自适应调节各局部控制器的作用权重系数，以此确保系统在全局工作区域内的控制性能，始终保证系统具备良好的稳定性和瞬态响应。为了叙述简便，通过加权函数构建通用大信号控制GWLSC（general weighted large-signal control）策略控制。

3 设计实例

为了验证GWLSC控制策略的有效性，分别以基本Buck变换器和级联DC-DC变换器为例进行仿真和实验验证。Buck变换器的电路原理如图2所示。依据大信号建模中对Buck变换器的工作区间仍然按照图3划分为3个子区间，并选定相应的3个工作点并选择局部控制器的结构采用采用Ⅲ型超前-滞后补偿网络，其传递函数为

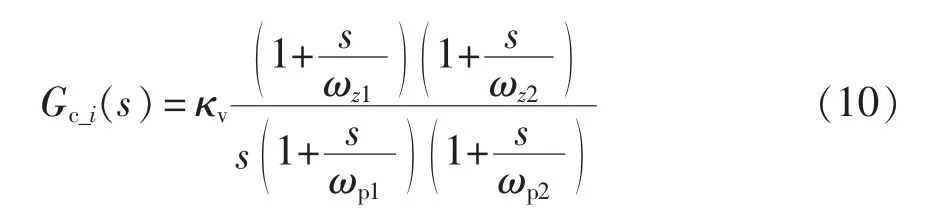
表1列出了GWLSC中3个局部控制器的参数。为了与传统线性控制效果做比较，将Gc_2选为传统线性控制器。另外，权函数采用如式（6）中指数函数形式。按照表1所示的控制参数设计，搭建了Buck变换器实验电路并进行测试。

图6和图7分别为传统线性控制和GWLSC控制的瞬态响应实验测试结果（输出电压采用交流耦合通道）。由图可以看出：对于输入电压跳变的瞬态响应，采用GWLSC控制可使输出电压超调量由1.5 V降至0.7 V，响应时间由13 ms减至5 ms；同时，对于负载电流跳变的瞬态响应，采用GWLSC控制可使输出电压超调量由1 V降至0.6 V，响应时间则 由625 μs 减 至375 μs。因此，Buck变换器在GWLSC控制下的动态性能相较于传统线性控制有较大改善。

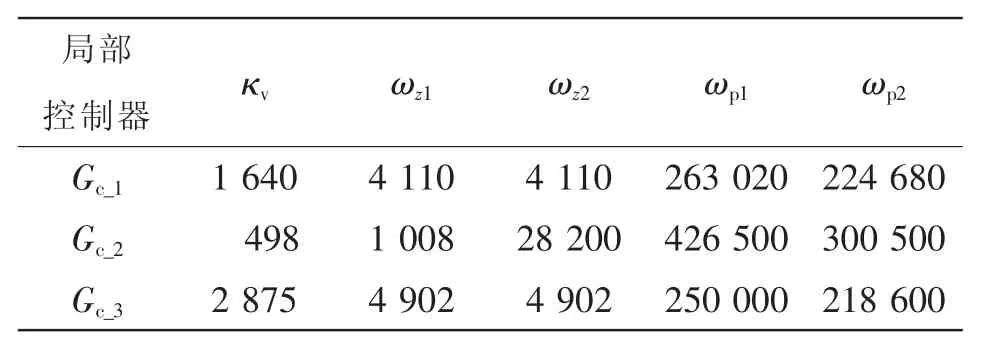
表1 Buck变换器的控制器参数Tab.1 Parameters of controllers in Buck converter

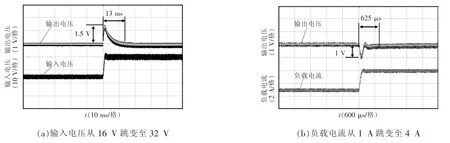
图6 传统线性控制的瞬态响应实验测试Fig.6 Testing of transient response with conventional linear control

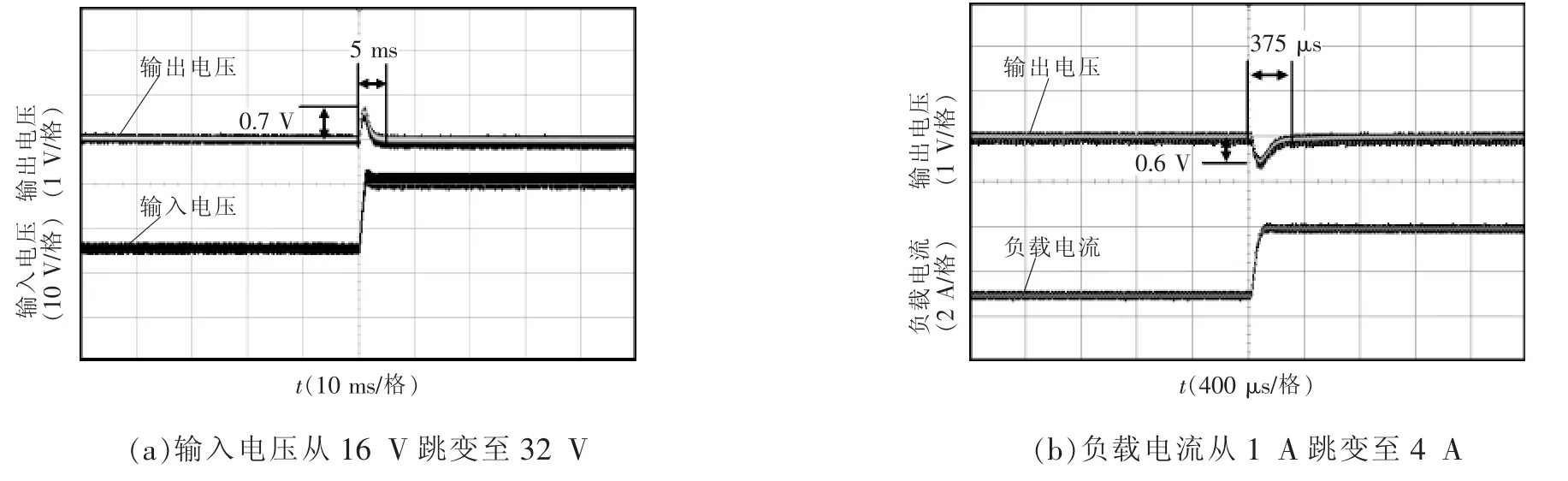
图7 GWLSC控制的瞬态响应实验测试Fig.7 Testing of transient response with GWLSC control

再以Boost和Buck变换器级联系统为例，其电路原理如图8所示。其中，源变换器采用GWLSC控制结构，负载变换器采用电压模式III型补偿器结构且参数已经确定，表2列出了级联变换器系统的局部控制器的参数。假设变换器的工作条件为：Vg=16～60 V，VO=12 V，R=4～60 Ω，开关频率设计为80 kHz。按照表2所示的控制参数设计，搭建了级联DC-DC变换器的电路仿真模型。整体仿真实验需验证两个方面的内容：控制策略的动态性能以及不同权函数对控制系统的影响。因此，仿真实验包含3种控制方式比较，即：传统线性控制、基于指数型权函数的GWLSC控制以及基于三角型权函数的GWLSC控制。

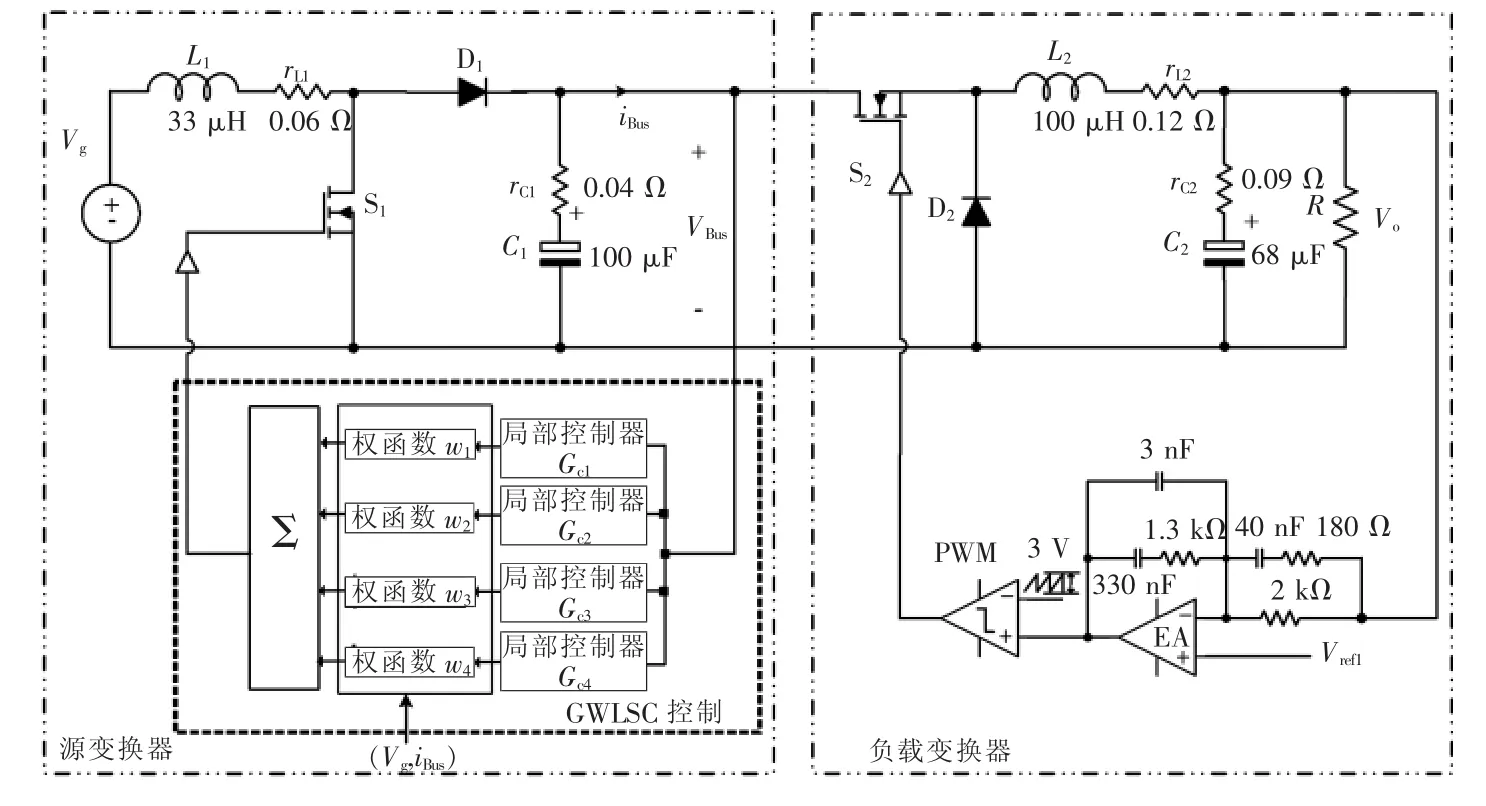
图8 级联DC-DC变换器系统的电路原理Fig.8 Schematic of circuit in cascaded DC-DC converter system

图9为负载电流跃变条件下3种控制方式的仿真实验动态响应波形，其中负载电流测试条件均为：在55 ms时负载电流发生0.8 A到2.8 A阶跃，控制输出目标为级联DC-DC变换器的母线电压VBus，其超调量和调整时间均在图中作了标注。对图9中3种控制效果的比较发现：2种GWLSC控制器均比传统线性控制器具备更优越的瞬态响应特性，二者瞬态响应的超调量和调整时间均有明显改善。进一步比较发现：基于三角型权函数的GWLSC控制相对于基于指数型权函数的GWLSC控制，前者母线电压的超调量和调整时间均略有改进；其原因在于此处设计的三角权函数在各分段处的斜率绝对值要大于指数权函数的瞬时斜率绝对值，使得对应负载电流和输入电压时，三角权函数比指数权函数选择具备较高带宽的局部控制器所占的权重较大，因此具备更优的动态性能。

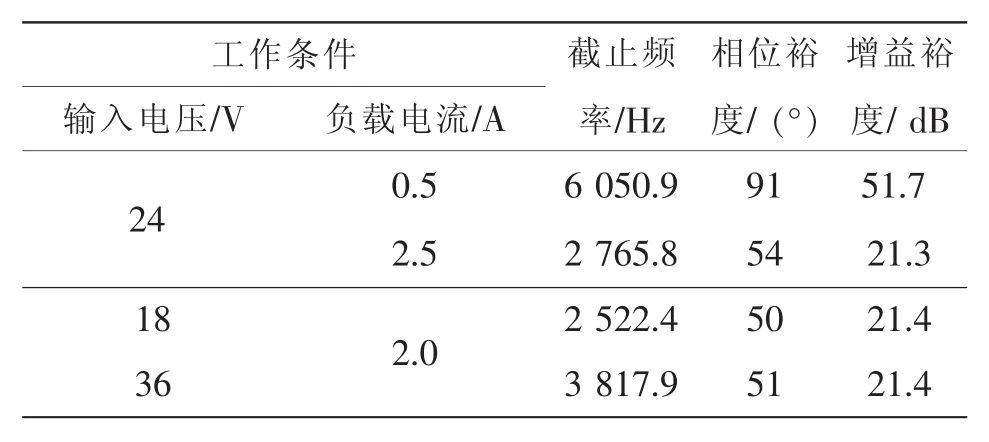
表2 GWLSC局部控制器的参数设计Tab.2 Design of parameters for GWLSC local controllers

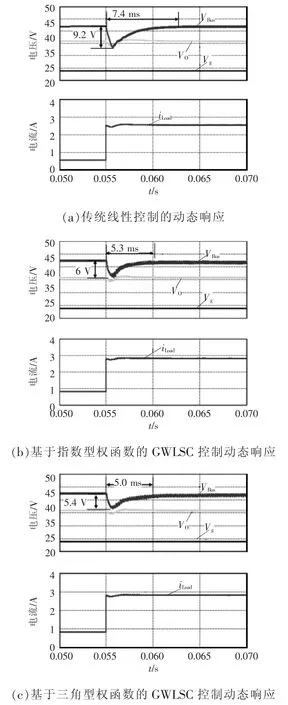
图9 3种控制方式下级联变换器的瞬态响应对比Fig.9 Comparison of transient responses of cascaded converter among three control methods

4 结语

基于传统小信号线性控制的局限性考虑，本文从线性系统频域补偿的原始思想与优点出发，提出了具备工作区域自适应功能的DC-DC变换器GWLSC大信号控制策略，并以2个实例通过实验与仿真结果验证了所提控制策略的有效性。整体而言，GWLSC控制器的设计中除了权函数的设计，其局部控制器的设计仍沿用了线性系统补偿方法，并未涉及复杂数学处理，为面向工程应用的大信号控制设计提供了可行思路。由于采用了区域分割的设计思路，因此GWLSC控制策略的构建思路具有良好通用性，也适用于包含CCM及DCM模式的宽范围工作开关变换器系统。

[1]Erickson R W,Cuk S,Middlebrook R D.Large-signal modeling and analysis of switching regulators[C].Proc.Annual Power Electronics Specialists Conference,Cambridge,USA,1982:240-250.

[2]Burgos R,Sun Jian.Guest Editorial:Special issue on modeling and control of power electronics for renewable energy and power systems[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2014,2（4）:713-714.

[3]Sanchez S,Molinas M.Large signal stability analysis at the common coupling point of a dc microgrid:a grid impedance estimation approach based on a recursive method[J].IEEE Transactions on Energy Conversion,2015,30 （1）:122-131.

[4]Liu Sucheng,Zhou Luowei,Lu Weiguo.Simple analytical approach to predict large-signal stability region of a closedloop boost DC-DC converter[J].IET Power Electronics,2013,6（3）:488-494.

[5]Sanders S R,Verghese G C.Lyapunov-based control for switched power converters[J].IEEE Transactions on Power Electronics,1992,7（1）:17-24.

[6]Hu Tingshu.A nonlinear-system approach to analysis and design of power-electronic converters with saturation and bilinear terms[J].IEEE Transactions on Power Electronics,2011,26（2）:399-410.

[7]吴爱国,李际涛,黄瑞祥,等.DC-DC变换器的大信号建模及鲁棒控制方法[J].电子学报,2001,29（5）:649-652.Wu Aiguo,Li Jitao,Huang Ruixiang,et al.Large signal modeling and robust control for DC-DC converters[J].Acta Electronica Sinica,2001,29（5）:649-652（in Chinese）.

[8]Olalla C,Queinnec I,Leyva R,et al.Optimal state-feedback control of bilinear dc-dc converters with guaranteed regions of stability[J].IEEE Transactions on Industrial Electronics,2012,59（10）:3868-3880.

[9]刘锦波,明文龙.一种基于输入/输出反馈线性化的Boost型DC/DC变换器非线性控制方案[J].中国电机工程学报,2010,30（27）:55-61.Liu Jinbo,Ming Wenlong.A novel scheme of nonlinear control strategy based on input-output linearization for boost type dc/dc converter[J].Proceedings of the CSEE,2010,30（27）:55-61（in Chinese）.

[10]Bacha S,Munteanu I,Bratcu A I.Feedback-linearization control applied to power electronic converters,in power electronic converters modeling and control[M].Germany:Springer,2014:307-336.

[11]Sira-Ramirez H.Are nonlinear controllers really necessary in power electronics devices[C]Proc.Annual European Conference on Power Electronics and Applications,Dresden,Germany,2005:1-10.

[12]Arnedo L,Burgos R,Boroyevich D,et al.System-level black-box DC-to-DC converter models[C].Proc.Annual IEEE Applied Power Electronics Conference and Exposition,Washington,USA,2009:1476-1481.

[13]Gregorcic G,Lightbody G.Local model network identification with Gaussian processes[J].IEEE Transactions on Neural Networks,2007,18（5）:1404-1423.

[14]Takagi T,Sugeno M.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Tansactions on Systems Man and Cybernetics,1985,15（1）:116-132.

[15]Cao S C,Rees N W,Feng G.Quadratic stability analysis and design of continuous-time fuzzy control systems[J].International Journal of Systems Science,1996,27（2）:193-203.