高频Boost变换器稳定运行的参数域分析

李 山 ，崔 森 ，陈 艳 ，司文旭 ，张俊凯

（1.重庆理工大学电气与电子工程学院，重庆400054；2.重庆市能源互联网工程技术研究中心，重庆400054；3.西安通信学院装备技术保障教研室，西安 710106）

在电力电子变换器中，一方面由于非线性元件的存在，另一方面电力电子变换器中的功率器件均工作在开关状态，而不是线性放大状态，因此周期性的开通和关断功率变换器容易导致非线性行为的产生。目前，随着对电力电子系统中分岔行为识别的研究已经比较成熟，DC/DC功率变换器的非线性行为研究已经成为有关学术界和工程界关注的热点之一[1-3]。

Boost变换器是非线性现象研究的一个重要对象，目前对其非线性行为的研究主要集中在典型低频率变换器非线性行为的分析与控制上。在实际的DC/DC变换器设计中，尤其是本文所研究的高频变换器，其稳定运行参数域的确定一直是科研与工程设计人员所十分关心的问题。通常是通过调整变换器中的某些参数来使系统性能得到改善，与此同时也会致使系统中其他方面的性能无法实现，主要原因在于设计人员没有清楚地掌握不同参数对系统稳定性的影响，因此，研究确定系统参数稳定域对功率变换器系统稳定性及其变换器的设计和运行都有着重要的现实意义。

本文利用非线性动力学的研究方法[4]分析了各个参数之间对高频Boost变换器稳定性的影响，根据DC/DC功率变换器的频闪映射[5]模型与Jacobian矩阵[6]来判断稳定域的范围，通过电路仿真及实验确定了影响变换器稳定运行主要参数的稳定域分布，进而对高频Boost变换器的稳定性分析和设计提供了重要的参考价值。

1 高频Boost变换器的工作原理及建模

1.1 高频Boost变换器的工作原理

本文主要研究峰值电流模式控制[7-8]的高频Boost变换器，根据开关管的工作状态，可得到以下两种工作模式，该电路在这两种工作模式下周期性的切换，如图1所示。

当开关S导通、D截止时，即图1（a）所示的情况，可得电路的微分方程

式中：iL为高频Boost变换器的电感电流；uc为电容电压；R为负载电阻；uin为输入电压。

当S关断、D导通时，即图1（b）所示的情况，可得电路的微分方程

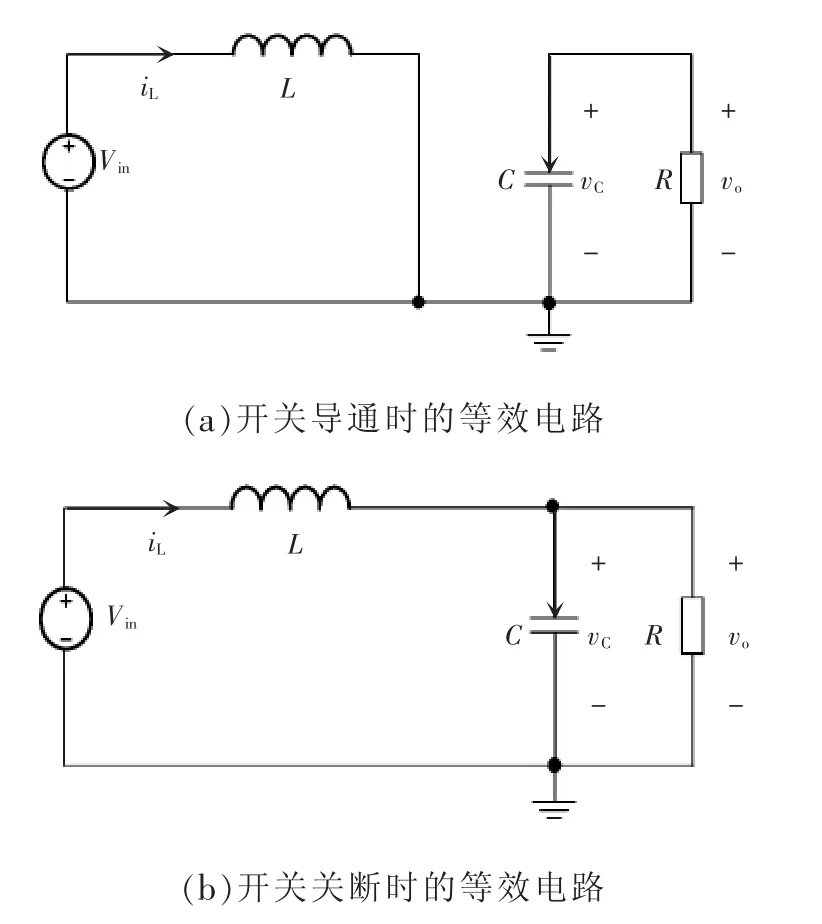
图1 高频Boost变换器工作时的两种拓扑结构Fig.1 Two topologies of high-frequency Boost converter in working mode

高频Boost变换器的开关导通与关断由时钟信号clock周期性的控制，clock信号每隔一段固定的时间就会使RS触发器重新置位，即Q=1，使开关导通；开关导通后电感电流上升，当达到电流给定值Iref后，比较器输出信号翻转，将R-S触发器复位，即Q=0，并使开关关断。峰值电流模式控制系统稳定性好，响应速度快，实现也很容易，并且能够限制电路的峰值电流，从而保护器件。该模式是目前使用最为广泛的电流模式控制方式。

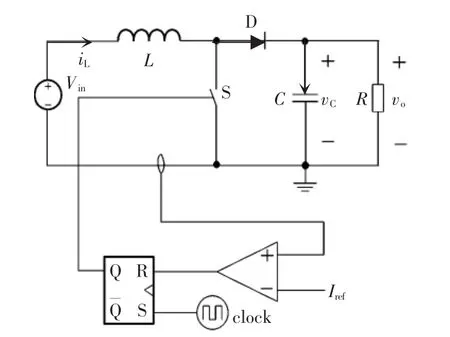
图2 峰值电流模式控制的原理Fig.2 Principle of peak current mode control

1.2 高频Boost变换器的精确离散迭代映射模型

从DC/DC功率变换器微分方程可得到该系统为分段光滑非线性动力学系统，直接通过上述方程来分析系统性能存在很大困难，本文利用已广泛应用于研究功率变换器非线性现象的离散迭代映射方程来分析其稳定性。由式（1）和式（2）可得电路的状态方程为

在频闪映射下的离散模型为

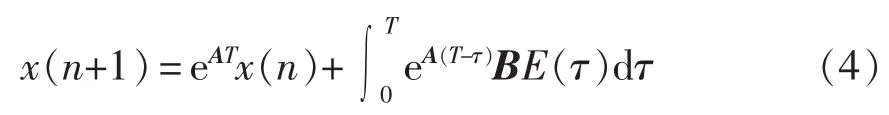
现系统的状态方程为式（3）和式（4），可以得到系统在第n个周期的离散模型如下。

（1）当 nT＜t＜nT+dnT 时，有

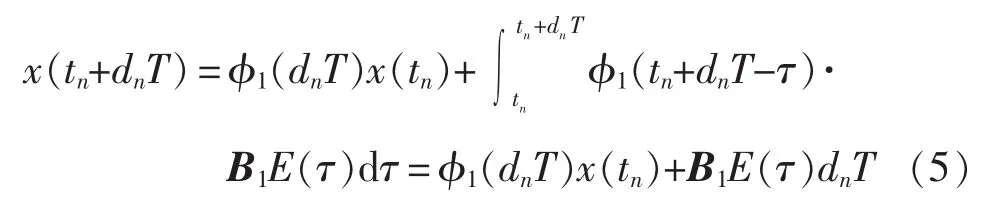
（2）当 nT+dnT＜t＜（n+1）T 时，有

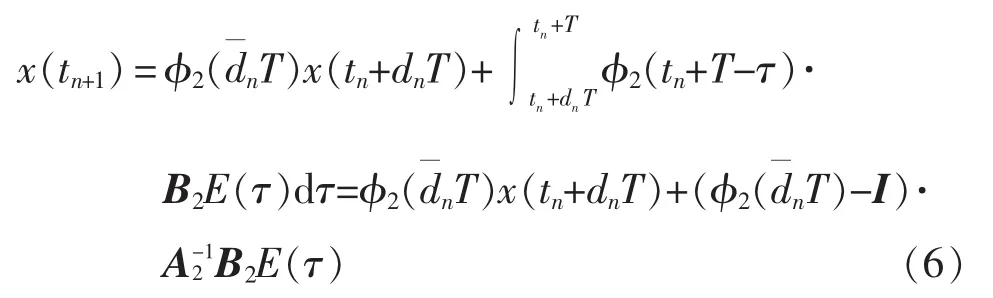
其中：；I 为单位矩阵；E 为系统输入电压；A1、A2、B1和 B2均为系统状态参数矩阵。

将式（5）代入式（6）并整理得离散映射方程为

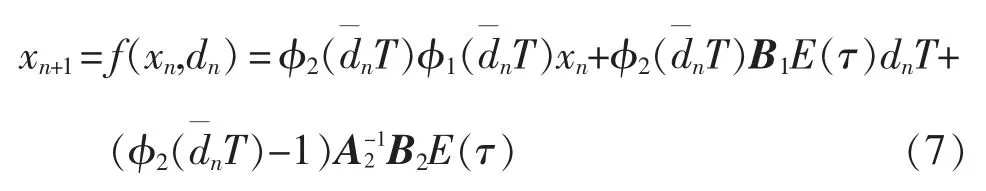
定义切换函数为

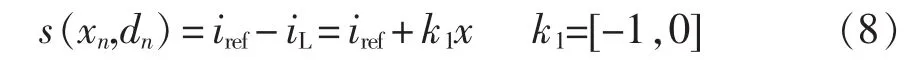
则当s（xn,dn）=0时开关S的状态出现变换，状态由 Q=1 变化为 Q=0，联立式（7）和式（8），就构成 Boost变换器的离散映射方程。

2 高频Boost变换器稳定性分析

Jacobian矩阵是分析稳定性的有效工具，本文利用Jacobian矩阵来分析变换器不动点的稳定性，从而确定高频Boost变换器的稳定域，首先建立不动点的Jacobian矩阵。假设被控系统稳定在单周期态，且认为输入电压和参考电压始终保持不变，取，XQ和D为稳态单周期解。对xn+1=f（xn,dn）进行小信号线性化扰动处理[9-10]，有

由 s（xn,dn）=0，并化简得

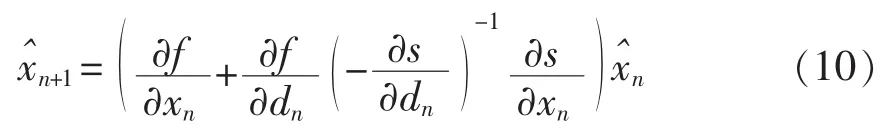
则对应的Jacobian矩阵为

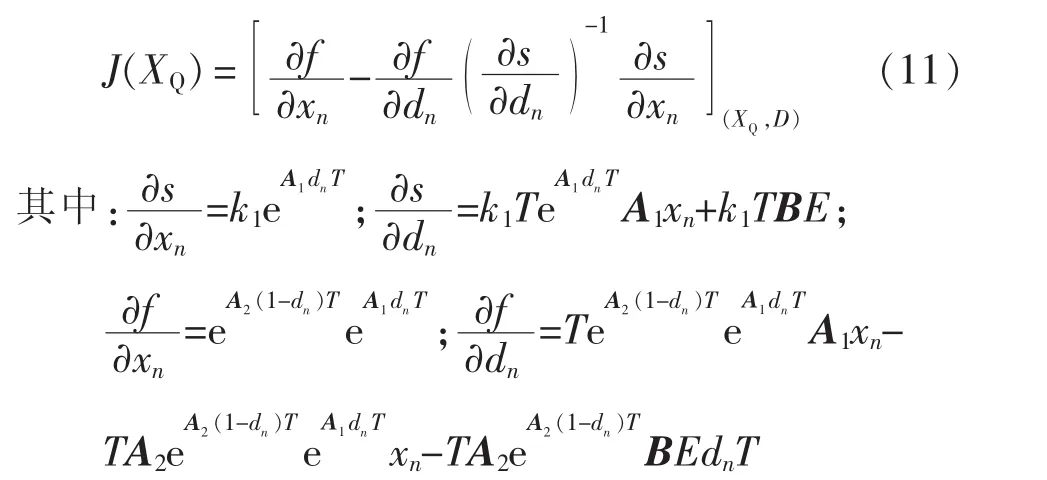
不妨记λ为J的特征值，由系统稳定性知，当λ均落在单位圆内，即|λ|＜1时，则系统稳定。在计算系统Jacobian矩阵特征值之前，首先要确定出被控Boost变换器系统离散映射方程的稳态周期解XQ和D，其求解单周期稳态解的过程如下。

设 xn+1=xn=XQ，x（nT+dnT）=XD，dn=D,由式（5）和式（6）得

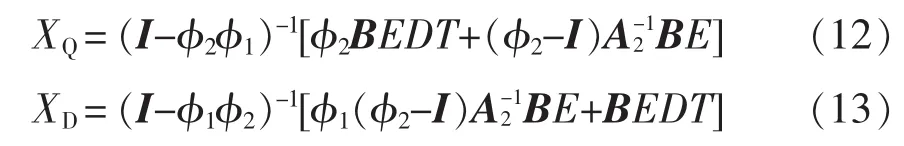
同时，切换函数满足条件为

联立式（12）至式（14），利用数值运算即可求得稳态周期解XQ和D。然后通过稳态时的周期解来求Jacobian矩阵的特征值，从而判断系统的稳定性。

根据图2所示的峰值电流模式控制高频Boost变换器的原理，按下列参数计算Jacobian矩阵的特征值：uin=10 V，L=1 mH，R=22 Ω，C=12 μf，f=100 kHz，Iref=0.5～5.5 A。

例如当Iref=1.0 A时，利用数值运算求得稳态周期解分别为

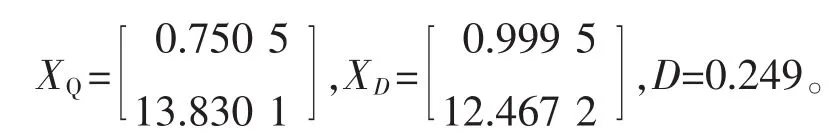
此时的Jacobian矩阵为

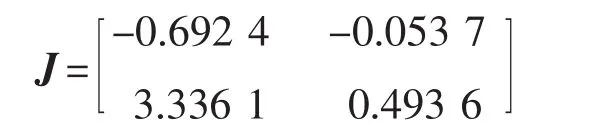
其特征值为：λ1=-0.514 8，λ2=0.316 0。由于|λ1|＜1且|λ2|＜1，故 Iref=1.0 A 时系统是稳定的，此时系统的确处于单周期稳态。当Iref=1.0～5.5 A时，Jacobian矩阵最大模特征值的变化如图3所示。其中，|λmax|=max{|λ1|，|λ2|}。由图3 可以看出，当 Iref取 1.7～1.8 A之间的某个值时，|λmax|会超过1，从而导致系统进入不稳定状态。

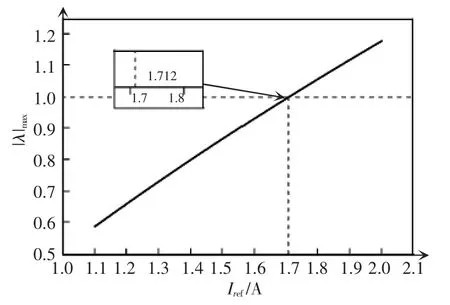
图3 Jacobian矩阵最大模特征值的变化轨迹Fig.3 Changing trajectory of the maximum modulus eigenvalue of Jacobian matrix

为求出这个Iref的临界值，考虑当Iref=1～2 A时Jacobian矩阵特征值的变化，结果如表1所示。由表1 可看出，当 Iref≈1.7 A 时，|λ|接近 1，通过大量的数值计算，可以算出当Iref=1.712 A时，λ1=1.000 2，λ2=1.373 8，即此时的Iref为使系统不稳定的临界值，超过此值系统就会进入不稳定状态。当电流Iref小于1.712 A时，系统在不动点处雅可比矩阵的特征值均小于1，此时不动点是稳定的节点；当Iref超过1.712 A时，λ从实轴的负半轴穿过单位圆，系统发生倍周期分岔，此时系统原有的周期1不动点失去稳定，取而代之的出现2个稳定的周期2解。对于本文所研究的高频Boost变换器其Jacobian矩阵特征值均在坐标轴的实轴上变化，并且|λ1|的变化比|λ2|迅速，由于只要有一个特征值超过单位圆系统就变得不稳定，因此这里选取了最大模特征值|λ1|作为研究系统稳定性的依据。

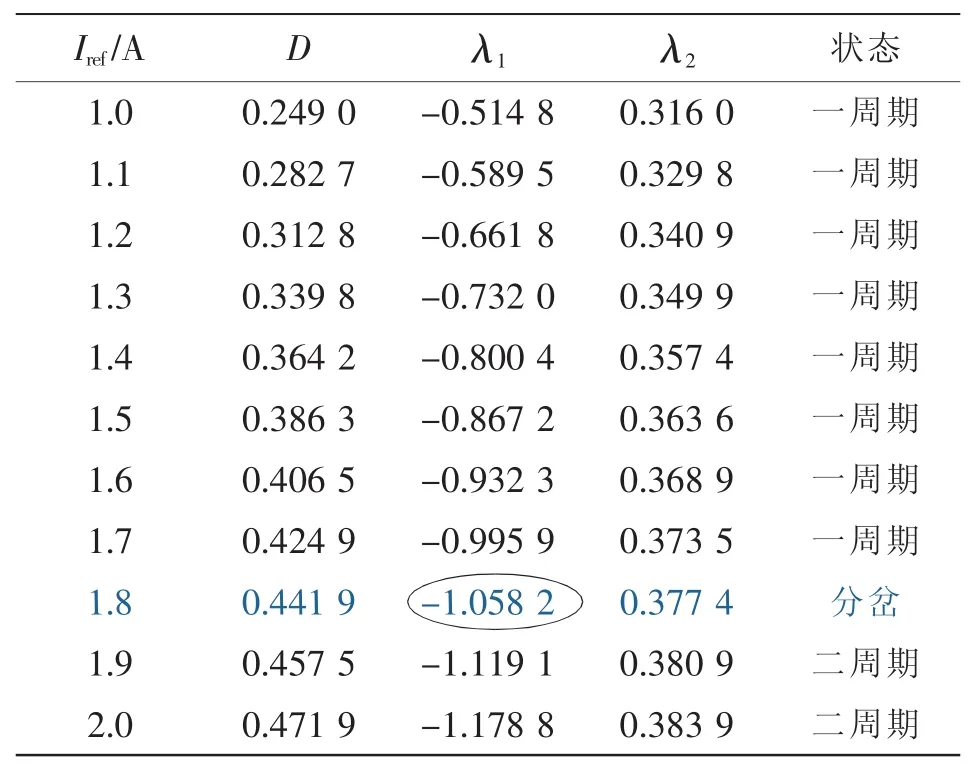
表1 变换器的Jacobian矩阵特征值Tab.1 Eigenvalues of converter's Jacobian matrix

3 高频Boost变换器稳定运行参数域分析

利用Jacobian矩阵特征值的变化可精确地判断分岔点[11]的位置，确保系统工作在稳定的区域。分别选择参考电流Iref、电路中的电感L和电容C来分析其不同参数值对高频Boost变换器系统稳定性的影响，以此来确定该系统的稳定区域。图4分别给出了上述对应的不动点稳定区域边界。由图4（a）可见，曲线上方为稳定区，随着Iref不断增加，电感L不动点的稳定区域持续增大；由图4（b）可见，随着Iref的增加，电容C不动点的稳定区域将会变小；图4（c）所示为上述3个参数所形成的稳定区域分布。

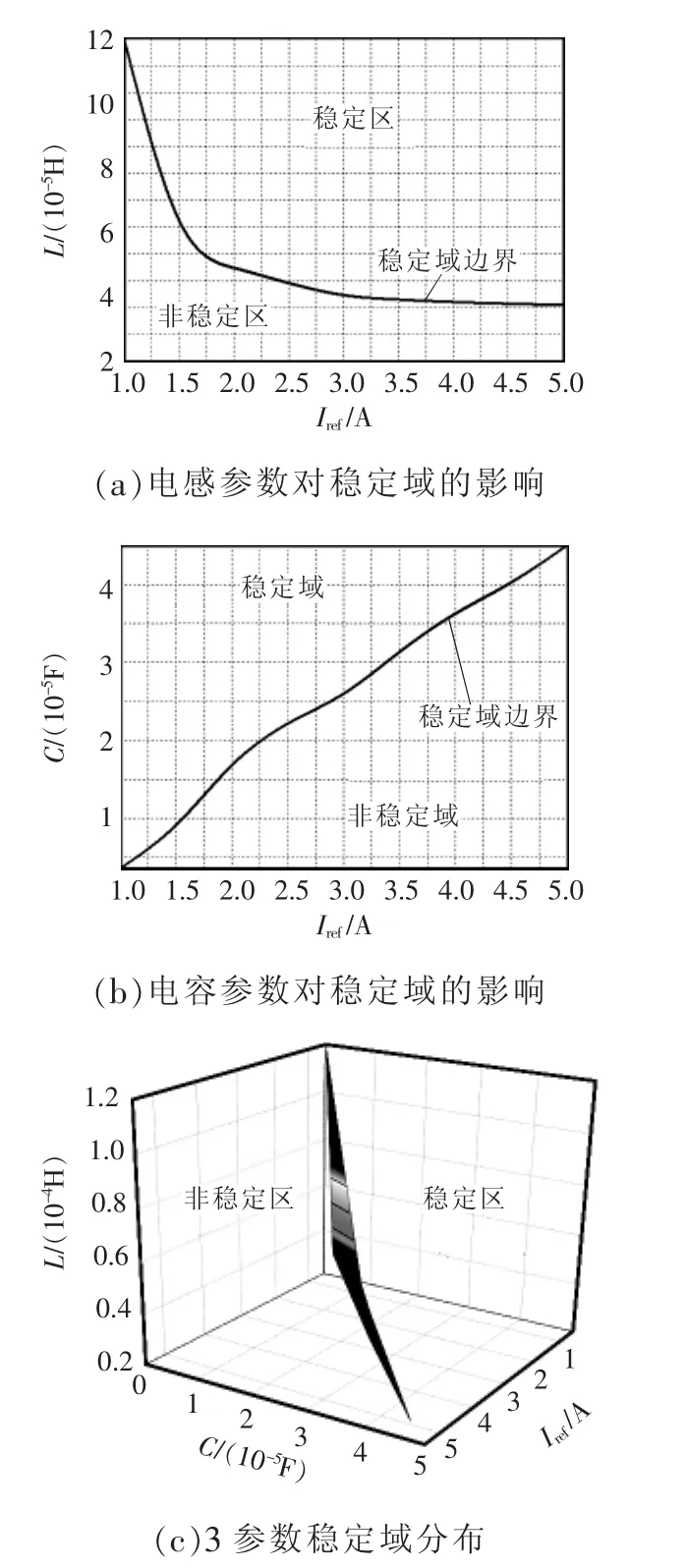
图4 不同参数变化下的稳定域边界曲线Fig.4 Boundary curves of stability region with variations of different parameters

4 数值仿真及实验分析

根据高频Boost变换器系统性能特点，以参考电流为分岔参数进行仿真。首先以参考电流为分岔参数进行仿真，电路参数如下：输入电压uin=10 V，电感 L=1 mH，电容 C=12 μF，时钟频率 f=100 kHz，负载电阻R=20 Ω。当参考电流Iref=0.5～5.5 A之间变化时，电感电流iL的分岔如图5所示。

由图5可得，在Iref≈1.712 A时，系统由周期1分岔成周期2；在Iref≈2.63 A时，再次发生倍周期分岔，在Iref≈4.97 A时，系统进入混沌状态。该图反映了在参考电流变化的过程中，系统经倍周期分岔进入混沌的整个过程。

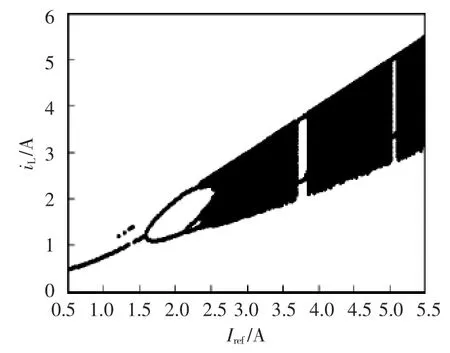
图5 以参考电流Iref为变化参数的电感电流分岔Fig.5 Bifurcation diagram of inductance current with reference current Irefas an varying parameter

通过MATLAB对电路进行仿真，分别得到了Iref=1.0 A（单周期态）、Iref=2.0 A（周期 2 状态）、Iref=4.0 A（混沌状态）的电感电流iL和电容电压uc波形，并且通过庞加莱映射图[12-13]进一步反映出在参考电流不同的情况下，系统出现的分岔混沌现象，如图6所示。

为了验证上述理论分析和变换器电路仿真的正确性，以参考电流Iref做为分岔参数为例，进行了相关的电路验证分析，按照上文所给参数搭建了基于峰值电流控模式下的高频boost变换器电路模型，实验电路图与上述仿真模型一致。给定电路参数：输入电压uin=10 V，f=100 kHz，负载电阻 R=20 Ω，电感 L=1 mH，电容 C=12 μF,电感等效电阻 r=0.02 Ω，电路中电感电流与电容电压的实验波形如图7所示。

由实验结果可知，通道1与通道2分别显示了周期1、周期2和混沌状态下的电感电流iL与电容电压uc。图7（a）所示为参考电流Iref=1 A时周期1状态下的稳定波形；图7（b）所示为Iref=2 A是周期2状态下的波形；图7（c）为Iref=4 A时系统进入混沌状态。实验波形与仿真结果基本吻合，验证了上述理论分析的正确性。

5 结语

本文在对Boost变换器现有非线性理论研究成果的基础上，对高频Boost变换器的稳定运行参数域进行了研究，通过建立该变换器的精确离散迭代映射方程，以Jacobian矩阵特征值变化做为判稳依据，结合光伏发电系统动态变化情况选择并网参考电流Iref作为分岔参数，通过实验与理论分析相结合，验证了系统的非线性特性，并在此基础上确定了高频Boost变换器电路参数的稳定运行区域。本文为Boost变换器在高频条件下系统稳定运行提供了参考，也为系统参数的优化及性能的提升提供了理论依据。

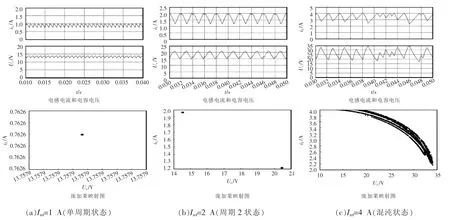
图6 不同参考电流下电感电流和电容电压仿真波形Fig.6 Simulation waveforms of inductance current and capacitance voltage under different reference currents

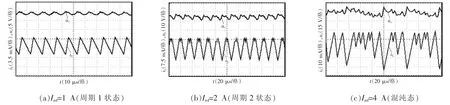
图7 不同参考电流下电感电流iL与电容电压uc实验波形Fig.7 Experimental waveforms of inductor current and capacitor voltage under different reference currents

[1]毕闯,向勇,张千,等.Buck ZCS PWM变换器非线性动力学研究[J].系统仿真学报,2014,26（3）:710-714.Bi Chuang,Xiang Yong,Zhang Qian,et al.Nonlinear dynamics of buck ZCS PWM converter[J].Journal of System Simulation,2014,26（3）:710-714（in Chinese）.

[2]雷涛,陈伉.双单元Buck变换器中非线性动力学仿真研究[J].系统仿真学报,2014,26（8）:1820-1824.Lei Tao,Chen Kang.Study of nonlinear dynamics analysis in two cell buck converters[J].Journal of System Simulation,2014,26（8）:1820-1824（in Chinese）.

[3]Tse C K,Bemardo M D.Complex behavior in switching power converters[J].Proceeding of the IEEE,2002,90（5）:768-781.

[4]李耀伟,彭战松,俞建宁.三维自治系统的稳定性分析及其分岔研究[J].重庆理工大学学报,2013,27（10）:121-124.Li Yaowei,Peng Zhansong,Yu Jianning.Three-dimensional autonomous system stability and bifurcation analysis[J].Journal of Chongqing University of Technology,2013,27（10）:121-124（in Chinese）.

[5]尚佳宁,边境,李虹,等.基于频闪映射的LCL型并网逆变器的稳定性分析[J].电工技术学报,2014,29（1）:251-256.Shang Jianing,Bian Jing,Li Hong,et al.The stability analysis of grid-connected inverter with LCL filter based on the stroboscopic map[J].Transactions of China Electrotechnical Society,2014,29（1）:251-256（in Chinese）.

[6]刘啸天,周国华,李振华,等.基于双缘调制的数字电压型控制Buck变换器离散迭代映射模型建模与动力学分析[J].物理学报,2015,64（22）:414-425.Liu Xiaotian,Zhou Guohua,Li Zhenhua,et al.Discrete iterative-map modeling and dynamical analysis of digital voltage-mode controlled buck converter with dual-edge mo dulation[J].Acta Physica Sinica,2015,64（22）:414-425（in Chinese）.

[7]周国华,许建平,包伯成,等.电流源负载峰值电流控制buck变换器的复杂次谐波振荡现象[J].物理学报,2011,60（1）:51-58.Zhou Guohua,Xu Jianping,Bao Bocheng,et al.Complex subharmonic oscillation phenomenon of peak current controlled buck converter with current source load[J].Acta Physica Sinica,2011,60（1）:51-58（in Chinese）.

[8]王均,杜建华,纪婧,等.峰值电流模式控制数字移相全桥变换器的分析与设计[J].电源学报,2015,13（2）:71-76.Wang Jun,Du Jianhua,Ji Jing,et al.Analysis and design of digital peak-current-control scheme in phase-shift fullbridge converter[J].Journal of Power Supply,2015,13（2）:71-76（in Chinese）.

[9]黄汉奇,毛承雄,陆继明,等.光伏发电系统的小信号建模与分析[J].中国电机工程学报,2012,32（22）:7-14.Huang Hanqi,Mao Chengxiong,Lu Jiming,et al.Small signal modeling and analysis of grid-connected photovoltaic generationsystems[J].ProceedingsoftheCSEE,2012,32（22）:7-14（inChinese）.

[10]邵桂荣,苏世栋,詹平红.DC-DC开关变换器的动力学建模与稳定性分析[J].重庆理工大学学报,2010,24（11）:93-96.Shao Guirong,Su Shidong,Zhan Pinghong.Dynamic modeling and stability study of DC-DC switching converters[J].Journal of Chongqing Institute of Technology,2010,24（11）:93-96（in Chinese）.

[11]Chen Yan,Zheng Yong.Nonlinear behavior analysis of Z-source DC/DC Inverter based on current control[J].IEEE Transactions on Vibroengineering,2013,15（3）:25-29.

[12]周小勇.一个新混沌系统及其电路仿真[J].物理学报,2012,61（3）:71-79.Zhou Xiaoyong.A novel chaotic system and its circuit simulation[J].Acta Physica Sinica,2012,61（3）:71-79（in Chinese）.

[13]兰朝凤,苏文涛,李小斌.水轮机压力脉动的混沌动力学特性[J].哈尔滨工业大学学报,2016,48（7）:101-105.Lan Chaofeng,Su Wentao,Li Xiaobin.Study on the chaotic dynamic characteristics of pressure fluctuations in hydro-turbine[J].Journal of Harbin Institute of Technology,2016,48（7）:101-105（in Chinese）.