新型Z源不对称三电平逆变器及中点电位控制方法研究
2018-06-01魏金成邱晓初
马 黎,魏金成,邱晓初,魏 力
(西华大学电气与电子信息学院,成都 610039)
多电平逆变器因其灵活的控制方式、较高的逆变效率和低电压谐波含量输出等优点,在高压大功率交流电动机的变频调速、有源电力滤波、风力发电和太阳能发电等领域中得到了广泛的应用[1]。但是多电平逆变器属于降压型变换器,在实际应用中若要获得更高的输出电压,就需要在直流电源和逆变器输入之间增加一级升压电路,这无疑将增加系统的硬件成本,降低系统的工作效率[2-3]。为克服这一缺点,文献[4]提出了一种单Z源中点箝位型NPC(neutral point clamped)三电平逆变器。Z源网络的引入使直通成为一种正常的工作状态[5-7],通过控制直通占空比,可以实现升压输出,此外还提高了系统的可靠性,消除了死区效应对逆变器的影响[8]。
但是单Z源NPC逆变器主电路所需的器件多,控制及驱动电路都较为复杂[9]。故本文提出了一种新型Z源不对称三电平逆变电路。相较于单Z源NPC逆变电路,在没有增加功率开关管数量的情况下,不需要箝位二极管,不仅减小了系统体积还节约了硬件成本,同时保持了Z源三电平逆变器的固有优势。
然而三电平逆变器直流侧采用电容分压的形式,导致逆变器中点电位不平衡问题无法规避。该问题会导致系统输出的低次谐波增加,某些开关器件承受电压上升,严重时会缩短直流侧电容和开关器件的寿命[10]。因此,中点电位平衡问题一直是三电平逆变器研究的重点[11-12]。
本文根据单Z源NPC逆变器的空间矢量脉宽调制 SVPWM(space vector pulse width modulation)方法以及上、下直通状态对中点电位的影响,提出一种适用于新型Z源不对称三电平逆变器的最优SVPWM控制策略,阐述了上、下直通矢量的插入策略,最大程度地减小了直通作用产生的开关损耗,有效抑制了中点电位的直流偏移。通过仿真结果验证了理论分析的可行性和正确性。
1 新型Z源不对称三电平逆变器的拓扑结构及工作原理
1.1 拓扑结构
不对称三电平逆变器与NPC三电平逆变器的拓扑结构如图1所示。与NPC三电平逆变器相比,不对称三电平逆变器不需要箝位二极管,并且没有增加功率开关管的数量,有助于减小逆变器的空间,节约硬件成本。Udc表示电源电压,从开关管耐压值来看,NPC三电平逆变器4个开关管Sa1~Sa4耐压值均为0.5Udc;不对称三电平逆变器的开关管Sa4耐压值为Udc,其余3个开关管Sa1~Sa3耐压值均为0.5Udc。然而由于NPC型器件本身的差异,2个开关管不可能完全均分直流侧电压,因此开关管在设计时的耐压值也会大于0.5Udc,不能明显体现出NPC型在耐压值上的优越性。其对比结果如表1所示。
综上所述,本文选取了不对称型三电平逆变器与Z源逆变器相结合,构成了一种新型Z源不对称三电平逆变器,拓扑结构如图2所示。
图中,在逆变器的直流输入电源与逆变桥之间引入1个Z源网络,2只电感L1、L2和2只电容C1、C2构成一个 X 型,且 L1=L2,C1=C2,UL1=UL2=UL,UC1=UC2=UC;直流侧电源电压为Udc;直流侧的2只分压电容CS1、CS2相等,CS1=CS2=CS,故每只分压电容上的电压约为Udc/2;Ui为Z源网络的输出电压;分压电容的中点O与不对称三电平逆变桥臂的中点相连;二极管D1和D2是为了在直通状态时起到反向阻断的作用。

图1 三电平逆变器拓扑结构Fig.1 Topological structure of three-level inverter

表1 不对称型与NPC型三电平逆变器电路比较Tab.1 Comparison between asymmetric and NPC-type three-level inverter circuits

图2 新型Z源不对称三电平逆变器拓扑结构Fig.2 Topological structure of novel Z-source asymmetric three-level inverter
1.2 工作原理
由于Z源网络通过逆变桥臂直通实现升压,因此Z源三电平逆变器除了具有传统逆变器的有效状态和零状态外,还单独具有上、下直通状态。以A相桥臂为例,介绍了该逆变电路的5种不同状态,如图3所示。图中:P表示有效状态“1”;O表示零状态;N表示有效状态 “-1”;U表示上直通状态;L表示下直通状态。
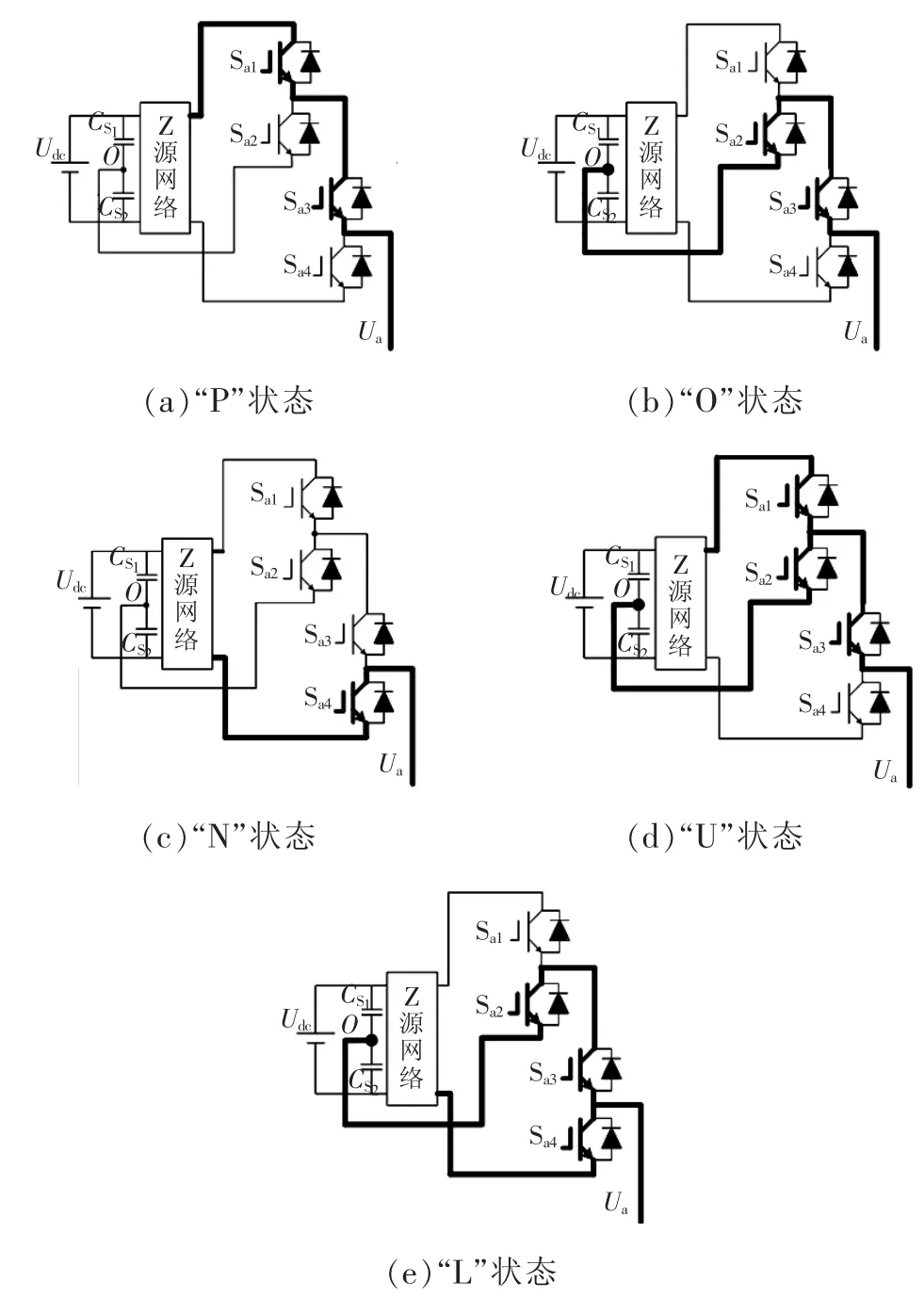
图3 新型电路拓扑A相桥臂5种状态Fig.3 Five states of the novel circuit topology for phase-A bridge-arm
表2列出了 A相桥臂的 4个开关管 Sa1、Sa2、Sa3、Sa4的开关状态以及相对应的输出电压。表中:ON表示功率开关管导通;OFF表示功率开关管关断。与传统Z源NPC逆变器相比,新型拓扑处于“N”状态时,开关管Sa1和Sa2的状态有2种组合。这样在设计控制算法时,就可以有多种选择方案,使功率开关管的通断状态和通断时间更加灵活,能够平衡功率器件的损耗,给散热器的设计带来了方便。

表2 A相桥臂开关状态及相应输出电压Tab.2 Switching states of phase-A bridge-arm and the corresponding output voltages
为使Z源网络输出电压Ui保持平衡,1个开关周期T内的上直通和下直通时间[13]需满足

式中,TU、TL和TD分别为上、下直通时间和桥臂有效直通时间。
稳态条件下,Z源网络输出电压Ui[14]为

式中,D为直通占空比,D=TD/T。因此,逆变器输出相电压峰值可表示为
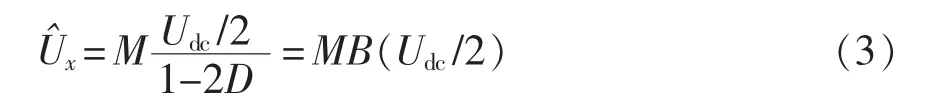
式中:M 为调制比;B 为升压比,B=1/(1-2D)。
由式(3)可知,当 B=1(即 D=0)时,新型 Z 源不对称三电平逆变器工作在传统降压模式;当B>1(即D>0)时,则工作在升压模式。
2 控制算法
2.1 传统Z源三电平SVPWM
单Z源三电平逆变器的SVPWM技术是在传统SVPWM基础上,通过合理地插入上、下直通矢量,产生的一种适合于单Z源三电平逆变器的调制方法,主要可以分为:区域判断、矢量状态次序确定、时间计算、直通矢量插入和时间状态分配5部分[15]。图4所示为其基本空间矢量图,图中,6个大矢量将整个区域分为6个正三角形区域,依次编号为 S1、S2、S3、S4、S5、S6; 每个大扇区 60°, 又可分为 6个小区,编号1~6,图5为扇区S1的小区划分,V*表示空间矢量落在了扇区S1的小区5,由基本矢量V1P(V2N)、V7、V13合成。
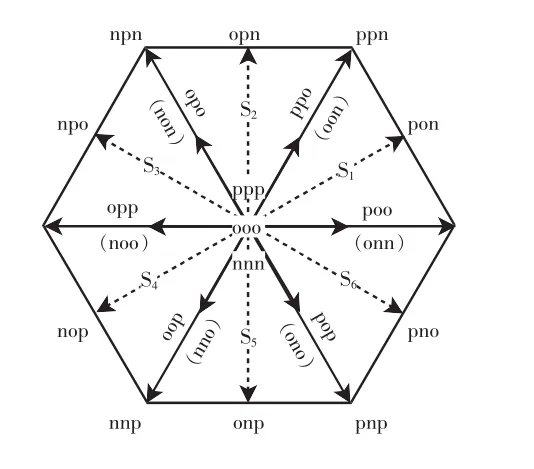
图4 三电平逆变器基本空间矢量Fig.4 Basic space vector diagram of three-level inverter
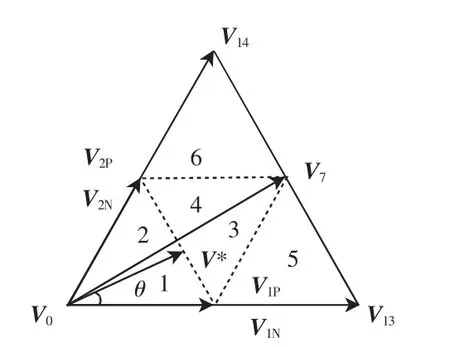
图5 扇区S1的小区划分Fig.5 Partitioning for sector S1
因篇幅有限,图6直接给出了参考矢量位于大区S1小区5时,传统三电平逆变器和Z源三电平逆变器相应的控制时序。图中,T1、T2、T3为合成参考矢量的3个基本矢量的作用时间,T0表示零矢量作用时间。表3为S1大区中6个小区对应的直通矢量状态次序。

图6 传统三电平逆变器和Z源三电平逆变器相应控制时序Fig.6 Timing sequence diagrams corresponding to the traditional and Z-source three-level inverters

表3 扇区S1直通矢量状态次序Tab.3 Sequences of shoot-through vector state in sector S1
2.2 中点电位控制
三电平逆变器在运行过程中必须保证直流侧中点电位的平衡,否则负载中会出现偶次谐波,部分开关器件的电压应力也会增大,不利于逆变器的安全运行[16]。中点电位的不平衡,归根结底是由流入或流出中点的电流造成的,直流侧2个电容1个放电、1个充电,导致中点电位发生偏移[17]。最优SVPWM控制是在传统Z源三电平SVPWM控制基础上,通过调节上、下直通时间来实现中点电位的平衡,没有增加开关损耗。
通过分析,在一个开关周期内,当Z源三电平逆变器处于上直通状态时,其等效电路如图7所示,二极管D1导通,二极管D2承受反相电压截止,逆变桥和负载等效为电流源。由KCL得

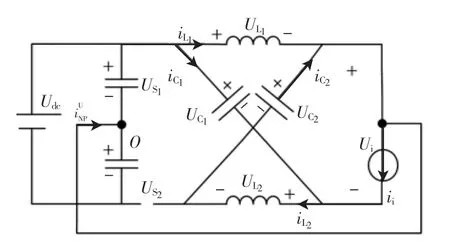
图7 上直通状态等效电路Fig.7 Equivalent circuit in upper shoot-through state
同理,当Z源三电平逆变器处于下直通状态时,其等效电路如图8所示,二极管D2导通,二极管D1承受反相电压截止,逆变桥和负载等效为电流源。由KCL得

式中,为下直通时流出O点的瞬时中线电流。
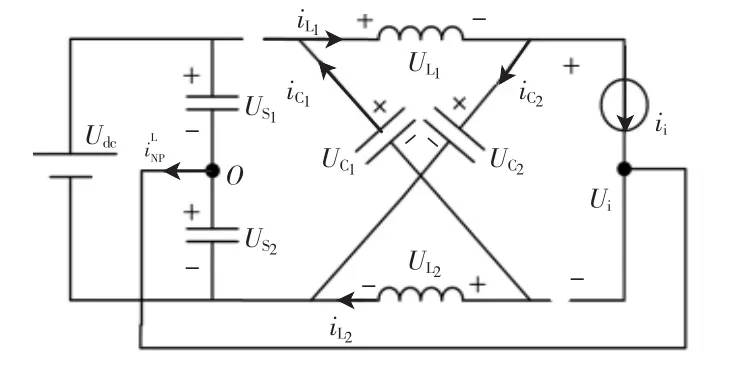
图8 下直通状态等效电路Fig.8 Equivalent circuit in lower shoot-through state
因直通矢量必须插入小矢量状态中才不会影响输出矢量的伏秒值。对于任意小矢量对应的开关状态 sa、sb、sc,令

式中,sx∈{-1,0,1},x∈{a,b,c}。
根据式(4)~式(6)可得

式中:;i∂为线电流。
1个开关周期内的平均中线电流NP为

式中:dx0为各相零状态占空比;Ts为1个开关周期;x为平均线电流,x∈{a,b,c}。
当参考矢量由大、中、小矢量合成时,以图5中扇区S1的小区5为例,根据伏秒平衡原理和直通矢量必须插在正负小矢量中的原则[18]以及式(8)可得

式中:ix为线电流,x∈{a,b,c};dx为基本矢量 Vx中的零状态占空比,x∈{1N,7,1P}。
同理,当参考矢量由小小中矢量合成时,以图5中扇区S1的小区4为例,可得
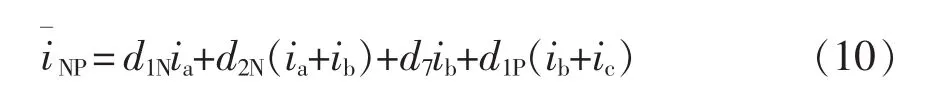
综合式(9)和式(10)可知,1 个开关周期内,如果上、下直通时间相等将不会影响平均中线电流。反之,如果中点电位不平衡,就可以通过调节上、下直通时间来实现中点电位平衡。上直通时,直流侧电容CS1和电容C1、C2同时为两只电感充电,上直通时间越长,CS1电压下降越多。同理,下直通时,直流侧电容CS2和电容C1、C2同时为两只电感充电,下直通时间越长,CS2电压下降越多。
2.3 最优SVPWM控制
根据传统Z源SVPWM控制算法以及上、下直通对中点电位的影响,提出了一种最优SVPWM控制算法。定义ΔU=US1-US2。为了避免中点电位的小波动造成开关频繁动作,定义一个阈值h,即当ΔU>h或者ΔU<-h时才进行调节。施加偏移控制后,上直通时间通过乘以一个调制因子k1来实现,下直通时间通过乘以一个调制因子k2来实现,即

式中,为施加偏移控制后的上、下直通时间,+T'L=2TD。所以,当 ΔU>h 时,k1=0,k2=2;当-h<ΔU<h时,k1=1,k2=1;当 ΔU<-h 时,k1=2,k2=0。
当ΔU>h时,大区S1小区5的控制时序如图9所示,控制原理框图如图10所示。该方法仅需检测2个直流侧电容电压,因此简化了控制系统的设计。

图9 大区S1小区5相应控制时序Fig.9 The corresponding timing sequences in the 5th small space of sector S1
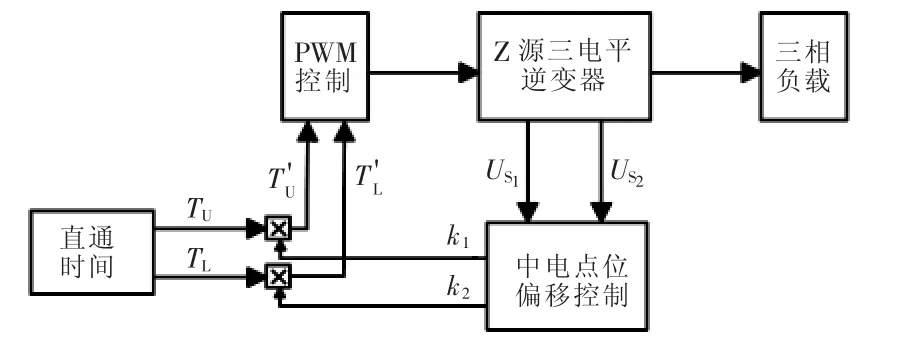
图10 中点电位平衡控制原理框图Fig.10 Block diagram of control principle of neutralpoint potential balance
3 仿真结果比较与分析
为验证该新型结构及优化SVPWM算法的正确性与有效性,使用MATLAB/Simulink搭建了仿真模型。仿真参数如下:直流电源电压Udc为720 V,分压电容 CS1=CS2=100 μF;Z 源电容 C1=C2=220 μF,电感L1=L2=1 mH;开关周期T=0.000 5 s;基波频率为50 Hz;调制比 M=0.6;升压比B=1.25;仿真时间为0.1 s。
不同升压比时系统仿真波形如图11所示,图11(a)、(b) 分别为 B=1.00、B=1.25 时的输出相电压UA、线电压UAB及相电流IA的波形。从图11可以看出,当升压比B=1.00,即系统未升压时,输出相电压UA峰值约为360 V,线电压UAB峰值约为720 V;当升压比B=1.25时,系统输出相电压UA峰值约为445 V,线电压UAB峰值约为890 V,实现升压。
图12所示为新型Z源不对称三电平逆变器的中点电位偏移量波形。由图12(a)可以看出,系统未加中点电位平衡控制时,中点电位波动范围大概在-20 V~30 V 之间;图12(b)为调节上、下直通时间后的中点电位偏移量波形,阈值h=5。可以看出,系统中点电位偏移减小,其波动范围在±5 V以内,有效降低中点电位偏移达83.3%。
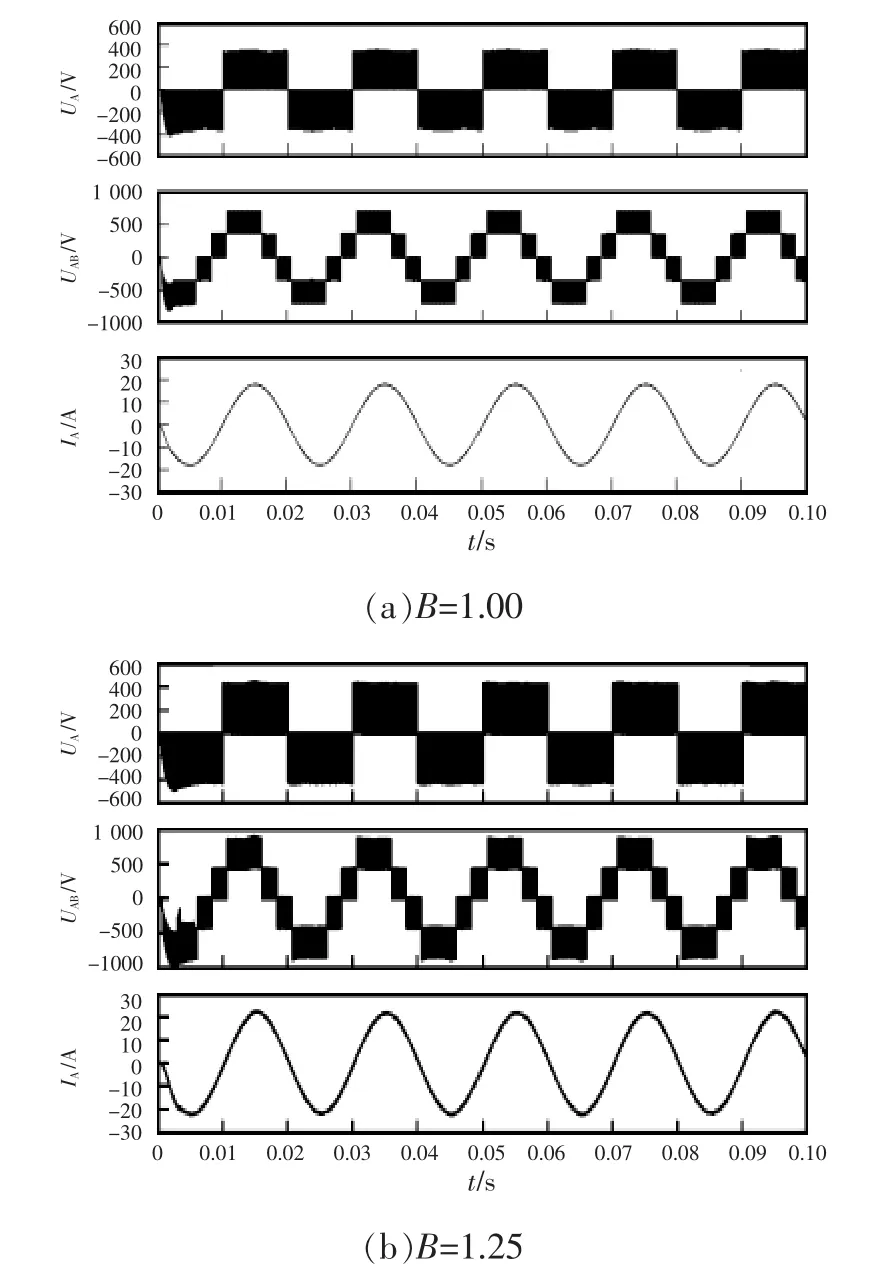
图11 不同升压比时系统仿真波形Fig.11 System simulation waveforms at different values of B

图12 中点电位偏移量波形Fig.12 Waveforms of neutral-point potential offset
图13为传统SVPWM控制与最优SVPWM控制输出电流对应的傅里叶(FFT)频谱分析。由图可以看出,传统SVPWM控制中电流的总谐波畸变率THD(total harmonic distortion)为 1.17%;最优 SVPWM控制中输出电流的THD值为1.22%,与传统SVPWM控制相比相差较小。因此输出电流质量几乎没有因直通矢量的插入以及中点电位控制算法受到影响。
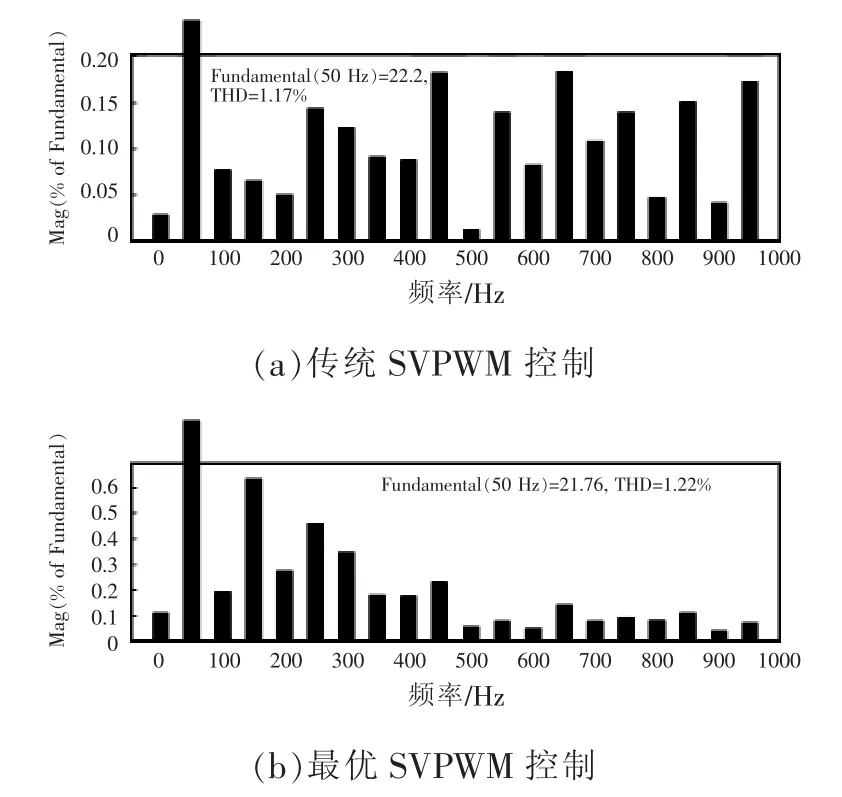
图13 输出电流FFT分析Fig.13 Analysis for the FFT of output current
4 结语
本文提出的新型Z源不对称三电平逆变器拓扑结构不需要箝位二极管,同时保持了Z源三电平的固有优势,提高了系统的经济性和实用性。在实现升压的同时,采用调节上、下直通时间的最优SVPWM算法,最大程度地减少了直通作用产生的开关损耗,并且有效地控制了中点电位偏移,其波动范围控制在±5 V以内。通过仿真结果及分析,验证了其正确性与有效性。
[1]刘凤君.多电平逆变技术及其应用[M].北京:机械工业出版社,2007:156-176.
[2]张瑾,齐铂金.Z源三电平中点钳位逆变器中点电位平衡控制方法[J].中国电机工程学报,2010,30(12):7-13.Zhang Jin,Qi Bojin.Neutral-point potential balancing method for Z-source three-level NPC inverters[J].Proceedings of the CSEE,2010,30(12):7-13(in Chinese).
[3]Nabae A,Takahashi I,Akagi H.A new neutral point clamped PWM inverter[J].IEEE Transaction on Industry Applications,1981,17(5):518-523.
[4]张瑾,齐铂金,张少如.Z源三电平中点钳位逆变器的空间矢量调制方法[J].电工技术学报,2010,25(9):108-114.Zhang Jin,Qi Bojin,Zhang Shaoru.A space vector-PWM algorithm for Z-Source three-level NPC inverters[J].Transactions of China Electrotechnical Society,2010,25 (9):108-114(in Chinese).
[5]Loh P C,Vilathgamuwa D M,Lai Y S.Pulse-width modulation of Z-source inverters[J].IEEE Transactions on Power Electronics,2005,20(6):1346-1355.
[6]彭方正,房绪鹏,顾斌,等.Z源变换器[J].电工技术学报,2004,19(2):47-51.Peng Fangzheng,Fang Xupeng,Gu Bin,et al.Z-source converter[J].Transactions of China Electrotechnical Society,2004,19(2):47-51(in Chinese).
[7]Peng Fangzheng.Z-source inverter[J].IEEE Transactions on Industry Applications,2003,39(2):504-510.
[8]张成,孙驰,马伟明,等.基于电路拓扑的IGBT并联均流方法[J].高电压技术,2013,39(2):505-512.Zhang Cheng,Sun Chi,Ma Weiming,et al.Paralleling current sharing method of parallel IGBTs based on circuit topology[J].High Voltage Engineering,2013,39(2):505-512(in Chinese).
[9]黄珂,魏金成,黄容容,等.一种新型不对称三相三电平逆变器[J].电源技术,2014,38(5):920-923.Huang Ke,Wei Jincheng,Huang Rongrong,et al.A novel three-phase three-level inverter with asymmetrical legs[J].Chinese Journal of Power Sources,2014,38(5):920-923(in Chinese).
[10]Song Qiang,Liu Wenhua,Yu Qingguang,et al.A neutralpoint potential balancing algorithm for three-level NPC inverters using analytically injected zero-sequence voltage[C].Applied Power Electronics Conference and Exposition,2003, APEC’03.Miami Beach,USA,2003,1:228-233.
[11]王展,邹云屏,林磊,等.一种三电平逆变器中点平衡的控制方法[J].电源学报,2004,2(4):287-291.Wang Zhan,Zou Yunping,Lin Lei,et al.A control method of neutral-point voltage balancing problem in three-level inverters[J].Journal of Power Supply,2004,2(4):287-291(in Chinese).
[12]Newton C,Sumner M.A novel arrangement for balancing the capacitor voltages of a five-level diode clamped inverter[C].1998 Seventh International Conference on Power Electronics and Variable Speed Drives.London,UK,1998:465-470.
[13]贺昱曜,冯伟,宋石磊.Z源级联三电平中点钳位逆变器[J].电网技术,2012,36(4):219-224.He Yuyao,Feng Wei,Song Shilei.A cascaded Z-source three-level neutral point clamped inverter[J].Power System Technology,2012,36(4):219-224(in Chinese).
[14]Loh P C,Gao Feng,Blaabjerg F,et al.Operational analysis and modulation control of three-level Z-source converters with enhanced output waveform quality[J].IEEE Transactions on Power Electronics,2009,24(7):1767-1775.
[15]牛清泉,屈克庆.一种基于Z源三电平逆变器的SVPWM算法研究[J].电网与清洁能源,2012,28(12):23-29.Niu Qingquan,Qu Keqing.Study on SVPWM method based on Z-source three-level inverters[J].Power System and Clean,2012,28(12):23-29(in Chinese).
[16]张志,谢运祥,乐江源,等.消除中点电位低频振荡的三电平逆变器空间矢量脉宽调制方法[J].电工技术学报,2011,26(3):103-109.Zhang Zhi,Xie Yunxiang,Le Jiangyuan,et al.SVPWM method of removing the low-frequency oscillations of neutral point voltage for three-level NPC inverter[J].Transactions of China Electrotechnical Society,2011,26(3):103-109(in Chinese).
[17]符晓.电励磁同步电机低开关频率控制技术研究[D].徐州:中国矿业大学,2011.Fu Xiao.Control of electrical excited synchronous machine at low switching frequency[D].Xuzhou:China University of Mining and Technology,2011(in Chinese).
[18]付文波.多电平Z源逆变器脉宽调制及应用研究[D].徐州:中国矿业大学,2015.Fu Wenbo.Research on pulse width modulation and application for multilevel Z-source inverter[D].Xuzhou:China U-niversity of Mining and Technology,2015(in Chinese).
