一种降低电网谐波影响的单相自适应锁频方案

张博文，王 萍，贝太周

（1.天津大学电气自动化与信息工程学院智能电网教育部重点实验室，天津300072；2.国网济南供电公司，济南 250012）

随着新能源发电技术的不断发展，太阳能、风能等清洁能源需要通过可靠的技术产生可利用的电能[1-4]。分布式电源与环境相融合，发电方式灵活等特点给当代电力系统带来了巨大变化[5-6]。为了确保分布式电源向电网提供可靠的电能，近年来，多种新型的并网控制策略被相继提出[7-8]。在并网控制策略的具体实现中，如何通过电网同步技术准确获取电网电压的频率或相位成为关键性的问题[4]。在实际电网环境下，电网故障和非线性负载的变化通常会导致电网电压严重的谐波畸变以及频率波动[9]。因此，在实际电网出现谐波畸变和频率突变的应用场合下，采用准确可靠的电网同步方案是保证逆变器有效并网的可靠前提[10]。

单相逆变器相较三相逆变器而言，电网电压所包含的信息更少，因此数字锁相更加困难。近年来，很多适用于单相并网逆变器的同步方案被相继提出。其中，基于同步旋转坐标变换的方法具有动态性能好的优点，但是往往需要经过两次坐标变换，运算量较大[10]；基于过零点检测的锁相方法对输入信号谐波或扰动较为敏感且实时性较差，当电网电压含有谐波、毛刺情况下会存在多个过零点，以致锁相失败，但其原理简单、易于实现，可用于电网电压波形质量较好的工业实践中[11-12]；在单相系统中，基于二阶广义积分正交信号发生器SOGI-QSG（second-order generalized integrator-quadrature signal generator）发展起来的电网同步方案成为近几年的研究热点[11,14,17]。

本文在级联SOGI-QSG结构[13]基础上提出一种自适应锁频方案。该方案具有结构简单、动态响应速度快的优点，当电网电压出现严重畸变时，借助该方案可以准确地估量出基波电压信号的频率以及幅值。

1 级联SOGI-QSG及滤波特性

1.1 单一SOGI-QSG结构

借助SOGI-QSG可以将单相输入信号转换成两相相位差90°的输出信号，同时可以有效滤除输入信号中的谐波分量。传统SOGI-QSG结构[14]如图1所示。图1中，k和ω0分别为该结构的增益系数和中心角频率，v为输入信号，v'与qv'为输出信号，其中qv'滞后v'的相位角为90°。

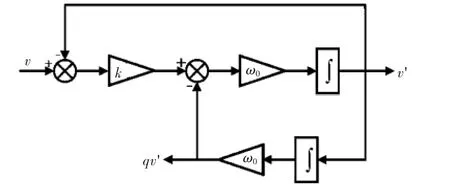
图1 传统SOGI-QSG结构Fig.1 Structure of conventional SOGI-QSG

根据图1，传统SOGI-QSG的传递函数为

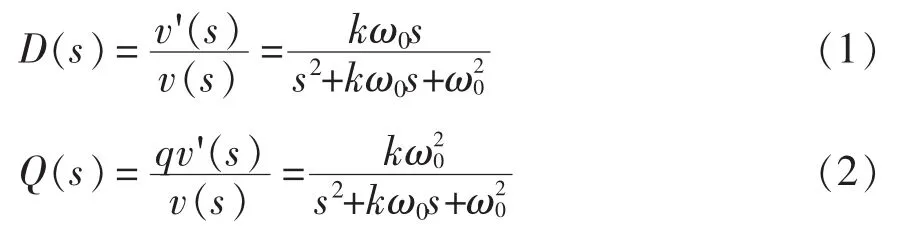
当 k 取不同值 （k1=0.4，k2=1.4，k3=5.0），ω0=314 rad/s时，传递函数 D（s）和 Q（s）的 bode 图分别如图2和图3所示。

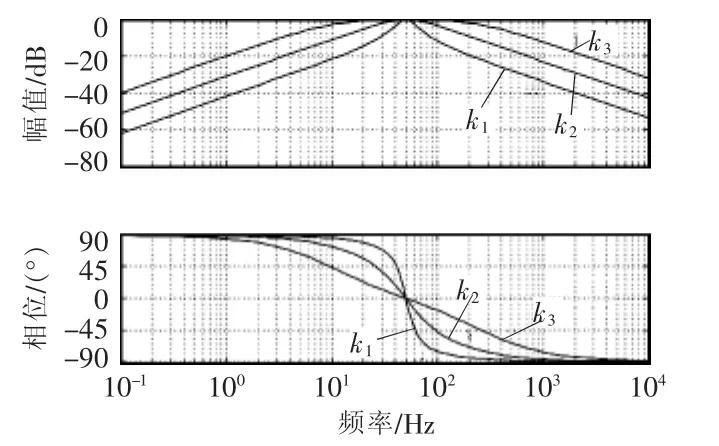
图2 k取不同值时传递函数D（s）的Bode图Fig.2 Bode diagram of transfer function D（s） with different values of k

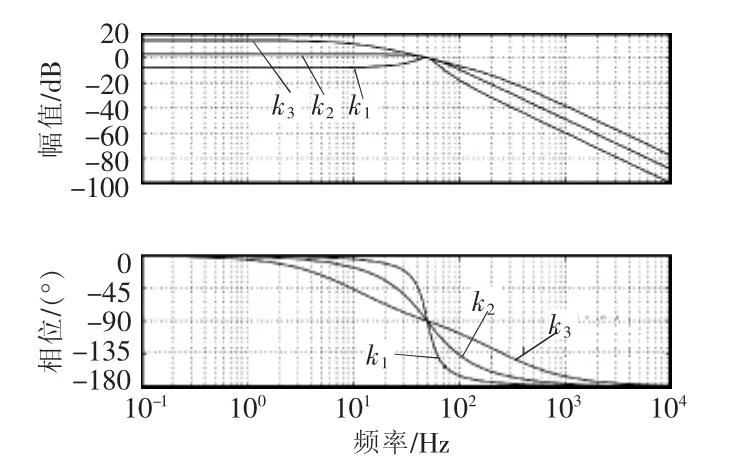
图3 k取不同值时传递函数Q（s）的Bode图Fig.3 Bode diagram of Q（s） with different values of k

根据图2 和图3，D（s）和 Q（s）分别呈现出带通滤波和低通滤波的作用。相位上，在中心角频率ω0处，输出信号v'不存在相位偏移，而qv'滞后输入信号90°，输出信号的幅值与输入信号幅值之间不存在幅值衰减的影响。系统的滤波性能与增益系数k的取值有关。从图2和图3中可以看出，k的取值越大，滤波性能越差，系统的响应速度同样依赖于k。根据SOGI-QSG 系统响应的整定时间 ts=9.2/（kω0）[15]，若 k变大，响应速度则变小。当ω0=314 rad/s、增益系数k=时，系统整定时间约为20 ms，二阶系统阻尼系数，此时整定时间和动态响应超调之间的关系最优[16]。

1.2 级联SOGI-QSG结构

由图2和图3可以进一步发现，对输入信号中的高频谐波而言，Q（s）会表现出更好的滤波效果。基于这一客观事实，本文采用如图4所示的级联SOGI-QSG结构。该结构将前级SOGI-QSG的输出qv'作为后级SOGI-QSG的输入。级联SOGI-QSG除了具有更好的滤波效果外，借助后级SOGI-QSG的相位偏移特性便于在αβ坐标系下实现电网频率的自适应调整。当电网频率改变时，通过频率自适应控制器及时对SOGI-QSG的中心频率进行补偿，同时提取出瞬时的电网频率。

根据式（1）、式（2）和图4，可以得出级联 SOGIQSG的频域传递函数为

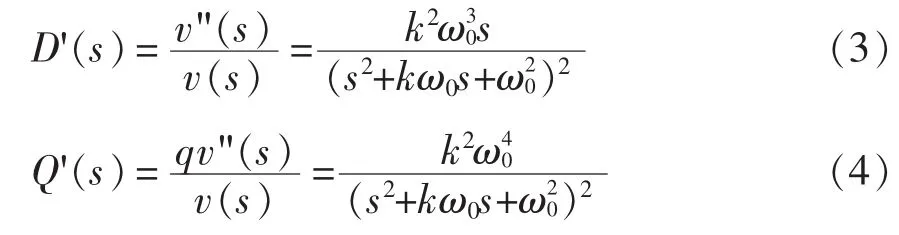
当 k=1.414、ω0=314 rad/s 时，传递函数 D'（s）和Q'（s）的 bode 图如图5所示。由图5 可见，D'（s）和Q'（s）对输入信号中高频谐波的衰减率分别为-60 dB/dec和-80 dB/dec，该数据证实了采用的级联SOGI-QSG结构具有较强的滤波性能。另外，D'（s）和Q'（s）分别表现为带通滤波和低通滤波的效果。特别地，当中心角频率等于电网基波频率时，级联SOGI-QSG结构可以准确估量出电网基波信号，并可有效滤除大量高频谐波。输出信号v"和qv"分别滞后输入信号v的电角度为90°和180°。

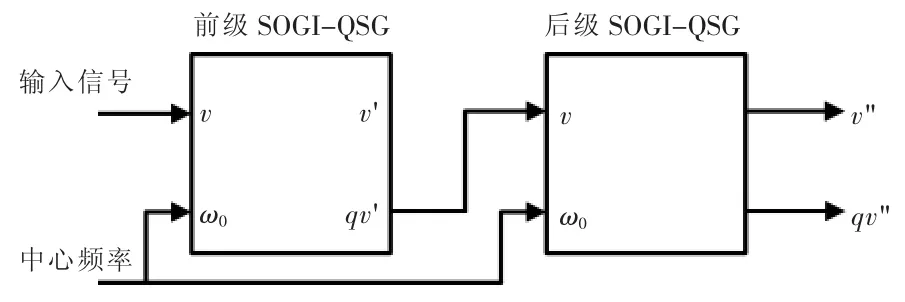
图4 级联SOGI-QSG结构Fig.4 Structure of the cascaded SOGI-QSG

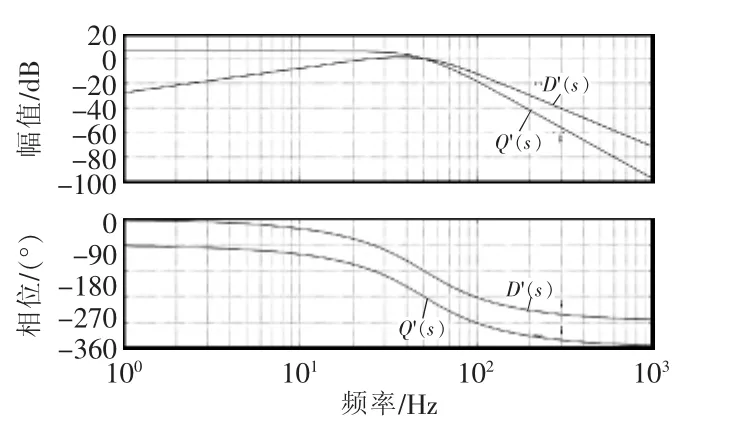
图5 传递函数D'（s）和Q'（s）的Bode图Fig.5 Bode diagram of transfer functions D'（s）and Q'（s）

设含有谐波的电网电压为

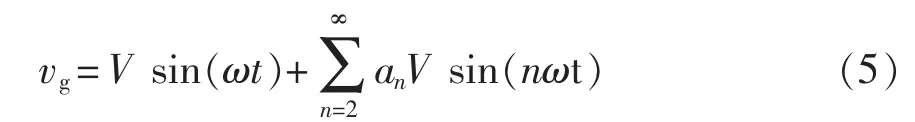
式中：V为基波电压幅值；an为电网电压n次谐波所占百分比。

为了验证级联SOGI-QSG较强的滤波性能，通过Matlab对级联SOGI-QSG进行仿真。设输入电压信号基波幅值为V，频率为50 Hz，输入信号中含有的多次谐波，同时通过级联SOGI-QSG滤波后得到各个信号中所含谐波的百分比与THD值，如表1所示。

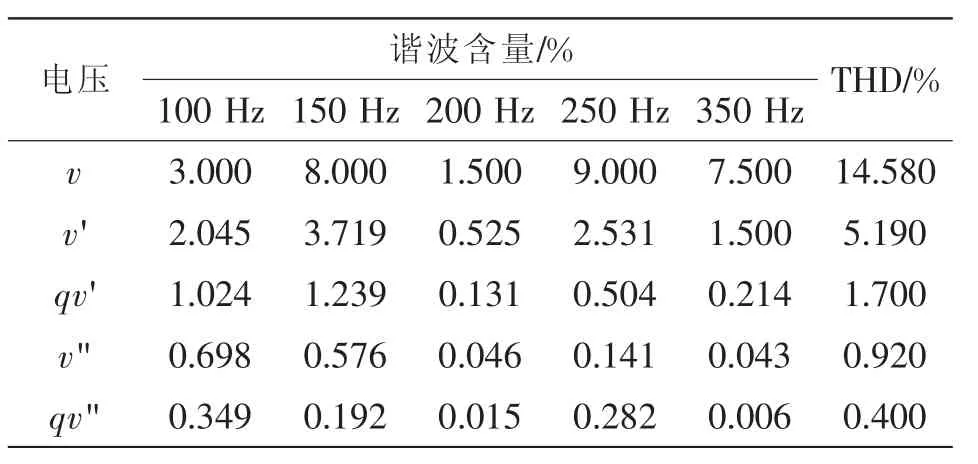
表1 级联SOGI-QSG的输入、输出信号成分对比Tab.1 Composition of input and output signals of the cascaded SOGI-QSG

从表1可以看出，通过级联SOGI-QSG滤波后，各输出信号中的谐波含量得到明显降低。

2 频率自适应控制器

式（1）和式（2）所描述的频域传递函数的幅相特性分别为

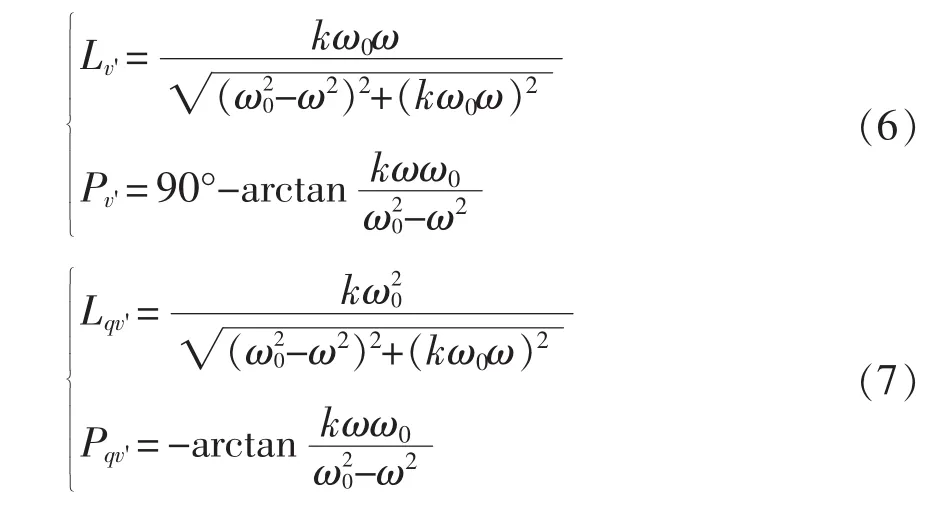
式中：Lv'和Lqv'为相应的幅值增益系数；Pv'和Pqv'为相应的相位偏移度；ω为电网频率。考虑级联SOGIQSG，由式（3）、式（4）与式（6）、式（7）可以看出：当ω0=ω时，输出信号不会出现幅值上的衰减以及相位上的偏移；而ω0≠ω时，级联SOGI-QSG的输出信号不仅会出现幅值上的衰减，而且还有相位上的偏差。在实际电网中，电网频率多会出现波动，为了保证级联SOGI-QSG可以在实际电网中正常工作，需要依靠性能良好的自适应锁频算法对输入信号的频率进行有效跟踪。

级联SOGI-QSG结构中，前级SOGI-QSG的输出为

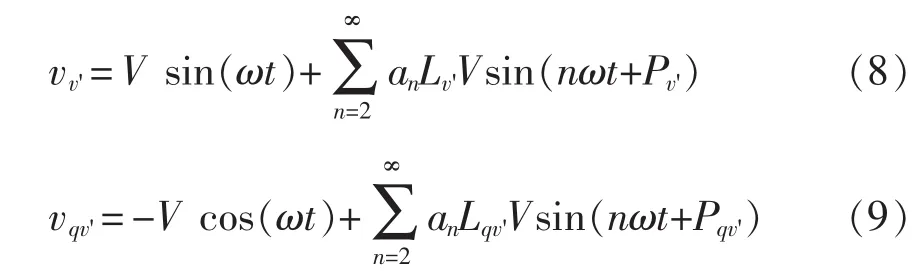
后级SOGI-QSG的输出为

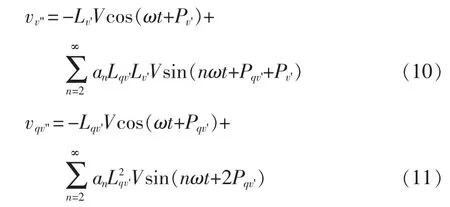
结合式（7）～式（11），将以上 4 个输出信号分别单位归一化后，定义频率自适应控制律为

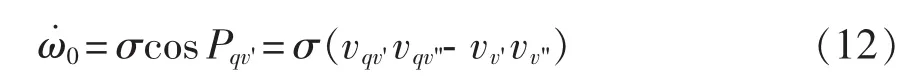
式中，σ为频率调整因子。

根据式（7）中Pqv'的表达式，可做出关于Pqv'的三角函数关系，如图6所示。

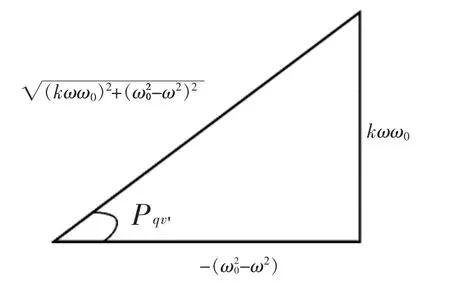
图6 关于Pqv'的三角函数关系Fig.6 Trigonometric relationship of Pqv'

特别地，当ω0无限趋近于ω时，根据式（12）和图6，可推出

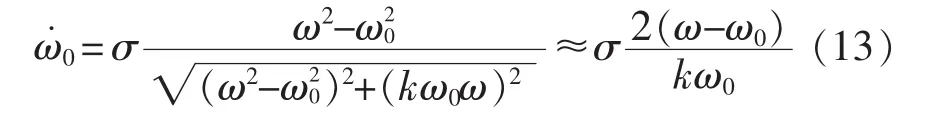
因此，基于级联SOGI-QSG构成的自适应锁频控制器的形式简单描述为

式（14）有唯一的局部平衡点，且当 ω＞ω0时ω˙0＞0；当ω＜ω0时ω˙0＜0，因此通过式（14）即可保证 ω0总是朝着减小频率检测误差的方向运动。根据式（10）～式（14）的推导过程可以判定，式（12）定义的频率自适应控制律能够实现对级联SOGI-QSG频率的跟踪。系统的时间常数为 τ=（kω0）/（2σ）， 而按照 IEEE Std.1574的规定，实际电网频率可在-0.7～0.5 Hz范围内波动，电网电压频率严重波动的范围为±3 Hz。因为对时间常数τ而言，实际的电网频率波动对τ的影响很小，所以本文所提出的频率自适应环节的响应速度基本不受实际电网电压频率波动的影响。

综合以上阐述，本文所提的频率自适应系统的结构框图如图7所示。

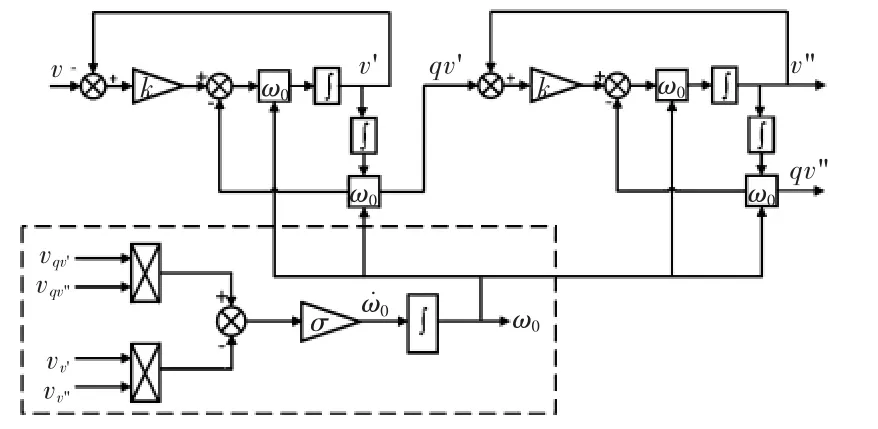
图7 频率自适应控制器框图Fig.7 Block diagram of frequency adaptive controller

3 仿真与实验验证

3.1 仿真实验

为了验证本文提出的基于级联SOGI-QSG的自适应锁频方案的性能，利用Matlab/Simulink软件平台搭建单相并网逆变系统，进而对其性能进行验证。系统输入信号参数如表1所示，其中基波电压频率为50 Hz、幅值为，级联SOGI-QSG的增益系数k取值为，设 ω0=314 rad/s，取 σ=88 799.2，计算出时间常数τ≈2.5 ms，频率响应时间为（3～5）τ，即在 10 ms左右。

图8为输入信号v和级联SOGI-QSG的输出信号v"和qv"的波形。从图8中可以看出：输出信号v"和qv"分别滞后输入信号v的相角为90°和180°，通过级联SOGI-QSG可以准确地从严重畸变的信号中提取出基波信号。

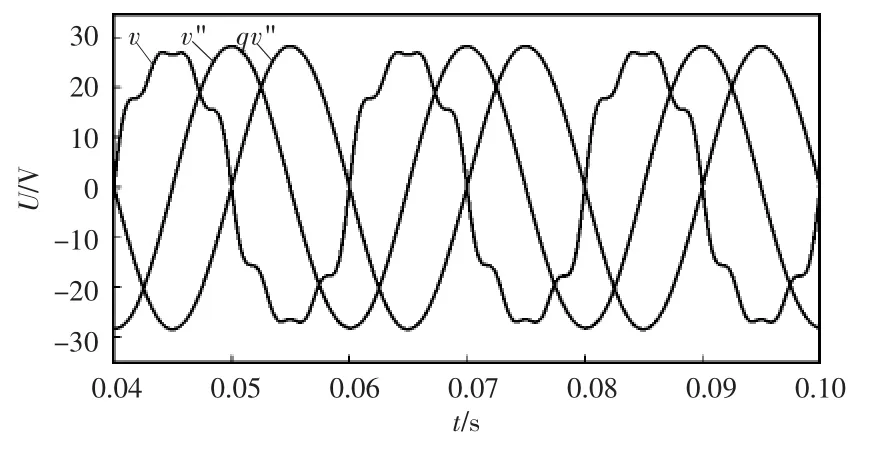
图8 级联SOGI-QSG输入信号、输出信号波形Fig.8 Waveforms of input and output signals of the cascaded SOGI-QSG

图9为0.06 s时输入信号v从降到20 V时，级联SOGI-QSG的输出信号v"和qv"的图像。图中输入、输出信号上方的直线是输入基波信号幅值标定线。从图9中可以看出：随着输入信号的改变，级联SOGI-QSG的输出信号在0.06 s时产生波动，由于在滤波过程中SOGI-QSG本身存在响应时间[16]，在0.1 s左右通过级联SOGI-QSG可以准确地估量到一组与输入基波信号幅值相等的输出信号v"和 qv"，v"和 qv"的相角差为 90°。即通过级联SOGI-QSG可以准确估量单相电网电压幅值。

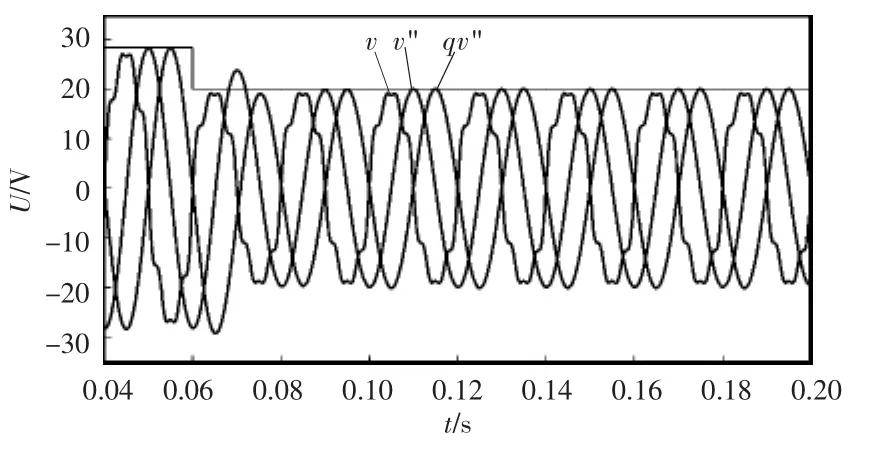
图9 改变输入信号时级联SOGI-QSG输出波形Fig.9 Waveforms of output of the cascaded SOGI-QSG in the case of changing the input signal

图10为频率自适应方案的仿真结果。在图10（a）中，原输入信号v基波幅值在0.06 s时从V降到20 V；在0.1 s时其频率从50 Hz降到48 Hz。图10（b）为频率自适应控制器的响应过程。为了更好地体现所提出基于级联SOGI-QSG的频率自适应系统的快速性和准确性，与文献[17]中的单相SOGIFLL系统做出对比。从图10（b）中可以看出：在0.6 s时刻基波幅值改变时，频率自适应控制器无波动；在0.1 s基波频率从50 Hz变为48 Hz时，本论文所提出频率自适应控制器在10 ms左右的时间内对其进行频率跟踪。对比文献[17]所提SOGI-FLL系统的仿真结果，本文所提出频率自适应系统的响应速度更快，阻尼响应效果更平顺。通过仿真，验证了所提出基于级联SOGI-QSG的频率自适应系统不受基波幅值改变的影响，具有很好的鲁棒性；同时可以快速、准确地跟踪基波频率。

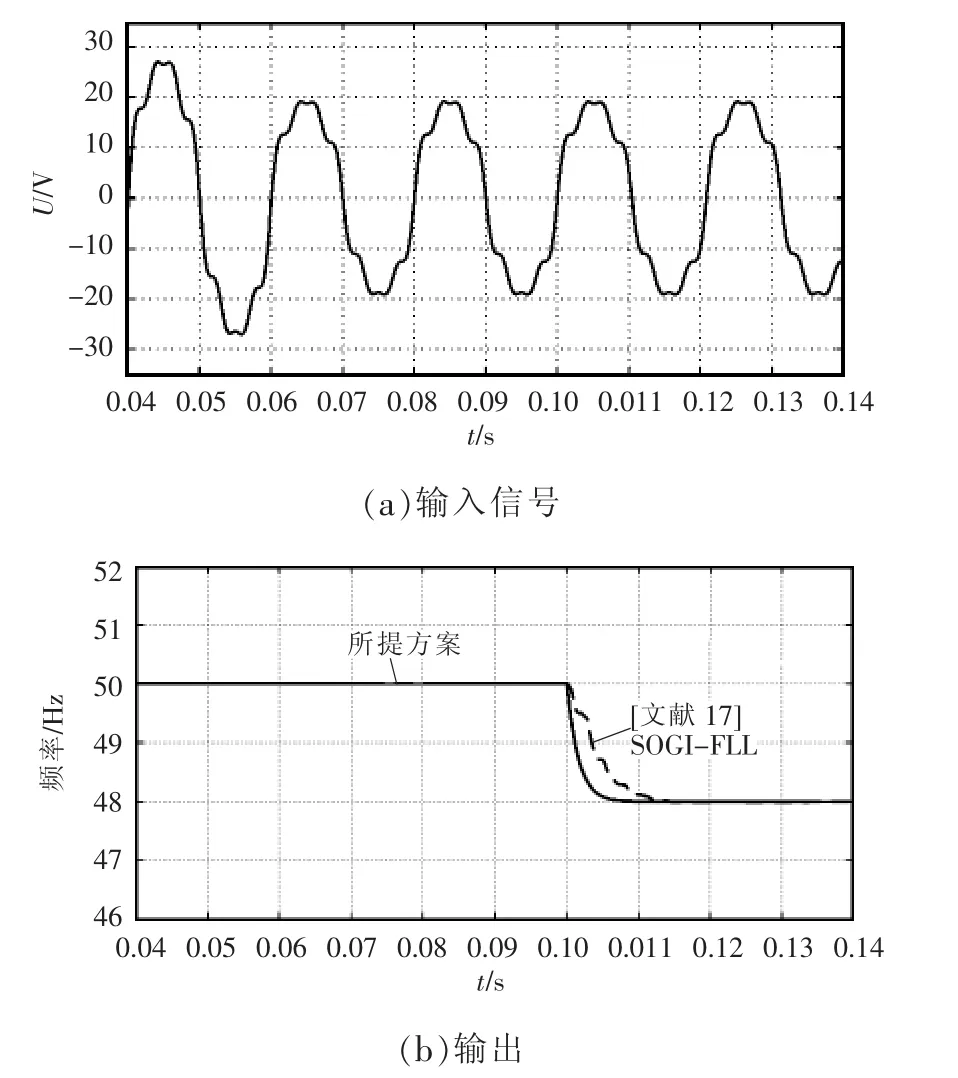
图10所提频率自适应方案的输入、输出波形Fig.10 Input and output waveforms using the proposed frequency adaptive scheme

3.2 实验验证

为验证本文所提的自适应锁频方案的有效性，现对该方案进行实验验证。实验中处理器选用型号为TMS320F28335的DSP，主要实验设备包括可编程交流电源、电压传感器和示波器。产生的单相交流输入电压信号的各次谐波含量如表1所示，基波电压幅值为，频率为50 Hz。级联SOGIQSG的增益系数，频率自适应调整系数σ设定为88 799.2。

图11为输入电压信号v通过级联SOGI-QSG滤波器后得到的输出信号v"、qv"。从图中可以看出级联SOGI-QSG在稳态输出情况下，两相电压幅值均为，相位相差90°，并且具有较高的正弦度，因此可以说明级联的SOGI-QSG可以很好地降低谐波的影响，从畸变严重的输入信号中准确提取出基波分量。

图12为输入电压信号幅值从跌落到20 V、电网频率从50 Hz跌落到48 Hz时，自适应锁频方案的响应结果。从图中可以发现，所提方案仅用10 ms的时间便可完成对电网频率的有效跟踪，实验结果与第3.1节的仿真结果一致。

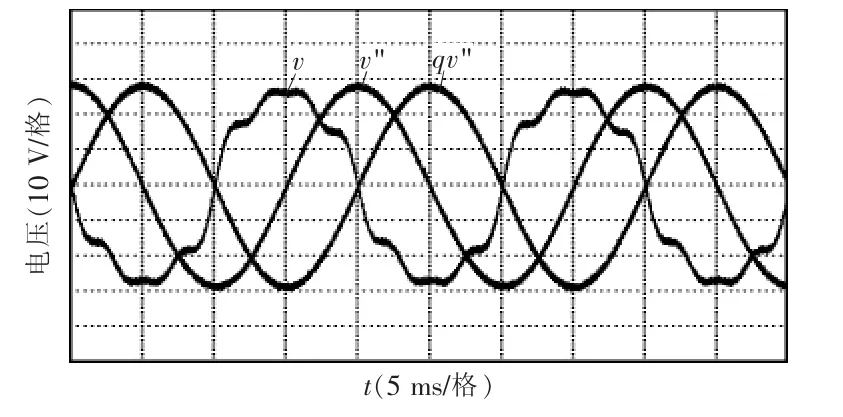
图11 级联SOGI-QSG的输出波形Fig.11 Waveforms of output of the cascaded SOGI-QSG

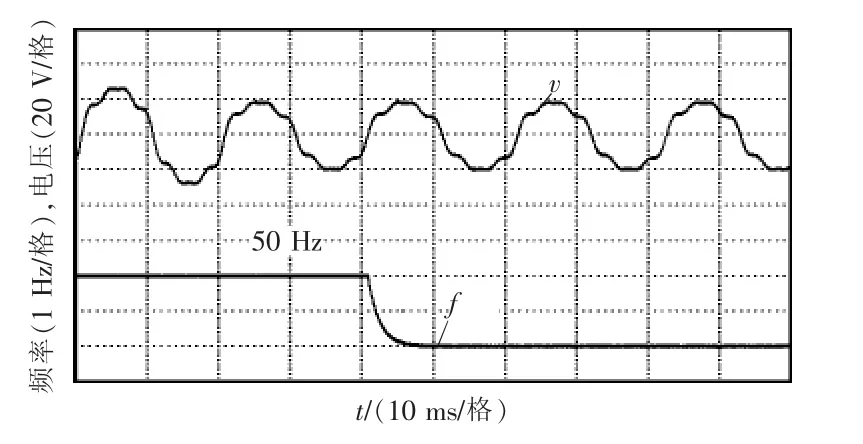
图12 频率突变时的锁频结果Fig.12 Frequency-locked results in the case of changing frequency

4 结语

本文针对含有谐波的单相并网领域，对自适应锁频问题展开研究，提出一种基于级联SOGI-QSG结构的单相自适应锁频方案。对该方案中涉及的滤波性能和频率检测的响应问题做了理论分析和实验验证，由此得到以下结论。

（1）所提出的方案具有良好的滤波性能，可以应用在电网电压严重畸变的单相并网系统中。

（2）所提出的方案可以准确快速地跟踪实际的电网频率，本方案的响应时间为10 ms。

（3）所提出的方案不受电网基波幅值的影响，系统具有较强的鲁棒性。

[1]徐德鸿,陈文杰,何国锋,等.新能源对电力电子提出的新课题[J].电源学报,2014,12（6）:4-9.Xu Dehong,Chen Wenjie,He Guofeng,et al.New power electronics topics brought by the development of renewable energy[J].Journal of Power Supply,2014,12（6）:4-9（in Chinese）.

[2]Bei Taizhou,Wang Ping,Yang Liu,et al.Dynamic sliding mode evolution PWM controller for a novel high-gain interleaved DC-DC converter in PV system[J].Journal of Applied Mathematics,2014,10:1-11.

[3]Blaabjerg F,Liserre M,Ma K.Power electronics converters for wind turbine systems[J].IEEE Transactions on Industry Applications,2012,49（2）:708-719.

[4]贝太周,王萍,蔡蒙蒙.注入三次谐波扰动的分布式光伏并网逆变器孤岛检测技术[J].电工技术学报,2015,30（7）:44-51.Bei Taizhou,Wang Ping,Cai Mengmeng.An islanding detection method with the third harmonic injection for distributed grid-connected PV inverters[J].Transactions of China Electrotechnical Society,2015,30（7）:44-51（in Chinese）.

[5]袁庆庆,伍小杰,石祥龙,等.基于特定谐波消除的并网锁相环技术[J].中国电机工程学报,2013,33（36）:34-40.Yuan Qingqing,Wu Xiaojie,Shi Xianglong,et al.Gridconnected phase locked loop based on selective harmonic elimination[J].Proceedings of the CSEE,2013,33（36）:34-40（in Chinese）.

[6]王萍,王尉,贝太周,等.数字控制对并网逆变器的影响及抑制方法[J].天津大学学报：自然科学与工程技术版,2016,49（5）:472-479.Wang Ping,Wang Wei,Bei Taizhou,et al.Effects of digital control on grid-connected inverter and its suppression method[J].Journal of Tianjin University：Science and Technology,2016,49（5）:472-479（in Chinese）.

[7]Wang Liang,Jiang Qirong,Hong Lucheng,et al.A novel phase-locked loop based on frequency detector and initial phase angle detector[J].IEEE Transactions on Power Electronics,2013,28（10）:4538-4549.

[8]樊英,张丽,薛钟兵,等.基于V2G的无功功率补偿技术[J].电网技术,2013,37（2）:307-311.Fan Ying,Zhang Li,Xue Zhongbing,et al.Reactive compensation technology based on vehicle to grid[J].Power System Technology,2013,37（2）:307-311（in Chinese）.

[9]周鑫,陈宏钧,刘博,等.快速且谐波不敏感的电网电压同步方法[J].中国电机工程学报,2015,35（9）:2194-2201.Zhou Xin,Chen Hongjun,Liu Bo,et al.A fast and harmonics-insensitive grid voltage synchronization method[J].Proceedings of the CSEE,2015,35（9）:2194-2201（in Chinese）.

[10]陶兴华,李永东,孙敏,等.一种基于同步旋转坐标变换的单相锁相环新算法[J].电工技术学报,2012,27（6）:147-152.Tao Xinghua,Li Yongdong,Sun Min,et al.A novel singlephase locked loop algorithm based on synchronous reference frame[J].Transactions of China Electrotechnical Society,2012,27（6）:147-152（in Chinese）.

[11]Bei Taizhou,Wang Ping.Robust frequency-locked loop algorithm for grid synchronization of single-phase applications under distorted grid conditions[J].IET Generation,Transmission&Distribution,2016,10（11）:2593-2600.

[12]王宝诚,伞国成,郭小强,等.分布式发电系统电网同步锁相技术[J].中国电机工程学报,2013,33（1）:50-55.Wang Baocheng,San Guocheng,Guo Xiaoqiang,et al.Grid synchronization and PLL for distributed power generation systems[J].Proceedings of the CSEE,2013,33（1）:50-55（in Chinese）.

[13]庞科旺,包其仕.逆变器在电网故障下的并网同步化技术[J].电测与仪表,2015,52（21）:40-43.Pang Kewang,Bao Qishi.Grid-connected synchronization method for inverters under grid fault conditions[J].Electrical Measurement&Instrumentation,2013,33（1）:50-55（in Chinese）.

[14]Golestan S,Freijedo F D,Guerrero J M.A systematic approach to design high-order phase-locked loops[J].IEEE Transactions on Power Electronics,2015,30（6）:2885-2890.

[15]Matas J,Castilla M,Miret J,et al.An adaptive prefiltering method to improve the speed/accuracy tradeoff of voltage sequence detection methods under adverse grid conditions[J].IEEE Transactions on Industrial Electronics,2014,61（5）:2139-2151.

[16]Teodorescu R,Liserre M,Rodriguez P.光伏与风力发电系统并网变换器[M].周克亮,王政,徐青山,译.北京:机械工业出版社,2012:67-73.

[17]Rodriguez P,Luna A,Candela I,et al.Grid synchronization of power converters using multiple second order generalized integrators[C].34th Annual Conference of IEEE Industrial Electronics,2008 IECON,2008:755-760.