基于小交流信号下垂的微网二次控制方法

武 腾，刘 增，刘进军，刘宝谨，王施珂

（西安交通大学电气工程学院，西安 710049）

微网是一个集成了分布式发电、分布式储能以及负载的电能系统，它可以工作于并网模式和孤岛模式[1-6]。在很多情况下，分布式电源以电力电子器件，比如逆变器，作为接口与公共交流母线相连[6-8]，因此，微网中并联逆变器的控制尤显重要。

当微网中分布式电源的地理位置和传输线上的干扰限制了通讯线的应用时，下垂控制[2,9,10]可以在不依赖通讯线的情况下实现并联逆变器间的协调控制，因此，其被广泛应用于微网中分布式电源的控制。然而，传统的下垂控制会导致逆变器的输出电压在幅值和频率上存在偏差[11]。为了消除这种偏差，很多文献中都提出了改进的控制方法[11-15]。虽然这些改进的方法可以在一定程度上恢复电压幅值和频率，但是它们也会带来一些弊端。文献[11]中提出了一种基于虚拟功率流的下垂控制方法，但是该方法不能有效消除电压幅值上的偏差；文献[12]利用比例控制器进行二次控制，但是该方法在稳态下无法实现电压幅值和频率的完全恢复；文献[13]中提出了一种基于负载估算的二次控制方法，该方法在有效恢复电压幅值和频率的同时，又能实现并联逆变器间的功率均分，然而该方法对盲区的依赖使二次调整变得相对缓慢；文献[14]中提出的二次控制方法通过动态改变主电源的下垂特性来实现频率的恢复，但是该方法对主电源的容量要求很高，因此在很多实际的工程场合中并不适用；文献[15]中利用中央控制器进行分层控制，但是该方法对中央控制器的依赖降低了其可靠性；文献[16]中通过利用分布式二次控制器提高了系统的可靠性，但是参数的微小差异会导致该方法无法实现并联逆变器间的功率均分，并且该方法对通讯线的依赖降低了系统的分布性，提高了成本和对线路上噪音的敏感性。

为了克服文献[16]中分布式二次控制的缺陷，受文献[17]中方法的启发，本文提出了一种新型的无互联线的二次控制方法，该方法通过建立向系统内注入一个小交流信号以协助二次控制，在小交流信号的频率和逆变器输出基波电压的下垂偏置之间建立下垂关系，以实现并联逆变器在二次调整过程中的同步。同时，系统频率和电压幅值由比例积分（PI）控制器调节。该方法不仅可以准确恢复电压幅值和频率，而且可以在无互联线的情况下快速实现并联逆变器间的功率均分。仿真和实验结果都验证了该方法的有效性。

1 传统下垂控制方法

在高电压或中电压等级的微网中，传输线阻抗中的感性成分占主导，微网中接交流母线的逆变器等效电路如图1所示。因此图中2个电压E∠φ和UL∠0之间的功率流动服从以下关系[10]，即

式中：E和UL分别为逆变器的输出电压和公共连接点 PCC（point of common coupling）电压；P 和 Q 分别为从逆变器流向负载的有功功率和无功功率；φ为E和UL的相位差；Z为线路阻抗；θ为线路阻抗角。

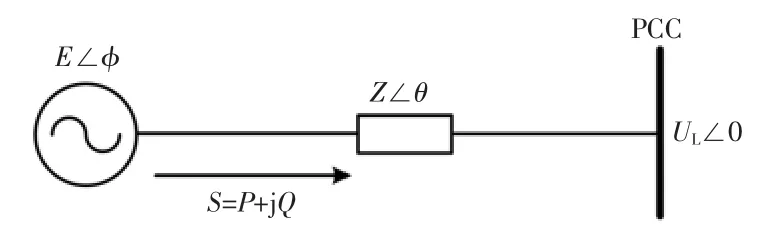
图1 微网中接交流母线的逆变器等效电路Fig.1 Equivalent circuit of an inverter connected to the AC bus of microgrid

基于式（1）和式（2），利用 P-ω 和 Q-V 下垂关系控制频率和电压幅值[2,9,13]，从而实现负载所需功率的均分。下垂控制的数学表达式为

式中：ω*和E*分别为生成的频率和电压幅值的指令；P0和Q0分别为基波电压的下垂偏置；m和n为下垂系数，定义为正。

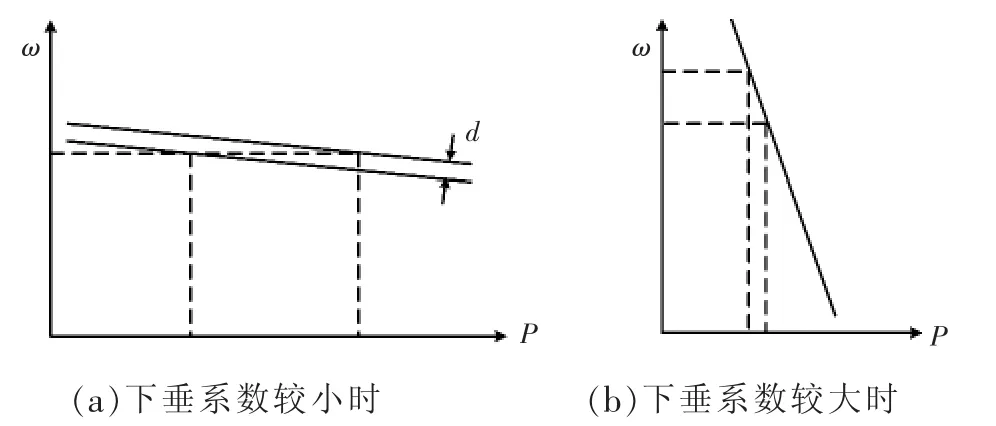
图2 下垂系数设计Fig.2 Design of different droop coefficients

下垂控制可以在无互联线的情况下实现并联逆变器间的功率均分，但是其中也存在功率均分精度和电压调整率之间的折中问题，如图2所示。由于控制或硬件参数的不同，2台逆变器的下垂特性很难完全一致，下垂特性曲线间存在微小的差异d。当下垂系数设计得较小时，功率均分精度会降低，如图2（a）所示；相反，当下垂系数设计得较大时，负载的微小变动会导致逆变器输出电压幅值和频率出现较大的波动，如图2（b）所示，这是不利于系统稳定的。

工程实际中，为了取得较高的功率均分精度，下垂系数需要设计得较小，这就需要通过一定的控制手段将逆变器输出电压的幅值和频率恢复至额定值。

2 新型二次控制方法

2.1 基本思路

图3所示为本文所提方法的N台逆变器并联微网简化示意，所有变流器的一次控制都为下垂控制，控制方程如式（3）和式（4）所示。

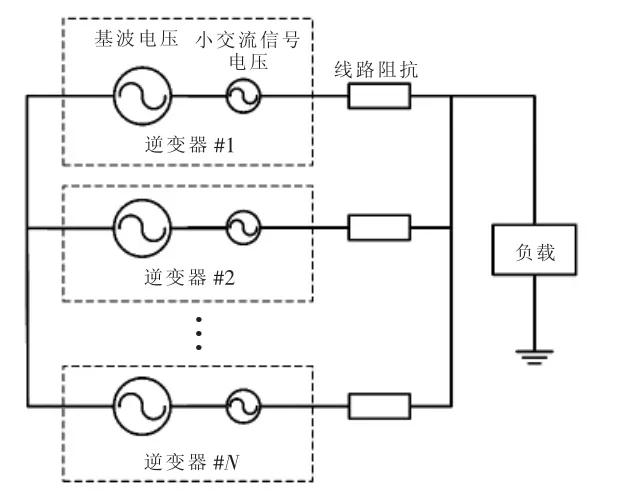
图3 本文方法的N台逆变器并联微网简化示意Fig.3 Simplified schematic of N-parallel-inverter microgrid system using the proposed method

在本文提出的新型二次控制方法中，PCC点的电压幅值和频率都由PI控制器来调节。同时，一个小幅值的交流电压信号被注入系统协助控制。该小交流信号的频率与基波电压的下垂偏置成下垂关系，表示为

式中：和为生成的小交流信号频率指令；p0和q0分别为小交流信号频率p和q的基值； 用以调节频率和电压幅值；和为小交流信号的下垂系数，定义为正。值得注意，当需要对频率和电压幅值同时进行二次调节时，p0和q0的选值不能相同。由于本文仿真和实验中频率和电压幅值是分别调节的，所以p0和q0的选值相同。

小交流信号产生的有功功率加上PI控制器的输出共同生成基波电压的下垂偏置P0和Q0，即

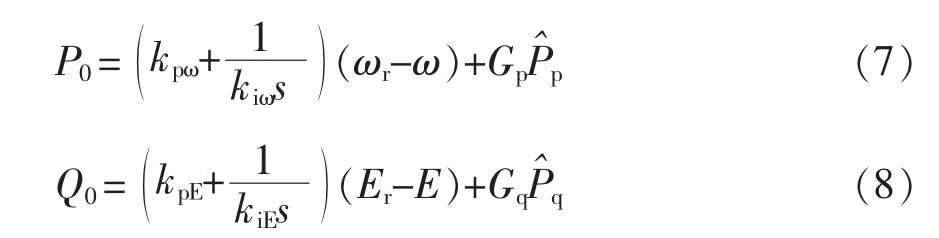
式中：ωr和ω分别为额定频率和实际频率；Er和E分别为 PCC 电压的额定幅值和实际幅值；kpω、kiω和kpE、kiE为调节频率和电压幅值的PI控制器参数；Gp和 Gq为从小交流信号产生的有功功率和到基波电压下垂偏置P0和Q0的增益。小交流信号的电压和电流利用低通滤波器提取，用以计算和。

该二次控制方法的控制框图如图4所示，其中加粗部分代表小交流信号的控制机理，下垂控制的虚线框代表式（3）～式（6），电压指令合成算式为

式中：为注入的小交流信号的电压幅值。

图4 新型二次控制方法的控制框图Fig.4 Control block diagram of a novel secondary control method

在本文提出的新型二次控制方法中，电力传输线被用作并联逆变器之间的通讯线，而注入的小交流信号扮演着通讯信号的角色，其目标在于帮助并联变流器实现功率均分。由式（7）和式（8）可以看出，基波电压的下垂偏置P0和Q0受PI控制器的输出所影响，所以PI控制器能够通过影响P0和Q0从而快速地将PCC点的电压幅值和频率调节至额定值Er和ωr。其次，基波电压的下垂偏置P0和Q0同时受小交流信号产生的有功功率所影响，而P0和Q0与小交流信号的频率呈下垂关系，如式（5）和式（6）所示。因此，该方法实际上是在小交流信号的频率和小交流信号的有功功率之间建立了一种下垂关系。类比传统下垂控制的机理，小交流信号的频率会自我调整，保证稳态时系统中所有并联逆变器输出的小交流信号频率相同，从而式（5）和式（6）可以保证每台逆变器下垂特性中的下垂偏置P0和Q0相同，即稳态时输出的功率相同。因此，通过该二次调节，系统频率和电压幅值不仅可以由PI控制器调节至额定值，而且并联逆变器之间可以实现准确的功率均分。

值得注意的是，如果PI控制器的带宽足够宽，小交流信号产生的有功功率和PI控制器的输出在共同影响P0和Q0时并不会产生冲突。因为当PI控制器带宽较宽时，其能令频率和电压幅值快速跟踪各自的额定值，PI控制器的输出可被看做固定值，此时P0和Q0仅受小交流信号产生的有功功率所影响。

2.2 参数选取

由于在控制注入的小交流信号时需要提取其瞬时电压电流，因此应当避免系统中原有的谐波干扰小交流信号的提取。在选取小交流信号的频率时，应当分析系统中占主要成分的谐波，避免选取主要谐波的频率作为小交流信号的频率。考虑到逆变器输出侧低通滤波器对较高频信号的抑制作用或者对其谐振峰附近频率信号的放大作用，不能选取较高的频率或者低通滤波器谐振峰附近的频率作为小交流信号的频率。另外，当小交流信号的提取算法精度不高时，应当避免将小交流信号的频率选取为基波频率附近或者主要谐波频率附近的频率。当负载为线性负载时，理想PWM调制除了产生基波信号，只会产生开关频率次及其附近以及开关频率整数倍及其附近的谐波，而不会产生低次谐波[18]。然而在工程实际中，由于需要在调制中引入死区，或者为了提高直流电压利用率而利用非正弦波调制，这种情况下系统中会出现低次谐波，其中奇次谐波占主要成分[19]，因此小交流信号的频率不能为基波频率的奇次倍。当负载为非线性负载时，系统中也会出现大量的低次谐波，此时可以选取基波频率非整数倍的频率作为小交流信号的频率且需要利用精度较高的谐波信号提取算法，例如二阶广义积分器 SOGI（second-order generalized integrator）[20]。本文仿真和实验中皆利用线性负载，逆变器输出侧的低通滤波器截止频率为500 Hz，综合上述选取原则，选取基波频率的2倍频或者4倍频较为合适，本文选取基波2倍频，即100 Hz，作为注入小交流信号的频率。

小交流信号的幅值Eˆ的选取应该考察总谐波失真度 THD（total harmonic distortion）的大小，一般电力系统中的THD不能超过5%，而单次谐波的含量不能超过3%[21]。在本文的系统中，基波额定电压幅值为200 V，因此为了给出一定的裕量，注入的小交流信号的幅值设定为3 V，即基波额定电压幅值的1.5%。这样可以实现实验中THD在2%以下。

由于提取并计算得到的小交流信号产生的有功功率和都很小，所以式（7）和式（8）中的系数Gp和 Gq是为了使和的数量级与 P0和 Q0的数量级相当，从而和可以对 P0和 Q0产生足够大的影响。本文的系统中，P0和Q0的数量级为103，而和的数量级为 100～10-1，因此本文中 Gp和Gq的选值数量级为几千。

3 仿真结果

利用仿真软件PSCAD/EMTDC验证了所提出新型二次控制方法有效性。仿真系统由2台三相逆变器并联组成，每台逆变器主电路和控制机制如图4所示。仿真的关键控制参数如表1所示。

第1组仿真验证新型二次控制方法对频率和有功功率的调节作用。在t=2 s时，有功负载增加8 kW，频率随之由49.96 Hz降低至49.58 Hz。t=5 s时手动开启二次控制（所提出的新型二次控制应是连续调节的，在本文的仿真和实验中，二次控制均由手动触发，是为了更清晰地演示调节过程）。图5所示为文献[16]中的分布式二次控制的调节过程，可以看到虽然频率恢复至额定值50 Hz，但是无法实现有功功率在并联逆变器之间的均分。本文提出的二次控制方法仿真过程波形如图6所示。由图可见，不仅可以实现频率恢复，同时可以实现有功功率的均分。

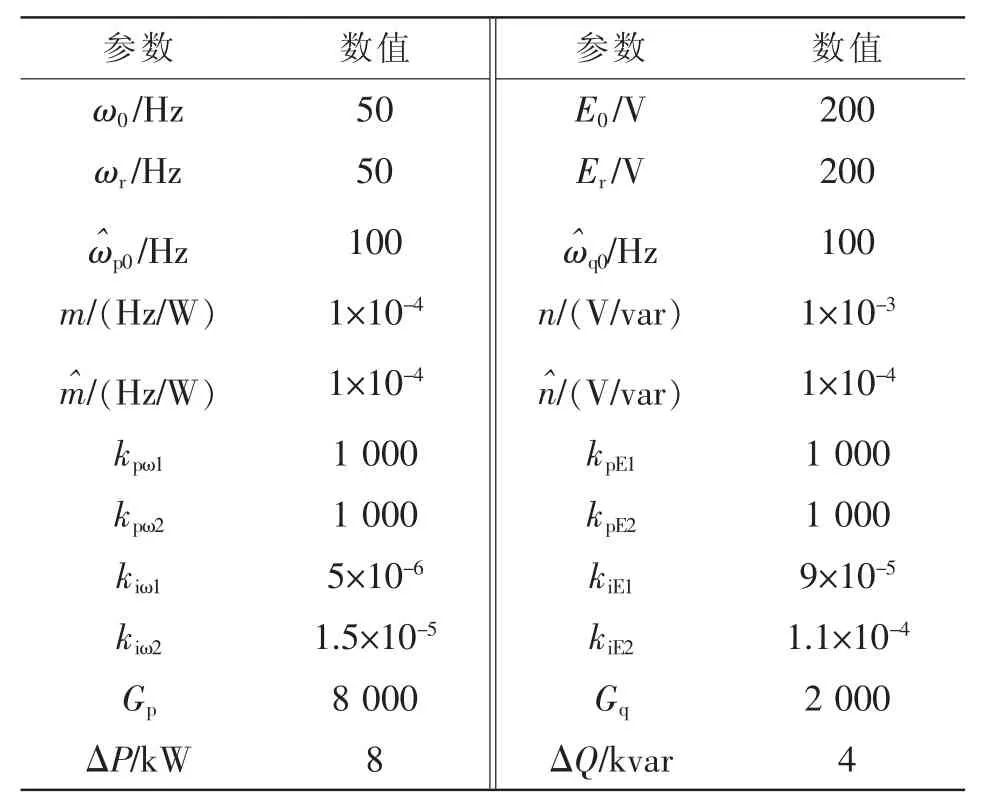
表1 仿真参数Tab.1 Simulation parameters

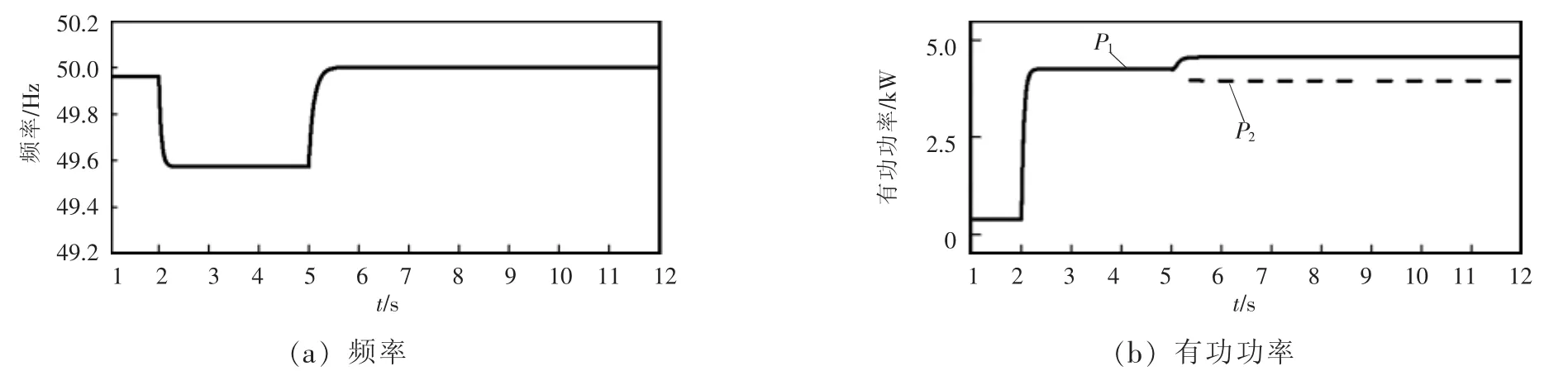
图5 传统分布式二次控制下频率和有功功率的仿真波形Fig.5 Simulation waveforms of frequency and active power using the traditional distributed secondary control method

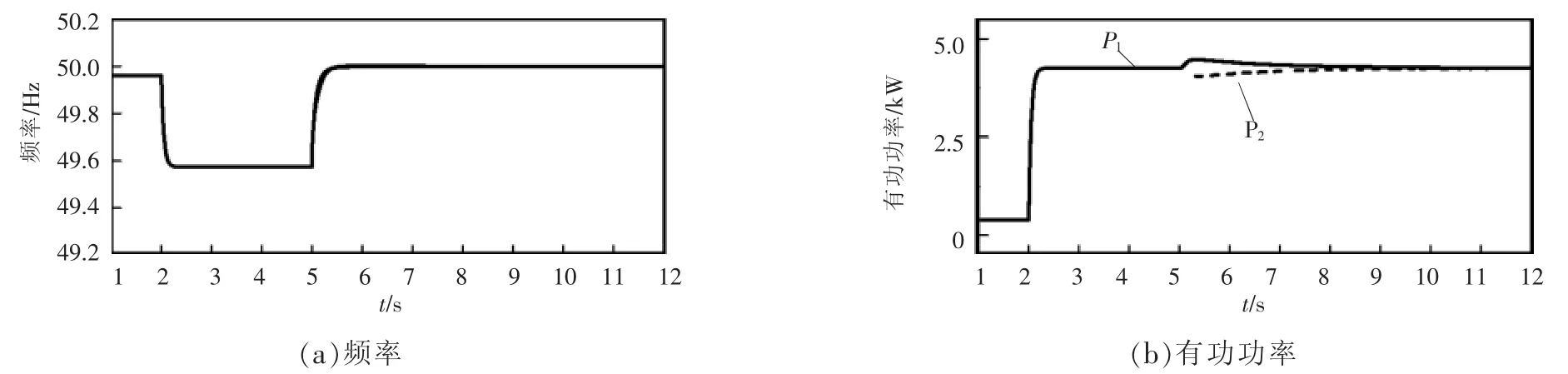
图6 新型二次控制下频率和有功功率的仿真波形Fig.6 Simulation waveforms of frequency and active power using the proposed secondary control method

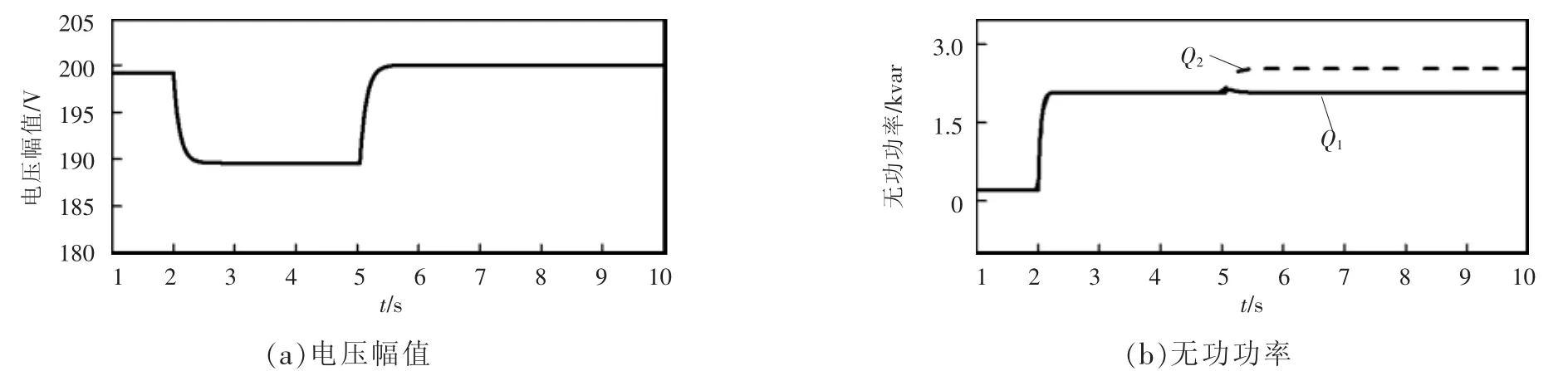
图7 传统分布式二次控制下电压幅值和无功功率的仿真波形Fig.7 Simulation waveforms of voltage amplitude and reactive power using the traditional distributed secondary control method

第2组仿真验证新型二次控制方法对电压幅值和无功功率的调节作用。在t=2 s时，无功负载增加4 kvar，电压幅值随之由199.2 V降低至189.6 V。t=5 s时手动开启二次控制。图7所示为文献[16]中的分布式二次控制的调节过程，可以看到虽然电压幅值恢复至额定值200 V，但是无法实现无功功率在并联逆变器之间的均分。本文提出的二次控制方法仿真过程波形如图8所示。由图可见，不仅可以恢复电压幅值，同时可以实现无功功率的均分。

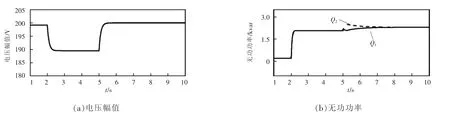
图8 新型二次控制下电压幅值和无功功率的仿真波形Fig.8 Simulation waveforms of voltage amplitude and reactive power using the proposed secondary control method

4 实验验证

通过硬件实验验证所提出新型二次控制方法的有效性。实验平台由2台相同规格的三相逆变器并联组成，每台逆变器的控制机制如图4所示，实验参数如表2所示。频率、电压幅值和输出功率的波形是在Origin软件中根据功率分析仪HIOKI Power Analyzer 3390采集的数据画出。

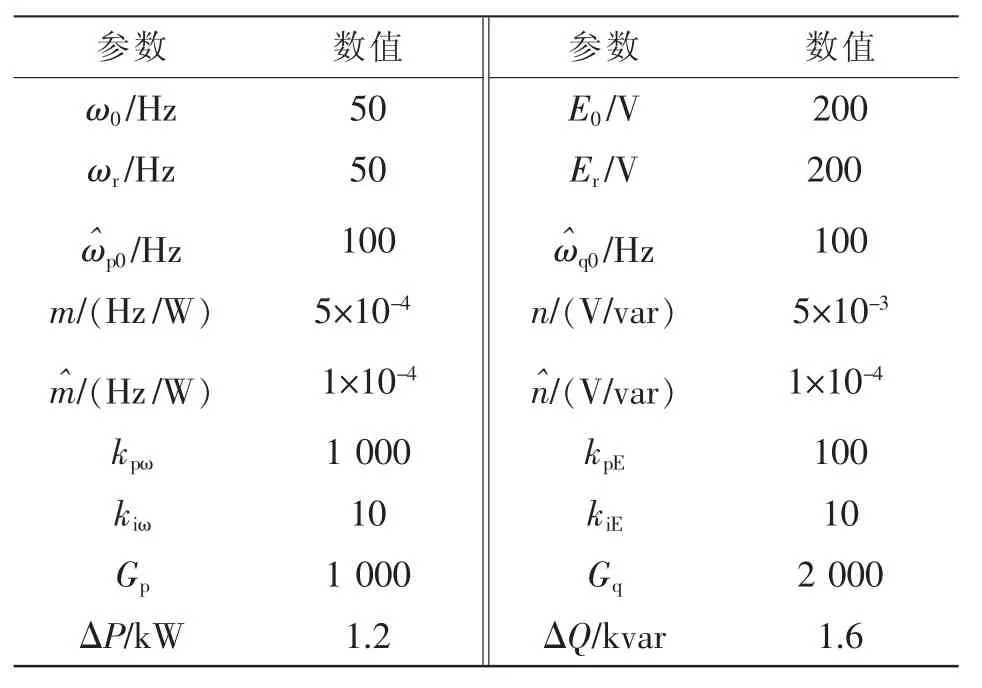
表2 实验参数Tab.2 Experimental parameters

第1组实验验证了提出的新型二次控制方法对频率和有功功率的调节作用。图9所示为频率和有功功率的实验波形。开始时刻，2台逆变器都是下垂控制，在t=17 s时，有功负载增加1.2 kW，频率随之由49.76 Hz降低至49.47 Hz。t=33 s时开启二次控制。由图可以看到，频率随之恢复至49.99 Hz且2台逆变器输出的有功功率均分。

第2组实验验证了提出的新型二次控制方法对电压幅值和无功功率的调节作用。图10所示为电压幅值和无功功率的实验波形。开始时刻，2台逆变器都是下垂控制，在t=17 s时，无功负载增加1.6 kvar，电压幅值随之由199.4 V降低至195.5 V。t=35 s时开启二次控制。由图可以看到，电压幅值随之恢复至200.5 V，且2台逆变器输出的无功功率均分。

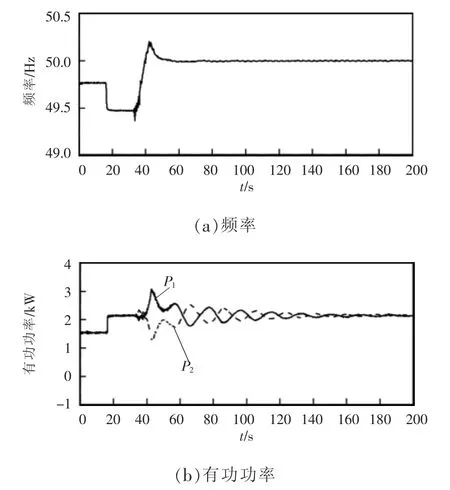
图9 新型二次控制的实验波形Fig.9 Experimental waveforms of the system frequency and the output real power

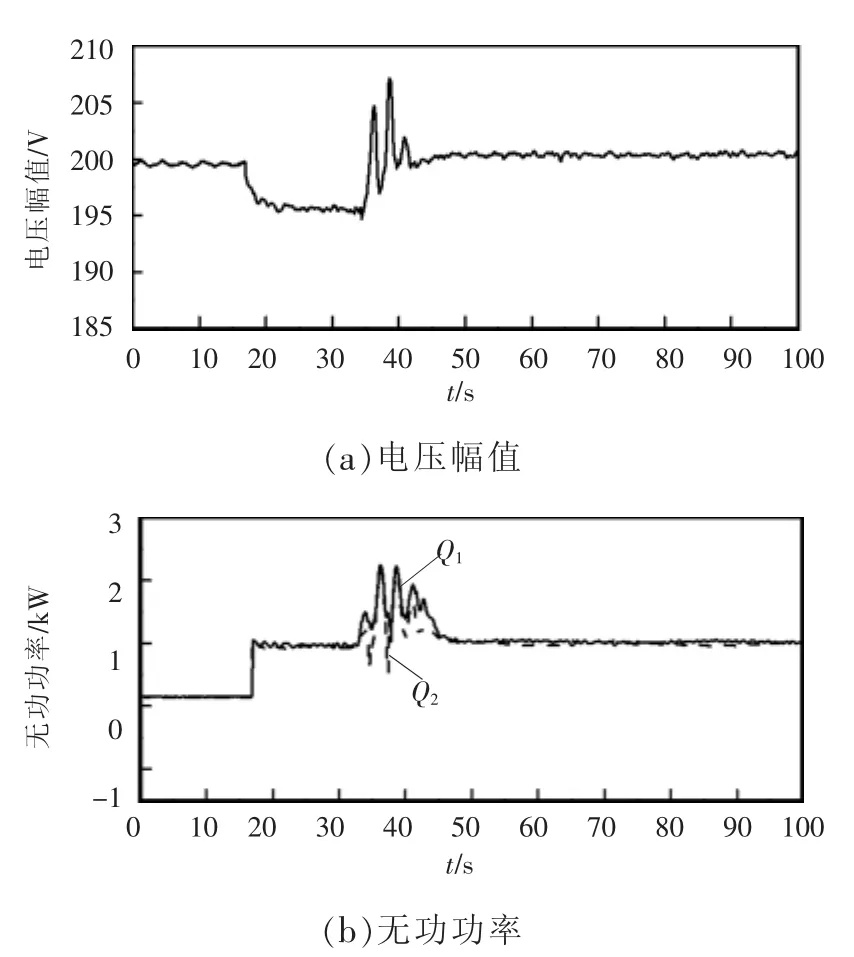
图10 新型二次控制的实验波形Fig.10 Experimental waveforms of the voltage amplitude and the output reactive power

5 结语

本文提出了一种基于小交流信号的微网新型二次控制方法。该方法首先通过PI控制器调节PCC点的电压幅值和频率，其次通过控制注入的小交流信号的频率来同步调整逆变器输出基波电压的下垂偏置，从而保证并联逆变器的稳态工作点相同，实现负载功率在并联逆变器之间的平均分配。因此，该方法不仅可以调节频率和电压幅值至额定值，还可以在无互联线的情况下实现并联逆变器之间的功率均分。最后，本文通过仿真和实验验证了所提出二次控制方法的有效性。

[1]Piagi P,Lasseter R H.Autonomous control of microgrids[C].Proceedings of the Power Engineering Society General Meeting,Montreal,Canada,2006:1-8.

[2]Rocabert J,Luna A,Blaabjerg F,et al.Control of power converters in AC microgrids[J].IEEE Transactions on Industrial Electronics,2012,27（11）:4734-4749.

[3]Chandrasena R P S,Shahnia F,Rajakaruna S,et al.Control,operation and power sharing among parallel converter-interfaced DERs in a microgrid in the presence of unbalanced and harmonic loads[C]//Proceedings of the Australasian U-niversities Power Engineering Conference.Hobart,Australia,2013:1-6.

[4]Lasseter R H.MicroGrids[C].Proceedings of the Power Engineering Society Winter Meeting,2002:305-308.

[5]Lasseter R H.Smart distribution:coupled microgrids[J].Proceedings of the IEEE,2011,99（6）:1074-1082.

[6]Guerrero J M,Chandorkar M,Lee T,et al.Advanced control architectures for intelligent microgrids-Part I:decentralized and hierarchical control[J].IEEE Transactions on Industrial Electronics,2013,60（4）:1254-1262.

[7]Kroposki B,Pink C,DeBlasio R,et al.Benefits of power electronic interfaces for distributed energy systems[J].IEEE Transactions on Energy Conversion,2010,25（3）:901-908.

[8]Khalil A,Alfaitori K A,Elbarsha A.Stability analysis of parallel-inverters in microgrid[C]//Proceedings of the 20th International Conference on Automation and Computing.Bedfordshire,UK,2014:110-115.

[9]Guerrero J M,Hang L,Uceda J.Control of distributed uninterruptible power supply systems[J].IEEE Transactions on Industrial Electronics,2008,55（8）:2845-2859.

[10]Guerrero J M,Vasquez J C,Matas J,et al.Control strategy for flexible microgrid based on parallel line-interactive UPS systems[J].IEEE Transactions on Industrial Electronics,2009,56（3）:726-736.

[11]Hu Jiefeng,Zhu Jianguo,Dorrell D J,et al.Virtual flux droop method—a new control strategy of inverters in microgrids[J].IEEE Transactions on Power Electronics,2014,29（9）:4704-4711.

[12]Hua Ming,Hu Haibing,Xing Yan,et al.Multilayer control for inverters in parallel operation without intercommunications[J].IEEE Transactions on Power Electronics,2012,27（8）:3651-3663.

[13]Wu Teng,Liu Jinjun,Liu Zeng,et al.Load power estimation based secondary control for microgrids[C].Proceedings of the 9th International Conference on Power Electronics（ICPE-ECCE Asia）,Seoul,Korea,2015:722-727.

[14]张轩,刘进军.微网孤岛运行时基于逆变器的新型功率控制[J].电源学报,2011,9（1）:38-42.Zhang Xuan,Liu Jinjun.A novel power distribution strate-gy for parallel inverters in islanded mode microgrid[J].Journal of Power Supply,2011,9（1）:38-42（in Chinese）.

[15]Guerrero J M,Vasquez J C,Matas J,et al.Hierarchical control of droop-controlled AC and DC microgrids-a general approach toward standardization[J].IEEE Transactions on Industrial Electronics,2011,58（1）:158-172.

[16]Shafiee Q,Guerrero J M,Vasquez J C.Distributed secondary control for islanded microgrids-a novel approach[J].IEEE Transactions on Power Electronics,2014,29 （2）:1018-1031.

[17]Tuladhar A,Jin Hua,Unger T,et al.Control of parallel inverters in distributed AC power systems with consideration of line impedance effect[J].IEEE Transactions on Industrial Applications,2000,36（1）:131-138.

[18]Hamman J,Van Der Merwe F S.Voltage harmonics generated by voltage-fed inverters using PWM natural sampling[J].IEEE Transactions on Power Electronics,1988,3（3）:297-302.

[19]Evans P D,Close P R.Harmonic distortion in PWM inverter output waveforms[J].IEEE Transactions on,2000,36（1）:131-138.

[20]He J,Li Y,Blaabjerg F.An enhanced islanding microgrid reactive power,imbalance power,and harmonic power sharing scheme[J].IEEE Transactions on Power Electronics,2015,30（6）:3389-3401.

[21]IEEE Power and Energy Society.IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems:IEEE Std 519-2014[S].New York:The Institute of Electrical and Electronics Engineers,2014.