一种应用于双锥型液-液旋流器的导叶设计新方法

何利民，田洋阳，罗小明

(中国石油大学 储运与建筑工程学院，山东 青岛 266580)

导叶式轴流液-液旋流器具有径向尺寸小、结构紧凑、压力损失小、改善入口处循环流、分离效率高且流场更加稳定的优点[1]，在处理空间有限的石油生产现场中具有广泛的应用前景。与切向式液-液旋流器不同，轴流式液-液旋流器是利用导叶结构对流体产生导向作用，重相在离心力的作用下往器壁方向运动，轻相则相反，从而完成密度不同的两相的分离。

作为分离器的关键部件，导叶的设计也就成了液-液旋流器研究的重点问题。液-液旋流器的导叶结构不仅要使流体转向，而且要保证分离。据笔者调研发现，导叶的设计方法主要分为几何设计法和气动设计法，国内研究者多采用几何设计法，国外研究者多采用气动设计法借鉴空气动力学翼型展开研究。

采用几何设计法的观点认为，叶片型线是由2条曲线组成的，通常1条二次曲线如圆弧线、抛物线等与1条直线段相连。毛羽等[2]和张荣克等[3]利用1根母线和1个圆柱面相交成一定角度，沿圆柱面某种曲线移动而形成的曲面设计了导叶，应用于旋风分离器中；金有海等[4]对旋风管叶片参数进行了实验研究，确定了叶片出口角的设计原则，建立了圆弧正交叶片的型线方程。由于叶型曲率极大地决定着沿叶片表面的速度分布和压力分布，这种方法由于在叶片成型过程中未考虑到曲率的连续性，在圆弧段与直线段相接处易产生曲率的突变，从而导致叶片表面速度和压力的突变，针对液-液旋流器很可能出现局部剪切力过高，从而导致液滴的破碎，影响分离效率。

有关气动设计法的代表性研究有：1996年Dirkzwager[5]首次成功设计了安装有旋流元件的液-液轴流旋流器，这种旋流元件是利用空气动力学的标准翼型而设计，研究表明，这种新型的旋流器结构更加紧凑且压力降更低，应用范围很广。随后，van Campen等[6-7]和Slot[8]也利用NACA四位数翼型建立了轴流旋流器的旋流元件，获得了良好的分离效果。上述这些导叶的设计方法虽然是采用气动法，但均是通过弯曲原始叶型的中弧线进行设计的，该方法只需要确定中弧线方程和叶片厚度方程即可，该方法的弊端是，方程内各个参数的含义不明确，进一步优化调整叶型时存在盲目性，工作量较大。

据笔者调研发现，关于导叶设计的研究，大都针对涡轮和压缩机叶片，而针对液-液旋流器叶片的研究较少，同时也缺少系统的、可实际操作的导叶设计流程。涡轮和压气机导叶包含静子和转子，并且多级运转，还要考虑到气体的可压缩性影响，因此比液-液旋流器叶片更为复杂，但这两种叶片存在共性，均可实现使流体加速并转向。故借鉴经验丰富的涡轮和压气机叶片设计方法，提出一种新的适用于液-液旋流器的导叶设计方法，在气动设计法的基础上，采用直接根据叶型各个几何参数绘制型线，其中导叶设计的流程(如图1所示)主要分为初始导叶设计和优化导叶两大部分。笔者主要针对初始导叶设计展开研究，详细叙述了具体的设计步骤及参数的取值，为工业应用提供了可行的参考。

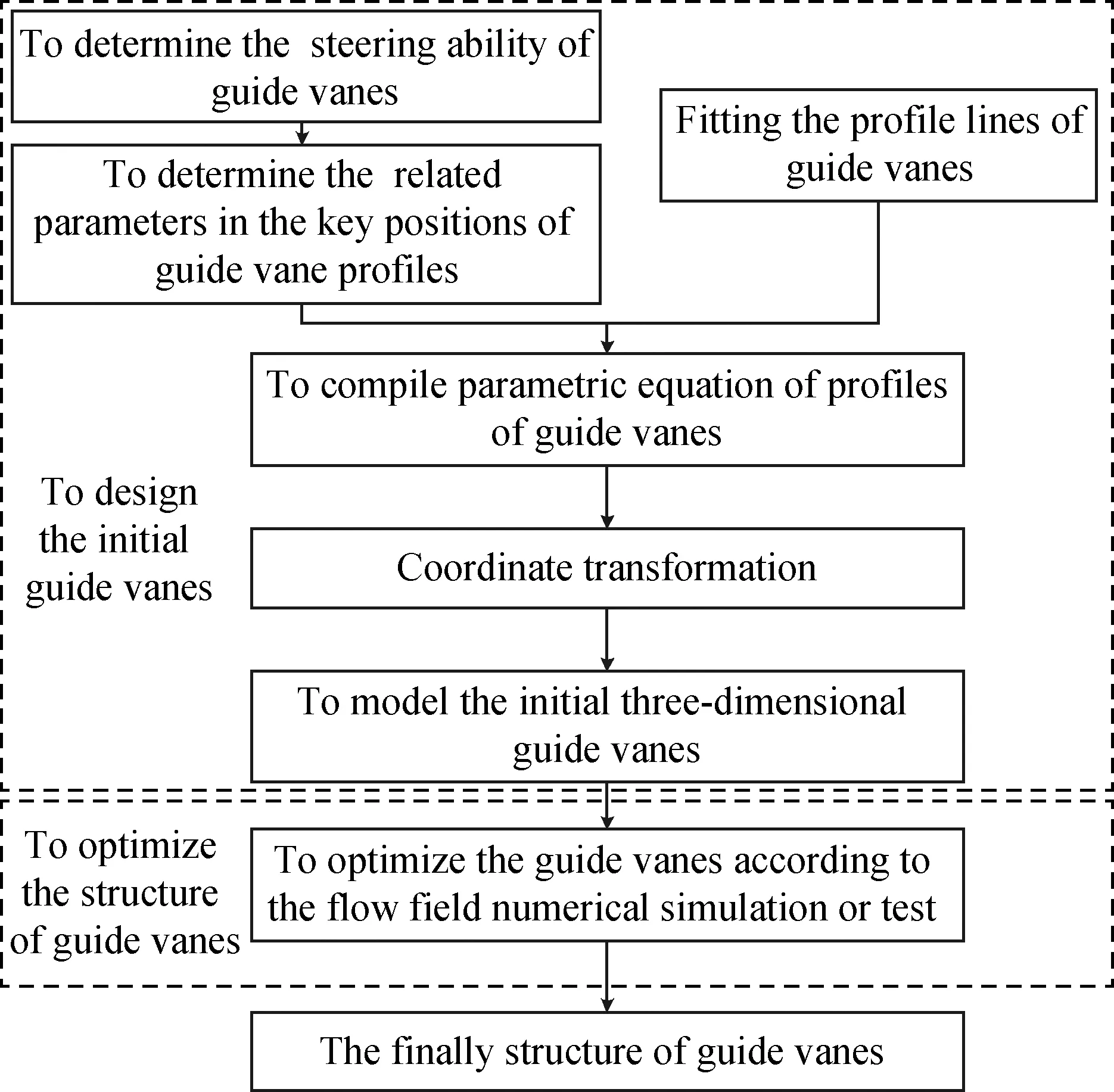
图1 导叶设计流程Fig.1 The process of the guide vanes design

1 导叶对液流的转向能力设计

对于初始导叶设计，首先要确定的就是导叶对液流的转向能力，即液流出口角β2。考虑最理想的情况，流体从轴向进入导叶(液流入口角β1为90°)，在导叶的约束下加速转向，通过分析指定直径油滴运动到油芯位置(假设认为油滴被分离)所需的切向速度和轴向速度，可计算出液流出口角β2，具体的分析方法如下。

1.1 油滴径向速度估算

油滴在旋流器内迅速朝管中心迁移，在径向方向上受到阻力和离心力的作用，达到受力平衡后，可以得到油滴的径向速度：

(1)

式中：vr为油滴的径向速度，m/s；Δρ为油水的密度差，kg/m3；d为油滴直径，m；vu为油滴的切向速度，m/s；rp为油滴所处的径向位置，m；μwater为水的黏度，Pa·s。

1.2 油滴切向速度估算

根据文献[5,7,9]可知，双锥旋流器中的切向速度分布呈现兰金涡(Rankin)，即中心处为强制涡，外侧为准自由涡。这样的速度分布可采用下式计算：

(2)

式中：r为旋流器的径向位置变量，m；z为旋流器的轴向方向变量，m；Uu为切向速度数量级量值，m/s；Rcyclone为旋流器半径，m；Rc为强制涡旋转中心半径，m。

根据Dirkzwager[5]的实验数据，Rc/Rcyclone≈0.25。Uu(z)依赖于流体流动过程中轴向的旋流衰减模型，可以表示为：Uu(z)=Uu(0)e-Cdecayz/2Rcyclone，根据Dirkzwager[5]的实验数据，旋流衰减系数Cdecay为0.04。

为了获得Uu(z)的具体表达式，进行了以下推导。首先，从径向速度的定义出发，得到径向速度与轴向速度关系式：

(3)

式中：τ为时间，s；vz,averge为轴向的平均速度，m/s。

其次，结合式(1)和式(2)，可得液滴径向位置沿轴向的分布rp(z)：

(4)

当油滴进入导叶时(z=0)，位于旋流器外径的最大处，最不利于分离，故令rp(0)=Rcyclone。

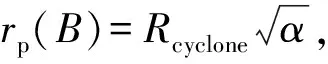
最后，结合rp(B)和rp(0)，得到Uu(z)的表达式如下：

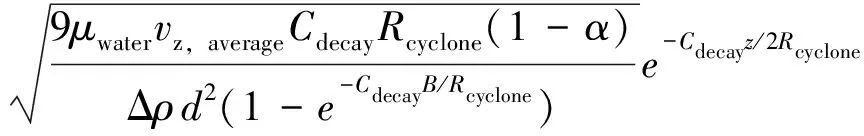
(5)

1.3 液流出口角β2估算

液流出口角β2为导叶出口处的切向速度与轴向速度的夹角，即：

(6)

旋流器的导叶内径为Rin，导叶外径等于旋流器半径Rcyclone。故根据质量守恒可得到导叶出口处的轴向速度vz,2：

(7)

导叶出口处的切向速度vu,2可通过角动量守恒定理式得到：

(8)

根据Dirkzwager[5]测得大约50%的角动量在导叶部位损失了，即导叶部位角动量损失系数εloss为0.5，故式(8)可化简为：

(9)

2 叶型关键位置的相关参数设计

初始叶片设计时，首先确定以下关键参数：叶型的几何进口角β1r、几何出口角β2r、安装角γ、轴向弦长B、入口尖角ω1、出口尖角ω2、入口小圆直径φ1、出口小圆直径φ2、喉部宽度η、叶栅间距tys以及后缘转折角δ。初始叶型的这些关键参数的确定方法，在很多涡轮叶片的文献中均有报道，考虑到液-液旋流器内导叶的流动特点，笔者筛选出了适用于不可压缩流体、低速流动条件下的关键参数的经验公式和推荐取值范围，这些经验公式和推荐取值范围是根据大量的平面叶栅试验数据统计曲线或经验公式计算得出的，并已经通过试验验证。试验表明，在马赫数Ma小于0.5，雷诺数Re大于(2.5～3.0)×105的流动范围内，气体的压缩性和黏性都可忽略[10]，下面具体介绍各个参数的确定方法。

几何入口角β1r可采用文献[10]中的经验公式进行估算，具体形式如下：

(10)

式中：β1为液流入口角，°；β2为液流出口角，°。

几何出口角β2r可采用文献[11]提供的公式(11)近似计算，其中修正角Δβ的取值可参阅文献[11]中的图4.11。

(11)

安装角γ推荐采用文献[11]中的经验公式，具体形式如下：

(12)

入口尖角ω1和出口尖角ω2是与叶型最大厚度及最大厚度所在位置有关的量，根据文献[10]，通常推荐入口尖角ω1在10°～38°范围内，出口尖角ω2在1°～4°范围内。

入口小圆直径φ1推荐比出口小圆直径φ2大些，推荐取值范围在0.008倍到0.081倍弦长l之间[11]。为了减小尾迹损失，出口小圆直径φ2应尽量选小些，推荐取值范围在0.01倍到0.05倍弦长l之间[11]。

在初始叶型中除了保证流体的转向之外，还应使流体加速，故旋流器的导叶流道是收缩的，收缩程度与喉部宽度η有关，推荐采用公式：

η=tyscos(90-β2r)-φ2

(13)

叶栅间距tys推荐取值范围1.8倍到2.0倍弦长l之间[10]。

后缘转折角δ推荐在8°～10°范围内，不大于15°[10]。

3 导叶参数化建模

导叶的参数化建模是通过导叶的主要参数建立导叶的结构模型，其优势在于通过改变模型中的参数值就能够轻松地建立新的导叶结构模型，便于设计优化导叶的结构。确定了叶型关键位置的相关参数后，需要用一条或几条曲线将这些关键位置连接起来，从而形成导叶的型线。通过文献调研可知，研究者们常采用B样条曲线[12]、非均匀样条(NURBS)曲线[13-14]、多项式曲线[15]和贝赛尔(Bezier)曲线[16-18]描述涡轮叶片的型线，是否具有良好的形状控制能力是判断这些方法优劣的其中标准之一[19]。由于Bezier曲线的切矢性对实现叶型角控制非常方便，并且三次Bezier曲线由4个控制点组成，其控制参数少，便于编程实现，故笔者采用Bezier曲线进行导叶的参数化建模。

3.1 Bezier曲线简介

一条Bezier曲线由一些空间点构成的控制多边形确定。n阶Bezier曲线由n+1个控制点确定，其矢量表达式为：

(14)

式中，Bj,n(t)为Bernstein函数，Pj为n+1个空间控制点矢量；P(t)为Bezier曲线矢量;t为叶型参数方程中的参数，t∈[0,1]。

3.2 2条Bezier曲线的曲率连续

单一的Bezier曲线不能满足复杂形状的需要时，需采用组合Bezier曲线，以满足实际需要，同时提出了新的问题——2条曲线光滑连接的问题。根据文献[20]经验，叶型的后弯角和叶背曲率，特别是背弧斜切部分的曲率对导叶性能影响十分重要，因此为了更准确地控制叶背曲线，采用2条保证曲率连续的二次Bezier曲线方程描述叶背型线。

导叶的各关键点的位置如图2所示，叶背型线的5个控制点分别为g、a、p、b、f，构造2条Bezier曲线，其曲线方程如下：

(15)

为了保证曲线gap和pbf在公共点p处达到曲率连续，则需满足以下条件[21]：

根据式(15)及以上连续条件推导得到：

(16)

故为了满足曲率连续条件，a点和b点坐标由式(16)推导得到：

(17)

3.3 导叶型线的拟合

图2为导叶型线拟合关键点位置图，将坐标原点O定义在弦线与出口额线交点处。前、后缘圆弧与压力边和吸力边相切点c、g、q、f的切线的夹角为入口出口尖角。c、q为压力边三次Bezier曲线的特征多边形的始、终顶点。吸力边由2段二次Bezier曲线组成，g、p为第1段二次Bezier曲线的特征多边形的始、终顶点，p、f为第2段二次Bezier曲线的特征多边形的始、终顶点。

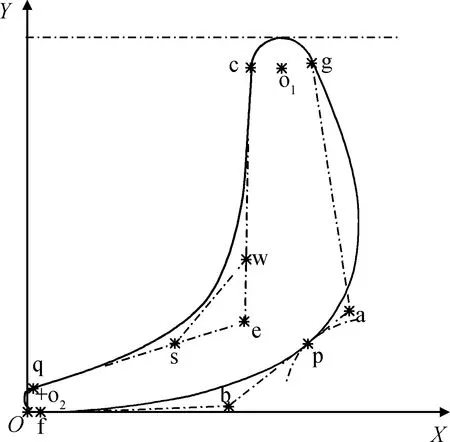
图2 导叶型线拟合关键点位置图Fig.2 Positions of key fitting points of guide vane profiles

压力边与后缘圆弧切点q坐标为：

(18)

吸力边与后缘圆弧切点f坐标为：

(19)

压力边与前缘圆弧切点c坐标为：

(20)

吸力边与前缘圆弧切点g坐标为：

(21)

e为压力边前后缘切线的交点，则切线qe的斜率Kqe为：

(22)

切线ce的斜率Kce为：

(23)

点e的坐标为：

(24)

s、w分别为qe、ce上的点，为了实现s、w位置的参数化表示，定义了2个分别与s、w相关的表示分割线段的比例的参数h和h*，其值在0到1的范围内。

点s的坐标为：

(25)

点w的坐标为：

(26)

喉部点p的坐标为：

(27)

吸力边前后缘切线与喉部切线的交点分别为a、b，这两点的坐标为满足曲率连续条件的式(17)。

根据点q、s、w、c的坐标，得到压力边的三次Bezier曲线表达式：

(28)

根据点g、a、p、b、f的坐标，得到2条吸力边的二次Bezier曲线表达式：

(29)

(30)

综上所述，建立了导叶型线的参数化表达式(28)～(30)，型线的形状由以下全部13个设计参数唯一确定：几何进口角β1r、几何出口角β2r、安装角γ、轴向弦长B、入口尖角ω1、出口尖角ω2、入口小圆直径φ1、出口小圆半径φ2、喉部宽度η、叶栅距离tys、后缘转折角δ，形状控制参数h、h*。

3.4 编制叶型参数化方程及三维造型

利用Matlab编制了导叶型线的参数化表达式的程序，借助该程序只需输入初始叶型的相关参数(参照本文第2小节的参数确定方法)，就可获得导叶型线的参数化表达式，以及吸力边、压力边、前缘圆弧和后缘圆弧坐标值和叶型曲线图。三维实体模型可通过输出的坐标值，经坐标转换，在Solidworks中通过“插入曲线”，“放样曲面”、“填充曲面”、“阵列”等操作获得。

4 导叶设计造型实例及性能验证

4.1 导叶设计造型实例

液-液旋流器的设计参数：外径50 mm，内径40 mm，入口流速2 m/s，+20#柴油密度870 kg/m3，水密度996 kg/m3，油体积分数为10%，通过本文第2小节所述设计计算出导叶结构参数，结果如表1 所示。通过Matlab和Solidworks建立的导叶截面叶型和三维模型分别如图3和图4所示。

表1 导叶结构参数Table 1 Parameters of guide vanes

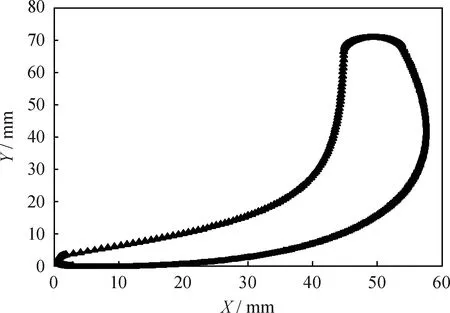
图3 导叶截面叶型图Fig.3 Diagram of vane profiles of guide vane section

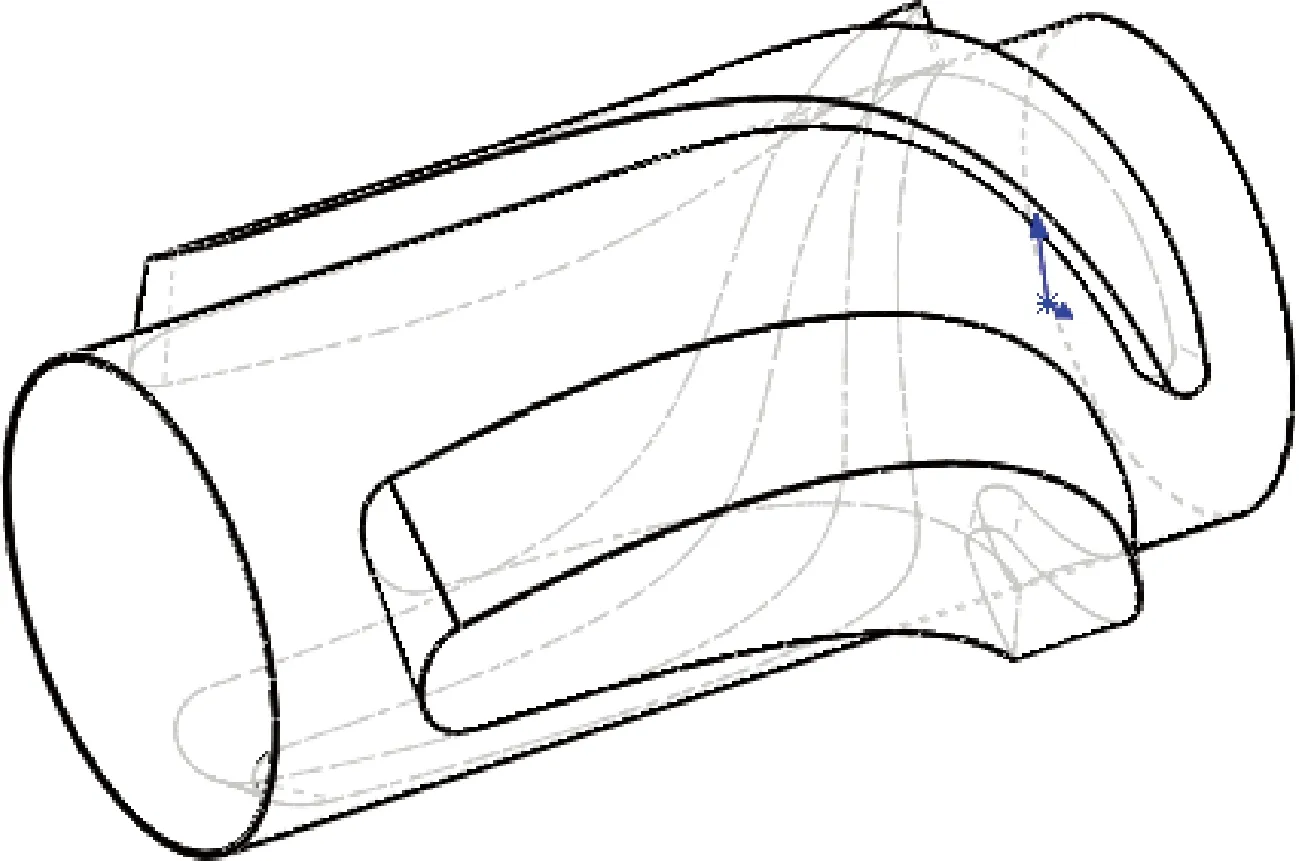
图4 导叶三维模型图Fig.4 Three-dimensional model diagram of guide vanes

4.2 导叶实例的性能验证

为了验证新方法设计出的导叶性能优劣，针对新方法导叶结构与相同设计参数的几何法导叶结构进行对比研究，其中几何法导叶由最常用的圆弧和直线相接叶片组成[4]。为了确保2种设计方法的导叶结构的可比性，2种导叶结构采用相同的设计参数，其中几何出口角β2r为16.6°，导叶个数N为3，导叶轴向弦长B为0.071 m，导叶包弧长S为0.056 m，其结构如图5所示。

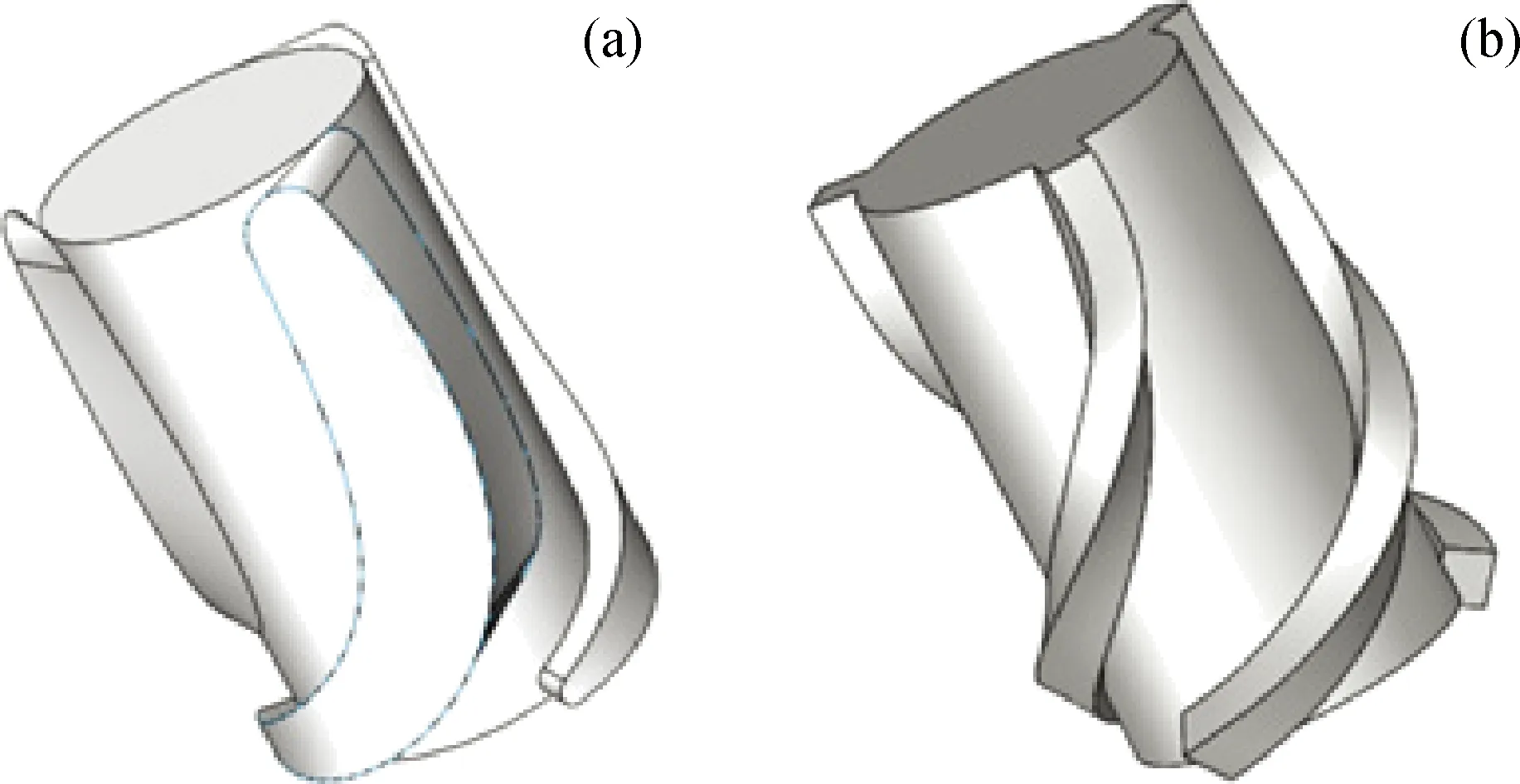
图5 2种设计方法的导叶结构图Fig.5 Diagram of guide vane structure designed with two design methods(a) Guide vanes designed by the new method；(b) Guide vanes designed by the geometric method

4.2.1 导叶型线的曲率连续性及光滑性分析

曲率是表示平面曲线弯曲程度的重要参数，型线曲率将直接影响叶面的势函数分布，进而影响当地的速度和压力值。不光滑的曲率将引起压力和速度分布不光滑，导致流动在某些局部区域上出现小的扩压和分离，从而影响旋流器的分离效果。叶型型线的曲率k根据式(31)计算，并通过Matlab计算2种导叶型线的曲率，曲率半径分布如图6所示。

(31)

从图6可知，新方法导叶的曲率半径连续，而相同叶片参数下的几何法导叶的曲率半径在圆弧段和直线段连接处出现了明显跳跃，并且这种曲率不连续是由于直线和圆弧的特性决定，不可消除，故在跳跃点附近会出现压力和速度的突变，易产生流动的扩压和分离，不利于实现分离。

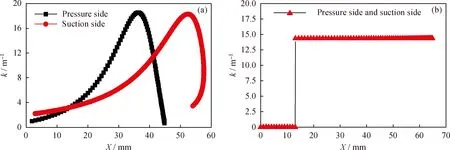
图6 2种导叶型线的曲率半径随导叶X轴位置参数的变化Fig.6 Variations of curvature radii with X axis location of two guide vane profiles(a) Guide vanes designed with the new method；(b) Guide vanes designed with the geometric method

叶型型线的光滑性检查是通过叶型坐标的二次差变化曲线来研究[10]，二次差根据式(32)计算，并通过Matlab检查2种导叶型线的光滑性，结果如图7 所示。

Δsi=Δoi+1-Δoi=[y(i+2)-y(i+1)]-
[y(i+1)-y(i)]

(32)

由图7可知，新方法导叶的光滑性质量高，而相同叶片参数下的几何法导叶在圆弧段和直线段连接处也出现了不连续的问题，导致连接处发生速度和压力的突变，易产生二次涡，造成不必要的能量损失，同时也会使局部剪切力过高，令液滴破碎，影响分离效率。

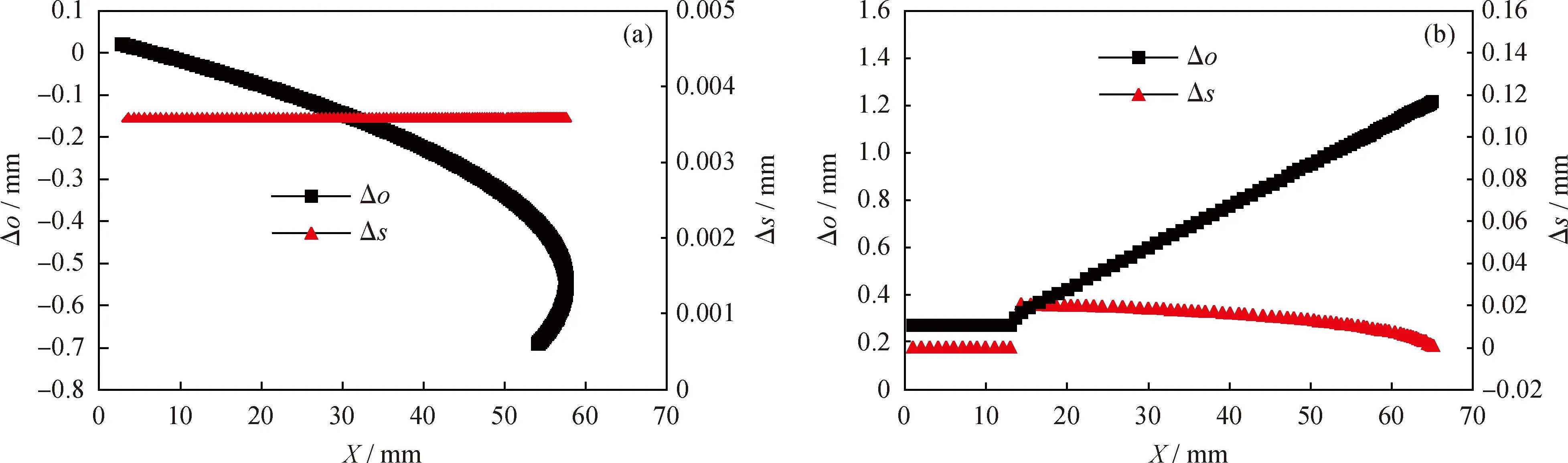
图7 2种导叶型型线光滑性检查Fig.7 Examination of smoothnesses of two guide vane profiles(a) Guide vanes designed with the new method；(b) Guide vanes designed with the geometric method

4.2.2 导叶型线的控制性

几何法导叶的叶型准线方程详见文献[4]，方程中叶型参数只有4个：几何出口角β2r，导叶个数N，导叶轴向弦长B，导叶包弧长S。由于控制参数较少，因此对叶型的控制性较弱，特别是需要反复调整的关键位置如叶背斜切部分无法直接调节。此外，根据现有文献[2-4]资料，叶片包弧长S没有明确的参考范围或者经验公式，并且根据准线对叶片的造型方法也未有参考或推荐，都是依靠设计者的经验而定，不利于进一步改善导叶的性能。

新方法导叶型线的形状由13个设计参数确定，且每个设计参数都有明确的参考范围或经验公式，通过调整任意参数的值就可以得到不同叶型，如图8 所示。由图8可知，新方法导叶的13个设计参数对叶型的描述更加充分，即具有良好的形状控制能力。此外，每个设计参数的含义也更加明确，便于有针对性地快速修改设计参数并再生模型。针对不同优化要求，新方法可以实现形象化的、精确的调节。因此，对于缺乏经验的设计者也可以快速理解和准确调整导叶结构，可供工程应用。

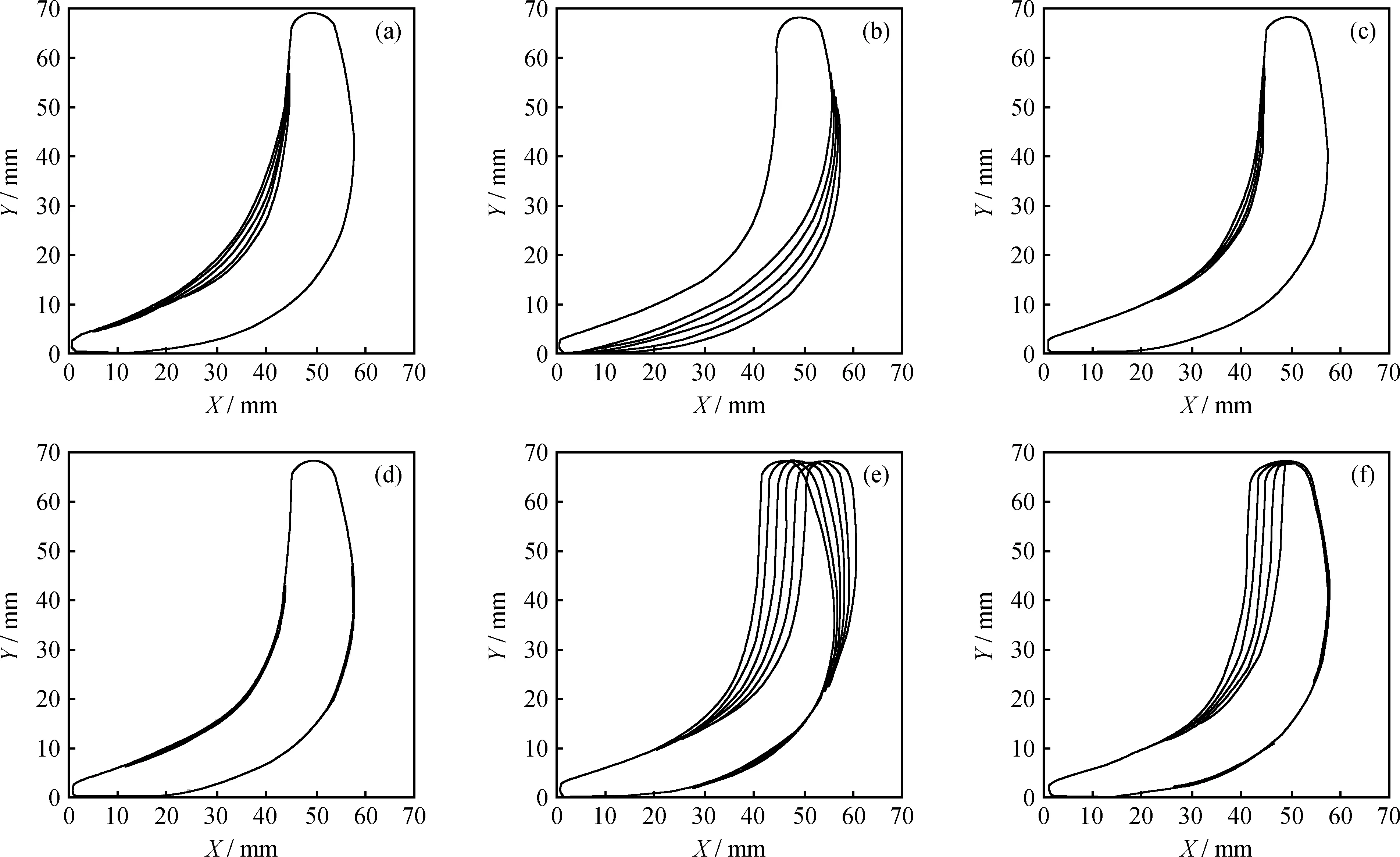
图8 导叶型线随设计参数值的变化Fig.8 Variation diagrams of guide vane profiles with parameter change(a) Change the value of h；(b) Change the value of η；(c) Change the value of β1r；(d) Change the value of ω2；(e) Change the value of γ；(f) Change the value of φ1

4.2.3 导叶的流场特性

采用Fluent软件对2种导叶的双锥型液-液旋流器进行数值模拟，分析其流场特性。由于导叶结构存在大角度弯曲的曲线，采用非结构化网格，其余部分采用结构化网格。模拟采用瞬态进行，速度压力场采用SIMPLE算法，边界层处理采用标准壁面函数；计算介质为水，其密度为996 kg/m3，黏度为0.001003 kg/(m·s)；入口边界采用速度入口，入口速度为2 m/s；底流口及溢流口出口边界均采用自由出流；壁面为无滑移边界条件。

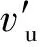
静压分布特性是导叶产生的流场的特性之一，对旋流器有着重要的影响，因此展开了相关研究。为方便对比观察，将纵坐标静压用新方法的最大静压值进行归一化处理，用符号p′表示；将横坐标径向位置用旋流器的最大半径进行归一化处理，用符号ψ表示。结果如图9(c)、(d)所示，其中(c)中曲线为导叶段和大椎段位置的静压分布，(d)中曲线为小锥段位置的静压分布。静压在2种导叶产生的流场中的分布规律和数值都很相似，沿径向从器壁向轴心逐渐降低，在器壁上压力最高，轴心处压力最低；沿着轴向，从入口到底流口逐渐降低，负压区出现在强制涡区域(中心区域)。2个旋流器的静压梯度沿径向比沿轴向大很多。新方法旋流器的静压峰值更大，且径向梯度更大，更利于分离。

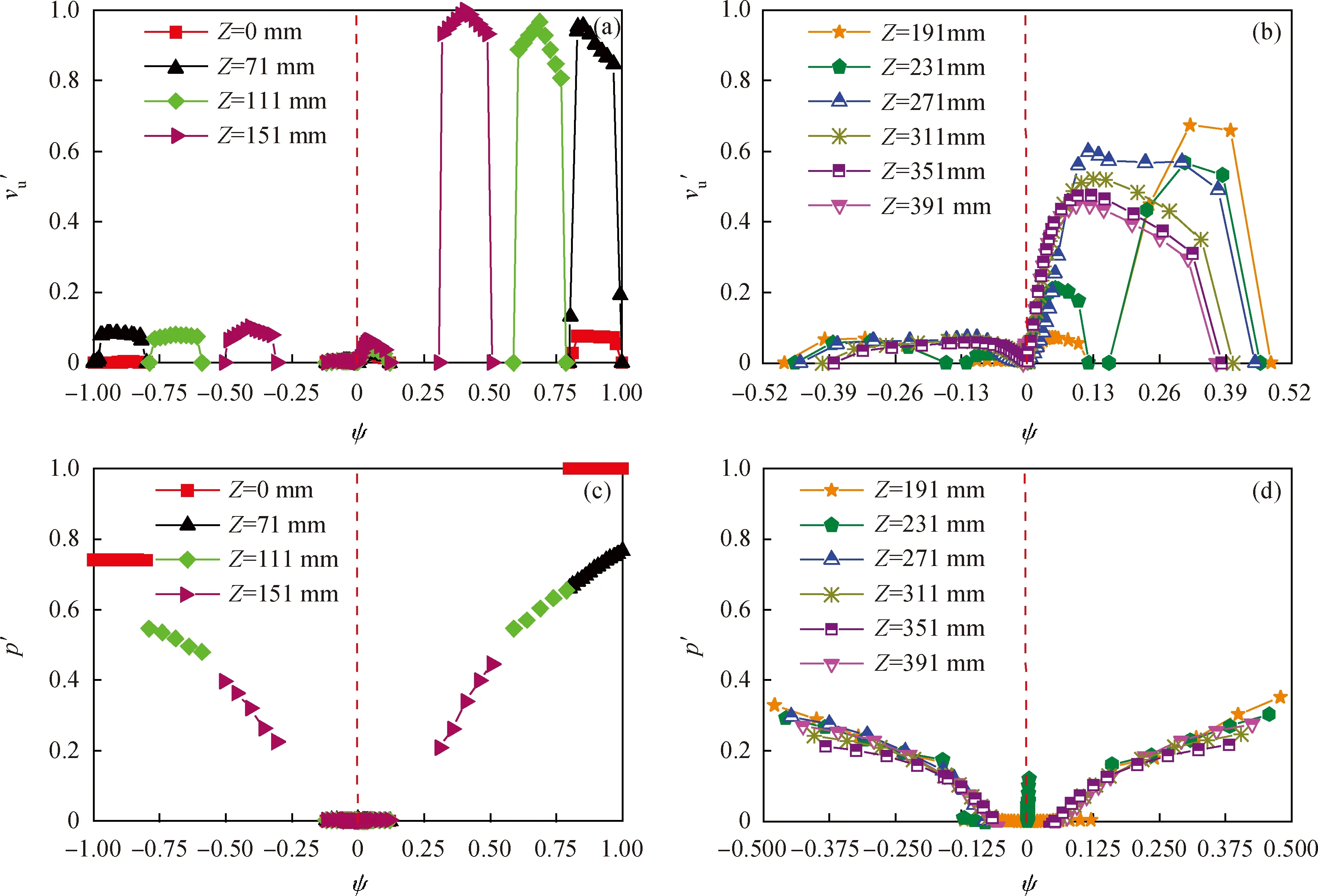
图9 2种设计方法导叶的切向速度和静压(p′)对比Fig.9 Tangential velocities and static pressures (p′) of guide vanes designed with two design methods(a) Tangential velocities in the sections of guide vane and large cone; (b) Tangential velocities in the sections of small cone;(c) Static pressures in the sections of guide vane and large cone; (d) Static pressures in the sections of small cone; The curves in the left side of red dotted line represent the physical parameter distributions of geometrical method guide vanes, and the curves in the right side of red dotted line represent the physical parameter distributions of the new method guide vanes.

为了进一步了解流场特性，分析对比了导叶末端Z=81mm处X、Y轴截面的合速度的云图，如图10所示。由图10可知，新方法的导叶加速能力明显高于几何法，且几何法旋流器的吸力边附近流体的速度很低，说明吸力边附近的流体并没有跟随主流旋转加速运动，产生了脱流，使导叶的效率下降。

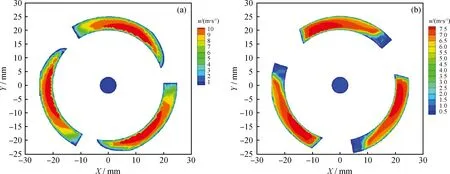
图10 2种导叶结构的旋流器速度(u)云图Fig.10 Velocity (u) contours of two guide vane cyclones(a) Guide vane designed with geometric method；(b) Guide vane designed with the new method

旋流器的压力降是衡量其能量损失大小的重要参数，常作为旋流器工作效率的重要指标。新方法在溢流口和底流口的轴向压力降与入口总压力的百分比分别为99.77%和99.21%；几何法在溢流口和底流口的轴向压力降与入口总压力的百分比分别为99.79%和99.60%。新方法的轴向压力降在底流口和溢流口都低于几何法，说明新方法旋流器的能耗略低。

液-液旋流器中，轻相液滴受到流体剪切后易破碎为更小的液滴，从而降低了分离效率，这种剪切与湍流强度关系较大，应该进一步研究。图11为2种导叶在X=0截面湍流强度云图。从图11可知，湍流强度分布规律相似，沿径向呈鞍形[22]，从器壁到轴心先增大再降低，沿轴向，从入口到底流口整体呈现先增加再降低。虽然湍流强度的分布规律相似，但数值上新方法的旋流器明显低于几何法，这说明了新方法的旋流器的流场各向异性更弱，流动更有规律，液滴破碎的概率更小。

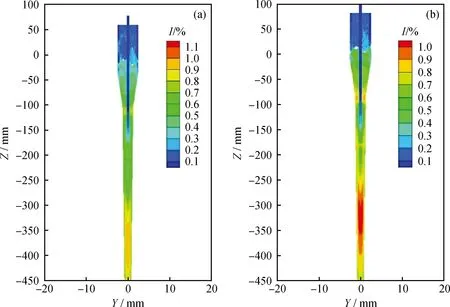
图11 2种旋流器在X=0截面上湍流强度(I)云图Fig.11 Contours of turbulent intensities (I) in two guide vane cyclones(a) Geometric method；(b) The new method

5 结 论

(1)笔者首次提出一种新的旋流器导叶结构的设计方法，采用Bezier曲线方程建立了导叶截面型线的参数化模型，并结合Matlab与Solidworks，便于快速造型设计导叶，可供工程设计使用。

(2)笔者提出的设计方法曲率连续且光滑性好，具有良好的形状控制能力，可以快速地调整设计参数，有利于准确、快速地设计优化双锥式液-液旋流器的导叶结构。

(3)模拟结果表明，新方法的切向速度较大，导叶对流体的加速能力和控制性更好，分离能力更高；压力降更小，能耗更低；湍流场各向异性较弱，液滴破碎的概率更小；因此新方法导叶更易于实现液-液分离。

[1] 刘培启，吴柯含，周运志，等. 一种双叶轮动态旋流分离器的压力性能[J].石油学报(石油加工), 2017, 33(4): 693-700.(LIU Peiqi, WU Kehan, ZHOU Yunzhi, et al. Pressure performance of double-impeller dynamic hydrocyclone[J].Acta Petrolei Sinica (Petroleum Processing Section),2017,33(4): 693-700.)

[2] 毛羽，时铭显． 导叶式旋风子叶片的设计与计算[J]．华东石油学院学报(自然科学版)，1983，(3): 306-318．(MAO Yu, SHI Mingxian. Guide vane design and calculation of axial flow cyclone[J].Journal of China University of Petroleum (Edition of Natural Science), 1983, (3): 306-318.)

[3] 张荣克，廖仲武． 多管第三级旋分器导向叶片参数的计算[J]．石油化工设备，1987，16(3): 17-22．(ZHANG Rongke, LIAO Zhongwu. The calculation of guide vane parameters in multi-tube third-level cyclone separator[J].Petro-chemical Equipment, 1987, 16(3): 17-22.)

[4] 金有海, 范超，毛羽，等． 导叶式旋风管叶片参数设计方法的研究[J]．化工机械, 1999, 26(1): 21-24. (JIN Youhai, FAN Chao, MAO Yu, et al. Study on the design methods of vane parameters of vane-guided cyclone tubes[J].Chemical Engineering & Machinery, 1999, 26(1): 21-24.)

[5] DIRKZWAGER M. A New Axial Cyclone Design for Fluid-Fluid Separation[M].Delft: Delft University of Technology, 1996.

[6] van CAMPEN L. Bulk Dynamics of Droplets in Liquid-Liquid Axial Cyclones[M].Delft: Delft University of Technology, 2014.

[7] van CAMPEN L, MUDDE R F, SLOT J,et al. A numerical and experimental survey of a liquid-liquid axial cyclone[J].International Journal of Chemical Reactor Engineering, 2012, 10(1): 1205-1224.

[8] SLOT J J.Development of a Centrifugal in-Line Separator for Oil-Water Flows[M].Enschede: University of Twente, 2013.

[9] WANG Z B, MA Y, JIN Y H. Simulation and experiment of flow field in axial-flow hydrocyclone[J].Chemical Engineering Research & Design, 2011, 89(6): 603-610.

[10] 钟芳源． 燃气轮机设计基础[M]．北京：机械工业出版社，1987: 202-208．

[11] 阿洛诺夫 Б М． 航空燃气涡轮叶片的造型[M]．北京：国防工业出版社，1980: 153-161．

[12] 马洪波，朱剑，席平． 基于参数化的涡轮叶片三维气动优化仿真[J]．计算机仿真，2008，25(10)：27-30．(MA Hongbo, ZHU Jian, XI Ping. Aerodynamic 3D optimization simulation of turbine blade based on parametric design[J].Computer Simulation, 2008, 25(10): 27-30.)

[13] 刘小民，张文斌． 采用遗传算法的离心叶轮多目标自动优化设计[J]．西安交通大学学报，2010，44(1)：31-35．(LIU Xiaomin, ZHANG Wenbin. Multi-objective automatic optimization design of centrifugal impeller based on genetic algorithm[J].Journal of Xi`an Jiaotong University, 2010, 44(1): 31-35.)

[14] 刘润泽，张晓东，安柏涛，等． 非均匀有理B样条曲线及节点插入算法在透平叶片优化设计中的应用[J]．航空动力学报，2010，25(2)：451-458．(LIU Runze, ZHANG Xiaodong, AN Botao, et al. Application of non-uniform rational B-spline curve and knot insertion algorithm to turbine blade optimization[J].Journal of Aerospace Power, 2010, 25(2): 451-458.)

[15] 高行山，韩永志，张娟，等． 基于近似技术的涡轮叶片气动优化设计[J]．计算力学学报，2008，25(6)：874-877．(GAO Xingshan, HAN Yongzhi, ZHANG Juan, et al. Blade aerodymic optimization design based on approximation method[J].Chinese Journal of Computational Mechanics, 2008, 25(6): 874-877.)

[16] 马文生． 多级轴流压气机气动优化设计研究[D]．北京：清华大学，2009．

[17] 周卫东，王瑞和，沈忠厚，等． Bezier 曲线在井底增压钻井离心泵叶片三维造型中的应用[J]．钻采工艺，2008，31(3)：84-86．(ZHOU Weidong, WANG Ruihe, SHEN Zhonghou, et al. Application of Bezier curve on the 3-D blade profiling of bottom hole intensifier centrifugal pump[J].Drilling and Production Technology, 2008, 31(3): 84-86.)

[18] 周卫东，李罗鹏，王瑞和，等． 高速多级离心泵叶片参数化造型设计[J] ．石油机械, 2008，36(5)：26-28. (ZHOU Weidong, LI Luopeng, WANG Ruihe, et al. Parameterized design of high speed multistage centrifugal pump blade[J].China Petroleum Machinery, 2008, 36(5): 26-28.)

[19] 彭茂林，杨自春，曹跃云，等．基于贝赛尔曲线和粒子群算法的涡轮叶片型线参数化建模[J]．中国电机工程学报，2012，32(32)：101-108．(PENG Maolin, YANG Zichun, CAO Yueyun, et al. Parameter modeling of turbine blade model line construction based on Bezier curve and particle swarm optimization algorithm[J].Proceedings of the CSEE, 2012, 32(32): 101-108.)

[20] AMARI S, CICHOCKI A. Adaptive blind signal processing-neural network approaches[J].Proceedings of the IEEE, 1998, 86(10): 2026-2048.

[21] 陈宝平，尹志凌． 基于有理二次Bezier曲线的G2连续的插值曲线[J]．内蒙古大学学报(自然科学版)，2004，35(4)：464-466．(CHEN Baoping, YIN Zhiling. An interpolating G2continuous closed curve based on rational quadric bezier curves[J].Journal of Inner Mongolia University (Edition of Natural Science), 2004, 35(4): 464-466.)

[22] 蔡香丽, 杨智勇, 马玉苗, 等. 旋风分离器内旋转流湍流特性的实验分析[J].石油学报(石油加工), 2015, 31(4): 983-990. (CAI Xiangli, YANG Zhiyong, MA Yumiao, et al. Experimental analysis of turbulence characteristics of swirling flow in cyclone[J].Acta Petrolei Sinica (Petroleum Processing Section), 2015, 31(4): 983-990.)