三款动态数学软件设计“迭代”类积件的比较分析*——以《圆的面积》公式推导为例

☆ 杨秀燕 黄立春 唐剑岚

（广西师范大学数学与统计学院，广西桂林 541004）

迭代是一种类似于程序设计中递归算法的特殊变换，是指按照一定的变换规则，由原象（发生迭代的初始对象）到初象（原象经过一系列变换操作得来的对象）反复映射的过程。原象可以是进行几何迭代的点，也可以是进行数值迭代的参数。

一、积件基本原理及效果

《圆的面积》是人教版六年级上册第五章的内容，在圆的面积公式的推导中渗透“转化思想”、“图形的割补”、“化曲为直”、“无限逼近”等数学思想与方法，有助于发展学生的空间观念和推理能力。

引入动态数学软件一方面是为了增强课堂互动性，另一方面旨在通过积件，动态视觉化的呈现圆切割并拼接成矩形的过程，从而突破圆的面积公式推导的难点，提效课堂教学。积件首先呈现半径为r且切割成若干等份的圆（如图1）；接着，将上、下部分扇形展开至同一水平线并拼接成矩形（或平行四边形），其中矩形的高近似圆的半径r，底近似圆周长的一半；最后，增加分割份数，得出矩形面积，从而推出圆的面积计算公式。

图1 圆的面积积件展示

一般而言，考虑将上、下半圆分成N等分，总体上为2N等分。N为奇数或偶数影响制作过程。首先，考虑当N为偶数时。在圆展开至同一水平线过程中，可以发现，各扇形上的弦与水平方向夹角逐渐减小，直至水平时夹角为0度。考虑四分之一圆（如图2），圆弧展开动画实质上经历了（1）Rotate({S4},P4,α)（表示扇形S4绕着点P4旋转α，α＞0时逆时针方向旋转）；（2）Rotate({S3,S4},P3,α)；（3）Rotate({S2,S3,S4},P2,α)；（4）Rotate({S1,S2,S3,S4},P1,α/2)。 其中α为等分后扇形的圆心角，值为180°/N，值得注意的是，弦P1P2在半径OP1上的弦切角仅为扇形所对的圆心角的一半。因此，上述（4）的旋转角为α/2。

图2 N为偶数

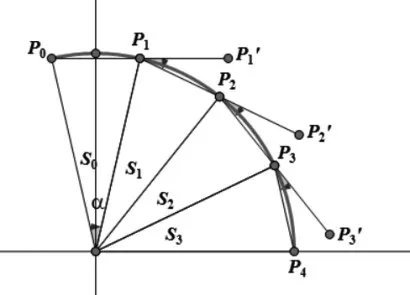
图3 N为奇数

由上分析可得，对四分之一圆n等分，展开动画为

接着，分析当N为奇数时。在四分之一圆中（如图3），发 生（1）Rotate({S3},P3,α)；（2）Rotate({S2,S3},P2,α)；（3）Rotate({S1,S2,S3},P1,α)。与N为偶数的区别在于不存在旋转角为α/2的情况。如下以N为偶数为例，分别应用三款软件实现圆的分割。

二、三款软件的制作过程

三款软件均能够动态地展现出几何对象的位置关系、运行变化规律。但是，操作过程与动画原理之间存在一定的差异性。

（一）几何画板制作过程

20世纪80年代几何画板由美国Key Curriculum Press公司制作并出版，1996年该公司授权人民教育出版社在中国发行该软件的中文版。强大的迭代功能是几何画板制作本积件的优势所在，特别是能够支持参数与几何的同步迭代，为本积件的制作带来了便利。具体制作过程如下。

1.创建控制点以及参数

绘制点A(1,0)与B(1,-1)，选中点O（原点）、A、B构造“三角形的内部”，并在三角形上取“边界上的点”，得点C，作为控制点；度量点C的横与纵坐标，新建参数t=1与 N=4；依次计算“abs(yc)”、“t=1”、“N-1”、“-90°/N”、“-90°/2N”、“90°(sgn(t-1)+1)/2/N·xc”。

2.确定半径以及制作拼接动画

在y轴上取点D，双击O标记中心，按固定比1/2缩放D得到点E；以O为中心，“-90°/2N”为旋转角，旋转E得到点E′；以D为中心，缩放E′固定比-yc/2得到点F；标记向量DO，平移F得到点F′。其中点D用于控制圆的半径大小。

3.制作迭代原像

在画布上任意画G、H两点，以G为中心，最后一个参数为旋转角度（如图4），旋转H得到点H′；再以H′为中心，“-90°/N”为旋转角，旋转G得到点 G′；连接线段FF′，双击线段FF′标记镜面，反射如图5所示扇形（包括线段GH′、G′H′、弧 GG′以及面 GG′H′）；再以O为中心，将两扇形旋转180°。

图4 几何画板各参数

图5 迭代原像

4.深度迭代

依次选中G、H、t以及N-1，按住Shift键不放，选择深度迭代，创建 (G,H,t)→(G′,H′,t+1)的迭代；选中点G和F，单击“编辑/合并”，重复操作，将点H和F′也合并。

5.优化界面

隐藏无关对象，分别制作C到A、B、O的移动按钮，添加文本等。此时已实现“化圆为方”效果，其中底边长为周长的一半πr，高为半径r。

（二）Hawgent皓骏制作过程

Hawgent皓骏是一款动态数学软件，能够处理几何、代数、三角、概率、统计、算法、微积分等数学问题，并且能够根据图形间的逻辑关系推理出几何性质，即自助推理。Hawgent皓骏同样具备迭代功能，虽然当前版本不能实现参数与几何图形的同步迭代（数值迭代中的参数能在几何迭代中直接应用），在本案例中无法判断旋转角为α还是α/2，但也可以通过其他操作达到目的。其具体实现方法如下。

在此之前，有必要说明：Hawgent皓骏测量值或计算值按照创建顺序默认给参数赋予u000-u999形式的变量名，引用参数时只需手动输入参数的变量名即可。

1.创建控制点以及参数

显示坐标系，绘制点A（0，0）、B（1，0）、C（1，-1）；依次选中A、B、C创建多边形，在多边形上取点D；测量D的X-坐标XD与y-坐标yD，此时XD、yD变量名分别为u000、u001；创建变量尺，其中变量名为n，范围为2到10，计算“ -90/floor(n)”。

2.确定半径并制作拼接动画

在y轴上取点E，依次选中A、E，创建中点F；依次选中F、A，构造旋转变化旋转“u002/2”得到点G；依次选中E、G，创建参数为“-u001”的参数点H；依次选中H、E、A，构造平移变换得到点I，线段连接HI。

3.制作迭代原像与初像

依次选中I、H，构造旋转变换旋转“-u000*u002/2”得到点J；依次选中H、J，构造旋转变换旋转“u002”得到点K；依次选中点H、J，绘制指定圆心角的圆弧，其中圆心角为“u002 ”；连接线段HJ、KJ；重复上述操作，J绕 K旋转“-u000*u002”得到点L，然后K绕L旋转“u002”得到点M，创建圆弧连接线段。

4.迭代变换

依次选中J、K，单击迭代打开迭代窗口，新建(J，K)→(L,M)映射，勾选显示弧以及扇形的两条边，确定迭代。此时默认做5次，激活编辑模式，在对象窗口中找到迭代，右键打开迭代属性窗口，修改迭代层数为“floor(n)-2”。

5.完善图形优化界面

选中所有扇形以及线段HI，构造对称变换；再次选中所有扇形以及点A，构造旋转变换旋转180°；选中点D创建变量尺，隐藏无关变量，填充扇形颜色等（如图6）。

图6 Hawgent皓骏

（三）玲珑画板制作过程

经过多年的探索与更新，玲珑画板在平面几何、立体几何、解析几何、不等式、函数等领域应用广泛。特别是在立体几何上有着不错的表现，立体图形的创建、空间动画制作等均有所突破。遗憾的是，玲珑画板当前版本缺失迭代功能。所以在本案例中，只能制作确定切割份数的积件，具体制作过程如下。

1.等分圆以及创建参数

右键选择“2D网格模式”，在网格上绘制半径为4且第二个点位于圆心的正右侧位置的圆，然后隐藏网格；自左向右用线段连接圆心与圆上的点，并在线段上取一点A；新建参数a，双击参数，选中线段上的点，修改终值为0.5，最大值为30，选中点A绑定动点。此时点A在0到0.5位置上移动时参数a的变化范围是0到30。

2.制作展开动画

将圆12等分，对点添加标签；单击“创建—变换—旋转”打开旋转变换窗口，首先以点P3为中心，旋转角度为a，将P4与O添加变换得到点O1和P5；然后再以P2为中心，旋转角度为a，将对P3、O以及O1、P5添加变换得到点 O2、O3、P6、P7；最后再以P1为中心，旋转a/2角度，将P2、O、O2、O3、P6、P7添加变换得到点 O4、O5、O6、P8、P9、P10。由于过程中涉及的点过多，可选择性的将不需要的点隐藏。

3.补充其余展开动画

连接OP1并作其中点B，选中点B，以O旋转中心，旋转角度为-15°，添加变换得到点B′；连接OB′，在O点上新建自由点O′；打开平移动画窗口，选中点A设定变量（拖动A可以实现动画过程），选中OB′设定平移轴，修改起值为0.5终值为1，将O′添加到动画；以OP1为旋转轴，旋转角度为180°，对各扇形上的点添加变换；最后再以O′为中心，旋转角度为180°，对各扇形上的点添加变换。如此即可补充其余部分圆上的展开动画。

4.优化界面

将各扇形圆弧补充完整，并创建“圆弧面”；修改颜色，隐藏无关对象等（如图7）。

图7 玲珑画板

三、总结与思考

Hawgent皓骏与玲珑画板是国内新兴的动态数学软件，较之几何画板或许不够成熟，但也各具千秋。对比发现，几何画板的迭代功能较强，能支持几何与数值的同步迭代。而Hawgent皓骏的几何迭代与数值迭代虽然分开进行，但也能实现较好的迭代功能。玲珑画板目前还不能很好的支持迭代，于本案例而言，几何画板更具优势。

在实际教学中，教师可根据教学需求选择合适的软件。当然，技术的使用是手段而不是目的。如果使用得当，将技术有机融入数学教学中，帮助学生理解数学，提高学生的学习兴趣，改善学习方式，将能在“授人以鱼”的同时“授人以渔与欲”。

[1]唐剑岚等主编.计算机辅助数学教学原理与实践[M].北京：清华大学出版社,2012.

[2]唐剑岚,庄丽薇.优化圆的面积公式推导的课件设计[J].中小学电教,2011(10):64-66.

[3]张景中,彭翕成.三款数学教育软件的比较与设计思想分析[J].中国电化教育，2010(01):107-113.

[4]张景中,彭翕成.函数作图软件的评价和选择[J].数学通报,2007(08):1-9.

[5]唐剑岚.鱼渔欲”三位一体优化数学教学的理念与策略—以“三角形的内角”课例片段分析为例[J].基础教育研究,2015(09):5-10.

[6]唐剑岚,周元.授人以鱼”的同时“授人以渔与欲”—以《等差数列的前n项和》公式推导片段为例[J].数学通报,2016(09):41-46.